带有交叉感染的狂犬病模型及其控制策略研究
许传青,韩笑颖,崔景安*,纪振伟,徐大舜
(1.北京建筑大学 理学院,北京 102616;2.南伊里诺伊大学 数学系,卡本代尔 62901,美国)
狂犬病是由狂犬病病毒引起的一种人畜共患的中枢神经系统急性传染病,多见于犬、狼、猫等肉食动物,人多因被病兽咬伤而感染,临床表现为特有的恐水、怕风、咽肌痉挛、进行性瘫痪等症状.目前尚缺乏对狂犬病有效的治疗手段,一旦被感染,死亡率几乎为100%,是迄今为止人类病死率最高的急性传染病[1].自1996年的158例到2007年的3 300例,中国狂犬病发病人数处于持续增长状态.尽管从2008年开始狂犬病发病人数略有下降,但离2020年达到控制狂犬病的目标,我国仍面临着巨大挑战,如图1所示.随着我国国际地位的不断提高,在医疗卫生的各个方面都应该彰显出大国的影响力,因此对狂犬病的控制问题是当前需要重视的重大传染病问题.
数学模型可以在传染病动力学模型中对一些控制策略做出有效指导.Zhang等[2]建立了中国狂犬病传播的数学模型,并通过数值模拟说明对家犬进行免疫对控制狂犬病有重要作用.Chen等[3]研究了狂犬病跨地区传播的方式,讨论了地区之间的传播对基本再生数的影响,即为了防止狂犬病地区之间的传播,应该规范狗的市场管理,在运输犬只的过程中要不断地监控检测.Hou等[4]以广东省为例,研究了家犬在成为野犬过程中的传播机制,说明了对家犬管理的重要作用.文献[5-6]从统计学角度建立模型对狂犬病的发病情况进行短期预测,应用乘积季节模型和应用趋势季节模型对近几年的人类狂犬病病例数据进行分析拟合,来判断下一年人类狂犬病病例的走势情况.在其他狂犬病动力学模型中,部分学者在模型中对狂犬病控制采取疫苗接种和捕杀等措施[7-8],并比较了这些控制策略对狂犬病传播的有效性[2],多数学者赞同免疫是目前最好的控制策略.
目前中国的野犬数量庞大并且食物相对充足,学校、工厂、垃圾堆成为野犬生活的主要聚集地,它们的繁殖受到的控制措施有限.论文结合狂犬病的传播机制,建立了野犬、家犬、人类3个群体相互作用的狂犬病模型,并通过遗传算法对数据与模型中的染病人数进行拟合,预测了我国狂犬病人数未来30年的走势情况,估出了当前控制策略下我国狂犬病的基本再生数R0≈1.075,最后通过调节影响基本再生数相关参数的大小,说明综合控制策略对控制狂犬病蔓延的重要作用.
1 数学模型
考虑野犬、家犬和人3个群体间的模型,其中野犬、家犬和人都被分为4个仓室.S1,E1,I1,R1和S2,E2,I2,R2分别表示野犬、家犬中的易感者、潜伏者、感染者和接种恢复者;Sh,Eh,Ih,Rh表示人中的易感者、潜伏者、感染者和接种恢复者.数学模型如下所示:
犬类
(1)
人类
(2)
模型中的参数均为正数.对于犬中的群体:A1,A2表示野犬和家犬每年的平均出生数;p1,p2表示潜伏期的野犬和家犬没有爆发狂犬病现象又恢复到易感者里的比率;β1S1I1,β′1S1I2表示单位时间内染病的野犬和家犬对易感野犬的传染数;β2S2I2,β′2S2I1表示单位时间内染病的家犬和野犬对易感家犬的传染数;γ1,γ2表示野犬和家犬的免疫率;c1,c′1表示普通野犬和免疫野犬的捕杀率;μ1,μ2表示野犬和家犬的自然死亡率;σ1,σ2表示潜伏期野犬和家犬到染病期的移出率;l1表示免疫野犬的领养率;α1和α2表示野犬和家犬的因病死亡率;λ表示家犬接种疫苗的失效率.对于人的群体:H表示人每年的平均出生数;ph表示潜伏期的人群没有爆发狂犬病现象又恢复到易感者人群的比率;λh表示人群里接种疫苗的失效率;βhShI1,β′hShI2表示单位时间内染病的野犬和家犬对易感人类的传染数;γh分别表示人群中的免疫率;m表示人群的自然死亡率;σh表示潜伏期的人群到染病期的移出率;αh表示人群的因病死亡率. 狂犬病模型流程如图2所示.
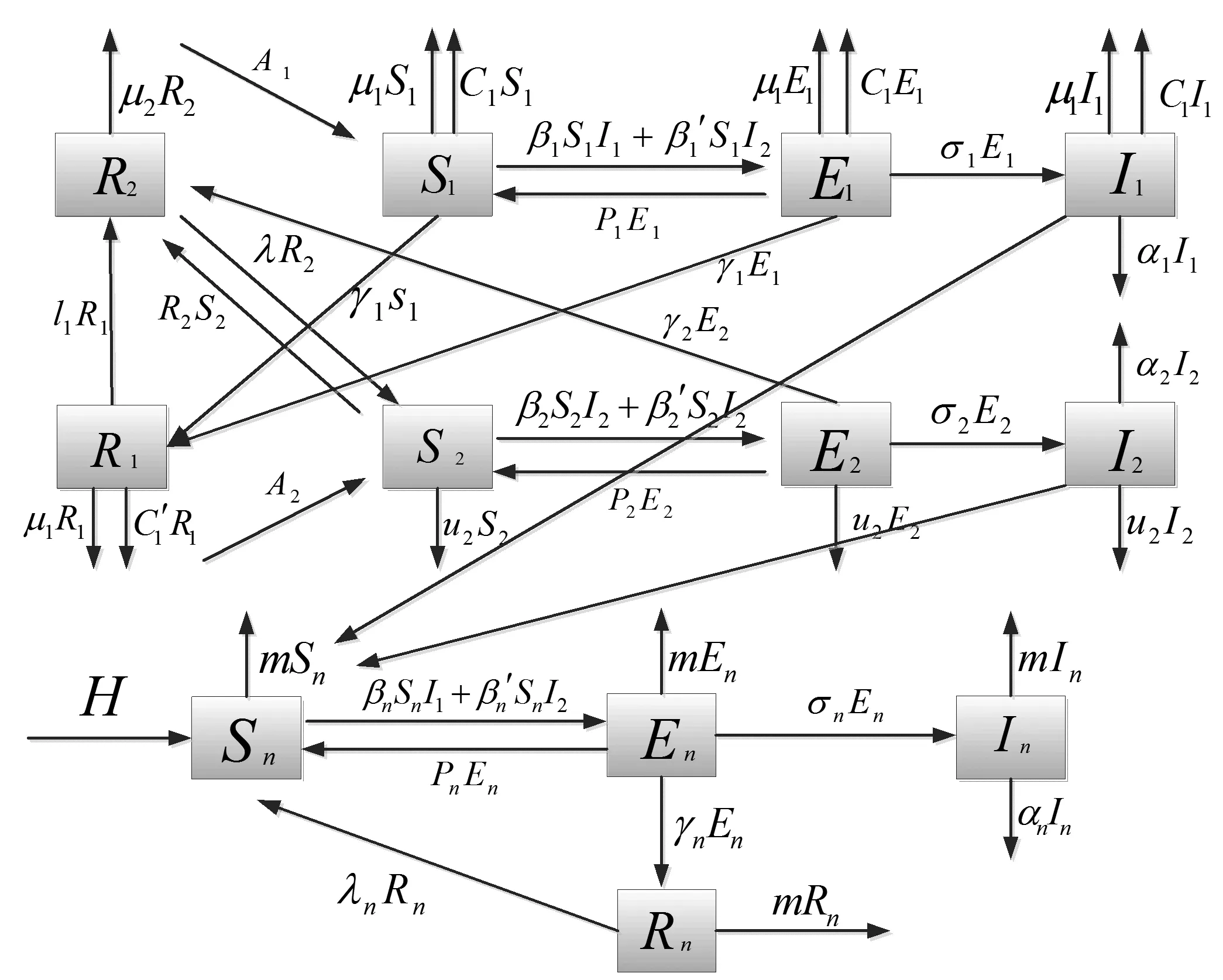
图2 狂犬病在野犬、家犬与人中的染病流程
2 平衡点以及基本再生数的计算
从模型(1)中得到
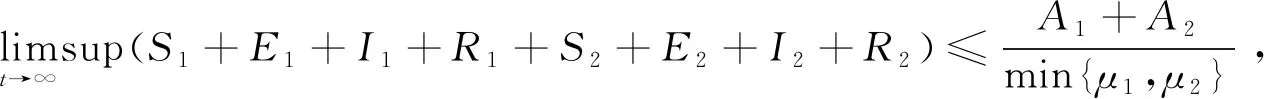
基本再生数考虑如下辅助系统
(3)
由文献[9]中计算基本再生数的方法得到
因此再生矩阵为
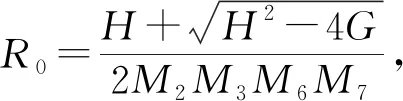
可以发现
3 无病平衡点全局稳定性分析及模型的一致持续性
定理1R0<1时,无病平衡点是全局渐近稳定的.
证明令M=F-V,定义s(M)=max{Reλ:λ是M的特征值}[10].根据文献[9]中的定理2,存在两个等价关系
R0>1⟺s(M)>0,
R0<1⟺s(M)<0.
为了得到无病平衡点的局部稳定性,需要符合文献[9]定理中的5个条件.前4个条件显然成立,对于第5个条件,只需满足下面这个8×8阶矩阵的特征值全部为负
其中
计算J4的特征值有
s(J4)=max{-M1,-M4,-μ2,-(γ2+λ+μ2)}<0.
当R0<1时,可以得到s(M)<0,因此s(J|P0)<0,即模型(2)的无病平衡点是局部渐近稳定的.
由模型(2),有以下方程成立
A1-(μ1+c1+γ1)(S1+E1),
得到
由于E1≥0,E2≥0,故
对于模型(2),有
得到
由模型(3)可知
则存在一个t0,当t>t0时,考虑相关的线性系统
(4)

定理2R0>1时,疾病是一致持续生存的.
证明令Φt(x)=Φt(t,x(t))是可行域X上的连续流,x(t)是模型(1)关于初值
x(0)=(S1(0),E1(0),I1(0),R1(0),S2(0),E2(0),I2(0),R2(0))∈X
的解.其中X0={(S1,E1,I1,R1,S2,E2,I2,R2)∈X|E1,I1,E2,I2>0};∂X=X|X0,∂X是可行域X上的边界;Ω是Φt(x)在∂X上的最大不变集.可以得出下面的结论:当R0>1时,对于初值S1(0),R1(0),S2(0),R2(0)>0,且E1(0),I1(0)>0或E2(0),I2(0)>0的任意解x(t),Φt(x)在可行域X上是一致持续的.
当R0>1时,模型(1)存在正解. 对于模型(1)的任意解x(t)在E0充分小的临域内,分成两种情况讨论:
(1) 如果I1(0)=E1(0)=I2(0)=E2(0)=0,则I1(0)=E1(0)=I2(0)=E2(0)≡0.模型(1)表示当t→-∞时,(Si(t),Ri(t)),i=1,2远离P0.
(2) 如果E1(0),I1(0)>0或E2(0),I2(0)>0,则对于任意的t>0,E1(t),I1(t)≥0或E2(t),I2(t)≥0.当x(t)充分接近P0时,对于模型(1)存在一个ρ,使得
(5)
其中:a11=-M2-ρ,a12=β1S1-ρ,a14=β′1S1-ρ,a21=σ1-ρ,a22=-M3-ρ,a32=β′2S2-ρ,a33=-M6-ρ,a34=β2S2-ρ,a43=σ2-ρ,a44=-M7-ρ.
当R0>1时,s(M)>0,模型(5)的最大特征值是正的,这个模型的线性近似系统为
因此当t→∞时,(x1(t),y1(t),x2(t),y2(t))→(∞,∞,∞,∞).根据比较原则[10],(E1(t),I1(t),E2(t),I2(t))→(∞,∞,∞,∞).由于P0关于模型(2)是全局渐近稳定的,显然P0是Ω上的唯一的平衡点,得到P0在X上是个孤立的点.Ω上的每条轨线收敛于P0,则P0是Ω上的非循环覆盖.根据Freedman一致持续准则[11],当R0>1时,得到模型(1)是一致持续的.
4 参数估计及数值模拟
由于我国还没有建立狂犬病学检测数据库,因此模型中的一些参数只能根据一些文献及报道进行估计.狂犬病的真实数据来自我国公共卫生科学数据中心、国家卫生健康委员会公报,其他具体参数见表1.
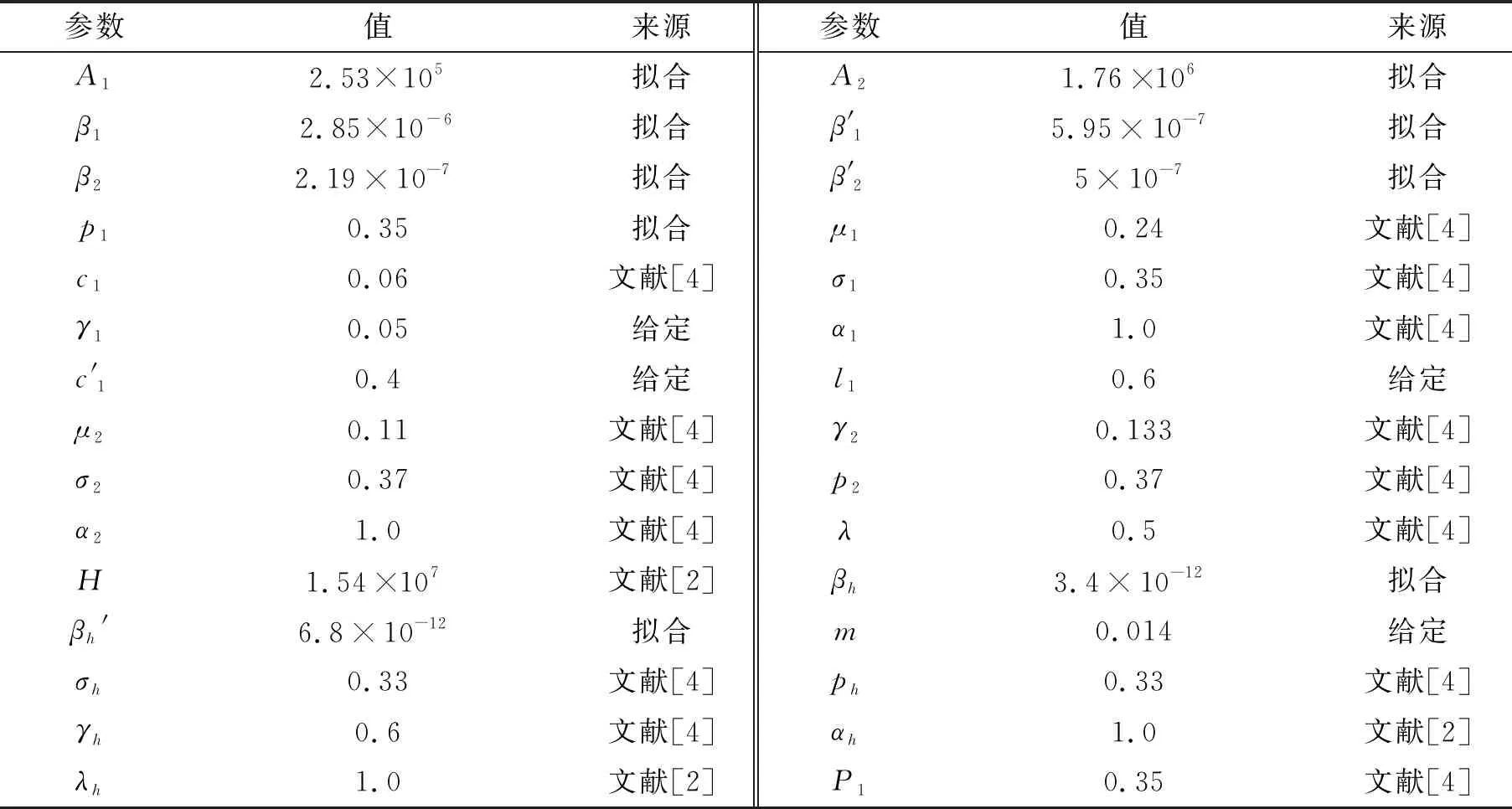
表1 数值模拟中用到的参数值
利用遗传算法拟合我国1996-2015年狂犬病染病数据,见图3.各个量的初值分别为
S1(0)=2×106,E1(0)=7×104,I1(0)=2×104,R1(0)=1×105,Ih(0)=158,Rh(0)=2×105,
S2(0)=3×107,E2(0)=2×105,I2(0)=5×104,R2(0)=5×106,Sh(0)=1.29×109,Eh(0)=400.
染病人数的变化趋势见图4.从模拟结果可以观察到染病人数在10年左右达到一个峰值,峰值的大小在拟合过程中与实际稍有偏差,之后染病人数Ih开始逐年下降.在当前控制策略下,可以发现染病人数Ih会持续减少,狂犬病的染病人数依然处于下降趋势,大约在10年左右趋近于一种平稳的状态,保持在500人左右的水平.根据图像拟合,可以得到相关参数的大小.根据参数的值,计算得到此状态下的基本再生数R0≈1.075.
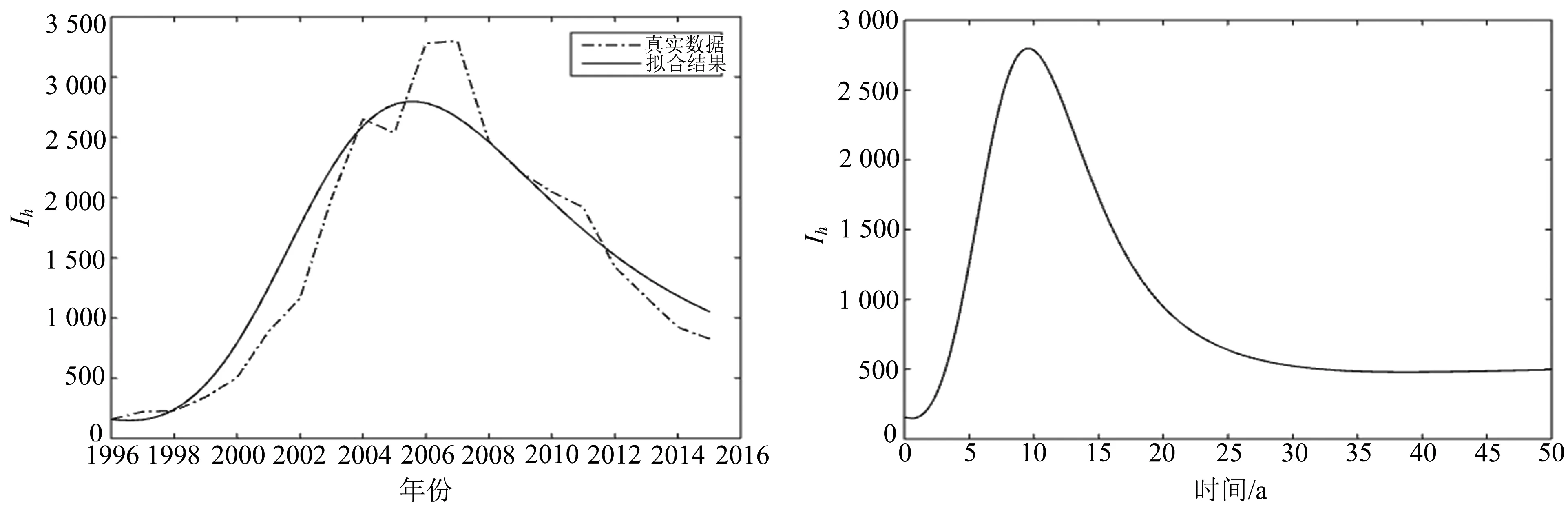
图3 真实数据与拟合图像 图4 染病人数50年的走势
首先考虑交叉感染对基本再生数和染病人数的影响,如图5(a)所示.避免家犬与野犬之间的交叉感染可以降低基本再生数R0的大小,如果家犬与野犬的接触率为零,看到R0可以降到1以下,这对狂犬病的控制尤为重要.图5(b)为交叉感染对染病人数走势的影响,可以看出避免家犬与野犬交叉感染能有效降低染病人数.
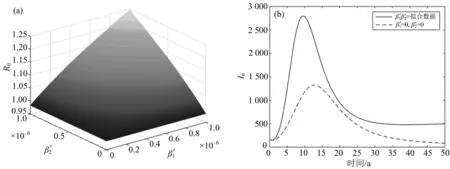
图5 R0及Ih关于β′1和β′2的图像
下面考虑家犬和野犬对基本再生数R0的影响.控制野犬的模拟结果见图6.
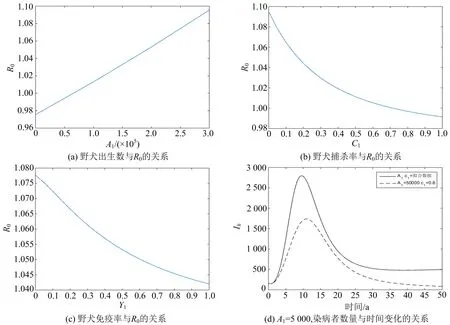
图6 R0及Ih关于控制野犬相关参数的图像
从图6可以看出,对于野犬而言增大捕杀率和减少野犬的出生数量可以使R0降到1以下,对野犬进行免疫处理虽然对R0的降低有一定的作用,但并不能使R0降到1以下.图6(d)是对野犬实行双重控制的效果,可以看到加大对野犬的管理力度对控制狂犬病的发生有着重要影响.在我国,家犬的数量要远远大于野犬的数量,重点要对家犬采取控制措施,结果见图7.由图7可知,控制家犬的出生数量和增大家犬的免疫率都可以使基本再生数R0降到1以下,但由于我国对犬只的需求量巨大,很难控制家犬的出生数量,因此增大家犬的免疫率是行之有效的控制措施.

图7 R0关于控制家犬相关参数的图像
5 结束语
鉴于狂犬病传播问题的严重性,建立数学模型来研究控制狂犬病的有效策略.通过拟合中国近20年来狂犬病患者的数据,找出野犬、家犬、人之间在传播疾病过程中最适合的接触率,从而得到基本再生数R0≈1.075.从对基本再生数的影响分析中得出控制狂犬病的策略:首先应该做好对家犬的管理,避免家犬与野犬之间的交叉感染;应加大野犬捕杀力度,在一些特殊保护的地区可以采取绝育的措施来控制野犬的出生数量;对于家犬而言,由于人类对犬只的需求量巨大,控制其出生数量可能存在一定的困难,但是对其进行免疫接种是行之有效的控制策略.我国野犬、家犬的数量很大,免疫率低,并缺乏有效应对犬类撕咬后的预防措施,这些都对狂犬病的控制有着不利的影响.在这种情况下,关键是要做好犬的管理和免疫,使得对家犬和野犬的控制策略得以实施,把我国狂犬病的控制水平提升到一个新的高度.尽管该模型为了便于分析忽略了一些随机的因素,但是通过模拟也发现了综合控制策略对控制狂犬病传播的重要作用,为我国狂犬病传播的控制提供了理论支持.

