摩托车皮带盘变形矫正研究

武君雯，张 涛*，杨洪涛，禹 斌

(1.安徽大学 电气工程与自动化学院，安徽 合肥 230031;2.安徽理工大学 机械工程学院，安徽 淮南 232001)

通过油门控制曲轴转速，无级变速系统(continuously variable transmission)能实现传动比连续变化，且不存在传动比突变造成的冲击，因此其广泛用于摩托车的传动系统.其核心是皮带传动的无级变速部件，当输入轴的转速较小时，输出轴不转；当输入轴加速至某一转速时，皮带张紧，输出轴开始转动；随后输入轴的转速增加时，输出轴的转速也逐渐增加，甚至高于输入轴的转速.无级变速动力传递机构主要由前传动和后传动两大部分组成.后带轮由固定盘、移动盘及弹簧组成.焊接和热处理后，固定盘及移动盘变形引起的跳动量可达0.8 mm，使皮带张力周期性变化，进而导致车身震动，影响行车的安全性及舒适性，因此必须对该变形进行矫正.人工矫正是目前广泛使用的方法，人工矫正完全依靠经验和感觉，若大批量生产，需要很多人工才能完成矫正，且效率低、一致性差，因此有必要进行自动矫正.提高自动矫正设备的矫正效率和矫正质量的关键是对摩托车皮带盘的矫正机理进行研究.笔者采用有限元仿真，分析皮带盘变形量与矫正量的关系，建立变形量与矫正量的关系模型，并基于模型进行实验验证.

1 矫正原理

通过测量仪器，确定零件需要矫正的区域，利用人工或者液压机械等施加外力，使零件发生弯曲、拉伸等变形，改变零件的弯曲曲率，使其达到平直.根据弹塑性理论[1-2]，零件会出现3种变形状态：弹性弯曲极限状态、弹塑性弯曲状态、全塑性弯曲状态.在第1种状态，零件弯曲变形并没有达到屈服极限，去掉外力后，零件恢复原状.在第2种状态，零件既发生弹性变形又发生塑性变形，去掉外力后，发生弹性变形的部分能恢复，而塑性变形部分则保留.第3种状态为理想情况，零件发生完全塑性变形.如何从理论上判断被矫正物体是否由弹性状态进入塑性状态，需要知道零件满足的屈服条件，且以这些条件为基础，建立零件的力学方程、几何方程、本构方程，进而确定需要施加的矫正力大小、每次矫正后的变形量大小和需要矫正的次数[3-6].

图1为摩托车皮带盘实物图，其外形为有一定锥度的圆盘.需矫正的位置随机分布于皮带盘，对某位置的矫正可能引起其他位置变形，从而增加矫正的次数，降低矫正效率.因此，笔者采用有限元仿真[7-9]研究摩托车皮带盘的受力变形及矫正机理.

图1 摩托车皮带盘实物图

2 摩托车皮带盘受力变形机理

2.1 有限元模型

按照实际零件尺寸建立皮带盘的3维模型，然后将其导入Ansys有限元分析软件，对皮带盘进行网格划分.根据皮带盘矫正设备的固定情况可知，边界条件为对皮带盘中心的6自由度约束.选GB699规范的15#钢为皮带盘材料， 根据边界条件及加载，可得零件内部任意点的应力、应变及位移等参数，以此分析皮带盘的变形情况.摩托车皮带盘材料为15#钢，双线性等向强化模型对该类钢有很好的近似，故采用双线性等向强化模型(bilinear isotropic hardening material model)进行仿真.图2为摩托车皮带盘塑性材料的特性曲线.由图2可知，当承受的应力超过屈服应力后，变形将进入塑性区.因此，可对皮带盘的特定位置施加外力，使需矫正的区域产生永久塑性变形，从而达到矫正的目的.

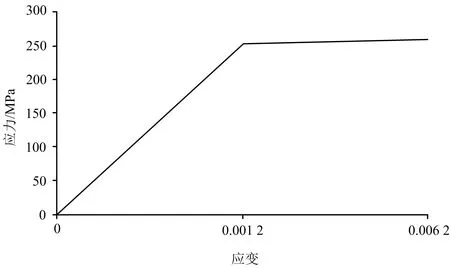
图2 摩托车皮带盘塑性材料的特性

2.2 矫正力与变形量的关系

皮带盘的平衡方程为

(1)

边界条件为

(2)

(3)

其中：a为皮带盘内径，b为皮带盘外径，P为矫正压力，ω(r,θ)为挠度函数.

采用如下的分离变量

ω(r,θ)=R(r)·Θ(θ)，

(4)

则有

(5)

单位长度的剪切力为

(6)

根据边界条件(3)，有

(7)

可得

(8)

(9)

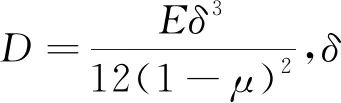
边界条件为

R(a)=0,R′(a)=0,R″(b)=0,

(10)

Θ(π)=0.

(11)

由(8)，(10),(11)式，解得

(12)

采用里兹法，设

Θ(θ)=c1cos2θ+c2cosθ+c3.

(13)

将(13)式代入(9)，(11)式，得

(14)

其中：c为待定参数.将(12),(14)式代入如下的系统应变能函数

(15)

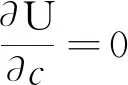
(16)

圆盘的挠度函数为

(17)

由(17)式，可得

(18)

环向最大弯曲正应力为

(19)

将皮带盘沿圆周等分为A，B，C，D区域.图3为力F作用下的皮带盘变形图.由图3可见，在力的作用下，皮带盘变形区域内既有弹性变形，也有塑性变形，红色区域的变形最大、蓝色最小.在压力F的作用下，A区域的变形量随力增大而增大.当A区域向下变形量达到1 mm时，B区域也出现向下的变形.在A区域的整个变形过程中，C区域和D区域均出现与A区域方向相反的变形.

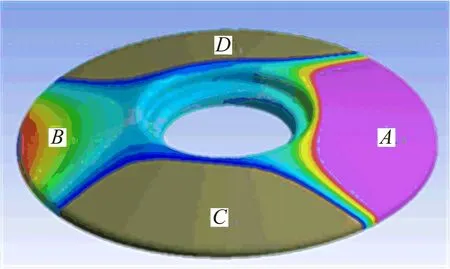
图3 力F作用下的皮带盘变形图

图4为力撤销后的皮带盘变形图，由图4可知，当外力F撤销后，A区域既有弹性变形也有塑性变形，当A区域的变形量达到1 mm时，力F撤销后A区域残留的变形量可达近0.1 mm，即产生了0.1 mm的矫正量.B，C，D区域大部分为弹性变形，力F撤销后这3个区域的变形量均在0.01 mm以内，因此可不考虑A区域矫正对B，C，D区域的影响，但要控制矫正力的临界值，防止在对A区域进行矫正的过程中，其他区域也发生较大的塑性变形，导致重复矫正，影响矫正的效率[10].

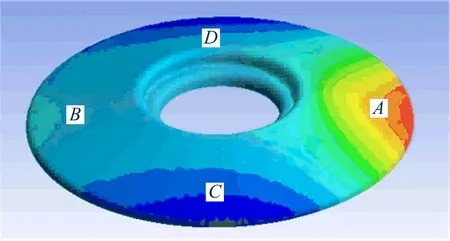
图4 力撤销后的皮带盘变形图

3 矫正试验

利用有限元仿真软件Ansys软件可得到不同矫正力作用下的皮带盘矫正量的理论值[11]，但在实际矫正过程中，皮带盘的矫正量还与矫正力施加的速度、矫正力作用点的位置等因素有关.笔者根据仿真实验结果，使用如图5所示的手动矫正设备进行实验.皮带盘通过中心孔固定在设备的芯轴上且可自由转动，皮带盘的变形量用百分表测量，矫正力由垂直于皮带盘上方的压头通过手轮旋转施加.

图5 实验装置

为了分析皮带盘下压变形量和矫正量之间的关系，选择不同的需矫正的皮带轮，通过手轮和压头对皮带盘施加矫正力，使其产生1.0，1.5，2.0 mm的下压变形量.在皮带盘同一位置连续3次施加1.0 mm下压变形量对应的矫正量如表1所示.

表1 在皮带盘同一位置连续3次施加1.0 mm下压变形量对应的矫正量

从表1可以看出，对同一位置连续3次施加相同的下压变形量进行矫正，第1次施压后出现了较大的矫正量,第2次的矫正量较小，第3次出现了反弹.可见，在同一位置连续施加矫正力产生的皮带盘塑性变形量会逐渐下降，甚至出现反弹.表2为不同下压变形量作用下的矫正量.从表2可以看出，不同下压变形量对应的矫正量不同，必须针对不同的变形量初始值选择合适的下压变形量，才能达到较高的矫正效率.

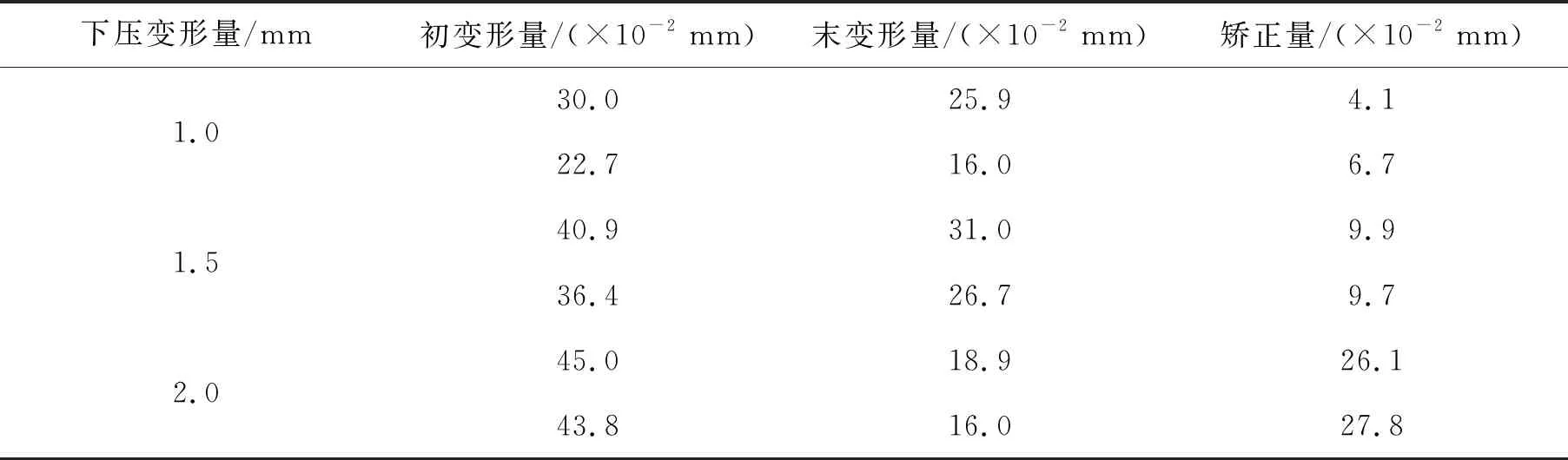
表2 不同下压变形量作用下的矫正量

选取一最大残余变形量为0.57 mm皮带盘，对圆周进行16等分，用2.0 mm的下压变形量对其施压矫正.矫正的过程[12]如下：确定皮带盘最大变形量所在位置，用手轮施加压力，使皮带盘产生2.0 mm下压变形量，保持5 s后松开手轮；再次确定皮带盘最大变形量所在位置，在此位置上应用2.0 mm下压变形量进行矫正.图6为皮带盘边沿圆周的矫正量，从图6可看出，在皮带盘某一位置进行矫正，会引起其他位置的微小变形，这与Ansys仿真软件分析的结果一致.用2.0 mm下压变形量进行8次矫正后，皮带盘边沿圆周的跳动量在0.15 mm之内，符合零件跳动量要求.

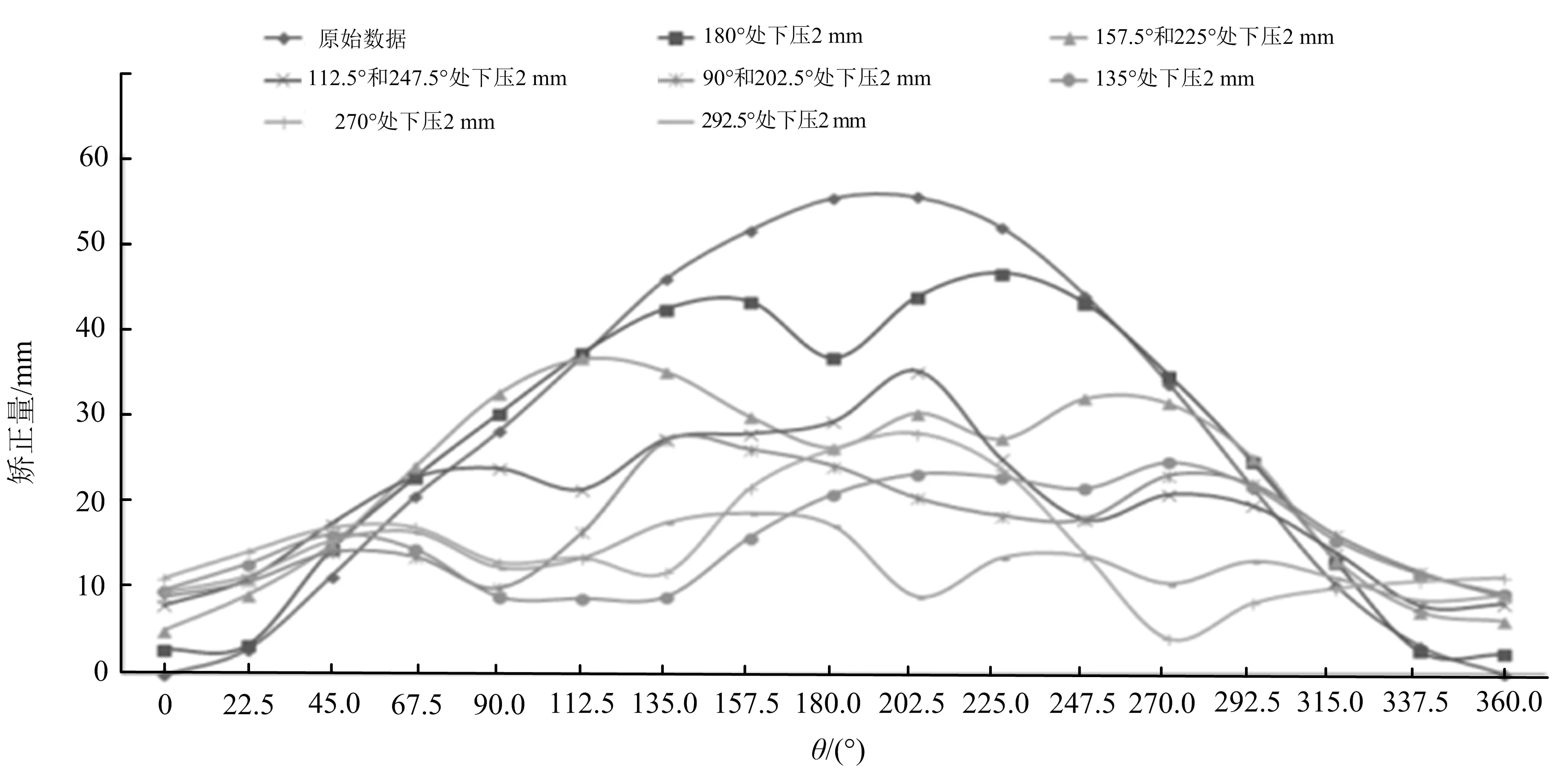
图6 皮带盘边沿圆周的矫正量

4 结束语

笔者通过有限元仿真，研究了皮带盘的受力弹塑性变形的机理，分析了矫正力大小、作用位置与该位置变形量间关系.根据仿真实验结果，对皮带盘进行了在不同矫正力作用下的矫正实验.实验结果表明，在同一位置连续施加矫正力产生的皮带盘塑性变形量会逐渐下降，不利于矫正，所以在矫正过程中，每次矫正前均必须确定皮带盘最大变形量的位置，在新的最大变形量处进行矫正，这样可以提高矫正效率.根据该文分析得到的变形量与矫正量关系模型，能有效实现皮带盘的矫正，且矫正效率高.该文的实验结论可指导后续的自动矫正设备的研发，以提供矫正的效率.