最大差值图决策的低照度图像自适应增强算法

王瑞尧，岳雪亭，周志青，耿则勋

（平顶山学院信息工程学院，河南平顶山467000）

（∗通信作者电子邮箱wry0304@126.com）

0 引言

视频监控图像设备广泛应用于公共安全、交通管理以及工业生产等许多领域，清晰的高质量图像可以为案件侦破、智能交通、安全生产提供强有力的帮助。而在实际获取图像过程中，往往会受到多种因素的干扰，尤其是在夜间低照度条件下。由于夜间微弱的环境照明、不均匀的曝光等原因，导致此时捕获到的图像往往整体灰度级水平较低，且场景的光照不均匀，表现为当图像中亮的区域光线过强或暗的区域光照不足时，图像中的重要细节会被掩盖，为后续基于图像的应用带来困难。因此，对低照度图像增强的研究具有重要意义。

目前，针对低照度图像增强已有很多研究成果。如:直方图均衡的算法、基于Retinex 理论的算法、基于暗通道先验的算法、伽马校正的算法等。传统的直方图均衡法对整体亮度一致的图像具有较好的增强效果，但对于照度不均的图像而言，直方图均衡法会出现过饱和问题。为解决这一问题，一些自适应或带有阈值限制、对比度限制的算法被陆续提出［1-5］，但这类算法往往很难确定准确的阈值。基于Retinex 理论的算法中最经典的是单尺度Retinex（Single Scale Retinex，SSR）算法和多尺度Retinex（MultiScale Retinex，MSR）算法，但基于该理论增强后的图像存在较严重的光晕现象，且色彩失真。文献［6］提出了一种基于双边滤波的Retinex 算法，在一定程度上减少了光晕现象，但未完全消除。随着新理论的发现，一些新的算法也被陆续提出，暗通道先验理论是He 等［7］提出的一种图像去雾理论，Dong 等［8］根据低照度图像的反转图和雾天图像具有一定的相似性，提出了基于暗通道先验的低照度图像增强算法，但由于低照度图像的反转图并不完全符合暗通道先验理论，因此该算法恢复后的图像整体偏暗且色彩失真。

综上，低照度图像增强算法中存在的主要问题是，增强后的结果存在过饱和或者色彩失真，这是因为未充分考虑低照度图像照度不均的问题。因此，可以通过估计原始图像的光照分量，对于光照较强的区域适当降低亮度，对于光照较弱的区域适当增强亮度，便可将被掩盖的细节重现，同时保证色彩不失真。文献［9］提出的自适应双向保带宽对数变换算法和文献［10］提出和光照不均的自适应增强算法，都是基于此思想，先通过一定的方法估计原始图像的光照分量，再根据光照分量进行自适应增强，从而消除光照不均对增强效果的影响。但文献［9］是通过对原始图像变换后得到变换后图像的亮度，并非是原始光照分量；文献［10］中估计光照分量的算法并不准确，提出的增强算法也不适用于低照度图像。因此，本文提出了一种新的低照度图像增强算法，主要工作如下:1）提出了最大差值图像的概念，并将交替引导滤波用于最大差值图像，实现光照分量的精确估计；2）设计了图像亮度自适应的伽马变换，能够根据图像的光照分量自适应调整经典伽马变换参数。实验结果表明，本文算法在增强暗区细节的同时，能够有效抑制过亮区域灰度值，对低照度图像增强具有较好的效果。

1 光照分量估计

在一幅低照度图像中，图像的整体灰度值较低，且往往存在多个光源，这给光照分量的估计带来一定困难。而准确估计出光照分量，是增强低照度图像视觉效果的关键因素。

Retinex 理论指出，一幅图像由光照分量和反射分量共同构成，可以表示为:

其中:J 为观测得到的图像:R 为图像的反射分量:L 为光照分量。物体本身的颜色由其反射分量决定，与光照分量关系不密切，即物体本身的色彩不受光照非均匀性的影响，故可以通过消除或降低光照分量L，得到的反射分量R即为增强后的结果；而反射分量对应原始观测图像的高频成分，光照分量对应低频成分，因此可以对原始图像进行低通滤波得到光照分量L，再通过式（1）即可得到R。

SSR 和MSR 正是基于这种思想，将原始图像和高斯低通滤波器进行卷积，从而获取光照分量。但高斯滤波器缺乏边缘保持能力，因此导致光照分量估计不准。文献［9］利用引导滤波保边平滑的功能来获得光照分量，但引导滤波得到的光照分量又包含过多的细节信息，不符合光照分量对应图像中低频成分这一特征。

本文针对低照度图像提出的估计光照分量新方法是:通过红绿蓝（Red Green Blue，RGB）空间三通道间的最大差值图获得初步光照分量，利用交替引导滤波进行校正，从而准确估计出图像的光照分量。

1.1 最大差值图

假设一幅低照度图像为J(x，y)，对式（1）两端进行对数运算，变换后可得:

对于低照度图像，尤其是较暗的区域，由于场景中的物体几 乎 没 有 反 射 特 性 ，可 认 为 ln R(x，y) ≈0，即ln J(x，y) ≈ln L(x，y)。由于较暗区域的光照分量几乎为0，即L(x，y) ≈0，为了避免这种情形，可取变换后R、G、B 三通道的最大差值，即

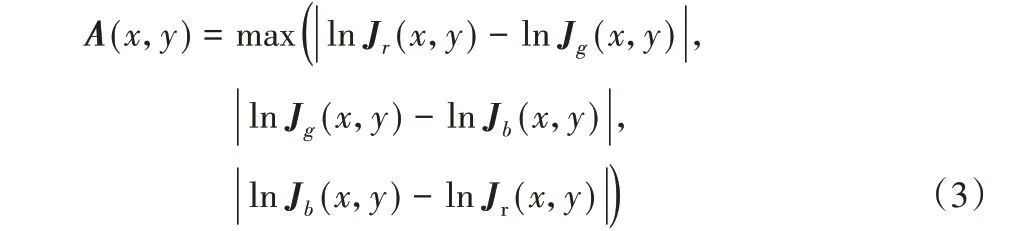
作为ln L(x，y)的估计，最终通过式（4）反变换得到光照分量的初步估计结果:

从图1 结果可以看出，求取三通道最大差值的方法能够得到初步的光照分量，且结果图像中细节信息得到平滑，同时保留了重要边缘，所得结果与原图像的光照分布具有高度的一致性。这是因为，对一幅低照度图像来说，图像中大部分像素亮度较低，这些像素点在R、G、B 三通道的灰度值都较低，导致三通道间灰度值相差较小，求取最大差值后各个像素的灰度差别也较小，因此具有平滑的效果。

图1 RGB图像的最大差值图Fig.1 Maximum difference image of RGB image

图2为图1实验结果的水平灰度扫描对比。

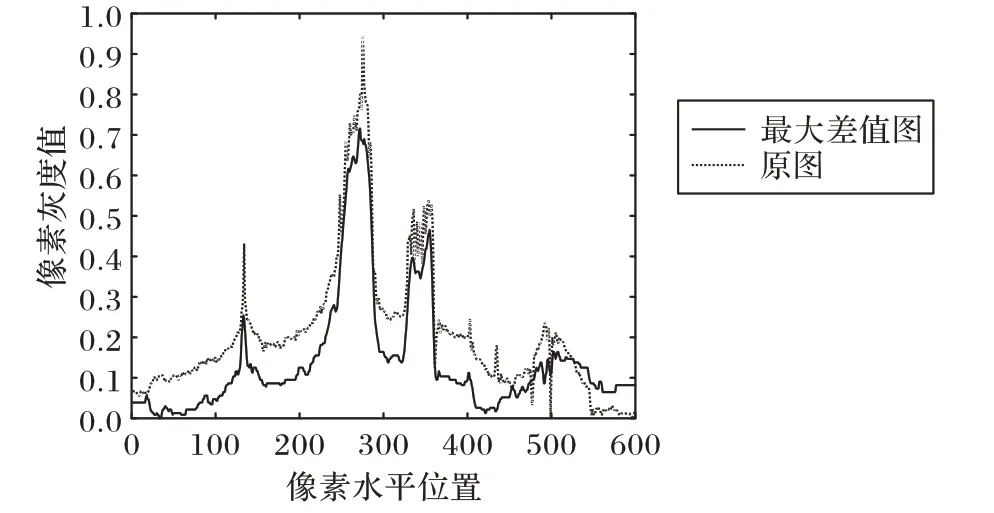
图2 原图和最大差值图水平灰度扫描对比（图1的第200行）Fig.2 Horizontal grayscale scanning comparison between original image and maximum difference image（line 200 for Fig.1）

从图2 可看出:最大差值图确实具有一定的平滑功能，但并不完全符合原始图像的光照分布，这是因为，在低照度图像中同样存在较亮区域，通过最大差值求取光照分量的原理并不适用高亮区域。因此，可将最大差值图作为初步的光照分量，但需要进一步的修正。

1.2 光照分量校正

通过上述实验分析可知，虽然低照度图像的最大差值图基本符合光照分量的特征，但依然存在两点不足:其一，最大差值图中仍然包含一定的图像细节，不完全符合光照分量对应图像中低频成分这一特征；其二，从图1 中方框对应区域可以看到，当原图像中存在强光源时，最大差值图中对应区域会出现中心暗斑现象，和原始图像的光照分布不相符，这是因为强光源中心接近白光，其R、G、B 三通道的灰度值接近相等，因此求取最大差值的结果接近于0。为了解决上述问题，本文采用了交替引导滤波的方法对最大差值图进行校正。

1.2.1 引导滤波

引导滤波由He 等［11］最早提出。引导滤波过程需要满足两个条件:一是输出图像O 和引导图像G 要满足局部线性关系，即

其中:ωk是半径为s的滤波窗口；中心像素点为k；（ak，bk）为滤波窗口内的局部线性系数；Gi为引导图中的像素i；Oi为输出图像中的像素i。局部线性关系保证了输出图像和引导图像具有梯度一致性（引导滤波的保边特性来源于此）。

引导滤波的第二个条件，要使得输出图像和输入图像之间尽可能相似，这里采用了最小二乘法的思想，使下述代价函数E(ak，bk)达到最小值:

其中:E(ak，bk)为窗口ωk的代价函数；G 为引导图像；I 为输入图像；ε为正则化参数。由式（6）可以求得:

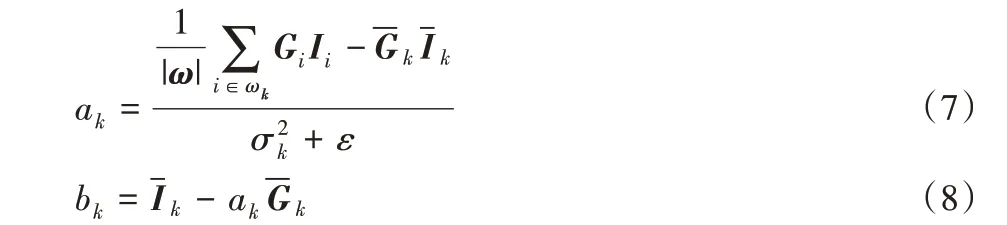
其中:|ω|为ωk内的像素个数和为输入图像I 和引导图像G在滤波窗口ωk内的均值；为I在ωk内的方差。得到ak、bk后便可利用式（5）得到滤波窗口内输出图像的各个像素值。但是，由于每一个像素i 会被多个滤波窗口包含，这导致同一个像素i 的输出值Oi在不同滤波窗口中得到不同结果，因此需要对同一像素得到的所有输出值进行加权平均，即

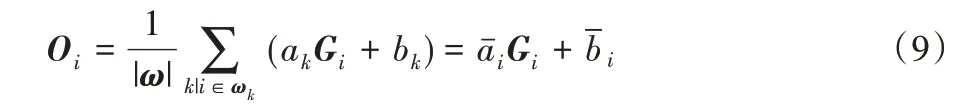
理论研究以及实验结果证实，引导滤波在平滑图像的同时也尽可能地保持了图像边缘信息。

1.2.2 交替引导滤波

通过1.2.1 节分析可知，引导滤波可以实现对输入图像中细节的平滑，尤其当输入图像和引导图像相同时，可以有效降低细节信息，同时保留边缘信息。这就解决了最大差值图中仍然包含一定数量的图像细节这一问题。本文将最大差值图同时作为引导图和输入图进行引导滤波，滤波窗口大小为4 × 4。从图3（b）实验结果中可以看到，图像确实得到了进一步平滑，更加符合光照分量的特征。

图3 光照分量校正过程Fig.3 Light component corrrection process

但是从图3（b）测试结果中依旧可以看到，图像中的强光源区域灰度值依旧过低（仍然存在中心暗斑），不符合原图像光照分布特征。由1.2.1 节分析可知，引导滤波是基于最小二乘法的思想，从而保证引导图像和输入图像间的差别最小化。由于采用最大差值图同时作为输入图和引导图，所以强光源部分无法得到修正。

通过选择合适的引导图和输入图再次进行引导滤波可以解决此问题。将原始图像作为输入图，从图3（b）所示的实验结果作为引导图，再次进行引导滤波，从图3（c）所示的实验结果表明，强光源区域确实得到了修正。但同时图像的细节部分也被恢复了一部分，这是因为输入图为原始图像，引导滤波会导致输出结果向原始图像靠近，因此在修正强光源部分的同时，一部分细节信息也被恢复，这是不希望看到的。

综合以上分析，第一次引导滤波使图像细节信息得到平滑，但强光源部分不符合原图像的光照分布特征；第二次引导滤波使得强光源部分得到了修正，但细节信息又被恢复了一部分。因此，本文采用交替引导滤波对初始光照分量进行校准，从而获取图像的准确光照分量。即采用多次迭代，每次迭代将前次迭代结果和原始图像交替作为引导图及输入图进行引导滤波:

其中:Gt-1为上次引导滤波的结果；J为输入图像；γ为滤波窗口大小；ε 为正则化参数；guidedfilter 为引导滤波函数。迭代的起始为最大差值图D(x，y)自身引导滤波的结果。

具体过程如图4所示。交替引导滤波的具体步骤如下:

将最大差值图D(x，y)同时作为引导图和输入图进行引导滤波，得到的结果D1(x，y)作为输入图，用原始图像J(x，y)作为引导图再次引导滤波。然后进行如下交替迭代:

步骤1 将前次迭代结果Gn-1作为输入图像，原始图像J(x，y)作为引导图进行引导滤波；

步骤2 将步骤1结果作为引导图，原始图像J(x，y)作为输入图像进行引导滤波；

步骤3 根据迭代次数，重复步骤1和步骤2，最终得到的结果Gn即为所求光照分量。

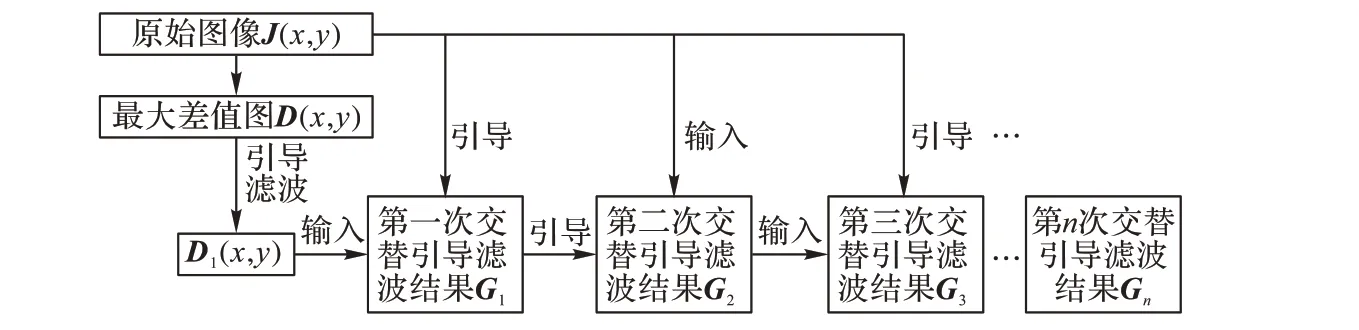
图4 交替引导滤波过程Fig.4 Alternating guided filtering process

图3（d）为交替引导滤波后的结果（迭代次数n=5，滤波窗口γ = 4 × 4，正则化参数ε=0.01），可以看到，交替引导滤波后的图像在保持边缘的同时，细节部分得到了平滑，同时强光源部分也得到了修正，完全符合原始图像的光照分布特征。

为了进一步验证本文算法得到的光照分量效果，分别与多尺度高斯滤波（尺度因子分别为15、80、250）和文献［10］中的引导滤波两种获得光照分量的方法进行比较。

通过图5～6 实验结果可以看出，三种方法都能够提取出光照分量，但相较而言，多尺度高斯滤波方法缺乏边缘保持能力，尤其是图像中强光源部分，平滑后体现不出强光源的特征；引导滤波方法得到的光照分量虽然准确，但包含的细节信息过多；而本文方法得到光照分量不仅保持了重要边缘，同时足够平滑，可以准确地表示原始图像的光照分布特征。

图7 为图5 中各个图像的灰度水平扫描曲线（第200 行），从中可看出:高斯滤波的结果中一些重要的边缘被过度平滑，而引导滤波的结果细节信息过于丰富，只有本文方法在平滑图像的同时保留了重要边缘。

图5 光照分量效果比较1Fig.5 Comparison of light component effect 1

图6 光照分量效果比较2Fig.6 Comparison of light component effect 2

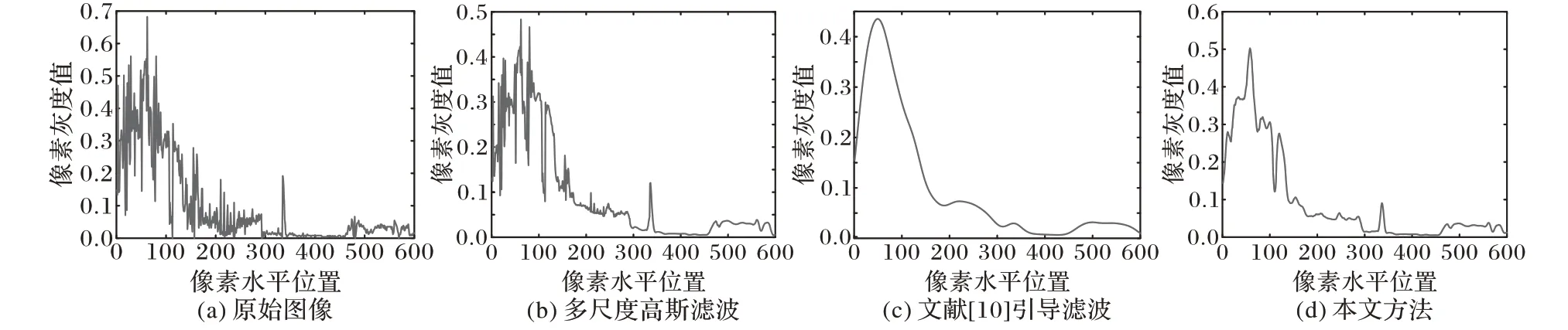
图7 图5的光照分量灰度水平扫描曲线对比Fig.7 Horizontal graylevel scanning curve comparison of illumination components of Fig.5

2 改进的伽马变换

通过交替引导滤波得到光照分量后，需要根据光照分量对原始图像进行增强，消除光照不均带来的影响。本文采用基于伽马变换的自适应增强算法。

伽马变换具有改善图像质量、校正光照分布的功能，且计算简单，因而应用广泛。伽马变换的一般表达式如下:

y =(x + esp)γ（11）其中；x 与y 的取值范围为［0，1］；esp 为补偿系数；γ 为伽马系数［12］。

通过调整γ 可以改变输入图像x 和输出图像y 之间的映射关系，如图8 所示。可以看到:当γ＜1 时，输入图像中灰度值较低的部分得到增强；当γ＞1时，灰度值较高的部分受到抑制。多数伽马变换都是手动设置伽马系数，为全局变量，对于低照度图像的增强效果并不理想［13］。

文献［10，14］中提出了一种自适应伽马变换，能够根据光照分量自适应调整伽马系数γ，从而消除光照不均的影响。但该方法并不适用于低照度图像，本文在此基础上对伽马变换进行了改进，设计了一种适用于低照度图像的自适应伽马变换的算法，能够在增强图像的同时有效消除低照度图像中光照不均带来的影响。具体表达式如下:

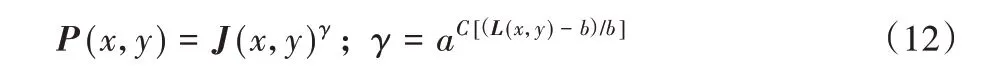
其中:P(x，y)为增强后的图像；J(x，y)为原始输入图像；L(x，y)为第1 章得到的光照分量，b 为理想的光照强度，取值范围为［0，255］。原始图像的光照分量低于b 的像素应该得到增强，高于b 的像素应该受到抑制，文献［14］中b 的取值为光照分量的均值。由于低照度图像平均灰度值较低，若将光照分量的均值作为b 值，会导致大部分像素受到抑制，增强后的图像整体灰度值会过低，因此经实验对比后，本文中b的取值为光照分量最大灰度值的1/2。

由图8 伽马变换的性质可知，应当在原始图像光照分量较低（L(x，y) - b ＜0）时，伽马系数要小于1，使这部分图像得到增强；当原始图像光照分量较高(L(x，y) - b ＞0)时，伽马系数要大于1，使这部分图像受到抑制。因此a 为一个大于1的值，经过大量实验后，本文中a 取值为2.2。由于低照度图像整体对比度较低，为了增强视觉对比度，本文设置了调整系数C，取值为1.2。

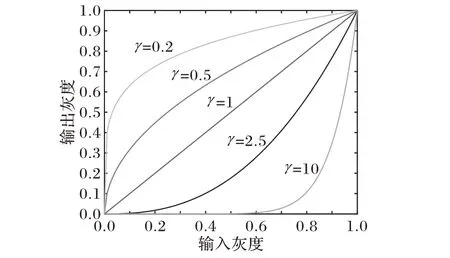
图8 0～1范围内的伽马变换示意图Fig.8 Schematic diagram of Gamma transform in the range of 0-1

图9 为理想光强b 取值为128（归一化后为0.5）时本文的自适应伽马变换曲线，从中可看出:当输入图像灰度值低于期望光强b 时，曲线为上凸，输入图像经变换后得到增强；在高于期望光强b时曲线为下凹，输入图像经变换后受到抑制。

图9 本文自适应伽马变换曲线（b的归一化值为0.5）Fig.9 The proposed adaptive Gamma transform curve（normalized value of b=0.5）

图10 是对图1（a）RGB 图像直接应用式（12）进行自适应伽马变换前后的直方图对比，从中可看出:由于本文算法根据亮度自适应调整伽马系数，因此能有效消除光照不均的影响，使原图像中过亮的区域得到了抑制，过暗的区域得到了增强，压缩了图像的动态范围。

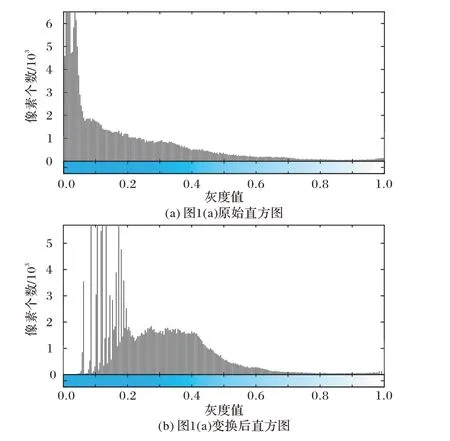
图10 本文自适应伽马变换前后直方图对比Fig.10 Histogram comparison before and after adaptive Gamma transform proposed in this paper

3 本文算法步骤

本文提出的低照度图像增强具体算法步骤如下:

1）将原始图像J(x，y)变换到RGB 域，通过1.1 节中的方法求取最大差值图D(x，y)；

2）将D(x，y)同时作为输入图和引导图进行引导滤波，得到初步光照分量D1(x，y)；

3）将得到的D1(x，y)和原始图像J(x，y)分别作为输入图像和引导图像进行交替引导滤波，得到校正后的光照分量L(x，y)；

4）根据得到的光照分量L(x，y)，通过式（12）进行自适应伽马变换，对原始图像J(x，y)进行增强，得到最终的结果P(x，y)。

4 实验与结果分析

为了验证本文算法的可行性和有效性，本章对多幅像素为600 × 400的低照度图像，分别从增强的主观视觉效果及客观指标参数两个方面进行分析比较。实验环境:CPU 为Inter Core i5-7500@3.4 GHz、内存为4 GB、Windows10 操作系统的PC，Matlab2016a软件实现相关算法。

4.1 主观评价

针对夜间低照度图像，分别与伽马变换、带色彩恢复的多尺度视网膜增强（Multi-Scale Retinex with Color Restoration，MSRCR）算法、文献［9］算法和文献［10］算法进行比较，实验结果如图11～13所示。

通过实验对比可以发现，伽马变换的算法虽然整体效果较好，但是对于图像中亮度较高的区域，增强后灰度值变得更大，掩盖了部分细节信息，如图11（b）中的车灯以及图13（b）中的路灯，增强后车灯和路灯的光线使附近的细节信息都被掩盖；MSRCR 算法得到结果整体对比度较高，但从图11（c）和图13（c）实验结果可以看到，存在较为严重的色彩失真、噪声放大问题，对于亮度较高的区域同样没有抑制效果；文献［9］算法增强后图像的色彩保持较好，但在图11（d）中可以看到，对过亮区域的抑制效果不明显，同时在图12（d）和图13（d）中，对过暗区域的增强也不够；文献［10］算法增强后的结果确实在一定程度上消除了光照不均带来的影响，但是增强后的结果整体灰度值较低，亮区域被过度削弱，这是因为文献［10］算法光照分量估计不准，同时自适应伽马变换算法并未针对低照度图像进行优化。本文算法相较其他算法，不仅增强效果好，增强后色彩无失真，最大的优点在于，对于亮度较高的区域具有较好的抑制效果，能够在增强图像整体亮度同时，还原出高亮度区域的细节信息，图11（f）中的车灯和图13（f）中的路灯效果尤为明显。

图11 实验结果1Fig.11 Experimental result 1

图12 实验结果2Fig.12 Experimental result 2

4.2 客观评价

图像的平均梯度是图像清晰度的重要体现，能反映图像的细节信息；信息熵可以体现图像所携带信息量的多少，表征图像的复杂程度；标准差可以反映图像的对比度特征。为了进一步客观比较不同算法的增强效果，本文选取以上几个指标作为图像的客观质量评价标准。图11～13 对应的评价数据如表1所示。从表1的指标对比结果可以看出:本文算法在信息熵和平均梯度的对比中结果较好，说明本文算法可以有效恢复图像细节信息，还原图像原始信息；但是在标准差的对比中无明显优势，这是因为本文算法对亮度值低于期望光强的区域有增强效果，而对亮度值高于期望光强的区域有抑制效果，从而导致和其他算法相比，增强后的整体对比度偏低。但从主观实验结果已经看到，实际增强效果要优于其他算法。

表1 各类算法评价指标对比Tab. 1 Comparisons of evaluation indicators of different algorithms

5 结语

针对低照度图像整体亮度低、光照不均匀等问题，本文提出一种新的图像增强算法。本文的主要工作包括:提出了通过最大差值图像结合交替引导滤波的方法估计光照分量；同时提出了针对低照度图像的自适应伽马变换。实验结果表明，本文算法估计的光照分量十分准确，最终增强后的图像在保证整体效果的同时，能够有效抑制过亮区域，使结果呈现出更多的图像细节，增强后的图像平均梯度提升1 倍以上，信息熵提升14%以上，说明了本文算法的有效性和优越性。但目前的研究缺少对光照分量准确度定量的衡量方法，后续将重点针对这方面进行研究。同时本文算法增强后的图像整体灰度值偏低，导致结果较暗，在后续研究中，重点考虑在保证目前增强效果的同时，进一步增强图像亮度。