基于随机支撑挑选的广义正交匹配追踪算法

徐志强，蒋铁钢，杨立波

（广东科技学院机电工程系，广东东莞523083）

（∗通信作者电子邮箱jiangtiegang5201@163.com）

0 引言

作为一种新的亚采样技术，压缩感知（Compressed Sensing，CS）理论［1］以其以远低于香农-奈奎斯特采样定理所要求的采样数重构原始信号的特点，在过去的几年引起了研究人员的广泛关注。CS 理论自提出以来，在信号处理、图像处理、人工智能、无线通信等领域得到了广泛的应用［2］。CS理论的主要思想是在已知信号的稀疏先验信息情况下，将稀疏信号投影到低维空间，再通过求解一个稀疏约束的优化问题来重建原信号。根据这一思想，压缩感知的研究范围主要包括信号的稀疏表示、测量矩阵的设计和重构算法的设计。

重构算法作为影响信号重建性能的关键因素，吸引了众多学者的研究，近年来已提出了一大批有效的重构算法。这些算法主要包括基于ℓ1范数的凸优化算法和基于ℓ0范数的贪婪追踪算法。凸优化类算法将稀疏约束的欠定问题转化为凸问题来求解，如基追踪（Basis Pursuit，BP）方法［3］、内点法［4］、梯 度 投 影 法（Gradient Projection for Sparse Reconstruction，GPSR）［5］等。凸优化类算法具有良好的理论保证和重构性能，但是其复杂度很高，在求解大规模问题时并不实际。基于ℓ0范数的贪婪追踪算法则是通过迭代地寻找待恢复信号的正确支撑，并以此支撑来构造原信号的逼近信号，直到满足一定的误差条件。这类算法复杂度较低，算法操作简单，但是其重构精度表现不如凸优化类算法。经典的贪婪算法包括正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法［6］、正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP）算 法［7］、子 空 间 追 踪（Subspace Pursuit，SP）算法［8］、压缩采样匹配追踪（Compressive Sampling Matching Pursuit，CoSaMP）算 法［9］和 广 义 正 交 匹 配 追 踪（Generalized Orthogonal Matching Pursuit，GOMP）算法［10］等。这些算法通过在每次迭代中挑选一个或多个原子来逐步逼近原始信号，具有较强的理论保证。然而大多数实际应用中信号的稀疏度不可知，这限制了上述算法的应用，为了解决这一问题，文献［11］提出了稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法，该算法将信号的重构过程划分为具有固定步长的几个阶段，并且无需稀疏度先验信息。文献［12］在共轭梯度迭代硬阈值算法［13］的基础上，结合SP 算法的回溯思想，提出了基于回溯的共轭梯度硬阈值迭代（Backtracking-based Conjugate Gradient Iterative Hard Thresholding，BCGIHT）算法，该算法结合了硬阈值类算法支撑集挑选的优势和贪婪追踪类算法系数更新精确的优势，在一定程度上减少了算法的迭代次数。

作为贪婪算法中具有代表性的一种算法，GOMP 算法在迭代过程中引入回溯操作，允许支撑集中的元素个数大于稀疏度，这一方面加大了稀疏系数更新的计算量，另一方面影响了残差的更新。针对这一问题，文献［14］提出一种支撑回溯的GOMP 算法（BGOMP），该算法确保了每次迭代中支撑集的大小不超过稀疏度，在一定程度上降低了算法的复杂度。针对GOMP 算法重构精度不高的问题，文献［15］提出了一种多候选集GOMP 算法，该算法在迭代初始设置了多个候选支撑集，并迭代地将新匹配的原子加入到候选集中，最后挑选出残差能量最小的候选集作为支撑集，使算法的重构精度有了较大提高，但是同时也加大了其算法复杂度。

最近，受随机梯度（Stochastic Gradient）方法的影响，针对稀疏约束优化问题，文献［16］提出了随机硬阈值迭代（Stochastic Iterative Hard Thresholding，StoIHT）算法和随机梯度匹配追踪（Stochastic Gradient Matching Pursuit，StoGraMP）算法，StoIHT 算法与IHT 算法的不同之处在于前者在每次迭代中只随机地计算了部分梯度，而后者则需计算全部梯度。与之类似的有最近提出的随机压缩采样匹配追踪算法［17］（Stochastic Compressive Sampling Matching Pursuit，StoCoSaMP）和 随 机 梯 度 追 踪（Stochastic Gradient Pursuit，SGP）算法［18］。这类算法在求解大规模问题时能大幅减少计算量，但是由于梯度信息的不全面，该类算法通常需要比具有完整梯度信息的算法需要更多的迭代次数。

本文针对GOMP 算法在每次迭代中需要对测量矩阵和残差进行匹配计算，导致其算法复杂度高、重构时间长的问题，引入随机支撑挑选的思想，提出了一种基于随机支撑挑选的广义正交匹配追踪（Stochastic Support Selection based Generalized Orthogonal Matching Pursuit，StoGOMP）算法。该算法在迭代过程中根据给定的概率来判断是否需要进行匹配计算，如果判断为需要进行匹配计算，则按照GOMP算法的流程继续执行；如果判断为不需要进行匹配计算，则生成一个随机支撑集作为候选集。这种方式在一定程度上考虑了单次迭代的计算复杂度与迭代总次数的相互影响，在选择合适的初始概率时，能有效降低算法的计算量。

1 压缩感知理论

对于长度为N × 1 的信号h ∈RN×1，它可以表示成一组正交基的线性组合，即:

如果其表示系数x 中仅有K(K ≪N)个元素的绝对值大于零，则称信号h 在基ψ ={ψi}Ni=1上是K-稀疏的。这里ψi表示基矩阵ψ ∈RN×N的列原子。在压缩感知理论中，稀疏信号通过一个大小为M × N(M ≪N)的采样矩阵Φ 进行采样，得到测量值向量y ∈RM×1，这一过程可以描述为:

其中:A = Φψ称为测量矩阵。由式（2）可知，测量值向量的维度远低于信号的维度，因此式（2）是一个欠定问题，有无穷多个解，这意味着很难从测量值向量y中重构出稀疏系数x。由文献［2］可知，当测量矩阵满足有限等距限制（Restricted Isometry Property，RIP）时，重构x的过程就等价于求解如下ℓ0范数最小化问题:

其中:||⋅||0表示x 中非零元素的个数。有限等距性质可以描述成:

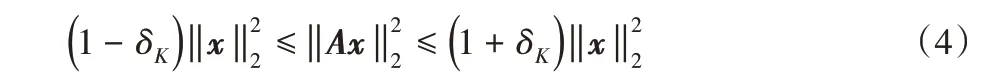
其中:δK表示对于所有x 满足式（4）的最小常数。当有限等距常数δK≤ 2 - 1 时，式（3）可以转化为如下ℓ1范数最小化问题:

其中:||⋅||1为向量的ℓ1范数，表示向量元素的绝对值之和。文献［2］表明，对于给定的稀疏基，当采样矩阵为服从高斯分布的随机矩阵时，测量矩阵在很大概率上满足RIP条件。

2 基于随机支撑挑选的GOMP算法

2.1 算法描述

StoGOMP 算法（具体见算法1）的输入参数包括测量矩阵、测量向量、稀疏度、每次迭代挑选的索引数、给定的误差阈值和给定的概率值。在迭代过程中，StoGOMP 算法的迭代主体为步骤2～7:步骤2 在区间［0，1］内随机挑选一个值p，将该值与输入的概率Pr进行比较；步骤3中，若p小于Pr，则在测量矩阵的列原子中随机挑选S 个原子的位置用于合并支撑集；步骤4 中，若p 大于Pr，则在测量矩阵与残差的内积中挑选绝对值最大的S个元素的位置用于合并支撑集；步骤5中将当前迭代中选择的支撑位置合并到前一次迭代的支撑集中，将合并的支撑集作为候选支撑集，这类似于子空间追踪算法中的支撑集回溯操作；步骤6 使用最小二乘法来更新稀疏系数，可以起到去偏作用，使更新结果更加精确；步骤7 更新残差。步骤2～4是StoGOMP 算法与原GOMP 算法不同的地方。由文献［10］可知，GOMP 算法的计算量主要集中在测量矩阵与残差的内积计算上。StoGOMP 算法采用随机的方式挑选支撑集，一定程度上减少了匹配计算的次数，然而随机挑选支撑由于存在很大的不确定性，使迭代过程中某些支撑被反复选择，导致迭代次数增加。为了控制支撑集挑选的精确性和迭代计算量，StoGOMP 算法将是否需要计算测量矩阵与残差的内积划分到了2 个概率区间，可以根据预先设定的概率值来进行决策，从而起到平衡计算量与迭代次数的作用。

2.2 StoGOMP算法性能分析

以下分三种情况对StoGOMP算法进行分析:

第一种情况:Pr= 1。此时StoGOMP 算法退化为GOMP算法，根据文献［10］可知，对于高斯随机采样矩阵，StoGOMP算法的采样数仅需要M = O(K log (N/K))个，并且具有与GOMP算法相同的理论保证。

第二种情况:Pr= 0。此时，StoGOMP 算法无需计算测量矩阵与残差的内积，完全随机地从测量矩阵的列原子中挑选支撑集，这大大减少了算法的计算量。然而，每次迭代中随机挑选支撑集可能会导致某些原子在当前迭代中被选择，而在下一次迭代中又被丢弃，导致支撑被反复选择，增加算法的迭代次数。由文献［18］可知，在有限迭代次数内，即使Pr= 0，算法最终能找到正确的支撑集。

第三种情况:0 ＜Pr＜1。此时StoGOMP 算法需要计算测量矩阵跟残差的内积的概率为1- Pr，这意味着Pr的大小影响着算法的计算复杂度。同时，随机挑选的支撑并不精确，导致迭代次数过多。因此，计算复杂度和迭代次数需要通过控制Pr的大小来调节。

算法复杂度分析:GOMP 算法中，测量矩阵与残差的内积计算量约为2MN 次乘法运算，稀疏系数估计的计算量约为4S2M 次乘法运算，残差更新计算量大约为2SM 次乘法运算。设GOMP算法迭代次数为k，则重构过程总的计算量可以估计为k(MN +(4S + 2)SM)次乘法运算。StoGOMP 算法中，设迭代次数为j，计算测量矩阵与残差的概率为1- Pr，则其总的算法复杂度可以估计为j(1- Pr)(MN +(4S2+ 2S)M)次乘法运算。从GOMP算法和StoGOMP算法的复杂度对比可以看出概率值Pr的选择是决定StoGOMP算法复杂度的关键因素。

3 实验与结果分析

本章使用随机高斯信号和数字图像作为测试信号，对比了OMP 算法、SP 算法、CoSaMP 算法、GOMP 算法、BGOMP 算法和StoGOMP 算法的重构性能。所有实验均在Intel（i5-7500，8 GB 内存）平台上完成，所使用的仿真软件为Matlab2018B。

3.1 随机高斯信号重构实验

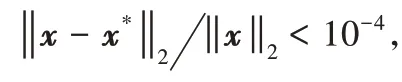
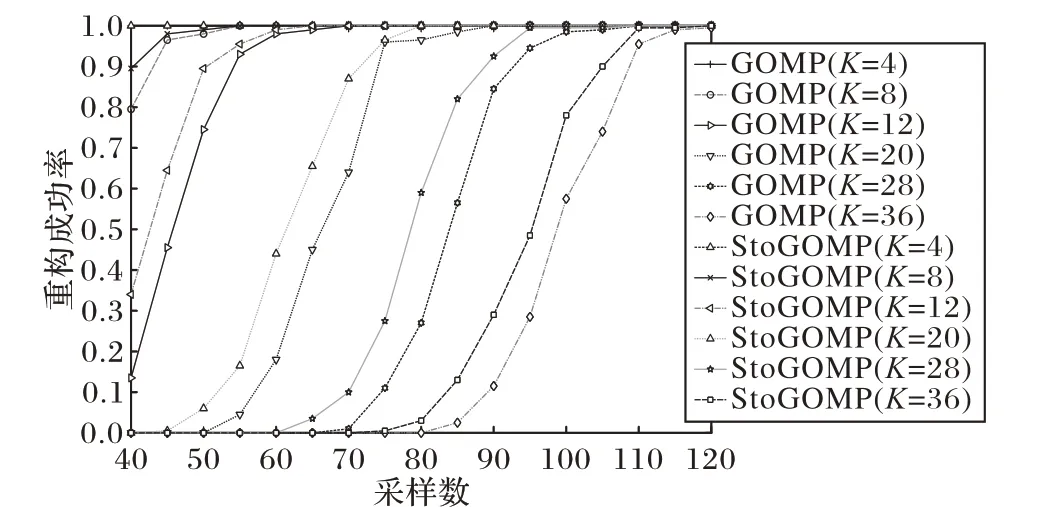
图1 不同稀疏度情况下，GOMP算法和StoGOMP算法在不同采样数情况下的重构成功率比较(S = K 2，Pr = 0.5)Fig. 1 Comparison of reconstruction success rates of GOMP algorithm and StogoMP algorithm under different sparsity conditions(S = K 2，Pr = 0.5)

为了验证StoGOMP算法的重构精度，以长度为400 × 1的高斯信号为测试信号，大小为100 × 400的随机高斯矩阵作为采样矩阵，稀疏度设置为K = 24，每次迭代挑选的索引数设置为［5，10，15］，Pr= 0.3。图2 记录了平均重构误差与迭代次数的关系。由图2可知:在迭代次数小于20次时，GOMP 算法与BGOMP 算法收敛速度相当，且都比StoGOMP 算法快；当迭代次数大于20时，GOMP算法的重构误差下降缓慢，误差曲线基本保持水平，而StoGOMP 算法的误差曲线还有明显下降。这说明在迭代后期，StoGOMP 算法在重构精度上具有优势。这是因为在迭代后期GOMP 算法挑选的原子基本不再变化，因此其重构误差变化非常缓慢，而在StoGOMP 算法中，在某些步骤可能有新原子的加入，这些新原子的索引构成的支撑集可能是比GOMP 算法得到的支撑集更优的支撑集，其重构误差因此更小。

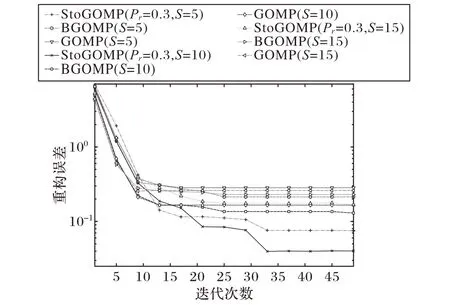
图2 不同算法平均重构误差与迭代次数的关系Fig. 2 Relationship between average reconstruction error and number of iterations of different algorithms

为了验证给定概率Pr对StoGOMP 算法重构性能的影响，采用长度为N = 200，500，1 000，2 000 的高斯信号作为测试信号，稀疏度设置为K = 40，100，200，400，采样数设置为M =N 2。从图3 所示的实验结果可看出，当Pr接近0 或1 时，StoGOMP算法的重构成功率最低，当0.2 ＜Pr＜0.8时，重构成功率保持在较高的水平，这说明Pr在区间［0.2，0.8］内取值比较好。

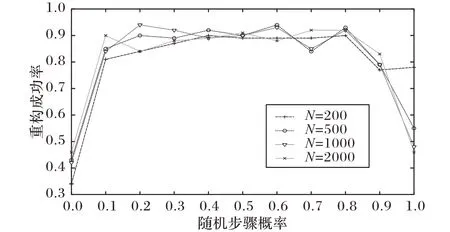
图3 重构成功率与设定概率Pr的关系Fig. 3 Relationship between reconstruction success rate and set probability Pr

为了验证StoGOMP 算法的重构性能，与其他常见贪婪追踪类算法进行重构对比实验。待测试高斯信号长度为256 ×1，采样矩阵大小为128× 256的随机高斯矩阵，稀疏度设置为8～80，间隔为4。从图4所示的实验结果中可看出，在Pr= 0.5时，在重构成功率方面，StoGOMP 算法的表现要优于其他算法。这是因为StoGOMP 算法在迭代过程中不仅将残差与测量矩阵内积的前K 个最大值作为候选支撑，而且还通过随机方式从所有位置挑选候选支撑，这在一定程度上增加了正确支撑集挑选的概率。

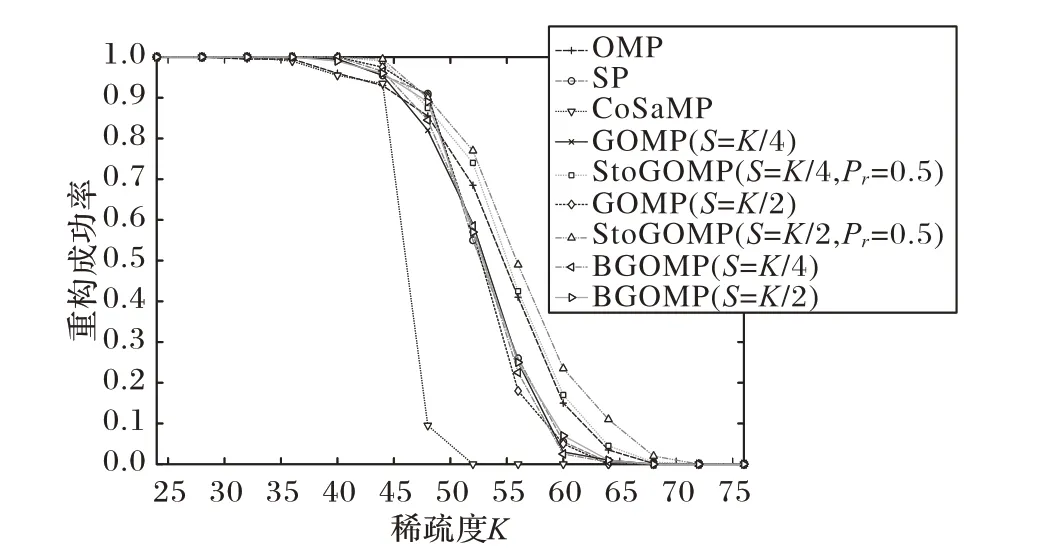
图4 不同算法重构成功率与稀疏度关系Fig. 4 Relationship between reconstruction success rate and sparsity of different algorithms

3.2 二维图像重构实验

实验采用大小为512 × 512 像素的某型号汽车法兰盘图像作为测试图像来验证本文算法的重构性能。实验中采用小波基作为稀疏基，稀疏度设置为K = M 4，定义采样率r =M/N。所有的重构算法均独立重复200 次取均值作为实验结果。实验采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）作为图像重构质量的评判标准，PSNR的计算公式为:

采样率为r = 0.3 时不同算法重构得到的直观效果如图5所示。从图5 可知，BGOMP 算法重构效果与GOMP 算法相差不大，在Pr取0.2 时StoGOMP 算法的重构效果与GOMP 算法相当，当Pr取0.4时重构效果稍差。

图5 不同算法重构结果对比Fig.5 Comparison of reconstruction results of diffident algorithms

表1 为在不同采样率下不同算法重构汽车法兰盘图像的PSNR 值和耗时统计。表1 中:GOMP 算法参数为S = K 2，StoGOMP算法的概率值设为Pr= 0.2和Pr= 0.4。

从表1可知，当Pr= 0.2时，StoGOMP算法的重构PSNR值均高于同采样率下其他算法的PSNR 值，随着Pr的增大，StoGOMP 算法的重构PSNR 值呈现下降趋势。在不同采样率情况下，StoGOMP 算法重构时间均小于GOMP 算法和BGOMP算法，在采样率为r = 0.5 时，StoGOMP 算法的重构时间相比GOMP 算法减少了27%以上。在采样率较低时，GOMP 算法和StoGOMP 算法所需的重构时间高于OMP 算法和SP 算法，在采样率r = 0.3 和r = 0.5 时，前者所需重构时间明显低于后者。

为了验证StoGOMP 算法的抗噪性，对原始的汽车法兰盘图像加上不同程度的高斯白噪声，在采样率为0.3 时用各算法对加噪后的图像进行重构，重构结果记录在表2中。从表2可知随着噪声强度增加，各算法的PSNR值也逐渐降低。

表1 某型号汽车法兰盘图像用不同算法重构得到的PSNR和重构时间Tab. 1 PSNR and reconstruction time of flange image of a type of vehicle reconstructed by different algorithms

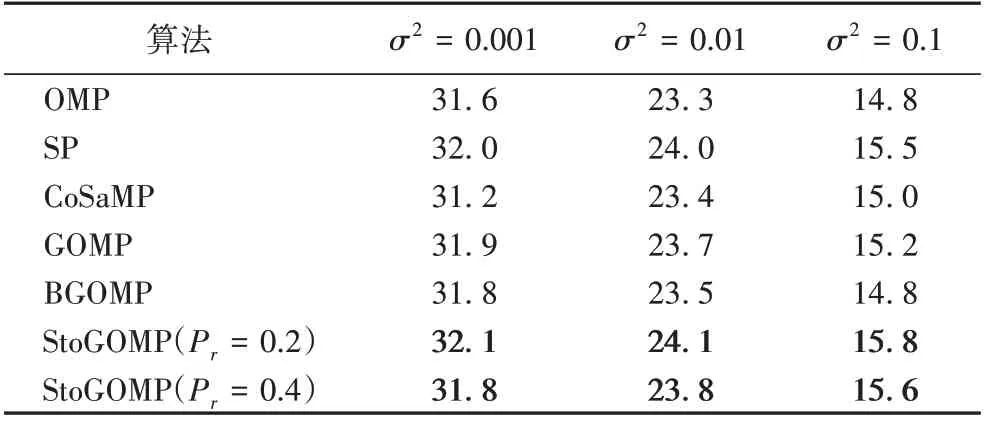
表2 高斯噪声环境下不同算法重建PSNR（r = 0.3）单位：dBTab. 2 Reconstruction PSNR of different algorithms in Gaussian noise environment（r = 0.3） unit:dB

对比表1 和表2 可以看出，StoGOMP 算法的重构PSNR 值变化幅度相对GOMP 算法较小，这说明其抗噪性能较好。这是因为StoGOMP 算法在迭代过程中某些支撑集是通过随机方式挑选，使其具有良好的抗干扰性能。

4 结语

为了减少GOMP 算法的计算量和重构时间，在GOMP 算法的基础上，引入随机支撑集挑选的策略，提出了StoGOMP算法，并对算法性能作了分析。StoGOMP 算法在某些步骤只需从测量矩阵中随机挑选支撑，无需计算测量矩阵和残差的内积，在一定程度上降低了算法的复杂度。一维随机高斯信号和现实图像重构实验结果表明，StoGOMP 算法相比GOMP算法在保证重构成功率的情况下，所需的采样数有大幅减少；相对于同类贪婪追踪类算法，StoGOMP 算法具有更高的重构成功率和良好的抗噪性能。