带时间窗的同时取送货车辆路径问题建模及模因求解算法

张庆华，吴光谱

（北京科技大学机械工程学院，北京100083）

（∗通信作者电子邮箱zqhustb@163.com）

0 引言

近年来，我国经济迅速发展，人们对现代物流的服务要求也逐渐增多，从以往的仅仅只有收寄快递的需求，逐步发展到包含定点配送、上门揽件、同城配送、准时服务等多元化的物流需求。随着逆向物流导致客户退换货的增多，上门取件逐渐成为了物流服务中必不可少的一环。带时间窗的同时取送货车辆路径问题（Vehicle Routing Problem with Simultaneous Pickup-Delivery and Time Windows，VRPSPDTW）也随之备受关注。

VRPSPDTW 是在经典车辆路径问题（Vehicle Routing Problem，VRP）的基础上，增加了时间窗约束，车辆必须在客户指定的时间窗内对客户进行服务；同时还在为客户进行配送的基础上，增加了取货服务，车辆不仅要对客户进行配送服务，还要对在客户所在的位置进行取货，将客户所要寄送的货物运回配送中心。

同时取送货问题（Vehicle Routing Problem with Simultaneous Pickup-Delivery，VRPSPD）由Min［1］于1989 年首次提出；而VRPSPDTW 则由Angelelli 等［2］在2002 提出，并使用精确算法进行求解；Wang 等［3］使用遗传算法（Genetic Algorithm，GA）对VRPSPDTW 进行了求解，并在Solomon 测试算例［4］的基础上设计了测试算例；Liu 等［5］采用了遗传算法和模拟退火算法求解家庭医疗物流的VRPSPDTW；Wang 等［6］提出一种并行的模拟退火算法，对大规模的VRPSPDTW 进行了求解；王超等［7］采用离散布谷鸟搜索（Discrete Cuckoo Search，DCS）算法对VRPSPDTW 求解，并取得了较好的效果。

模因算法（Memetic Algorithm，MA）最早是由Moscato［8］提出的一种模拟文化进化的算法。遗传算法中的变异操作是随机的，在成千上万的变异操作中找到对适应度有所提升的解非常困难。而模因算法又称文化基因算法，模拟的是文化进化的过程，对于文化基因而言，基因总是向着前进的方向发展，基因的传播过程是在上一代基因中严格复制的，子代在继承父代优秀基因的同时，对子代变异操作不是随机的，而是在大量知识的基础上，向更好的方向发展的。

国内对模因算法的研究较少，而国外采用模因算法解决的一般是带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW），如Nagata 等［9］提出了一种基于惩罚函数的边界组合模因算法，以求解VRPTW；Nalepa 等［10］采用自适应参数的模因算法对VRPTW 进行了求解。目前国内外采用模因算法解决VRPSPDTW 的文献较少，本文采用基于引导弹射搜索（Guided Ejection Search，GES）［11］和边界组合交叉的模因算法对VRPSPDTW 求解，通过GES 进行初始种群生成，采用多种邻域结构提升算法的搜索效率，同时与多种算法进行比较，验证了本文提出的模因算法的有效性。

1 带时间窗的同时取送货车辆路径问题

1.1 问题描述

VRPSPDTW 是在传统车辆路径问题上引入时间窗，将客户需要服务的时间标示出来，在客户能够接受的时间内进行配送或取货，从而提高物流服务水平和服务质量。因此，本文针对带时间窗的同时取送货车辆路径问题进行模型构建和求解。

VRPSPDTW 研究一队车辆从配送中心出发对一系列客户进行配送和取货服务，要求对路径进行合理规划，在满足时间窗约束和车辆载重约束的前提下，使配送成本最小。本文研究的VRPSPDTW 描述如下:

1）研究若干车辆由配送中心向客户配送物品，车辆对客户除了配送货物，还可能要从客户位置取走货，物配送中心和客户的地理位置以及客户的货物量已知。

2）车辆从配送中心出发并最终返回配送中心，在配送的过程中每个客户只被访问一次，并满足该客户的配送需求或取货需求，车辆所装载的货物在任何时刻都不能超过车辆自身载重。关键时间节点在车辆从配送中心出发时和在客户位置取货后。

3）每个客户有自身所要求的时间窗，包括最早开始服务时间、最晚开始服务时间、服务时间。

4）车辆对客户进行配送的过程中，到达客户所在位置的时间不能晚于最晚开始服务时间，但可以早于最早开始服务时间。若早于最早开始服务时间，则车辆需要在客户位置进行等待，直到最早开始服务时间，才能进行配送或取货服务。

5）若一位客户同时具有配送需求和取货需求，则对该客户进行服务时，先进行卸货，再进行装货。

因此，本文研究的VRPSPDTW 是某配送中心向一定数量的客户提供配送服务，配送中心具有若干车辆，车辆具有相同的最大承载能力，配送中心与各个客户之间的距离和行驶时间已知，每个客户具有固定的配送需求和取货需求；同时客户要求有固定的时间窗，包括最早开始服务时间、最晚开始服务时间、服务时间。每辆车为若干个客户提供服务，只能在客户所要求的时间窗内对客户进行服务，若车辆在客户所要求的最早服务时间之前到达，则需要进行等待至最早服务时间，才能进行服务。要求在满足时间窗约束和车辆载重约束的前提下，对每个客户完成所需要服务。

本文所研究的问题主要目标是使车队的规模最小，即所使用的车辆数最少；次要目标是车辆配送的总距离最短。

1.2 模型构建

根据以上对VRPSPDTW 的描述，构建合理的数学模型，模型参数定义如下:

K:配送中心进行服务的车辆集合。

M:所有需要提供服务的客户总量。

Q:车辆的最大载重限制。

V:配送中心和所有需要提供服务的客户集合。

Vi，i ∈{1，2，…，M}:所有需要提供服务的客户。

V0:配送中心。

di，i ∈{1，2，…，M}:客户i对应的配送量。

pi，i ∈{1，2，…，M}:客户i对应的取货量。

si，i ∈{1，2，…，M}:客户i对应的服务时间。

s0:车辆在配送中心的服务时间，一般s0= 0。

ei，i ∈{1，2，…，M}:客 户i 可 以 接 受 开 始 服 务 的 最 早时间。

e0:车辆从配送中心离开的最早时间。

li，i ∈{1，2，…，M}:客 户i 可 以 接 受 开 始 服 务 的 最 晚时间；

l0:车辆返回配送中心的最晚时间。

cij（i ≠j），i ∈{0，1，…，M}，j ∈{0，1，…，M}:客户或配送中心i与客户或配送中心j之间的车辆行驶距离。

tij（i ≠j），i ∈{0，1，…，M}，j ∈{0，1，…，M}:客 户 或 配 送中心i与客户或配送中心j之间的车辆行驶时间。

ai，i ∈{1，2，…，M}:车辆到达客户i处时刻。

a0:车辆到达配送中心的时刻，一般a0= e0。

wi，i ∈{1，2，…，M}:车辆在客户i处等待的时间。

oij，i ∈{1，2，…，M}，k ∈K:车辆k在离开客户i时，车辆的装载量。

o0k:车辆k在离开配送中心时的装载量。

X(i，j，k)（i ≠j），i ∈{1，2，…，M}，j ∈{1，2，…，M}，k ∈K:表示在车辆k 在执行配送或取货任务时，是否由客户i驶向客户j。X(i，j，k)= 1 表示车辆k 对客户i 进行服务后，随即对客户j 进行服务。X(i，j，k)= 0表示车辆k对客户i进行服务后，下一个服务对象不是客户j。

根据上述参数，建立数学模型如下:

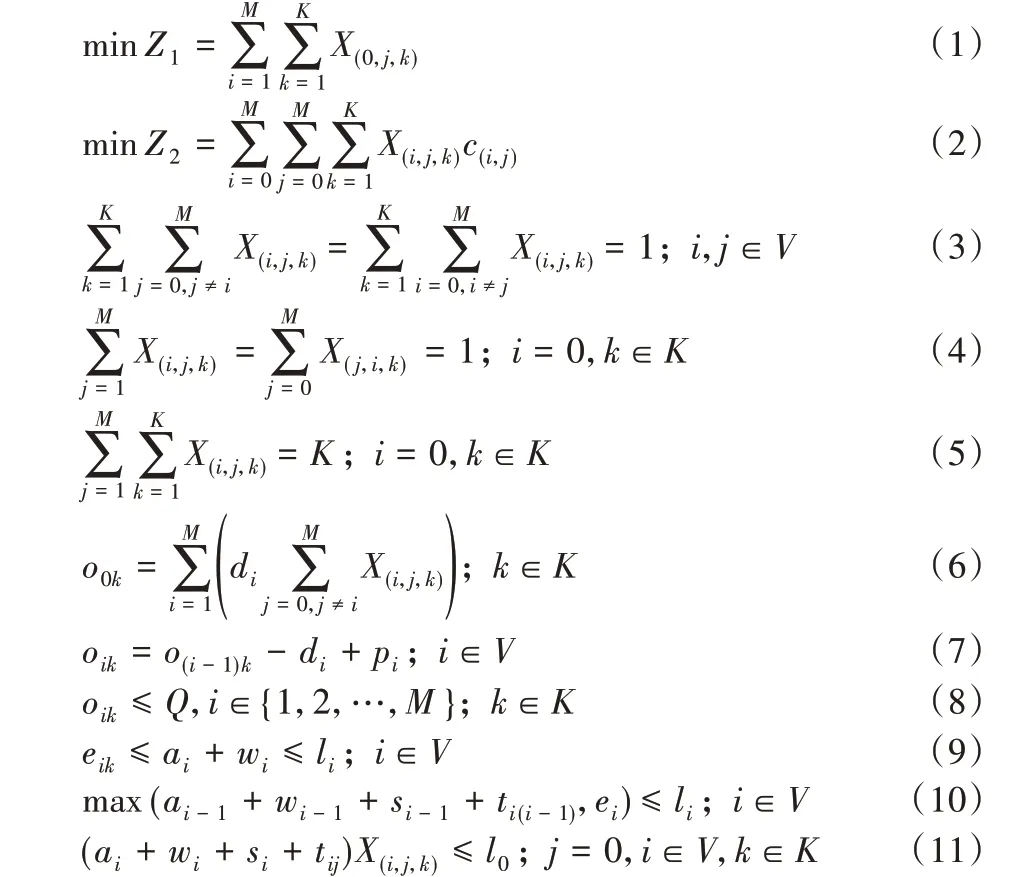
其中:式（1）表示首要目标函数，即车辆数最少；式（2）表示次要目标函数，即车辆行驶的总路径最短；式（3）表示每个客户只被服务一次；式（4）表示车辆需要从配送中心出发，并最终返回配送中心，即起始点和终止点均为配送中心；式（5）表示从配送中心出发的总车辆数为K，即配送车辆数为K；式（6）表示车辆k 在离开配送中心时的装载量，即配送路线上所有客户的配送量之和；式（7）表示车辆k 在离开各个客户时的装载量，等于离开上一个客户时的装载量减去在本客户位置的接收量，再加上本客户的寄送量；式（8）表示车辆在任何时刻，所装载货量都不超过车辆最大载重限制；式（9）表示时间窗符合要求；式（10）表示车辆在对上一位客户服务之后，能及时到达下一个客户所在位置，即上一个客户在车辆到达时刻的基础上，加上等待时间、服务时间和路程耗费时间之和不晚于下一个客户的最晚服务开始时间，同时客户的最早开始服务的时间也不能晚于最晚开始服务的时间；式（11）表示车辆在对最后一位客户服务之后，能及时返回配送中心。

2 求解VRPSPDTW 的模因算法设计

2.1 模因算法主流程

模因算法的运算过程中，首先生成一个初始种群，然后对种群进行进化，进化过程是在上一代个体进行交叉后，对所产生的子代通过邻域搜索等操作进行教育，选出优于父代的个体进行继承。相对于遗传算法，模因算法的方向更加明确，收敛速度和求解效果都有大幅提高［12］。

本文所研究的模因算法包括初始种群生成算法和种群进化算法，首先对初始种群进行生成，然后对种群中的个体逐代进行交叉、修复、教育等操作，实现种群的进化过程，最终得到满意解。本文模因算法总流程见图1。

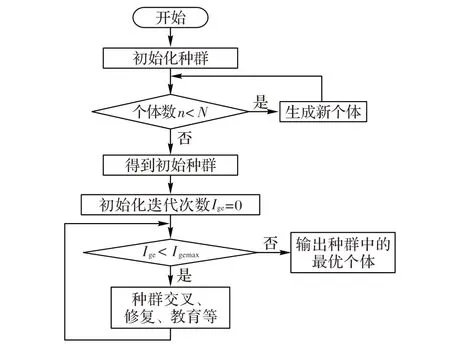
图1 模因算法流程Fig. 1 Flowchart of memetic algorithm

2.2 初始种群生成

首先，采用整数编码［13］的方式对带时间窗的车辆路径问题进行编码，对于一个可行解而言，其中包含多个车辆运输路径，每辆车只对一条路径上的客户进行服务。使用1～m 表示每个客户的编号，1～k 表示每辆车的编号，每条路径使用一个整型向量进行表示，表示一辆车从配送中心出发，对所有客户进行服务后，再次返回到配送中心。每一个解中对应k 条路径。由于每个客户只接受一次服务，因此路径中不存在重复的客户编号。编码结构如图2所示。

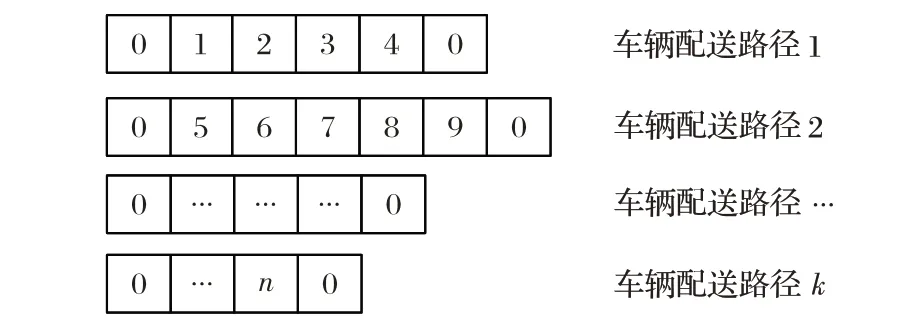
图2 编码结构Fig. 2 Coding structure

初始种群生成时，采用引导弹射搜索（Guided Ejection Search，GES）［11］进行种群生成。首先制定一个基本解，基本解中包含与客户数目相同的数量的车辆，每辆车只对一个客户进行服务，而后逐步减少路线，将每条路线上的客户插入到其他路线中去，直到求出车辆数较小且不违反约束的初始解。通过生成多个初始解，产生一个初始种群。

2.2.1 初始种群生成算法流程

初始种群生成算法流程如图3所示。

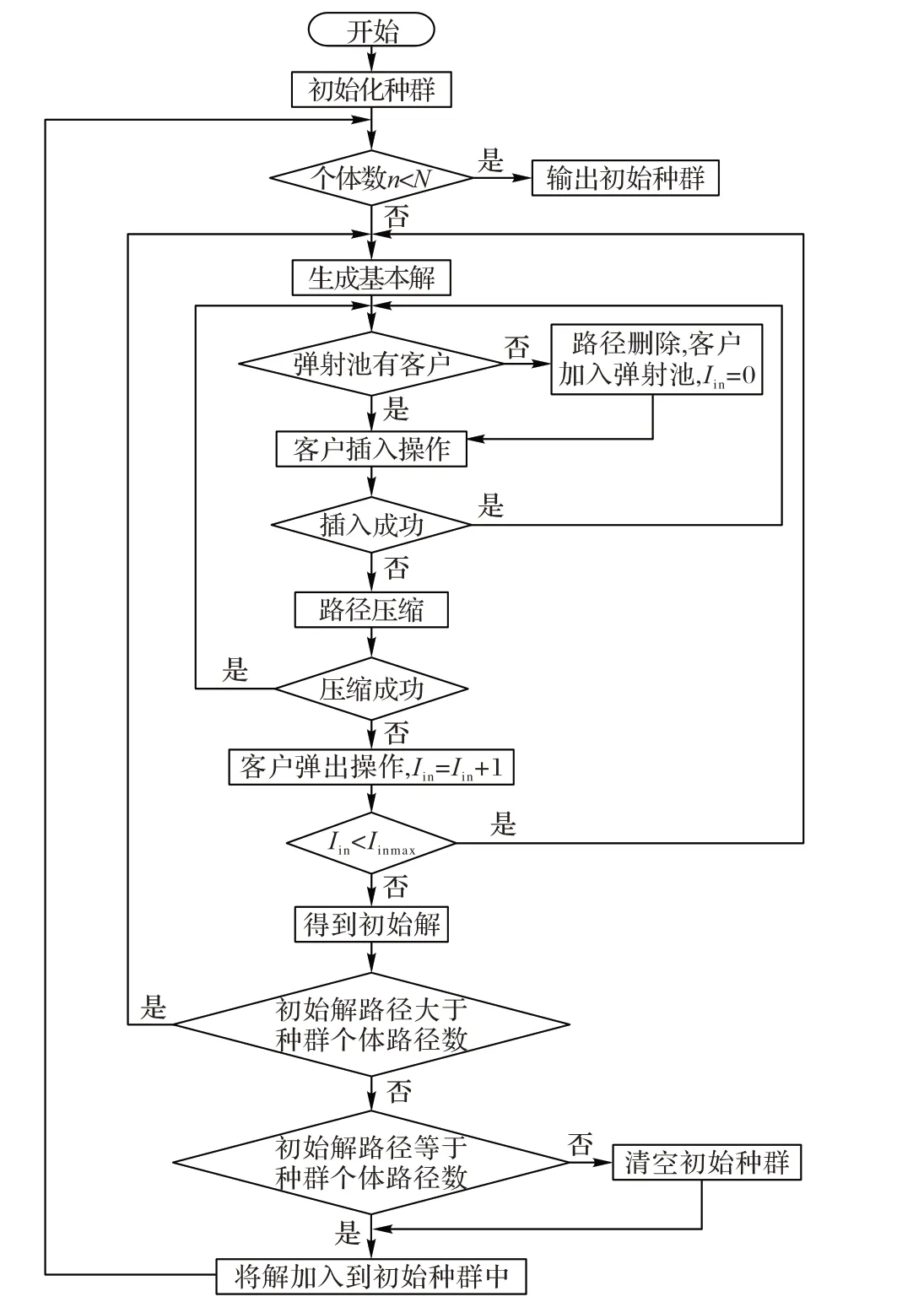
图3 初始种群生成算法流程Fig. 3 Flowchart of initial population generation algorithm

首先设定一个初始种群，种群大小设定为N，初始种群中不包含任何个体；随后通过一系列客户插入、路径压缩、客户弹出等操作生成可行初始解。逐个产生初始解，形成初始种群。

初始种群生成的算法伪码如算法1 所示。依次对一个基本解循环进行客户插入、路径压缩、客户弹出等操作，生成可行初始解。

通过多次生成初始解，逐步形成一个种群规模为N 的初始种群。

2.2.2 制定基本解

首先制定一个基本解，每一个客户对应一条路径，即一辆车只对一个客户进行服务。此时，路径的条数是最多的，与客户数目相同，而后逐一减少路径数目。

2.2.3 路径删除

此时，对具有多条路径的解进行操作。随机选择一条路线，将这条路线删除，并将路线上的所有客户加入到弹射池中。

2.2.4 插入客户

对弹射池中的客户使用后进先出（Last In First Out，LIFO）的策略，从弹射池中选择客户，依次尝试将客户插入到其余路线的每一个位置中进行检验，若存在满足车辆载重和时间窗约束的位置，则将该位置记为可行插入位置。统计所有的可行插入位置，选择一个位置插入客户，形成新的解。

若存在多个可行插入位置，可以采用就近原则进行客户插入，选择将客户插入到对应的插入位置后，对原有路径长度的改变量最小的位置进行插入。

若尝试所有可行插入位置，找不到可行插入位置，则采用路径压缩方法进行处理，对路径进行压缩。

若通过路径压缩方法仍未得到可行解，则采用客户弹出方法，尝试将不可行的客户插入后，弹出其他客户到弹射池中，再进行优化。

若连续多代优化后，弹射池中的客户仍未减少到0，则回到该条路线删除前的状态，重新随机选择一条路线进行删除，若经过Ireadmax次重复删除后，仍无法找到更少路线的解，则以该条路线删除前的解作为满意解，或舍弃该解。

2.2.5 路径压缩

若一个客户无法在不违反车辆载重约束和时间窗约束的情况下，插入到一个可行位置，则尝试将该客户插入到较为合适的位置后，对路线进行邻域搜索，找到不违反车辆载重和时间窗约束的邻域解。

首先对客户插入一个位置后的违反约束函数Fp进行计算，违反约束函数计算公式如式（12）所示。

其中:Fp表示违反约束函数的值；Pc表示违反的载重约束，表示车辆在配送中心和客户位置货物超出车辆载重的和；Ptw表示违反的时间窗约束，即车辆到达客户时间晚于客户要求的最晚到达时间的时间段；α为比例系数。

查找邻域中Fp更小的解，若能找到则在新解的基础上继续查找，直至找到Fp= 0的解，说明路径压缩成功。

若路径压缩失败，则执行客户弹出方法。

2.2.6 客户弹出

若路径压缩失败，则允许将客户插入到一个位置，同时弹出部分客户到弹射池中，制定客户最大弹出数量EJmax，使每次客户最多弹出数目不超过EJmax。

在初始种群生成算法的初始阶段，制定惩罚计数器p[vi]，i ∈{1，2，…，M}，惩罚计数器的值代表每个客户尝试插入或路径压缩失败的次数，即该客户插入到路线后能够成为可行解的难度［11］。选择弹出客户惩罚函数之和最小的客户组合进行弹出，将弹出客户放置到弹射池中，使弹出客户惩罚函数Psum最小。

弹出客户惩罚函数之和计算公式如式（13）所示，表示所有弹出客户的重新插入路线形成可行解的难度之和。此举可以保证在将部分客户弹出之后，该部分客户也较容易找到其他可行位置进行插入。

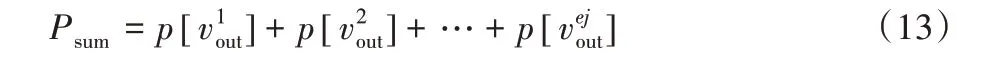
2.2.7 终止条件

对于一个解的求解过程而言，连续Iinmax次客户插入、路径压缩、客户弹出操作后未使弹射池中所有客户全部插入到已有路径中，此时将返回最后一条路径删除前对应的可行解。

设定初始种群大小为N，整个初始种群生成的终止条件设定为生成N个包含相同数量车辆路线的解。若连续Iinmax次客户插入、路径压缩、客户弹出操作失败，则对该解停止优化，并与之前的解进行比较，若车辆路径数目更多，则说明该解不是满意解，舍弃该解；若该解与之前的解路径数目相同，则将该解加入到初始种群中；若该解路径数目更少，则说明该解为更优解，此时清空初始种群中的所有解，将该解加入到初始种群中。

2.3 种群进化

物种进化的基本单位是种群，一个种群经过个体之间的交配可以产生新的个体，模因算法是在普通的遗传算法的基础上，在新个体产生的同时，不仅可以继承父代已接受的文化知识，还能通过教育，学习新的知识，使整个种群获得更快的进化速度。

产生初始种群之后，需要对初始种群的内的个体进行优化，优化目标为产生车辆行驶总路径S 更短的个体，车辆行驶总路径的计算公式见式（14），表示所有配送车辆完成配送任务需行驶的路径总和。

对种群中的个体通过选择、交叉、修复、教育等一系列操作后，形成新的更优秀的种群，作为下一代新种群。

首先对种群个体进行选择，确定新的个体交叉顺序，随后个体之间进行交叉。

对于交叉过程而言，本文采用边界组合交叉进行个体之间的交叉。边界组合交叉（Edge Assembly Crossover，EAX）最初由Nagata 等［14］提出，有向车辆路径问题的边界组合交叉能够更好地继承父代个体的子路径，保持父代个体的基本结构，从而能够继承父代的优秀基因，产生更接近最优解的新个体［15］。

在个体交叉结束后，对个体进行修复、教育，以获得更优的个体。修复、教育的过程采用邻域搜索的方法进行。种群进化算法的终止条件设定为连续Igemax的操作中种群中的最优解未发生改善。种群进化算法流程如图4 所示:描述了一个初始种群个体经过交叉、修复、教育等操作，得到最终解的过程。

种群进化算法伪码如算法2 所示。种群进化过程中，首先对种群随机重排，确定新的交叉顺序，然后对所对应的父代交叉个体进行交叉操作，产生子个体，随后对子个体进行修复、教育。直到连续Igemax代个体未得到改善，输出最终的解。

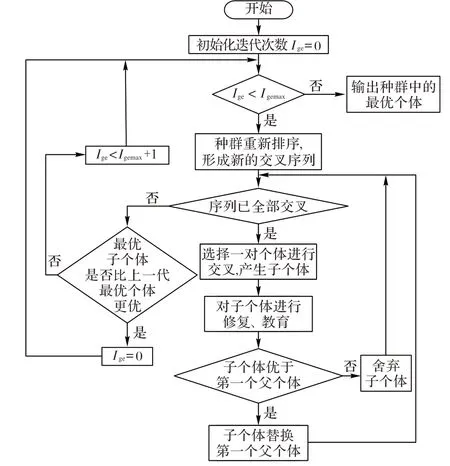
图4 种群进化算法流程Fig. 4 Flowchart of population evolution algorithm

2.3.1 选择

本文的选择过程不对种群中的个体进行舍弃，而是通过对个体进行随机重新排序来改变个体之间的交叉顺序［16］。首先将种群进行随机排列。如原种群经过随机排列后得到种群为{ p1，p2，…，pn}，其中p1，p2，…，pn代表每个种群中的各个可行解，即交叉操作中的父代个体。则父代个体之间的交叉顺序 设 定 为EAX(p1，p2)，EAX(p2，p3)，… ，EAX(pn-1，pn)，EAX(pn，p1)。

2.3.2 交叉

按照所生成的交叉顺序使逐个相邻个体进行交叉。边界组合交叉算法中，首先选择两个父代个体pa和pb，将父代个体进行路线合并，同时删除重复的路径，再对合并后的路径进行拆分，拆分为多个子路径。随后选择一条或多条子路径，替换到第一个父个体pa中，此时部分子路径可能是不经过配送中心的，若存在不经过配送中心的子路径，则对该个体进行路径修复，修复后得到新的子个体。边界组合交叉示意图如图5所示。

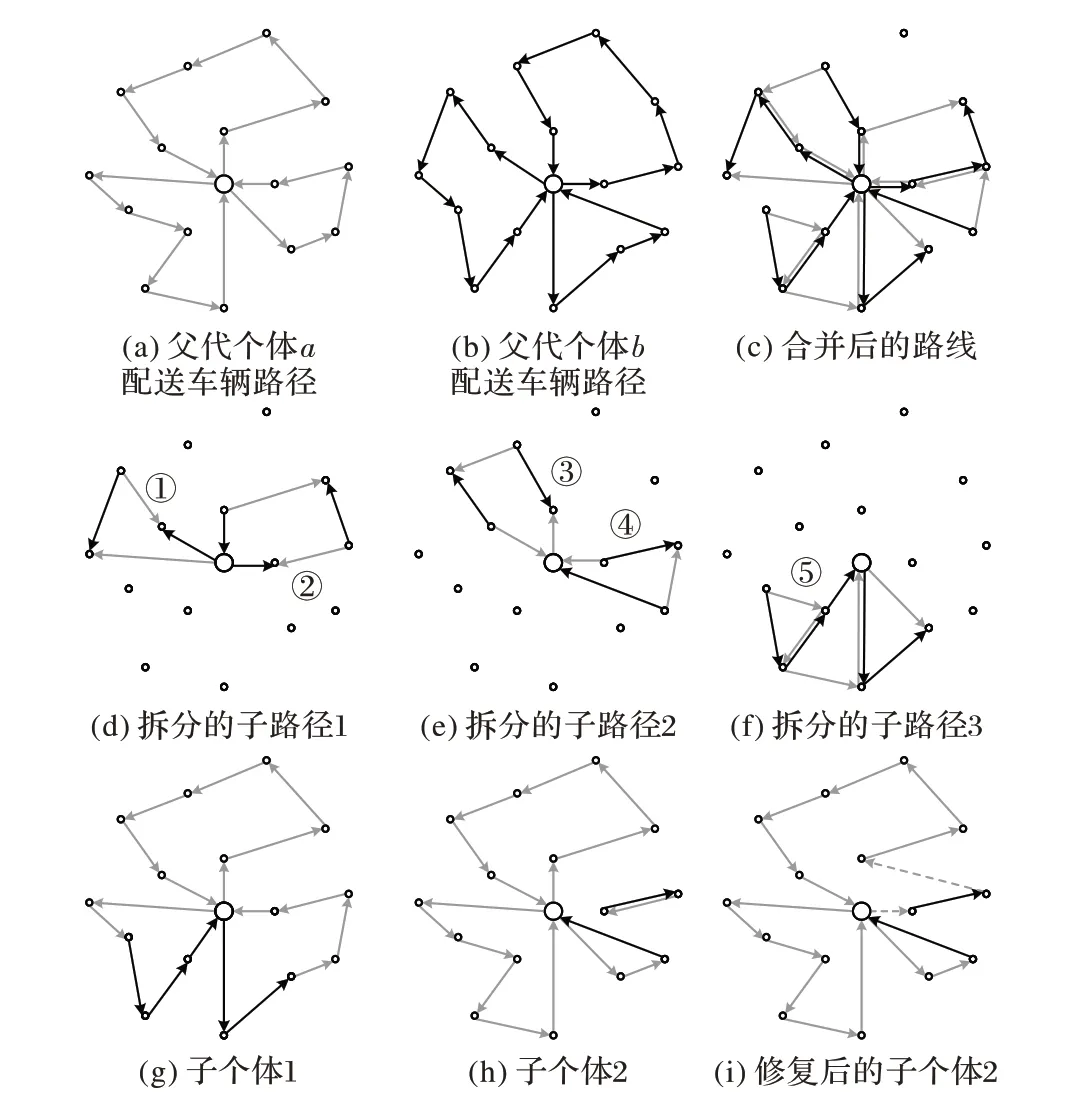
图5 边界组合交叉示例图Fig. 5 EAX sample diagram

2.3.3 修复、教育

边界组合交叉完成后，得到新的子个体，但是新的子个体可能是违反车辆载重约束或时间约束的，即新个体可能是不可行的。此时，需要对子个体进行修复操作［10］，恢复子个体的可行性。在修复的过程中，采用邻域搜索的方法进行解的修复，邻域搜索采用In-relocate 算子（图6（a））、Out-relocate 算子（图6（b））、In-exchange 算子（图6（c））、Out-exchange 算子（图6（d））进行搜索。对当前解对应的邻域进行搜索，查找邻域中违反约束函数Fp更小的个体，若找到Fp更小的个体，则在新个体的基础上继续进行搜索，直至找到违反约束函数Fp= 0的个体或找不到具有更小违反约束函数Fp的个体。使用新形成的解替换之前的子个体，形成新的子个体。若无法找到不违反约束的解，则将该子个体舍弃。

修复完成后，若得到的解是可行解，需要对子个体进行教育［10］。教育的目的是为得到更优的个体，即车辆行驶总路径S 更短的解。教育的过程中，仍然是采用邻域搜索的方法，除上述四种算子之外，还采用2-opt*算子［17］（图6（e））进行搜索。对当前解对应的邻域进行搜索，查找邻域中车辆行驶总路径S更短的个体，若找到S更小的个体，将在该个体的基础上，重新对新个体的邻域进行搜索，直到邻域中找不到车辆行驶总路径S更短的个体。将新形成的解作为教育后的子个体。

每次交叉完成后，对子个体pc经过修复、教育。此时，若新的子个体pc不违反车辆载重约束和时间窗约束，并且pc的车辆行驶总路径小于边界组合交叉的第一个父个体pa的行驶总路径，则使用pc替换掉第一个父个体，直至所有交叉进行完成。

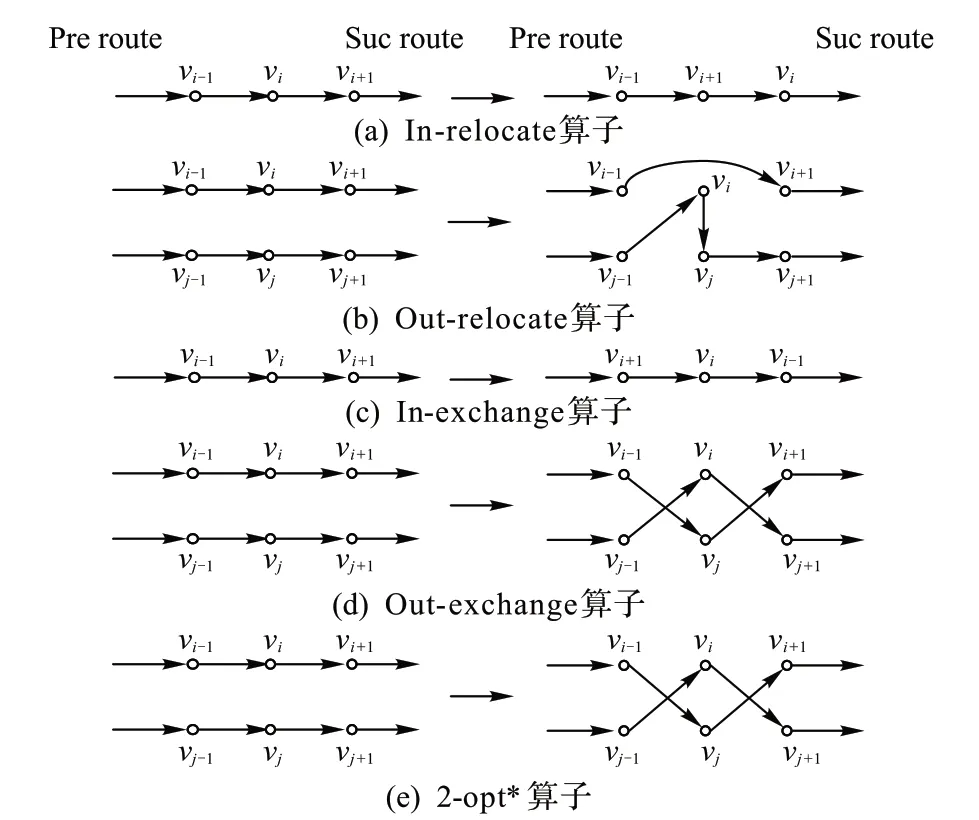
图6 算子示意图Fig. 6 Schematic diagram of operators

2.3.4 终止条件

终止条件设定为连续Igemax的操作中种群中的最优解未得到改善。进化终止后，选取种群中车辆行驶总路径最短的个体作为最终解。

3 算例实验与分析

3.1 测试环境和参数确定

本文模因算法使用Java 语言进行编写，算法运行环境采用Intel Core i5-3230M CPU@2.60 GHz（8.00 GB 内 存），Windows 10 x64操作系统。

由于本文模因算法求解过程分两阶段进行，因此初始种群生成算法和种群进化算法的参数可以分别进行确定。

初始种群生成过程中，需要确定的参数包括:客户最大弹出数量EJmax；客户弹出失败后重复删除次数Ireadmax；最大连续迭代次数Iinmax。以计算得到满足标准车辆数的可行解所耗费的时间作为评价因素，所耗时间越少，说明得到初始种群速度越快，以重复三次实验的平均值作为评价指标。初始种群生成中的参数确定包含3 个参数，采用三因子三水平实验，选用正交表L9(34)进行实验。确定初始种群生成的过程中，最优参数组合为EJmax=4，Ireadmax=10，Iinmax=10。

种群进化过程中需要确定的参数包括种群规模N；连续多代未发生优化的终止迭代次数Igemax。以计算结合和程序运行实验为评价因素，实验需要确定的参数较少，采取固定一个参数，调整另一个参数的方法对参数进行确定实验。确定种群进化过程参数设置为N=40，Igemax=50。

算例实验过程中，为保证算法的准确性，对每个算例进行3次实验，取3次的最优值作为实验结果。

3.2 小规模客户算例实验

为测试本文模因算法计算小规模客户带时间窗的同时取送货问题的性能，本文采用Wang 等［3］的小规模标准算例进行实验。小规模标准算例包括10 个客户规模、25 个客户规模、50 个客户规模的算例各三个。在满足车辆载重约束和时间窗约束的条件下进行实验，将实验结果与Wang 等［3］设计的遗传 算 法（GA）、Wang 等［6］设 计 的 并 行 模 拟 退 火（parallel-Simulated Annealing，p-SA）算法、王超等［7］设计的离散布谷鸟搜索（Discrete Cuckoo Search，DCS）算法取得的最优实验结果进行比较。

实验对比结果如表1 所示，四种算法实验结果中，NV 和TD 分别表示配送车辆数和配送总路径，加粗的结果代表本文算法取得的最优解。分析发现，本文模因算法可以求得全部9 个小顾客规模算例的已知最优车辆和最短路径，验证了本算法在求解小规模客户带时间窗的同时取送货问题的有效性。

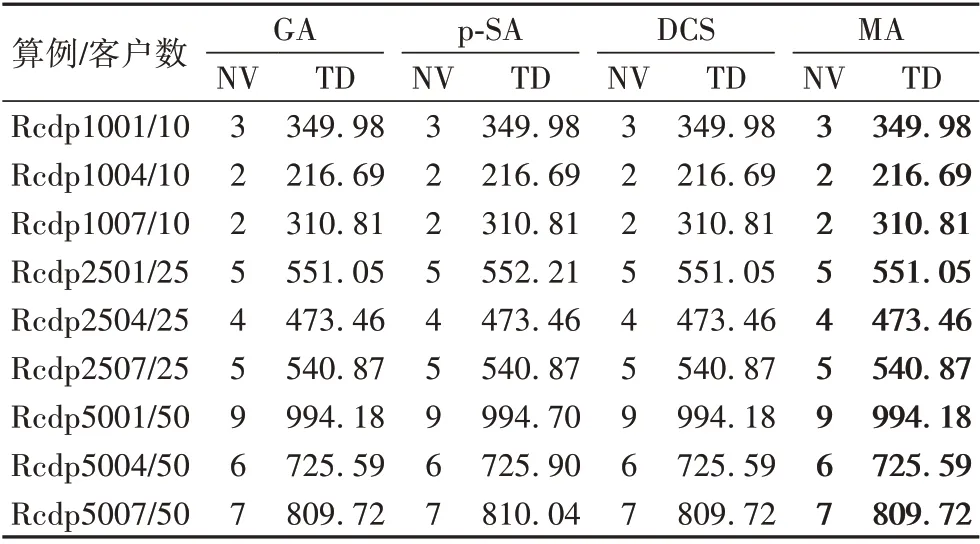
表1 小规模客户算例实验结果对比Tab. 1 Comparison of experimental results of small-scale customer examples

3.3 标准规模客户算例实验

为测试本文模因算法计算标准规模客户带时间窗的同时取送货问题的性能，本文采用Wang 等［3］的标准规模算例进行实验。随机选取10 个算例进行实验，每个算例包括100 个客户。

在满足车辆载重约束和时间窗约束的条件下进行实验，将实验结果与GA［3］、p-SA［6］、DCS［7］取得的最优实验结果进行比较。实验对比结果如表2所示，4种算法实验结果中，NV 和TD 分别表示配送车辆数和配送总路径，加粗的结果代表本算法更新或取得的最优解。

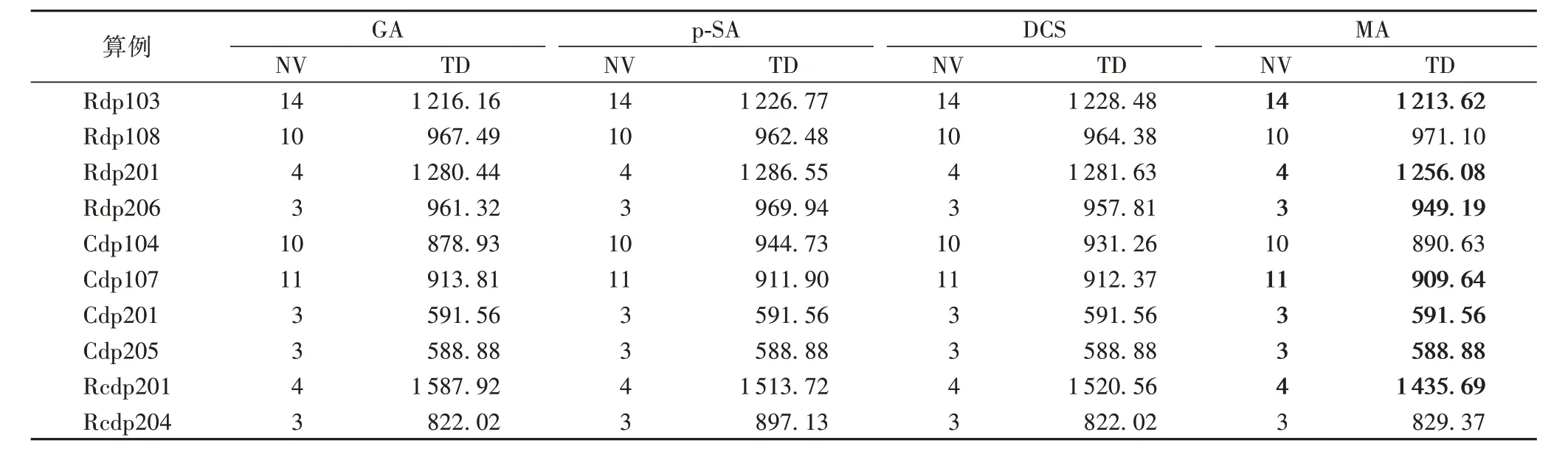
表2 标准规模客户算例实验结果对比Tab. 2 Comparison of experimental results of standard-scale customer examples

对结果进行分析，发现在10个标准算例中，算例Rdp103、Rdp201、Rdp206、Cdp107、Rcdp201 共5 个算例更新了当前最优解；算例Cdp201、Cdp205 共2 个算例取得了与当前最优解相同的结果；仅有1 个算例未取得比其余三种算法更优的结果。

为更直观地展示本文实验结果，选取Rdp103算例实验结果生成配送路线图，路线如图7 所示。由于本实验车辆配送时间完全按照客户要求的时间窗进行配送，并且严格满足车辆的载重要求，因此路线中会出现部分交叉的情况，但路线图整体取得了较好的结果。

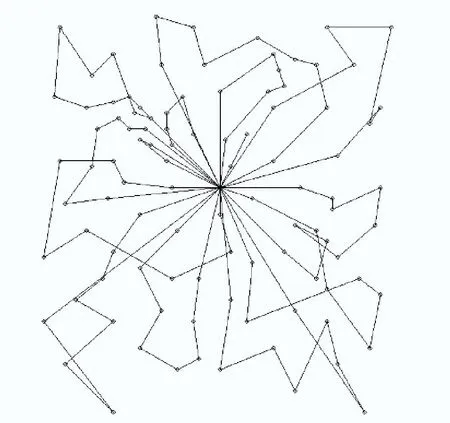
图7 Rdp103算例配送路线Fig. 7 Delivery route of Rdp103 example

本文采取通过建立合适的数学模型，采用基于引导弹射搜索和边界组合交叉的模因算法，使用弹射池方法生成初始解，大幅度提升了初始解的质量，同时在种群进化过程中，采用EAX 对父代个体进行交叉，保留了父代个体的优良基因，采用多种算子对种群中的解进行修复、教育，提升了邻域搜索的广度。算例实验中，对于更新了当前最优解的5 个算例结果而言，其中Rcdp201 算例对当前最优解有超过5%的提升，Rdp201 对当前最优解有约2%的提升，Rdp206 对当前最优解有超过1%的提升。本文算法更新或达到最优解的算例占测试算例的70%，其中50%的算例更新了最优解，充分说明了本文模因算法在求解标准规模客户带时间窗的同时取送货问题的有效性。

4 结语

为迎合现代物流发展，解决带时间窗的同时取送货车辆路径问题，本文建立了相应的车辆路径问题模型，并使用基于引导弹射搜索和边界组合交叉的模因算法对问题进行求解。在算法求解过程中分两阶段进行求解，首先使用GES 方法生成初始种群，随后在种群进化的过程中采用EAX 交叉产生子代，同时使用多种邻域结构对子代进行修复教育，以得到更合理的路径。使用本文模因算法对Wang 等［3］提出的标准算例进行算例实验，得到了较好的求解结果，验证了本文模因算法的有效性。

现代物流的发展不仅会面临同时取送货问题，还会面临诸如搬家服务之类的带时间窗的取送货车辆路径问题，接下来的研究方向是对两类问题进行整合求解，设计适应范围更广的算法。