基于Web的动态几何软件领域模型及其应用

管 皓，秦小林*，饶永生，曹 晟

（1. 中国科学院大学计算机科学与技术学院，北京100049； 2. 中国科学院成都计算机应用研究所，成都610041；3. 广州大学计算科技研究院，广州510006； 4. 电子科技大学信息与软件工程学院，成都610054）

（∗通信作者电子邮箱qinxl2001@126.com）

0 引言

动态几何软件用于在计算机上交互地绘制几何图形，构造约束关系。在计算机屏幕上做出的几何图形，如果在变化和运动过程中能保持其几何关系（如线段的长度相等，相互垂直、平行等）不变，就叫动态几何图形。有关动态几何图形的理论和应用的学科，就是“动态几何”［1］。在数学教学过程中运用诸如动态几何软件的信息技术，可构建形象灵活的可操作工作环境，从而提高思考层次，获得更好解决问题的技能［2］。有相关实验表明在学习几何知识时，与动态几何软件进行交互探索有利于降低学生学习过程中的认知负荷，提升学习效果［3］。

Cabri 是最早出现的动态几何软件。20 世纪80 年代在美国国家科学基金支持下，设计并研发了几何画板（The Geometer's Sketchpad，GSP）。这两款动态几何软件对数学教育提供了有力支持，其教育价值很快得到了世界各国的肯定。尔后，欧美等发达国家研发了数十种动态几何软件［4］，代表性的软件包括:GeoGebra、Cinderella 等。从20 世纪90 年代开始，国内学者为我国基础数学教育研发了超级画板（Supper SketchPad，SSP），对动态几何软件的设计和实现也做了大量工作［5-8］，其教育价值也得到了充分的挖掘和研究，对于推动学科信息化起到了重要作用。

动态几何软件经过30 年多的发展，研究重点大多在其数学及算法基础理论［9-10］、交互设计［11］、应用实证［12-13］等方面。至今尚未从领域工程角度对其进行讨论设计，导致上述得到的模型不能完整有效地反映动态几何领域，使得大多的动态几何软件局限于特定的操作系统及终端设备。复用是软件开发过程中重要的原则，然而缺乏对领域内可复用的抽象描述，往往只能在构建级或代码级等较低层次进行，无法保证用户概念模型、设计模型与系统实现的统一。亟须使用相应的软件方法对动态几何类软件进行分析设计，对其合理地分层以支持可持续稳定演进，以适应不断更新的技术环境及应用场景。从基础图形中，再不断往下派生出由不同几何约束定义的子类，子类包含了几何约束信息及其求解算法，例如中点、两条直线的交点等。当鼠标拖动自由对象后，通过遍历得到与之相关联的对象，并放进需要更新的列表中，再依次对列表中的对象进行计算更新。该过程看起来很直观，然而实现却颇具挑战，文献［23］对此做了更为详尽的描述。

德国著名动态几何软件Cinderella 的作者Kortenkamp［24］抛弃了上述经典的继承体系，在其博士论文中提出另一种面向对象的设计方法，核心模型如图1所示。

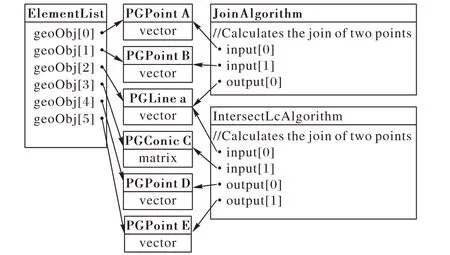
图1 Cinderella 核心模型设计Fig. 1 Core model design of Cinderella

1 相关工作

如何有效利用各种Web 技术来辅助教育教学已成为了重点研究方向［14］。基于Web 技术的动态几何软件具有很多技术上的优势和教育教学上的价值。早期Web 技术运行效率较低，无法满足动态几何密集计算的性能要求，也无法处理多媒体图形图像数据，需要借助Web 扩展技术或是插件。Richter-Gebert 等［15-16］研 发 的Cinderella 在 早 期 就 支 持 导 出Web 页面可交互的动态数学内容，之后利用Java Applet 研发了交互性更好的平台，适用于在支持Java Applet 的特定浏览器上运行。 GSP 也利用 Java Applet 研发出了JavaSketchpad［17］，支持在Web 页面上演示动态数学内容。另一种较为通用解决的方案是利用可缩放矢量图形（Scalable Vector Graphics，SVG）技术，Wang 等［18］研制的GeoSVG 就利用SVG 技术在浏览器上实现了动态绘图，并支持用户创建个人的文件空间；Ehmann 等［19］利用SVG 研发了JSXGraph 动态几何库，基于该库开发的Sketchometry，支持在触碰设备上利用手势进行绘图，得到较为广泛的应用。然而Java Applet 无法满足在所有浏览器上运行，特别是在日益普及的各种手持设备，Oracle 公司也宣布不再维护该技术。SVG 采用XML 格式描述图形，可利用JavaScript 语言操作文档对象模型（Document Object Model，DOM）来操作图形，但DOM 的操作性能较低，无法实现复杂的图形。随着HTML5 标准的普及，现代浏览器都已经支持更为高效的图形接口Canvas，同时支持二维及三维图形，其中三维图形底层技术WebGL 可借助高效的GPU，达到十分可观的性能。GeoGebra［20］利用Canvas，实现了真正意义的跨平台、在现代浏览器上都能无缝运行的动态几何软件；Von Gagern 等［21］研发的CindyJS 是在Cinderella的基础之上，利用WebGL 技术实现的一款高效的动态几何库。

在已有的研究中，虽然没有运用到领域工程的相关方法对动态几何软件进行领域建模，但也从数据结构方面做了一定工作，部分反映了其领域知识。在现有动态几何软件中，数据结构大多都采用单一经典的面向对象继承体系［22］。

所有的几何对象都从基类GeometryElement 继承派生而来。该基类包含了公有的方法和属性，如颜色、标签、显示、隐藏等。由该类直接派生而来的有Point、Line、Conic 等，包含相应的几何属性用以表示不同类型的基础几何图形:例如Point包含了坐标信息，Conic 包含了圆锥曲线的一般方程系数等。

从图1 中可以看出两种主要的对象:Element 与Algorithm。其中:Element 经过派生细化为PGPoint、PGLine、PGConic 等少数几种基础几何图形；Algorithm 中包含多个输入（input）及一个或多个输出（output）对象，描述了由输入图形到输出图形某种约束关系。相对于经典的继承体系，将Algorithm 复合关联至Element 中具有更高的灵活性，支持方便地实现修改某个图形的定义。另一个好处是在性能上会有一定提升，例如InsesectLCAlgorithm 类描述了直线与圆锥曲线的交点这样的几何约束，该约束对应了两个output 几何图形（PGPoint）。直线与圆锥曲线的交点至多有两个，在更新两个交点时实际上只需一次运算，这样的设计有利于提高计算结果的重用，提高软件的运行效率、增强稳定性。

2 基于Web的动态几何软件领域建模

Arango［25］提出领域的内聚性和稳定性是获取和表示领域内可复用信息的前提。对于相关软件系统的共性进行系统分析和利用是成功的软件复用的基础。目前已经出现了多种领域工程方法，适用于不同的目标、产品和过程。Kang 等［26］提出的面向特征的领域分析（Feature-Oriented Domain Analysis，FODA）方法引入特征模型用于抽象描述需求。其他诸如FOOM［27］、产品线分析（Product Line Analysis，PLA）［28］等方法，也都利用多种模型对领域内应用的共性和特性进行描述。由王千祥等［29］提出的“青鸟领域工程方法”，是一种面向对象的领域工程方法，明确规定了领域工程中各个阶段的活动，并对每个阶段给出操作指南。

利用领域工程的相关方法，通过特征描述、领域术语词典、可复用构件等技术，将问题域和方法域的描述有机地结合在一起［30］，在保持领域内聚性和稳定性的前提下，使系统能够快速而准确地反映外部环境（如用户需求、展现技术、交互方式等）的变化，保证实现系统的可用性。具体表现在以下几个方面:划分问题空间，降低单个系统的复杂度；建立统一的业务语言即术语库，用于理解和消化业务知识，避免出现理解误差；对系统进行合理的分层，隔离业务逻辑及展现层，使得系统可在保持业务逻辑不变的前提下满足不同的设备界面布局及交互手段。

领域模型的建立分为3 个阶段:用于确定领域边界的领域分析、用于领域内问题描述的领域设计以及提供方法域上层结构描述的体系结构建模。

下面以“网络画板（NetPad）”为例，对基于Web 的动态几何软件进行领域建模。

2.1 领域分析

领域分析用于确定领域边界，具体涉及如何划分和定义问题空间。传统桌面应用一般以单体应用的形式研发、下载及安装。与此不同，基于Web 的动态几何软件无需下载安装，所创建的资源作品也都存储在云端，随时随地都可使用分享，给用户带来了极大的便利。同时也给设计跟实现带来更多挑战，就系统复杂度而言比单体应用要复杂得多，因此在做领域设计之前，有必要对该系统涉及到的问题空间进行合理的划分隔离复杂度，对不同的问题空间分而治之，而问题空间对应的领域设计即是对该问题空间的解决方案。经过分析识别并划分出最基本的上下文边界:1）身份与访问领域。涉及到用户访问时，对用户进行鉴权及身份识别，管理相关的访问权限等问题，具有一定的通用性，因此也往往被识别为通用域，作为系统重要的基础设施。2）资源交互领域。涉及到用户使用动态几何软件制作的作品相关操作，例如作品如何存储、分类管理、检索、设置其他用户对其作品的使用权限等。其涉及的问题空间并非是动态几何软件核心问题，但却是整个系统十分必要的业务支撑，领域中被识别为支撑域。3）动态数学领域:动态几何软件为组态软件，用户通过类似“搭积木”的简单方式来完成自己所需要的软件功能，而不需要编写计算机程序，有时候也称为“二次开发”，组态软件就称为“二次开发平台”。利用该软件提供的工作环境，允许用户使用软件提供的基础功能，或是编程接口自由组织并进行创作几何作图、变换等动态数学内容。该上下文对应的问题空间主要涉及到如何组织动态几何的相关元素、几何约束、变换等。在该系统中，应被识别是核心域，是整个系统的核心价值所在。

2.2 领域模型设计

Norman［31］曾提出了用以描述“设计概念模型”与“用户理解模型”之间的关系的框架，在理论上，两个模型之间应能够完全相互映射。领域设计是领域工程的第2 阶段，此阶段的主要目的是，针对领域分析获得的领域边界及问题空间的认识开发出相应的设计模型，并显式地表示出来，认识并对其进行合理的领域设计是关键问题所在。

对于动态几何软件而言，其核心需求是实现二维或三维的动态图形、解析几何及函数曲线的绘制及变换。无论以什么样的形式展现在用户面前，其几何元素及其约束关系涉及到领域模型都适用，具有在领域知识层面的复用性。动态几何软件都具有“拖动模式”（Drag Mode）:即拖动自由元素，受约束的元素在保持其几何约束的前提下自动求解并调整其几何属性。其中元素（Element）领域中的核心概念，对于建立领域知识十分必要。

经过上述分析，设计了如图2所示的模型设计。

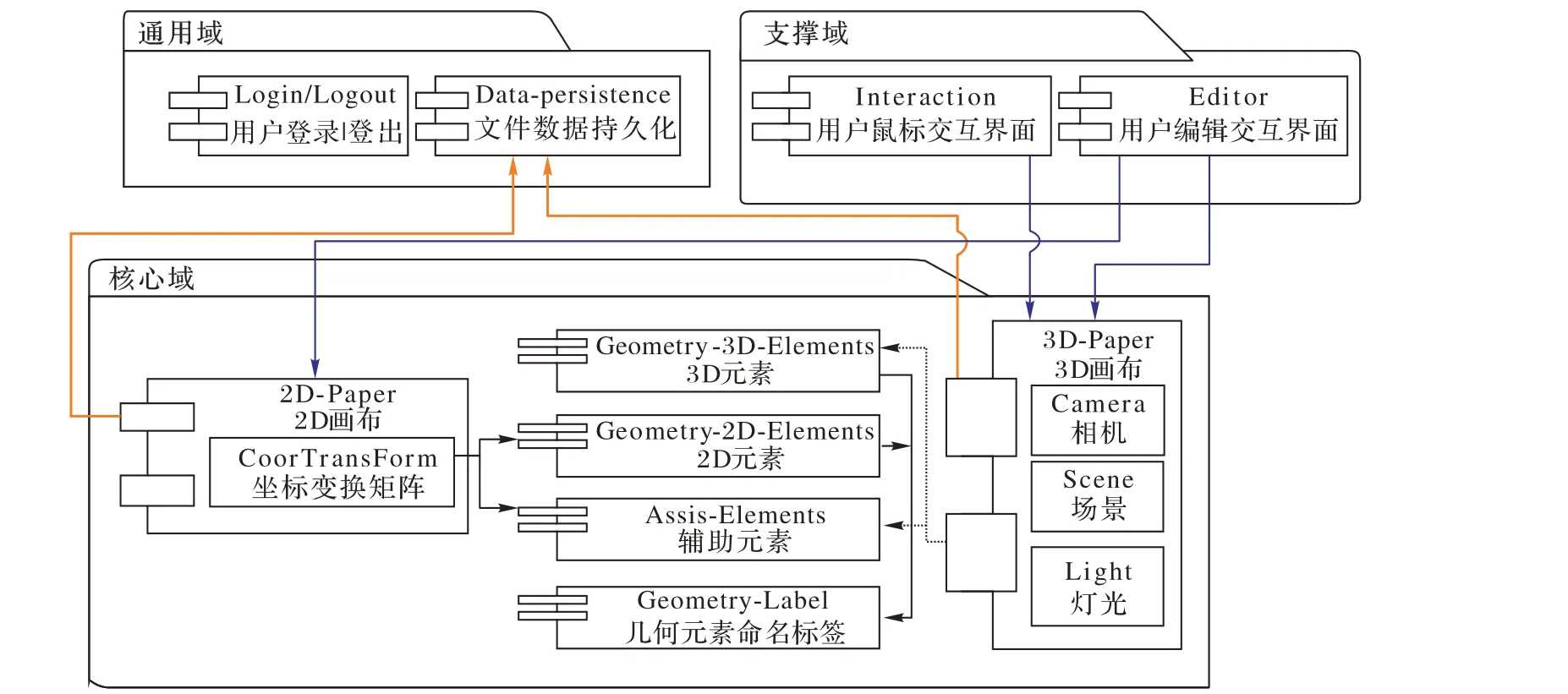
图2 领域设计Fig. 2 Domain design

其 中 元 素（Element），包 括Geometry_3D_Elements、Geometry_2D_Elements、Assit_Elements，是 聚 合 约 束 关 系（Constrain）和约束对象（ConstrainObject）的聚合根，其主要目的是便于动态修改元素输出的几何图元类型，当几何图形在退化情况下仍能够正确定义，包含正确的几何性质。ConstrainObject是该元素确定的具体图形类型，该对象可细化为不同类型的几何图元。例如在二维中常见的几何图元为:点、直线、圆、圆锥曲线、多边形、曲线等，在三维中常见的几何图元为点、直线、圆、平面、曲线、曲面及球、多面体等实体。Constrain 则确定了具体的几何或代数约束，涉及到约束元素、相关参数、被约束关系及约束关系具体的计算规则等。约束关系也是动态几何软件领域模型中高度抽象的对象，适用于二维或三维的动态几何模型。跟几何图元类型较少不同，约束关系具有更多样性，例如在约束点的约束关系有:两点确定的中点、线段确定的中点、三点确定的三角形的中心、圆确定的圆心，等等。设计约束关系时，应特别注意到前面所述的几何中临界位置时遇到的退化情况，诸如三点确定的圆当三点共线时圆即退化为直线；圆锥曲线在也可能退化为两条直线。

当自由点经过通过或变量驱动发生变化后，系统必须将与之依赖的几何元素的约束关系进行重新计算，在具体计算某个元素时应根据其父元素的状态动态地选择计算方法，并生成新的ConstainObject。这一过程反映了动态几何软件的核心流程。

2.3 体系结构建模

创建出能够处理复杂任务的软件，需要将不同的关注点分开考虑，使设计中的每个部分都得到单独的关注。在分离的同时，还需要维持系统内部复杂的交互关系。然而分割软件系统有各种各样的方式，普遍都采用分层架构，分层的价值在于每一层代表软件中的某特定方面，这种限制使得每个方面都更具有内聚性，便于理解。

随着技术的发展，应用于教学的各种终端设备屏幕尺寸不一（电子白板、一体机、平板电脑、智能手机等），鼠标、键盘、触屏、视点等输入设备层出不穷。如何结合不同设备特点，有针对性地设计界面展现及交互方式，实现界面与领域知识的解耦，是体系建模重要目的之一。从应用角度而言，老师用于演示与学生自主探究，也对软件的交互方式提出了不同需求。基于前面的领域分析、领域模型设计，结合软件分层的相关理论与技术，本文设计了如图3所示的分层体系结构。

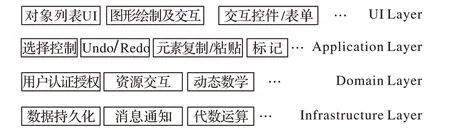
图3 分层体系结构Fig. 3 Hierarchical architecture

1）UI 层（UI Layer）。负责对几何图形的绘制，包括二维与三维图形；同时还应针对不同的设备（如PC、手机及平板）对界面进行合理的布局，兼容不同的交互方式（鼠标、触屏手势、输入笔甚至VR 可穿戴设备）。该层次的重要性主要体现在用户交互的便利、直观性，旨在给用户呈现简洁美观的交互界面及合理便利的交互方式。

2）应用层（Application Layer）。在动态几何软件中主要涉及到带约束元素的创建、修改、删除、复制粘贴以及这些操作的撤销重做；标记图形变换中心、向量及对称轴等动态几何中常用的功能，是为了让变换操作更为便捷并不涉及到动态数学业务规则，因此也是属于应用层。

3）领域层（Domain Layer）。负责表达业务概念、业务状态信息及业务规则。领域层中的动态数学维护了动态几何图形及其约束关系，确定了元素的更新机制。

4）基础设施层（Infrastructure）。为上面各层提供通用技术能力，为应用层传递消息，为领域层提供持久化机制等。因此基础设施层主要包含了数据持久化、消息通信等基础模块，其他诸如代数运算等，为动态几核心域提供了数值或符号运算的支持。

上述的分层方法是基于领域驱动设计的分层的经典架构，其中上层依赖于下层，其关系为直接调用；下层为上层提供必要的服务，下层无需感知上层的存在，但可以通过消息或事件等方式与上层进行间接通信。每层内的模块划分是基于这样两个依据:1）面对变化进行解耦；2）基于关注点进行内聚。

通过纵向与横向两个维度对复杂软件进行解耦，可在保证稳定的前提下，持续演进。

面对不同的终端设备，为适应操作习惯和界面布局，可能需要有不同的UI层，此时仅需要调用下层提供的接口或是监听下层的事件，对UI层进行独立开发。

面对不同的应用场景时，也需要对功能进行合理的拆分或重组。例如在某些场景下，仅需要代数功能、2D 作图功能或是3D 作图，等等。通过对层次内部的模块的抽离，剥离出不必要的模块，再重新组合编译，即可实现具有在特定领域的完整功能可独立运行的软件。

3 应用实例与实验

基于该领域模型，研发的基于Web 技术的动态几何软件“网络画板（Netpad）”具有多终端、高效及稳定等特点，并有效保证了该软件持续稳定的地演进。

3.1 支持在多终端中运行

领域模型给出的分层结构将核心领域与UI 展现隔离开来，可以对不同尺寸设备上的展现及交互方式做针对性的设计。在PC、平板电脑屏幕空间足够的环境下可作为创作空间，提供完整的功能组件；而在智能手机上，则以预览体验为主，提供有限的交互。在使用鼠标交互为主的场景中，实现鼠标双击、单击、右键配合键盘操作习惯；而在触屏设备上则又充分利用了手势的便利性。图4 分别给出了在PC 与智能手机环境下的布局与交互示例。

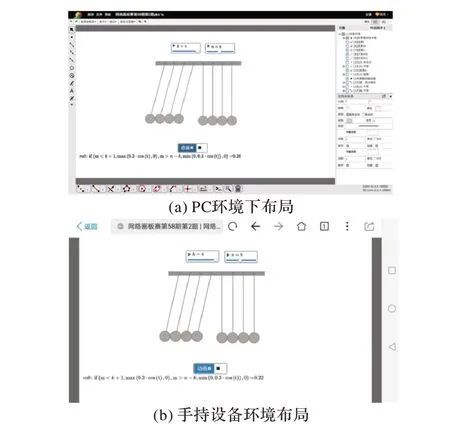
图4 多终端的布局与交互Fig.4 Multi-terminal layout and interaction

3.2 统一实现二维及三维动态几何

二维与三维的动态几何图形，具有相同的几何约束特点，其领域知识和模型具有统一性，主要区别在于元素的具体定义、几何约束的实际算法及图形绘制技术。在领域模型中，很容易复用现有的领域知识，扩展出三维几何图形定义及添加相应的约束算法。而体系建模给出的合理分层，将数据模型与UI层隔离，降低了耦合度。可在不影响已有的二维动态几何功能的前提下，快速迭代和开发出三维的UI 层，实现完整的三维动态几何工作环境。图5 给出了基于该领域模型创建的三维动态几何的工作环境，图6 给出了使用该三维工作环境创建的各种有趣的案例。

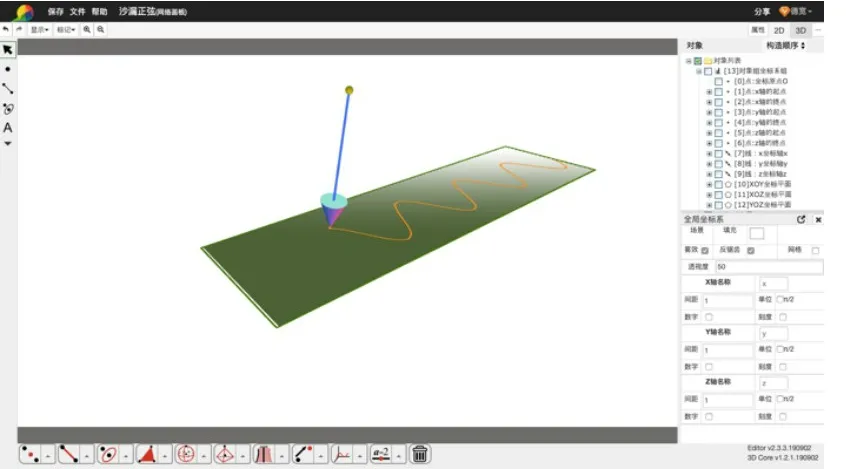
图5 三维动态几何工作环境Fig. 5 3D dynamic geometry working environment

图6 三维动态几何案例举例Fig.6 Examples of 3D dynamic geometry

3.3 探究临界点

动态几何系统一个重要的应用场景是探究，通过移动自由元素探究各种不同情况下的一般规律或是特殊的临界点。为探究在何时三角形的垂心、外心、内心共线，绘制任意三角形，并分别构造出三角形的垂心、外心和内心。

通过拖动或是动画按钮可方便地将一般三角形ABC变成特殊的等腰三角形，可看到此时EFD 三点共线，且由EFD 构造的三点圆退化为一条直线。

图7 分别展示Netpad、SSP、Cinderella 对于上述构图探究案例的实验对比，包含起始实例，中间关键帧实例及终止实例。其中SSP 在三点共线时，圆EFD 无法定义；Cinderella 在三点共线时，圆EFD 出现了定义错误，呈现出一条水平直线。通过对比实验，可看出利用本文提出的模型，能有效展示在临界点时三点圆退化的情形，更好地呈现直线与圆的几何性质的统一，有利于教学的探究和演示。

图7 探究等腰三角形的垂心、外心、内心共线Fig.7 Study of collineation of orthocenter，circumcenter and incenter of isosceles triangle

4 结语

领域模型的建立是不断补充，不断求精逐步演进的过程。在未来工作中，将继续应对外部使用场景的变化、技术设备的更新，寻求更加接近事物本质的领域模型。当前已经完整实现了二维及三维动态几何，包括平面几何、解析几何及函数曲线的动态绘制及其变换，支持在使用鼠标、触屏手势等交互，广泛应用于数学、物理等学科教学过程中。截至目前“网络画板”注册用户超过300 000，为几十所中小学及各大教育云平台提供服务，已进入常规的课堂教学活动。如何结合虚拟现实、增强现实等技术，将动态几何与沉浸式的穿戴设备结合起来，进一步辅助教育教学是后续重点研究的方向。