玻纤增强柔性管抗外压性能研究

刘 畅，张宗政，李淳芳，林珊颖，白 勇,

（1. 南方科技大学 深圳海洋油气钻采装备与管缆工程实验室，广东 深圳 518000；2. 深圳市欧佩亚海洋工程有限公司，广东 深圳 518000；3. 北京数码易知科技发展有限责任公司，北京100010）

0 引 言

玻纤增强柔性管是一种新型非金属增强复合管，主要由内衬层、增强层和外保护层构成，其中：内衬层和外保护层通常采用热塑性高分子材料；增强层是由多层纤维带复合材料以一定的角度交错缠绕而成的复杂结构层。玻纤增强柔性复合管作为油气管道有很多优势，如易于安装和抗腐蚀能力强等，将其推广到海洋和陆地有关领域中应用有很大意义。但是，玻纤增强柔性管开发时间很短。

本文对外压载荷下玻纤增强柔性管力学性能进行研究，采用有限元软件ABAQUS建立外压模型，并对玻纤增强柔性管进行外压试验，将管道可承受的最大外压数值分析结果分别与有限元分析结果和试验结果相对比，发现二者的吻合度很高，表明文中的理论公式可用来计算玻纤增强柔性管可承受的最大外压值，指导工程实践。目前只对玻纤增强柔性管的制造工艺和安装方式等内容进行初步研究，有关其力学性能的研究还处在起步阶段[1-2]。

1 数值分析

1.1 基本假设

玻纤增强柔性管作为黏接管，为无缝隙连续体，其复合层具有一定的微观特性，本文在进行数值分析求解时，根据上述特性，提出以下假设：

1) 玻纤增强柔性管由内层、增强层和外层等3部分构成，其中增强层由玻纤和基体构成，基体是玻纤的黏结剂，所用材料为HDPE（High-Density Polyethylene）；

2) 玻纤增强柔性管的各组成部分均质，没有裂纹和空隙；

3) 作为黏接型柔性管，玻纤增强柔性管的增强层玻纤与基质是黏接的，受力时无相对滑移，层与层之间也没有相对滑移；

4) 在变形过程中，玻纤增强柔性管横截面与中性轴一直保持垂直。

1.2 玻纤增强柔性管在外压载荷作用下的运动方程

图1为玻纤增强柔性管示意，其中：R为变形前截面平均半径；z为截面上任一点到截面中线的距离；ζ为变形后截面上任意点到弯曲中性面的距离。在截面变形过程中，任一点的位移用轴向位移u、环向位移v和径向位移w来表示。假定变形前垂直于截面中线的平面与中线垂面之间可产生一定夹角θ，截面上任意一点的思向应变[3]为

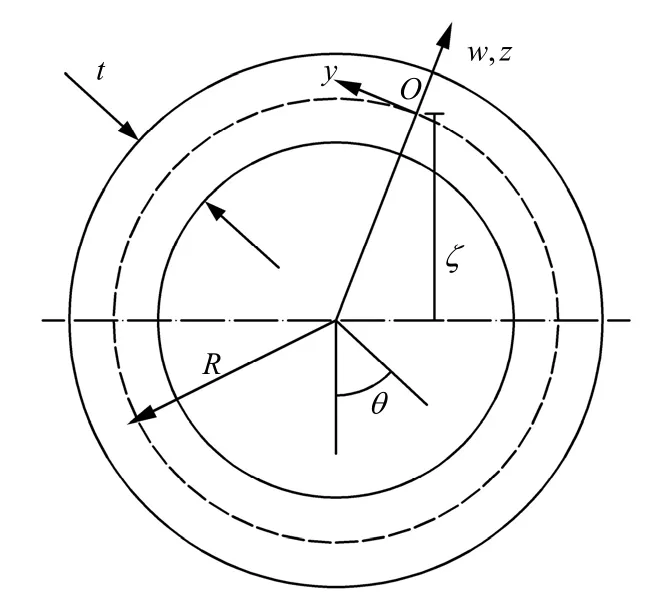
图1 玻纤增强柔性管示意

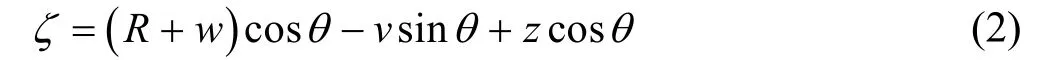
环向应变为

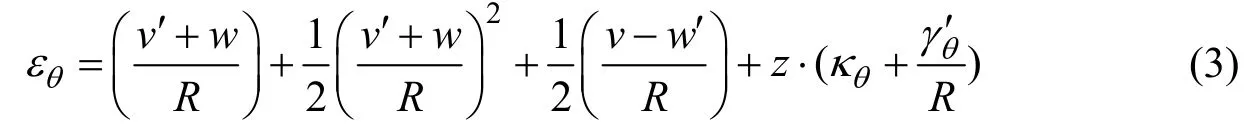
假设沿壁厚方向的剪应变为一阶线性，则有

式(5)中：θγ为沿壁厚方向的剪应变。

1.3 虚功方程

为得到外压载荷作用下玻纤增强柔性管的屈曲特性，基于非线性屈曲理论和虚功原理建立平衡方程及其附加方程，即

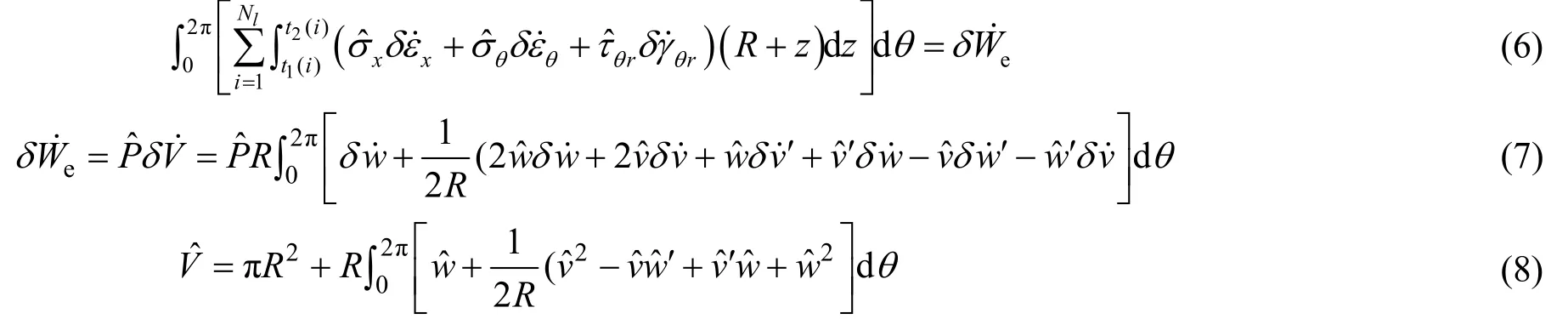
式(6)～式(8)中：xσ为轴向应力在上一个载荷步的值；上标∧表示变量的当前值；上标·表示载荷步间变量的增量；N1为总的分析步；t1(i)和t2(i)为截面上第i层在截面上沿厚度的坐标；xε为轴向应变；θσ为环向应力；θε为环向应变；rθτ为剪切应力；We为外压做的功；P为外压。联立式(6)～式(8)可得到各给定体积值下管道的外压值，以及相应状态下截面各点的应力、应变和位移。

1.4 数值分析流程

平衡方程中出现的积分计算采用数值积分的方法实现。数值积分采用高斯积分的方法实现，首先将管道的截面分别沿环向和径向划分为m个单元和n个单元，根据高斯积分点的取法在截面上分配高斯积分点。

根据虚功方程建立的方程组为非线性方程组，采用 Newton-Raphson法对该非线性方程组进行数值求解。即对于形如式(9)的非线性方程组，按式(10)所示的方法进行迭代，直到2次迭代值的差小于一个小值，即认为结果收敛。

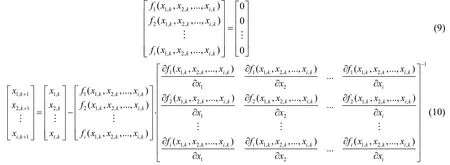
计算中对管道的加载是通过加很多载步完成的。在外压计算中：对外压的加载是通过指定单位长度管道的体积完成的，在每个荷载步中预先给定变形之后的体积值，通过迭代计算得到给定体积值下截面各点的位移值和相应的外压值；对弯曲的加载是通过指定曲率完成的，在每个荷载步中预先给定曲率值，通过迭代计算得到给定曲率下截面各点的位移值。根据每步的位移值又可计算出各点的应变增量，根据应变增量与增量形式的本构关系计算各点的应力增量，最终可求得每个荷载步下各点的外压、位移、应变和应力等参数的数值。整个过程在MATLAB中编程实现，数值分析流程图见图2。

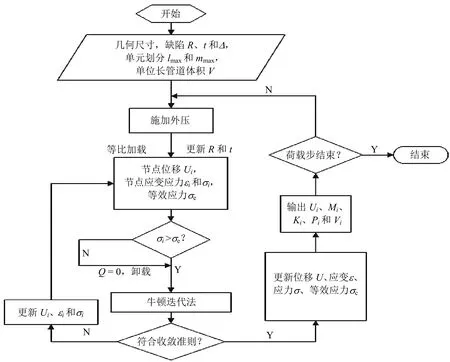
图2 数值分析流程图

2 有限元分析

下面根据玻纤增强柔性管的真实结构，利用有限元软件ABAQUS建立三维有限元模型，并进行模拟分析。在工程应用中，玻纤增强柔性管实际长度与管道外径的比值往往较大，因此可将玻纤增强柔性管作为无限长管进行研究。在有限元仿真中，可从建模可行性的角度考虑，取一小段管道进行研究。

2.1 几何参数和材料性能

玻纤增强柔性管模型的外径为76 mm，内径为50 mm。玻纤增强柔性管截面参数见表1和表2，有限元材料参数见表3。

表1 玻纤增强柔性管截面参数（内衬层和外保护层）

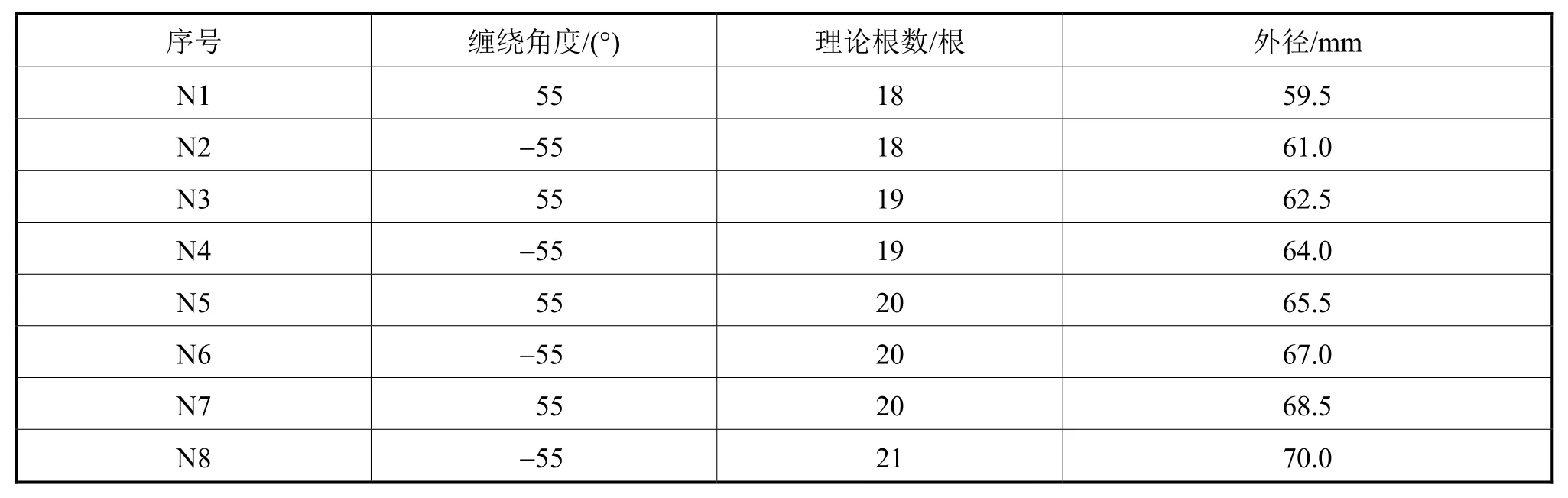
表2 玻纤增强柔性管截面参数（增强层）

表3 有限元材料参数

2.2 有限元模型建立

建立一个20 mm长的有限元模型。在建模过程中，采用Python语言，在ABAQUS的Kernel Command Line Interface界面导入脚本文件，方便在建模过程中对参数进行设定。假设各层之间相互紧密连接，先利用Extrusion命令建成模型，再利用Partition命令分割各层，并将材料属性赋予各层，将内外层和基体设置成固体单元，将玻纤设置成梁单元；在实际建模过程中，将基体与内外层设置成一个part，将各层的玻纤设置成单独的part，并对每层的玻纤进行阵列[5]。外压有限元分析分为2步，其中：第一步为模态分析，分析步选择 Perturbation-buckle类型，选取一个较小的因子，并将其与得到的模态位移相乘，将所得结果作为初始缺陷添加到管道上；第二步为静力分析，得到管道在外压下的屈曲特性。

边界条件设定：一端选取为z轴的固定约束（U3=UR1=UR2=0），另一端对沿U3方向（即长度方向）的自由度进行耦合约束，并在相应的耦合点上施加其余5个自由度方向的转角和位移控制条件。施加该约束条件是为了使参考点在管道截面的平面内不发生偏移和转动等，使截面各节点的运动在遵从参考点的运动时与实际情况更吻合。玻纤增强柔性管的边界条件见图3。

2.3 有限元计算结果

图4为采用数值分析方法和有限元分析方法得到的椭圆度-外压关系曲线对比。2条曲线的变化趋势相同，外压随椭圆度的增加先增大后减小，外压最大值为16.49 MPa，此时的椭圆度为4.60%。

图5～图7分别为玻纤增强柔性管在外压载荷下最终破坏时刻内层UHMWPE的应力云图、玻璃纤维的应力云图和外层HDPE的应力云图。

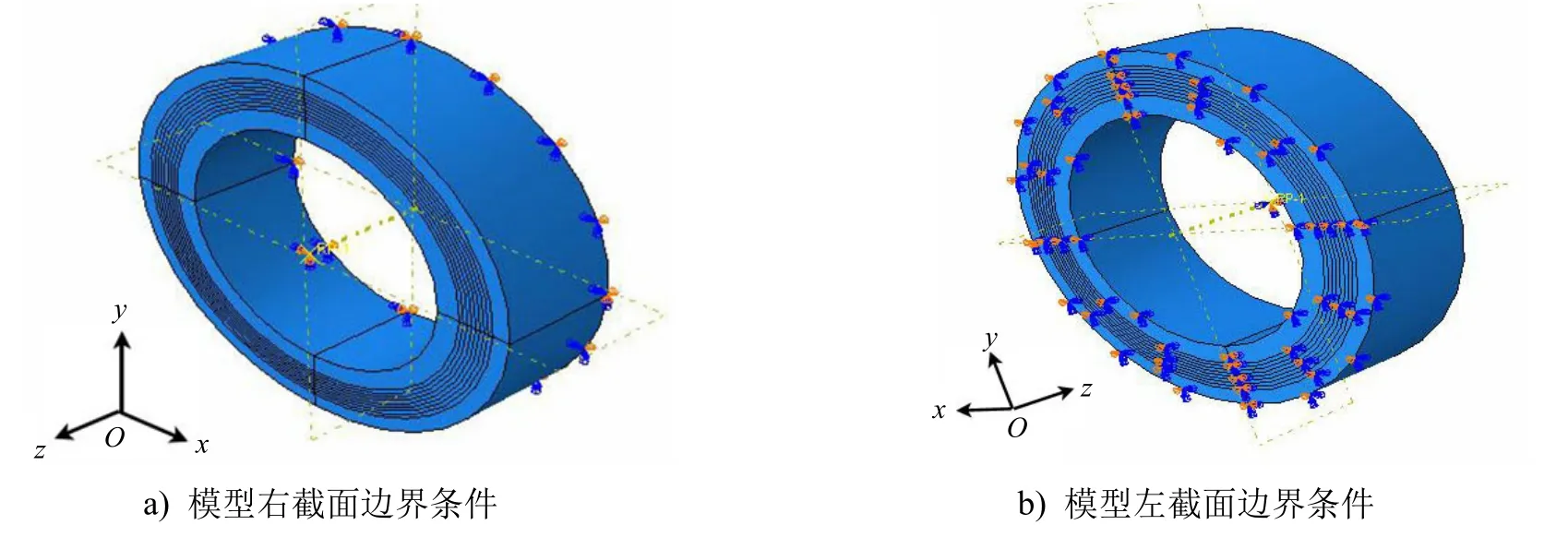
图3 模型边界条件

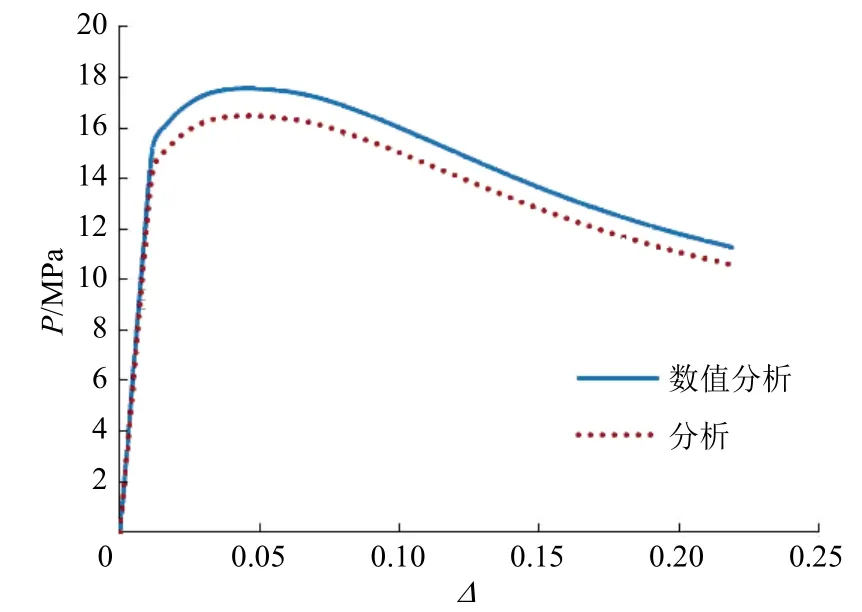
图4 采用数值分析方法和有限元分析方法得到的椭圆度-外压关系曲线对比

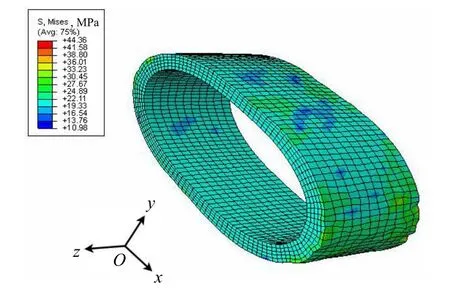
图5 外压载荷下内层UHMWPE的应力云图

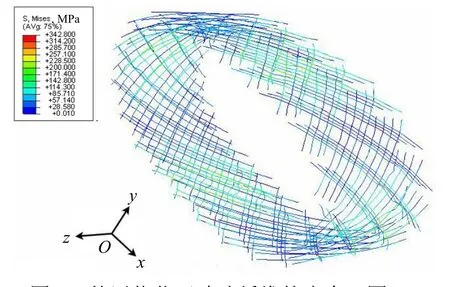
图6 外压载荷下玻璃纤维的应力云图

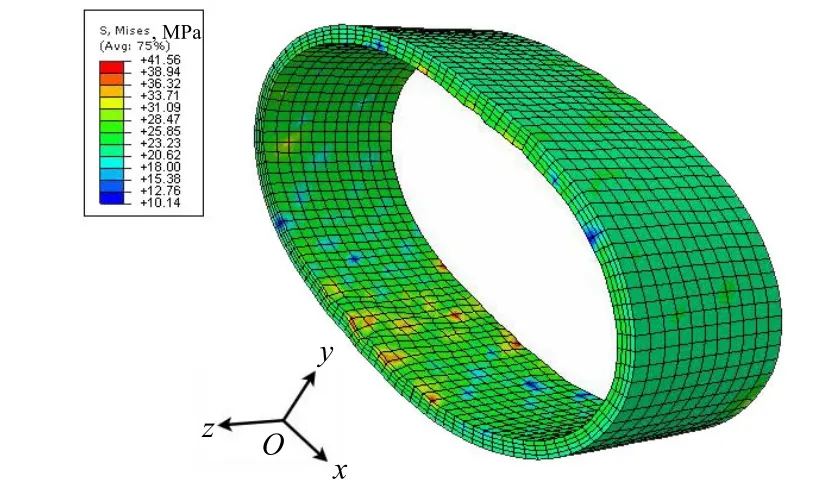
图7 外压载荷下外层HDPE的应力云图

通过对比可知：数值分析计算结果与有限元计算结果相近，最大外压承载力的误差小于 7%；数值分析采用与有限元不同的平截面假定导致二者产生相对误差。

3 外压试验

3.1 样管

外压试验样管（见图8）采用的是上海飞舟博源公司提供的玻纤增强柔性管，3根试验样管的基本几何参数见表4。根据规范ASTM D2412-02，样管的有效长度大于300 mm，符合试验要求。

图8 外压试验样管

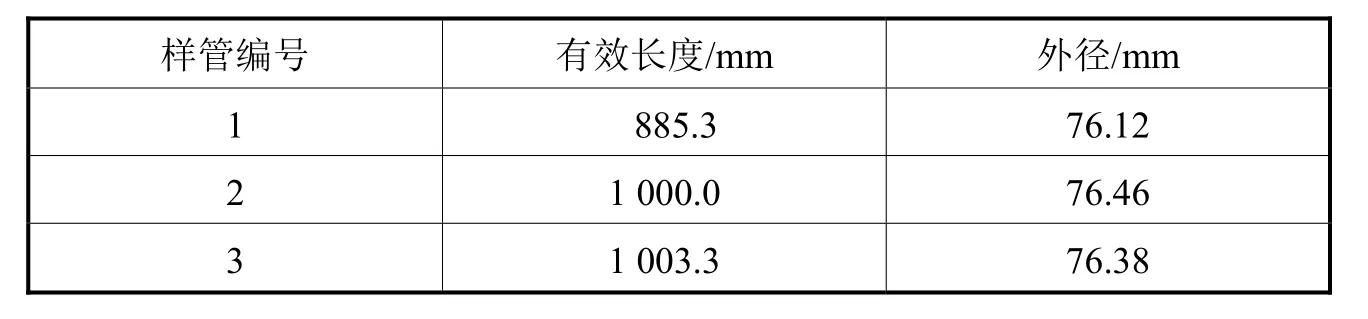
表4 试验样管的基本几何参数

3.2 试验结果

对外压承载力进行测量，将玻纤增强柔性管密封之后置入压力容器内，以水为介质施加压力，将压力突降和样管体积突变作为玻纤增强柔性管失效的标志。图 9为失效之后的玻纤增强柔性管样管，出现明显的屈曲现象。表5为样管失效时的屈曲值。

图9 失效之后的玻纤增强柔性管样管

表5 样管失效时的屈曲值

3.3 结果对比

通过短期外压载荷试验得到最大外压承载力的平均值为18.33MPa。采用数值分析方法得到的外压承载力为17.58 MPa，与试验结果的相对误差为4.09%。造成误差的主要原因为：

1) 数值分析忽略了端部效应，即接头处管道仍保持圆形并承受由静水外压产生的轴向压力；

2) 数值分析方法对玻纤增强柔性管的结构和外压载荷下的屈曲过程做了假设；

3) 实际生产的样管参数与详细设计的样管参数有差异。

4 结 语

本文研究了外载荷下玻纤增强柔性管的力学性能，采用数值分析、有限元模拟和试验等3种方法对玻纤增强柔性管进行了研究。通过对采用这3种方法得到的最大外压承载力进行对比，发现相对误差较小，符合实际工程的要求，说明采用数值分析方法计算玻纤增强柔性管的最大外压承载力是可行的。