基于渠系输水模拟与土壤水量平衡模拟的两级渠系优化配水模型

潘 琦 夏 爽 郭珊珊 单宝英 郭 萍*

(1.中国农业大学 水利与土木工程学院，北京 100083； 2.中国水利水电出版社有限公司，北京 100038)

2017年我国农业用水总量占全国总用水量的62.3%，农田灌溉水有效利用系数仅为0.548[1]，农业用水浪费现象严重。随着社会经济的发展和城市化进程的加快，各用水部门之间竞争激烈，农业灌溉用水供需矛盾日益突出，在我国水资源极度短缺的西北干旱区，农业用水形势尤为严峻。为保障农业的可持续发展，需要提高农业用水效率，加强农业灌溉管理。灌区是灌溉农业生产的重要载体[2]，我国大部分灌区都存在用水效率不高的问题，其中一个关键的原因就是灌区管理部门不能科学有效地对有限的水资源进行有效的分配和管理。实践表明，节水潜力的50%在管理上[3]。通过优化模型的构建，为灌区管理部门制定一套节水增产的优化配水方案至关重要。

国内外目前对渠系优化配水的理论研究已经取得了较多的成果。根据优化主体的不同可将渠系优化配水分为以下几类：第一类以农民和管理部门利益为主体，目标多为产量最大[4]、经济效益最大化、供水成本最小化[5]等；第二类以渠系运行情况为主体，目标多为渠道输水量或渗漏损失最小[6-8]、轮灌组最少[9]、水流相对平稳[10-11]等；第三类以“定流量、变历时”的理论为主体，目标多为渠道配水时间最短[12-13]、引水时间均一化[14]、轮灌组间引水持续时间差异最小[15]等。然而，这三类优化模型的建立都只考虑了优化对管理部门或渠系运行一方面的影响，忽略了农业灌溉的根本——作物本身对水的需求，而作物的需水量又难以找到一个绝对的量化标准，因此可以用土壤水量的变化来反映作物对水分的需求。基于此，本研究拟将渠系优化配水模型与土壤水量平衡模型耦合，构建基于渠系输水模拟和土壤水量平衡模拟的灌区两级渠系优化配水模型，同时提出求解该复杂优化模型的有效算法，制定满足渠系运行要求和土壤水量的灌水方案，以期模型贴近灌区实际情况，为今后管理部门的决策提供依据和指导。

1 渠系优化配水模型与算法

1.1 模型建立与预处理

本研究以种植作物产量最大和灌溉时的配水量最少为目标函数，决策变量为下级渠道净流量。通过土壤水量平衡模型得到作物生育期内土壤含水量的动态变化，通过土壤含水量的变化确定作物需水要求，引导优化模型制定灌水方案。本研究对水量、渠道流量和土壤含水量进行约束，使用改进的遗传算法求解该多目标模型的Pareto解集，并用罚函数法对不满足约束的结果进行处理。

目标函数：

1)引入Jensen模型描述作物需水量与产量的关系，即作物实际产量等于最大产量与实际作物需水量和潜在作物需水量比值的乘积，区域作物最大产量用各下级渠道的作物单产乘以控制面积表示。因此，实现种植作物产量最大目标的函数表示为：

(1)

式中：Ya,sum为渠系控制面积上的作物总产量，kg；k为下级渠道编号，共有K条下级渠道；Sk为下级渠道的控制面积，hm2；Ym,k为下级渠道控制面积上的作物在充分灌溉条件下的单产，kg/hm2；n为作物各生育期的编号，共有N个生育期；ETa,n为作物在各生育期的实际作物需水量，mm；ETm,n为作物在各生育期的潜在作物需水量，mm；λn为作物在各生育期对水分亏缺的敏感指数。

2)灌溉过程中，水流经渠系时会有一定的渗漏损失，这部分水量在渠系配水时也应当考虑，因此，实现配水量最少目标的函数为：

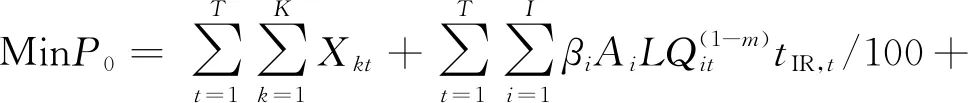
(2)

式中：P0为上级渠道的配水量，m3；Xkt为第t天下级渠道灌入田间的水量，m3；i为上级渠道编号，共有I条上级渠道；t为自作物生育期第一天起到最后一天的天数序号，T为作物生育期总天数；Qit为第t天上级渠道的配水净流量，m3/s；qkt为第t天下级渠道的配水净流量，m3/s；tIR,t为上、下级渠道在第t天的灌水时间，s，取为24 h(即86 400s)；βi、βk分别为上、下级渠道采取防渗措施后渗漏水量的折减系数；Ai、Ak分别为上、下级渠道的渠床土壤透水系数；m为上、下级渠道的渠床土壤透水指数。

第t天下级渠道灌入田间的水量与上级渠道的配水净流量表示为：

Xkt=qkt·tIR,t

(3)

(4)

约束条件主要有水量约束、渠道流量约束、土壤含水量约束和节点流量约束，表示如下：

1)水量约束如式(5)和(6)：

P0≤W

(5)

(6)

式中：W为上级渠道可提供的水量，m3；Mn为作物各生育期的最小需水量，m3。

该约束的罚函数为：

(7)

(8)

2)渠道流量约束为式(9)和(10)：

(9)

(10)

式中：Qu、qd分别为上、下级渠道的设计流量，m3/s；Jd、αd分别为上、下级渠道的最小流量折减系数；Ju、αu分别为上、下级渠道的加大流量系数。

该约束的罚函数为：

(11)

(12)

3)土壤含水量约束：

60%θmax≤θkt≤θmax

(13)

式中：θmax为下级渠道的控制面积上的田间持水量，mm；θkt为下级渠道控制面积上的土壤含水量，mm。土壤含水量的下限值取为田间持水量的60%。

该约束的罚函数为：

(14)

4)节点流量守恒约束：

(15)

式中：Qa、Qb分别为节点a、b处的流量，m3/s；ΔQ为渠道的输水损失流量，m3/s。渠道最小流量折减系数与加大流量系数采用经验系数[16]。流量节点位置示意见图1。

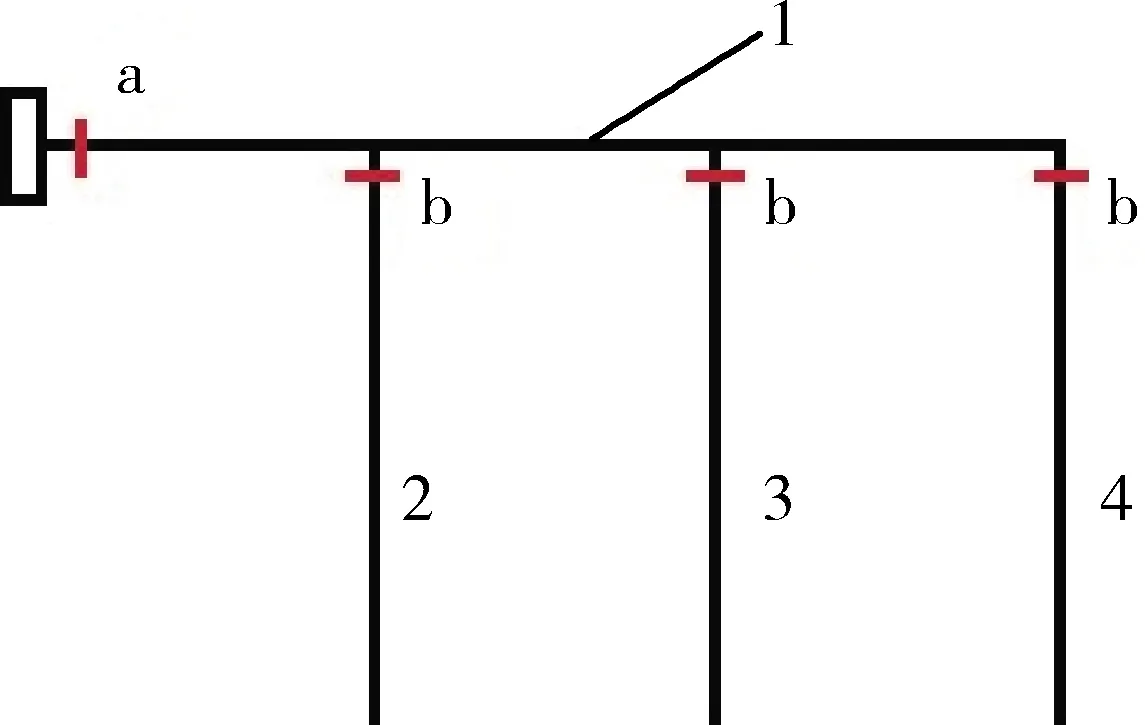
1为上级渠道，2、3、4为下级渠道；a为上级渠道流量守恒节点，b为每条下级渠道的守恒节点。 1 is the superior canal. 2, 3 and 4 are the lower canals. a is flow conservation node for superior canal. b is flow conservation node for each lower canal.
图1 两级渠道流量节点位置示意图
Fig.1 Location diagram of two-level canal flow nodes

1.2 土壤水量平衡模型

土壤水量平衡可以有效地表征土壤水分变化对作物耗水的影响以及作物对水量的需求，本研究通过Kanooni等[12]提出的土壤水量平衡公式来反映日尺度上土壤水量的变化情况，后一天的土壤水含量是由前一天的土壤水含量、灌水量、降水量、作物耗水量、深层渗漏量以及作物根系生长量共同确定的，土壤水量平衡公式表示为：

θkt+1=θkt+IRkt+Pkt-ETa,kt- DPkt+θ0(Rkt+1-Rkt)

(16)

式中：θkt+1为下级渠道控制面积后一天的土壤水含量，mm；IRkt为下级渠道在第t天灌入田间的灌水深度，mm；Pkt为下级渠道在第t天的降水量，mm；ETa,kt为下级渠道控制面积上的作物在第t天的实际作物耗水量，mm；DPkt为下级渠道控制面积在第t天的深层渗漏量，mm；θ0为初始土壤含水量，取田间持水量0.196[17]，mm/m；Rkt+1、Rkt为下级渠道控制面积上前后两天的作物根系长度，m。

1)灌水深度。下级渠道每天灌入田间的水量用灌水深度表示，即：

(17)

式中：ηf为灌溉水利用系数，参考甘肃省张掖市样点灌区2016年农田水灌溉水有效利用系数测算分析结果报告取为0.576；B为闸门启闭1次造成的损失，m3，取为1 500 m3[18]。

2)实际作物耗水量。式(16)中实际作物耗水量通过参照作物需水量ET0、作物系数Kc和水分胁迫系数Ks相乘求得：

ETa,kt=ET0·Kc·Ks

(18)

其中，作物系数Kc由陈军武等[19]得到的制种玉米各生育阶段作物系数结合张芮[20]试验得出的制种玉米耗水规律调整得到，其在各生育阶段的数值分别取为0.50、0.70、1.19、0.60；水分胁迫系数Ks参考裴源生等[21]公式，如式(19)。根据生育期第一天的土壤含水量推求Ks，再计算得到ETa,kt值，从而得到第二天的土壤含水量，由此推求第二天的Ks，以此类推。

(19)

式中：θ为土壤含水量与田间持水量的比值，%；θc为土壤水分胁迫临界含水量与田间持水量的比值，%，本研究中取为60%；ε为经验系数，本研究中取为0.89。

3)作物根系长度。参考Kanooni等[12]对土壤水量平衡公式中各分项的计算方法，使用一种适用于一般作物的作物根区生长计算公式[22]：

(20)

式中：Rt为第t天的作物根系长度，m；r为播种深度，m；Rmax为根系最大生长长度，m。

夏爽[18]将式(20)应用于黑河中游制种玉米根长的计算中，并对其进行修正，首先将作物根系生长期分为生长初期、发育期和生长中期、生长后期3个阶段，并确定生长初期和生长后期的根长分别为定值0.3 m和0.8 m，因此式(20)只用于计算作物发育期和生长中期的根长。将式(20)与修正后的式(21)进行对比，发现修正公式计算结果与原式计算结果差距较小，不会影响计算的准确性且一定程度上提高了模型的求解速度，因此选用式(21)计算作物发育期和生长中期的根系长度。

(21)

1.3 算法概述

本研究是一个多目标优化问题，根据实际情况或不同决策者的偏好，问题的最优解可能有很多，因此采用Pareto解集可以更好的满足决策需求。对于求解多目标优化问题的Pareto最优解，常用的有权重系数变换法、并列选择法和排列选择法[23]。本研究选取权重系数变换法，它是为每个目标函数赋予不同的权重，再将各个目标函数加权求和，以此来得到问题的最优解，当对每个目标函数赋予不同的权重时，就会得到不同权重下的最优解，将这些最优解组成的解集表示在同一坐标系上，就会产生一个Pareto前沿面。这种方法将复杂的多目标优化问题转换为单目标优化问题，简便了算法，具体求解步骤如下：

1)编码。本研究中，对决策变量产生的个体使用长度相同的十进制符号串表达，决策变量为各个渠道在生育期中每天的配水净流量。

2)产生初始种群Ns。初始种群是一个采用均匀分布的0～1之间随机数的方法产生的二维矩阵。结合农业灌溉实际，灌水时间相比作物生育期总时间少得多，因此，人为编写程序语言使个体的qkt基因为数值0的增多。模型的约束较多可能会导致算法搜索时找不到可行解，为加快收敛速度，预先生成多于初始种群数目的种群，并且在进入遗传算法前先找到可行解，再进入遗传算法，筛选出符合条件的初始种群。

3)适应度值的评估。本研究使用权重系数变换法求解目标函数，并使用罚函数法对不满足约束的结果进行处理。若适应度值小，则在种群中的排序靠前，遗传到下一代中的可行性就大；若适应度值大，则在种群中的排序靠后，在遗传过程中被淘汰。为使各惩罚项的数值与目标函数值处于同一数量级，需要给各惩罚项赋予一定的权重。适应度函数表示为：

MinZ=Cy(Ym-Ya,sum)+C0P0+C1P1+C2P2+C3P3+C4P4

(22)

式中：Cy、C0为目标函数的权重值；C1、C2，…，C4为各惩罚的权重系数；Ym为由潜在产量得到的渠系控制面积上的最大产量，kg。

4)选择、交叉和变异。变异采用动态确定变异概率的策略，这样可以防止优良基因遭受变异而受到破坏，也可以在陷入局部最优解时提供新的基因，提高收敛速度。将个体按照适应度值排序，将种群个体分为4个部分，每个部分按照适应度值排序分别有机会产生4、3、2、1个子代，子代的变异概率由父代的适应度值排序动态确定。变异概率分为2种动态情境：当某一代的最优适应度值小于临界值时，产生的变异概率较小，从优向劣的个体变异概率从小变大，最优个体的子代变异概率为0.001，最劣个体的子代变异概率从0.1开始随迭代次数的增加而减小至0.002；当某一代的最优适应度值大于临界值时，最优个体的子代变异概率为0.01，最劣个体的子代变异概率为0.5。再将生成的子代与上一代个体混合，进行适应度值评价，筛选出前Ns个个体作为变异后的新种群。

选择使用排名的策略。将个体按照适应度值排序，将种群个体分为4个部分，每个部分按照适应度值排序分别有机会产生4、3、2、1个子代，每次随机选择5个配偶，选取其中性能最好的作为母本进行交叉。

交叉采用择优随机交叉的策略，每个个体都至少交叉1次。每次交叉都会随机生成一个与个体大小相同的0-1矩阵，其中元素0表示子代矩阵中对应位置的基因继承父本，元素1则表示子代矩阵中对应位置的基因继承母本。择优随机交叉后，Ns个父本产生3倍的子代，将子代与父代混合后再次进行适应度值评价，最终筛选出前Ns个个体作为新种群。

5)控制参数的确定。种群为目标函数中的决策变量qkt，为使算法的结果更加稳定可靠，设置初始种群Ns数目为500，种群规模为下级渠道数量J，迭代次数为100次，目标函数的权重值组数为50组。

2 实例应用

2.1 研究区域概况

本研究选取位于甘肃省河西走廊中部、黑河中游西岸、张掖市甘州区西南37 km处的西干灌区沿河总干渠下辖的沿河分支渠及其下级渠道进行实例验证。西干灌区是以引黑河水自流灌溉为主、井灌为辅的大型灌区。灌区控制面积3.33 万hm2，地势较为平坦，总体上由东南向西北方向倾斜。灌区海拔1 400～1 500 m，属大陆性温带干旱气候，年均气温7 ℃，最低气温-29.1 ℃，最高气温38.6 ℃，多年平均降水量为123 mm，多年平均蒸发量为2 047.9 mm，最大冻土深度125 cm，年无霜期145 d，年日照时数3 067 h。该处具有日照时间长、昼夜温差大、降雨稀少且时空分布不均、蒸发量大等特点。灌区现有干渠、分干渠11条共计91.9 km，支渠、分支渠46条共计183.62 km，斗渠206条共计371.72 km，设计灌溉面积2.46 万hm2，有效灌溉面积2 万hm2。张掖市是全国的玉米种子培育基地，灌区制种玉米的种植面积达到1.73 万hm2以上，此外灌区还种植小麦、大豆、蔬菜、油料等粮食经济作物。根据西干灌区2016年各渠系灌溉面积及引水量统计表可知，沿河分支渠的控制面积内只种植制种玉米，来水量为823.58 万m3。西干灌区沿河分支渠渠系基本信息见表1，沿河分支渠下辖5条斗渠，但由于沿河五斗与其他4条斗渠的控制面积差距较大，可忽略不计。简化后的西干灌区沿河分支渠渠系分布情况见图2。

表1 西干灌区沿河分支渠渠系基本信息Table 1 Basic information of Yanhe branched canal in Xigan irrigation district

编号1，2，3，4分别表示沿河一斗、沿河二斗、沿河三斗、沿河四斗。 Numbers 1, 2, 3 and 4 represent the 1st， 2nd， 3rdand 4thlateral canals.
图2 西干灌区沿河分支渠渠系分布情况
Fig.2 Distribution of Yanhe branched canals in Xigan irrigation district

2.2 模型参数

制种玉米生育期划分和水分亏缺敏感指数借鉴张芮[20]的试验，4月20日—6月7日为播种—拔节期、6月 8日—7月12日为拔节—抽穗期、7月13日—8月9日为抽穗—灌浆期、8月10日—9月24日为灌浆—成熟期，各生育期的水分亏缺敏感指数依次为0.05、0.70、0.19、-0.03。西干灌区沿河分支渠及其下属斗渠相关参数见表2[16]。

选取张掖地区2016年4—9月的气象数据得出该地区参照作物需水量在4—9月的日均值，依次为1.825、2.700、4.124、4.663、4.123、4.639 mm/d。

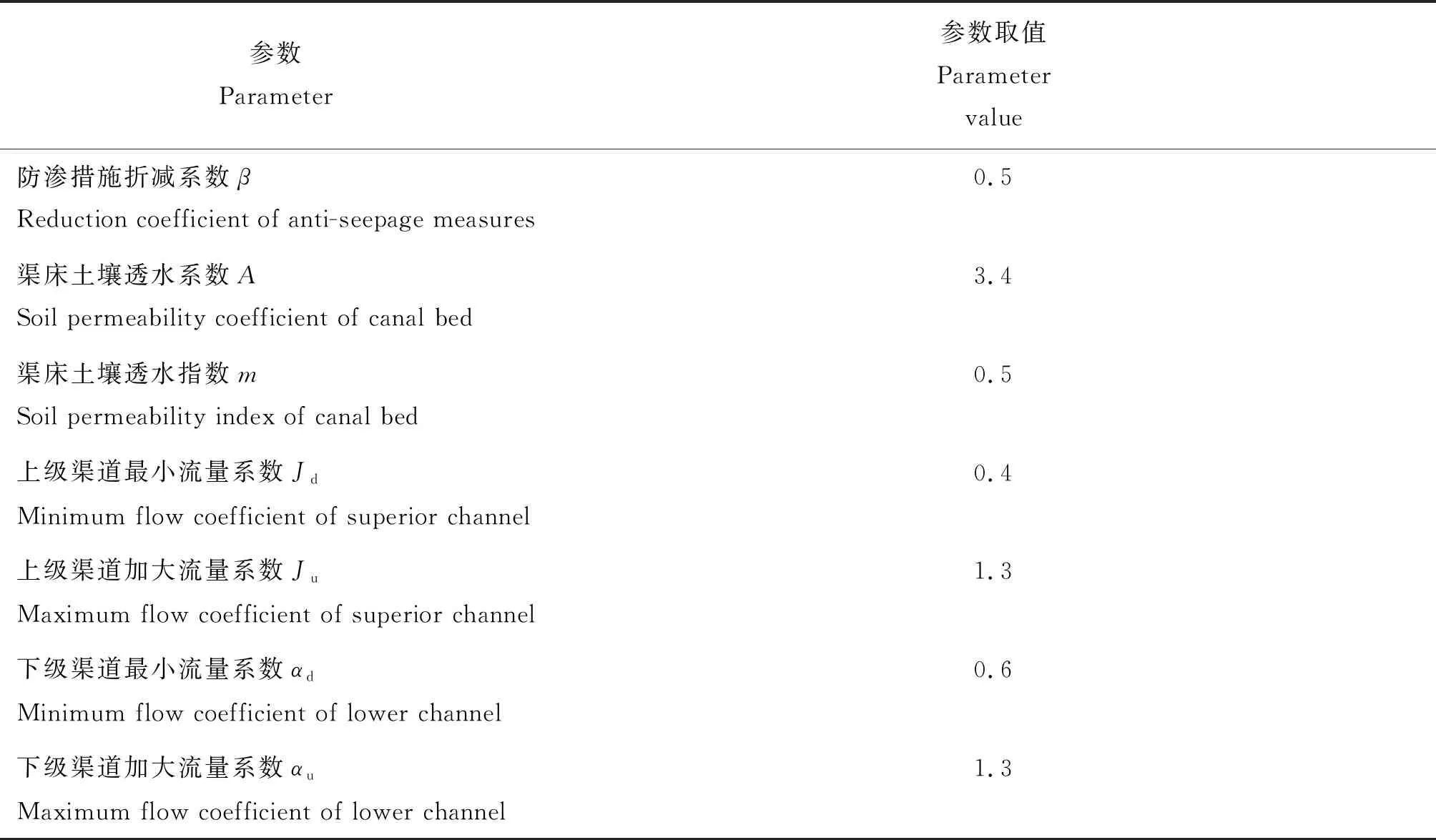
表2 西干灌区沿河分支渠及其下属斗渠相关参数Table 2 Parameters of Yanhe branched canal and lateral canals in Xigan irrigation district

2.3 结果与分析

使用MATLAB编写多目标改进遗传算法的程序求解该渠系优化配水模型，共求得50组非劣的渠系优化配水方案。

2.3.1Pareto解集

求解模型得到的Pareto前沿面较稳定，说明模型及改进遗传算法的稳定性较好，没有与预期结果产生较大的偏离，进入遗传算法后也没有陷入局部最优解。得到的Pareto前沿面省去了事先确定各个目标的权重值这一步骤，避免了权重值选取不当而错过优选方案的问题，还可以生动地体现目标之间的博弈关系，在灌区管理部门做决策时提供更多信息[24-25]。本研究选取3组代表性方案进行对比分析，将选取的配水量最少目标权重为0.995、产量最大目标权重为0.005的方案命名为1号方案，配水量最少目标权重为0.515、产量最大目标权重为0.485的方案命名为2号方案，配水量最少目标权重为0.049、产量最大目标权重为0.951的方案命名为3号方案。1～3号方案分别代表上级渠道配水量最少、2个目标均处于中间水平和总产量最大时的最优解。求解模型得到的Pareto前沿面见图3。

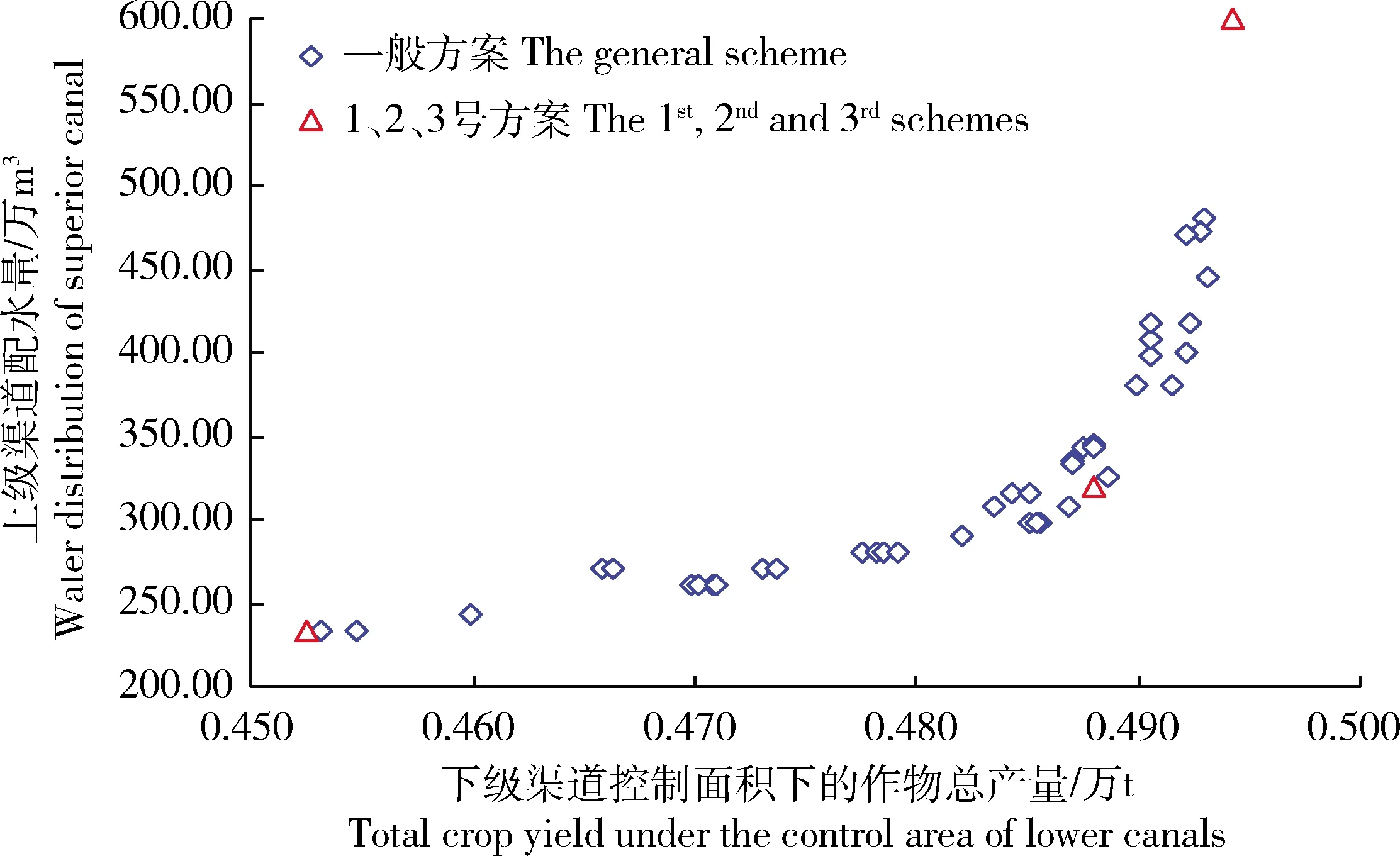
图3 求解模型得到的Pareto前沿面
Fig.3 Pareto frontier by solve the model

2.3.2产量和配水量结果分析

1～3号方案求解得到下级渠道控制面积下的作物总产量依次为0.452、0.488和0.494 万t；上级渠道配水量依次为234.79、320.51和599.06 万m3，均远小于西干灌区沿河分支渠的可供水量。从结果来看，产量与配水量之间存在较强的相关性，即在约束范围内，配水量越多，得到的作物产量越多，这是符合实际生产情况的。从1号方案到2号方案，多配水85.72 万m3，就可以多获得360 t的制种玉米，然而从2号方案到3号方案，需多配278.55 万m3的水才可以获得60 t的制种玉米，说明3号方案虽然可以通过增加配水量来增加产量，但是产量增加并不明显，同时对水资源造成了较大的浪费。1～3号方案得到的各下级渠道控制面积下的作物单产见图4。1号方案4条下级渠道的单产差距较大，且各条渠道的单产与其他2个方案相比有较大差距，这是因为1号方案过于追求配水量最小，而忽略了农业种植最关键的收益问题。因此，灌区管理者在进行决策时，应根据预期得到的产量对配水进行控制。考虑到西干灌区是制种玉米的种植基地，需要保证一定的产量，又地处干旱区、水资源极度匮乏，建议管理者在决策时考虑2号方案附近的决策结果。

2.3.3土壤含水量分析

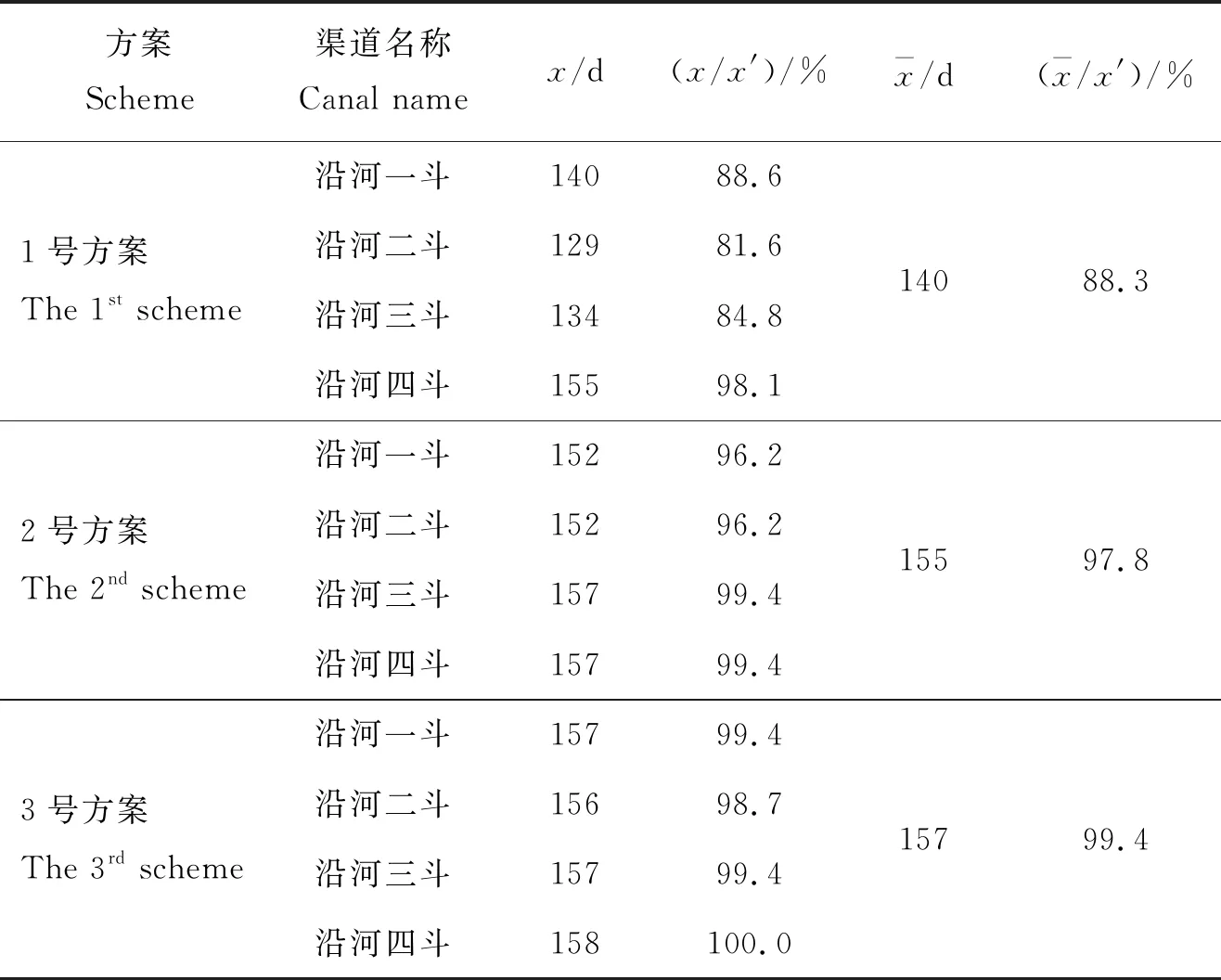
下级渠道满足土壤含水量约束的时间及其占全生育期比例见表3。1～3号方案中各下级渠道平均满足土壤含水量约束的时间分别是140、155和157 d，占全生育期的比例依次为88.3%、97.8%和99.4%。2号方案和3号方案下土壤含水量约束的满足情况很好，说明在这2种方案下灌入田间的水量充足，能够保证作物生长所需的水分，且不会因水分亏缺影响作物与水分相关的指标；1号方案下土壤含水量约束的满足情况一般，且土壤缺水大多发生在制种玉米的拔节期和灌浆期，很容易影响作物的生长发育。通过对土壤含水量的分析，得知1号方案虽然把配水量降到很小，但是已经影响到了作物正常的生长发育，这有可能导致作物产量过低，这与2.3.2的结果是相符的；同时，2号方案和3号方案下配水量可以满足土壤含水量的需求，但如前述3号方案会造成水资源的浪费，因此建议灌区管理者优先按照2号方案进行配水。

图4 1～3号方案各下级渠道控制面积下的作物单产
Fig.4 Crop yield of per unit under the control area for lateral canals under the 1-3 schemes

表3 下级渠道满足土壤含水量约束的时间及其占生育期比例
Table 3 Time satisfying the soil moisture content and its proportion in growing period at lateral canals

方案Scheme渠道名称Canal namex/d (x/x')/%x/d(x/x')/%1号方案The 1st scheme沿河一斗14088.6沿河二斗12981.6沿河三斗13484.8沿河四斗15598.114088.32号方案The 2nd scheme沿河一斗15296.2沿河二斗15296.2沿河三斗15799.4沿河四斗15799.415597.83号方案The 3rd scheme沿河一斗15799.4沿河二斗15698.7沿河三斗15799.4沿河四斗158100.015799.4

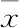
2.3.4作物耗水量分析

1～3号方案下各下级渠道作物的实际耗水量见表4。将各生育阶段的实际作物耗水量与潜在作物需水量对比发现，播种—灌浆期实际作物耗水量的趋势基本与潜在作物需水量一致，但是在灌浆—成熟期实际作物耗水量的数值普遍偏小，分析有以下2种原因：一是利用气象数据计算参照作物需水量时只选取了1年的数据，数据量过小不具有代表性；二是作物系数的选取参考他人试验结果得到，不具有本研究区域的典型性。1号方案的平均实际作物耗水量偏小，结合前面的分析，可以认为1号方案的优化配水效果较差，管理者在决策时可以直接舍弃类似方案。同时，2号方案和3号方案在平均实际作物耗水量上的数值差距较小，为达到节水增产的双目标，推荐选取2号方案作为优化配水的最佳方案。

表4 不同方案下各下级渠道作物的实际耗水量Table 4 ETa of the lateral canals in different schemes mm

2.3.5最佳方案与灌区实际配水方案对比

根据甘肃省张掖市甘州区西干管理所的灌溉资料，西干灌区制种玉米各生育阶段的实际净灌水量见表5。选用2号方案与实际灌水方案作对比可知，模型得到的最佳方案的灌水主要集中在拔节—灌浆期，而实际灌水方案则较为平均，且2种方案在灌浆—成熟期有显著差别，原因是2号方案在前几个生育期灌水充足，土壤含水量较高，为了避免水资源的浪费，尽量减少了最后一个生育阶段的配水，使其充分利用土壤水。同时根据表4中的作物潜在需水量可知，灌浆-成熟期的需水小于前一个阶段，因此实际灌水方案很可能会造成水资源的浪费。参考夏爽[18]根据灌区作物灌溉制度手动设计配水方案的方法，得到西干灌区沿河分支渠及其下级渠道的实际灌水方案并代入模型计算，表6展示了2种方案得到的各渠道的灌水次数和单产，可以明显看出最佳方案的灌水次数比设计灌水方案多，各条渠道作物的单产也较大，结合表5的总灌水量可知，优化后的灌水方案达到了节水增产的目的。尽管如此，灌水次数的增加会增加管理人员和农民的工作负担，但对于西干灌区等水资源稀缺的西北内陆旱区，该研究仍然存在现实意义。实际灌水方案得到的上级渠道配水量为434.05 万m3，总产量4 220 t。最佳方案相比实际灌水方案在配水量上减少113.54 万m3，总产量却增加了660 t，说明优化后选取的最佳方案明显优于灌区实际灌水方案。

表5 最佳方案与实际灌水方案得到的各生育阶段的净灌水量

Table 5 The net irrigation water at each growth stage through the best scheme and actual irrigation scheme 万m3

方案Scheme生育阶段 Growing stage播种—拔节Sowing-Jointing拔节—抽穗Jointing-Heading抽穗—灌浆Heading-Pustulation灌浆—成熟Pustulation-Mature全生育期Total growingperiod最佳方案The best scheme76.27130.7786.276.07299.38实际灌水方案Actual irrigation scheme73.66103.4269.5569.55316.18

注：最佳方案即2.3.4中选取的2号方案。

Notes: The best scheme is the 2ndscheme selected in 2.3.4.

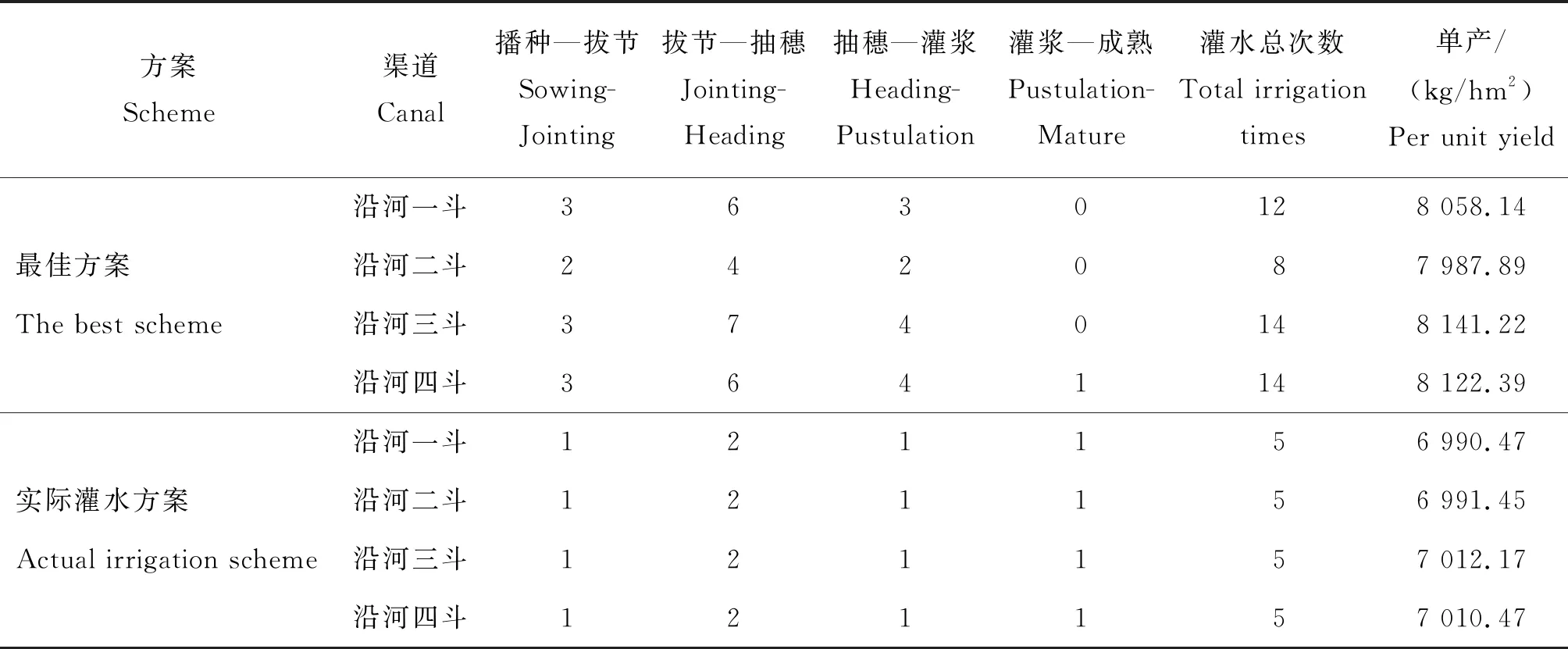
表6 最佳方案与实际灌水方案得到的各下级渠道灌水次数和单产Table 6 The irrigation times and per unit yield of each lateral canal through the best scheme and actual irrigation scheme

3 结束语

本研究建立了基于渠系输水模拟和土壤水量平衡模拟的渠系优化配水模型，采用求解多目标优化的改进的遗传算法进行求解。该模型考虑了渠系输水时产生的渗漏损失和作物生长发育必需的水量，通过模型的构建和求解得到了可以同时满足渠系运行要求和作物生长发育耗水量的优化配水方案。模型将下级渠道的配水净流量作为决策变量，以种植作物产量最大和灌溉配水量最少为目标函数，结合水量约束、渠道流量约束、土壤含水量约束和节点流量守恒约束，采用动态确定变异概率、子代与父代混合评估适应度等改进方法对传统遗传算法进行改进，并通过权重系数变换法改变目标函数的权重值从而得到Pareto前沿面。针对Pareto前沿面上的3个代表值进行对比分析发现，当2个目标函数的权重值处于中间水平时(2号方案)，无论是在产量目标还是配水量目标上都可以得到较好的满足，若权重偏向产量目标，则会造成不必要的水资源浪费，若权重偏向配水量目标，则会对产量乃至收益造成极大的影响。2号方案的结果显示，在上级渠道配水量为320.51 万m3时，作物总产量可达到4 880 t，土壤含水量与作物耗水量的满足情况都较好。同时，2号方案比实际配水方案在配水量上减少了113.54 万m3，总产量上增加了660 t，说明在该方案下优化模型可以达到节水增产的效果，能够帮助灌区管理者实行决策、为实际优化配水问题提供理论依据和科学指导。尽管如此，本研究只针对制种玉米一种作物，在今后的研究中，将会继续对模型和算法进行改进，使之适用于复杂渠系和不同种植结构。