圆形差分麦克风阵列的二阶波束形成器设计

郑毅豪， 巩朋成,2， 杜帮华， 张正文

(1 湖北工业大学电气与电子工程学院， 湖北 武汉 430068; 2 电子科技大学信息与通信工程学院, 四川 成都 611731)

麦克风阵列波束形成源于雷达阵列波束形成的思想，是多通道语音增强研究中的重要方法，在人机语音交互系统、助听器、车载免提语音通信、远程电视会议系统及机器人听觉等领域具有广泛应用[1]。波束形成器是一种空间滤波器，其主要功能是对特定方向的有用信号形成波束，同时抑制其他方向的干扰信号和噪声[2]。

传统的波束形成技术包括延迟—求和波束形成((Delay and Sum Beamforming, DSB)，最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成，广义旁瓣抵消(Generalized Sidelobe Canceller, GSC)算法等[3]。DSB算法首先对信号到达各个麦克风间的时间延迟进行估计[3-4]，然后对不同通道信号进行时延补偿，使得各通道在目标语音方向上达到同步，最后对各通道进行加权平均得到系统的输出。MVDR算法在保证目标方向语音信号不变的前提下，使得阵列的输出总功率达到最小。文献[5]提出了用于噪声环境中自动语音识别的鲁棒性MVDR波束形成算法，利用基于混合高斯模型的语音幅度谱求得的方向向量进而构建MVDR波束形成器。GSC算法由固定波束形成器、阻塞矩阵和自适应噪声消除模块三大部分组成：固定波束形成器用于带噪声的语音信号的初步增强；阻塞矩阵用来产生噪声参考信号；自适应噪声消除器利用阻塞矩阵产生的参考噪声信号来消除波束形成器输出信号中的残留噪声[6-7]。文献[8]提出了基于传递函数的广义旁瓣抵消算法(TF-GSC)，该算法通过估计声学传递函数的相对比值来构建波束形成器和阻塞矩阵，在方向性噪声场景下可以取得不错的效果，但在非方向性噪声如扩散噪声场下算法性能会下降。在麦克风阵列中实现上述算法功能需要较多的阵元，但在一些诸如手机、助听器之类的小型设备中不能使用大量的麦克风。

差分阵列(Differential Microphone Arrays，DMA)是利用相邻阵元的声压差实现波束形成，因此并不需要大量的阵元，且DMA具有频率不变特性、在相同的阵元数下可以获得最大的指向性和方向性，灵活多变的特点受到了广泛的关注。1995年G. W. Elko与A. T. N. Pong提出了一阶差分麦克分阵列技术(First-order Differential Microphone Arrays)，利用两个小间距麦克风在噪声方向形成波束零点[9]。传统的差分阵列设计方法虽然简便，但是针对不同波束模式的构建缺乏灵活性。对此，Benesty等人提出了在短时傅里叶变换域设计差分阵列的新方法[11]。2002年Luo等人在一阶差分阵列的基础上，提出了自适应零限(Adaptive Null-Forming)波束形成技术[12]，使得系统输出的波束零点自适应对准噪声方向。DMA常常因为空间白噪声而引起信噪比(SNR)异常，在DMA中把这种现象叫做白噪增益(WNG)，用它反映DMA处理噪声的能力，通过改变WNG的值，进而改善系统的稳定性。

传统的差分麦克风阵列是由多级级联方式实现的，每一级是通过取相邻阵元采集信号的时间差异性而得到相应的波束，这样设计的差分麦克风阵列结构复杂，而导致阵列的鲁棒性降低[10]。文献[13]提出了一种线性DMA的设计方法，将麦克风阵列信号转换为短时傅里叶变换(STFT)域，然后将DMA波束形成设计转化为简单的线性系统求解，该方法有较灵活的获得指定方向上的方向图，但是发现DMA的低阶输出模式在低频信号时有WNG的异常问题。文献[14]设计一种基于均方误差(MSN)准则的非对称的n阶DMA模型，该方法可降低白噪声对阵列波束图的影响。文献[15]提出了一种平面约束的鲁棒超定向波束形成器，将整个波束形成器分成两个子波束形成器，并将两个子波束形成器进行卷积设计出一种较低的指向性的波束图。

本文提出一种基于圆形差分阵列的二阶段波束形成器的设计，以解决DMA在二阶输出后白噪异常问题。该方案的特点是第一阶段与传统的差分麦克风阵列一阶响应相同，第二阶段通过引入白噪系数，获得最大的WNG方法构造的波束形成器，该方法不仅能够保持传统差分阵列频率不变的特性，而且解决了低频信号WNG异常导致阵列性能降低的问题，同时提高了差分麦克风阵列的阵增益。

1 模型建立与性能指标

本文考虑远场条件下的均匀圆形麦克风阵列模型。假设均匀圆形麦克风阵列的中心位于坐标系统的中心处，第1个阵元位于x轴上(图1)。

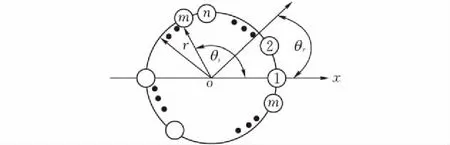
图 1 远场均匀圆形麦克风阵列模型

根据图1，假设远场信号到阵列的方位角为θr，则在远场条件下，信号到达第m个阵元与阵列中心之间的时间差为

Ym(ω)=Xm(ω)+Vm(ω)=

ejωcos(θr-θm)X(ω)+Vm(ω),

m=1,…,M

(1)

根据式(1)，M个麦克风阵列采集到的信号表示成向量形式为：

y(ω)=[Y1(ω),Y2(ω),…,YM(ω)]T=

d(ω,cosθr)X(ω)+V(ω)

其中，(·)T表示转置，d(ω,cosθ)表示信号到达阵列的方向导向矢量，在远场条件下，其值为：

(2)

本文考虑在麦克风阵列中通过设计滤波器系数h(ω)以提高信噪比(SNR)，达到降低噪声的目的。假设M个阵列接收到的信号经过滤波器为：

h(ω)=[H1(ω),H2(ω),…,HM(ω)]T

(3)

其中，Hm(ω)为第m个阵元的滤波器系数。因此，在期望方向θ处的波束方向图可表示为：

(4)

本文考虑利用阵列的输入信噪比(iSNR)和输出信噪比(oSNR)的比值表示SNR。iSNR和oSNR可分别定义为

(5)

(6)

(7)

由式(4)可知，通过设计滤波器可以提高阵列的SNR，抑制噪声信号，增强输出的语音信号，因此，要求式(4)的值应该远大于1；若式(4)的值小于1，表明输出信噪比小于输入信噪比时，表明系统的噪声系数大，需要对其进行抑制。本文考虑引入白噪增益指标来判定阵列的SNR能力。

根据文献[13]，如果噪声在时间域和空间域上都是白噪声，则Γv=IM，其中IM为单位矩阵。此时，SNR增益称为白噪增益，其定义为：

(8)

本文考虑在研究均匀圆形麦克风阵列的基础上，提出一种基于二阶差分圆形麦克风阵列进行白噪增益最大化的设计方法，该方法首先引入二阶差分麦克风阵列到均匀圆形麦克风阵列中，接着通过设计滤波器系数，使得白噪增益最大化。

3 基于最大白噪增益的二阶差分波束形成器设计

L阶输出的DMA阵列如图2所示，阵列以级联的方式输出，第一阶输出为两个相邻阵元相减得到，第二阶输出为两个相邻的第一阶输出相减得到，同理得到第L阶输出是由两个相邻的第L-1阶输出相减得到。在DMA中，阵元数决定了阵列的输出阶数，故M个阵元可以得到L=M-1阶输出。

图 2 DMA输出框图

根据图2，结合式(2)，假设DMA中各级级联的滤波器系数为hDMA(ω)：

hDMA(ω)= [H1(1)(ω),H2(2)(ω),…,HM(L)(ω)]

(9)

结合式(3)与式(6)，可得DMA阵列在期望方向θ处的波束方向图可表示为：

(10)

为了得到DMA在期望方向θ上L阶的频率不变的方向图输出，可以把式(7)改写为：

(11)

其中，αL,l,l=1,2,…,L表示DMA的第L阶输出模式上加入空值的个数 ，αL,l的取值不同DMA会产生不同的输出波束模式如：心形、超心形和超指向性心形等。根据文献[10]，DMA期望方向θ上的值为

BL(θ)=cosθ

根据式(8)，L阶DMA在任何模式下的期望方向上至多具有L个空值，由于cosθ是一个偶函数，因此在极坐标系下波束图是关于x轴对称，可以只考虑期望角度θ∈[0，1800]。因此把圆形阵列的白噪增益引入到DMA中，根据式(5)可以得到DMA经过L阶级联后，阵列的白噪增益可表示为：

(12)

由式(9)可知，DMA中阵列白噪增益受信号频率的影响，当阵列接收的信号频率较低时，系统的WNG也随之降低。为了使差分阵列获得最大的白噪增益，从而提高阵列输出SNR，研究了以下两种设计方法：

首先，本文考虑DMA指向期望方向θ，且最大化WNG的L阶DMA波束图设计，其数学上可表示为：

(13)

其中，α=[cosθ,αL,l,…,αL,L]和D(ω,α)表示DMA阵列的方向导向向量矩阵，其可表示为：

(14)

根据文献[17]，采取最小范数求解式(10)得到的权值函数hMWNG：

hMWNG=DH(ω,α)[D(ω,α)DH(ω,α)]-1α

(15)

当DMA高阶输出(即L>3)时，加入的空值比较多，即使DMA接收的信号频信号较低，波束方向图的效果仍然较好。但当L≤2时，DMA输入的空值比较少，此时如果DMA接收到低频信号时，则波束方向图的效果很不理想。

hMWNG1(ω)=h′DMA(ω)h″MWNG(ω)

(16)

假设DMA阵列始终在无失真的条件下，因此满足如下的关系：

dH(ω,cosθ)h′DMA(ω)h″MWNG(ω)=1

(17)

(18)

于是，在最大化WNG时，且使期望方向θ在无失真条件下的优化模型可表示为：

(19)

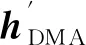
由式(19)求解出DMA的二阶段滤波器的第二阶输出的权值函数为：

(20)

联合式(18)与式(20)，基于最大化白噪增益的二阶段滤波器的波束响应为：

(21)

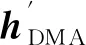
4 仿真验证

选取半径分别为r=1 cm和r=4 cm，阵元为M=4的均匀圆形DMA，期望方向θ=00，DMA二阶输出在该方向上加入2个空值。比较采用最小范数的方法求解的DMA权值向量hMWNG和基于最大白噪增益在两阶滤波的方法求解的DMA权值向量hMWNG1。在仿真中，DMA和MWNG分别表示DMA的权值向量函数为hMWNG和hMWNG1的波束形成器。分别比较两种不同的方法获得DMA的权值向量的WNG和期望波束方向图。

图3给出了阵元为M=4的均匀圆形DMA半径r=1 cm和r=4 cm在不同信号频率下的阵列的白噪增益结果图。

由图3可知，权值向量函数hMWNG的DMA在f=1.4 kHz是阵列白噪声增益异常，而本文设计的最大白噪增益异常点在f=0.3 kHz。通过比较，本方法设计的波束形成器可以提高阵列在处理低频信号的能力，增大了阵列在低频信号处理的稳健性。且本文设计的波束形成器在其他采样频率上的白噪增益远大于权值向量函数hMWNG的DMA，因此本文设计的波束形成在白噪增益上性能更好。

图 3 阵列白噪增益

图4、图6、图8和图10半径r=1 cm 信号频率分别为：0.8 kHz、2 kHz、4 kHz和7 kHz下的期望方向均在0°方向上波束方向图。

图5、图7、图9和图11半径r=3 cm信号频率分别为：0.8 kHz、2 kHz、4 kHz和7 kHz下的期望方向均在0°方向上波束方向图。

图 4 r=1 cm，f=0.8 kHz的波束图

图 5 r=4 cm，f=0.8 kHz的波束

图 6 r=1 cm，f=2 kHz的波束图

图 7 r=4 cm，f=2 kHz的波束图

图 8 r=1 cm，f=4 kHz的波束图

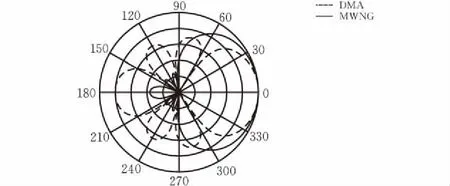
图 9 r=4 cm，f=4 kHz的波束图

图10 r=1 cm， f=6 kHz的波束图

图11 r=4 cm，f=6 kHz的波束图

由仿真图可以看出，本文MWNG波束形成器在采样频率低时依旧有效，而DMA波束形成器在采样频率低时随着白噪增益的异常而波束方向图失真，在仿真图可以看出，采用DMA波束形成的方法得到的波束图不能够保证频率不变的特性，波束图在各个采样频率上有少许变化，而采用MWNG的方法的波束形成器得到的波束方向图保持了频率不变的特性，MWNG的波束形成的主瓣远比DMA波束形成大，因此阵列的信噪比增益远大于DMA波束形成器。仿真图表明在阵元间距变大时，波束形成器处理信号的能力都会变差，通过比较最大白噪增益的波束形成器的适应能力远大于传统DMA波束形成器。

5 结论

在差分麦克风阵列中，常常会因为信号采样频率低，而造成阵列的白噪增益异常的问题，进而影响阵列性能的现象，本文提出了一种基于最大白噪增益的波束形成器，通过仿真结果，得到如下结论：

1)通过本文的方法可以较好改变白噪增益在信号采样频率低异常的问题，提高了阵列的工作频率范围，同时增大了阵列的信噪比。

2)本文方法实现了频率不变的方向图输出，本文的频率不变方向图的范围提高了约1 kHz。

3)相较于采用最小范数求解权值向量的方法的DMA，本文方法提高了阵列波束图的主瓣级，降低了旁瓣区域，从而提高了阵列的性能，增加了阵列处理信号的能力。本文方法仅改变阵列输出模式，并没有从结构上改变差分麦克风阵列，此方法设计波束形成器容易实现，具有较好的经济利用价值。