对数平均数不等式的证明与应用

安徽省合肥一六八中学 (230000) 谈世勇

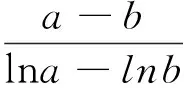
1.对数平均不等式的代数证明

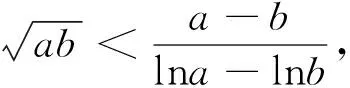
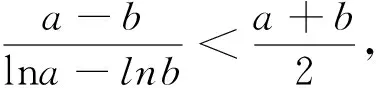
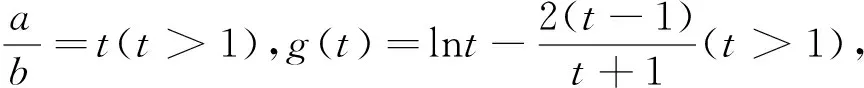
该不等式本身的证明是通过构造函数，借助于导数作为工具，利用函数单调性而得．在处理某些与指数、对数相关的不等式问题时，可以尝试应用它来帮助思考分析．

2.对数平均数的不等关系的几何证明

图1 图2

因为S曲边梯形ABQP>S梯形ABFE=S矩形ABNM，

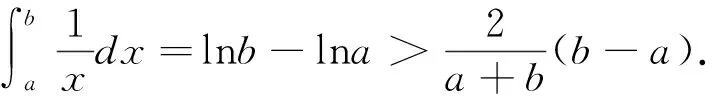
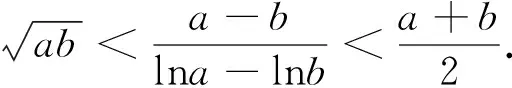
3.对数平均数不等关系的应用举例

例1 (2010年天津高考理科21题)已知函数f(x)=xe-x(x∈R)．

(Ⅰ)求函数f(x)的单调区间和极值；

(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称，证明：当x>1时，f(x)>g(x)；

(Ⅲ)如果x1≠x2，且f(x1)=f(x2)，证明：x1+x2>2．

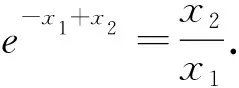
例2 (2011年辽宁高考理科压轴题)已知函数f(x)=lnx-ax2+(2-a)x．

(1)讨论函数f(x)的单调性；

(3)若函数y=f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：f′(x0)<0．