一个开放问题的探究
2020-05-30 04:07江苏省姜堰中等专业学校225500
中学数学研究(江西) 2020年4期
江苏省姜堰中等专业学校 (225500) 陈 宇
已知a,b,c∈R+,当λ与μ满足什么条件时,如下不等式成立:
笔者将主要依据分类,换元,特殊化与一般化及排除等思想方法解答这个问题.
解:由不等式(1)成立,可知μ+λ>0,则λ与μ存在下列四种关系:
(1)μ≥λ>0,(2)μ>0≥λ,(3)λ>μ≥0,(4)λ>0>μ.
当a=b=c>0时,不等式(1)成立,只需μ+λ>0,与μ,λ的大小无关.
当a,b,c不全相等时,∵不等式(1)两边循环对称,不妨设0 同理,当λ=0时,有μ>0. 当λ,μ>0时,不等式(2)显然成立,从而μ+λ>0,且与μ,λ的大小无关. 当λ<0时,不等式(2)有解集当且仅当Δ=4(μ+λ)(μ-λ)>0⟹μ>0>λ. 当λ>0,μ<0时,不等式(2)有解集,则Δ=4(μ+λ)(μ-λ)<0⟹μ<0<λ. 依次对应取m=a,b,c,n=b,c,a即得 ∵当x>1,y≥1时,有(x6y4-1)+x2y2(x2y2-1)+2xy(x4y3-1)>0,从而(4)不成立.故λ>μ>0时不等式(3)不成立. 若λ>μ=0,由上可得λ[(x6y4-1)+x2y2(x2y2-1)]=0同样矛盾. 当λ>0,μ<0时,-2xy(1-x4y3)= 综上可知:不等式(1)成立. ①当且仅当正实数a=b=c时,等号成立.此时,λ与μ满足条件μ+λ>0; ②正实数a,b,c不全相等时,(ⅰ)λ与μ满足条件μ+λ>0,且μ≥λ>0;或μ>0≥λ;(ⅱ)λ=2μ>0. 笔者能力所限,只能求出本文所列“μ与λ满足条件”.期待有兴趣的读者给出更宽的条件.







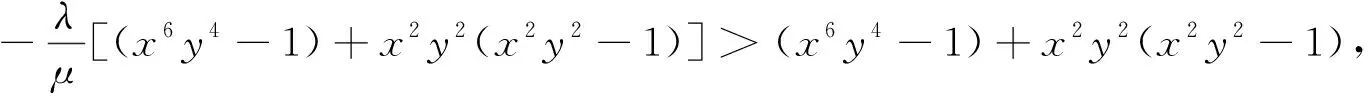


猜你喜欢
中学数学研究(广东)(2022年9期)2022-06-16
中小学校长(2021年9期)2021-10-14
中等数学(2021年5期)2021-08-14
阅读(书香天地)(2021年2期)2021-04-06
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27
中学生数理化(高中版.高考数学)(2019年9期)2019-09-27
中学生数理化(高中版.高二数学)(2018年11期)2018-11-29
新高考·高一数学(2018年1期)2018-11-23
新高考·高一数学(2018年2期)2018-11-20

