基于R语言探求圆周率的估计值

李海

【摘 要】估算圆周率一直以来都是数学研究者感兴趣的话题。本研究利用R语言，运用已知的数学关系，设计常用的计算机模拟思路，估算π值，以探讨圆周率的多种可行性估算方法，以期启发、训练R语言编程思维。

【关键词】R语言;实验;圆周率

【中图分类号】G642  【文献标识码】A  【文章编号】1671-8437（2020）04-0229-02

在小学阶段学习圆的相关知识时，必然会提及圆周率，随着进一步的学习，发现有关圆周率π的学习几乎贯穿了整个受教育过程，涉及的学科和用途也是十分广泛。π取自希腊语，表示圆的周长与直径的比值。历史上，许多中外数学家都试图寻求圆周率π的近似值，而中国数学家刘徽和祖冲之采用几何法也分别对圆周率进行过估算，得出圆周率π的估计值，并一步一步将精确位数提升。2019年3月，谷歌利用现有计算机技术将圆周率精确到小数点后31.4万亿位。当然也有很多民间数学爱好者借助计算机软件技术来估算圆周率值，唐永鸽[1]用office办公软件excel、程登彪[2]和周辉[3]则利用数学软件mathematica分别对圆周率进行估算。

R语言作为一个自由、免费、源代码开放的软件，是一个用于科学绘图和统计计算的优秀工具[4]。该软件将数学思维与计算机程序设计重要思想完美结合。采用R语言软件，根据不同数学估算公式估计圆周率的值，最终以图形的方式呈现。

1   估算方法

1.1  “划分网格”估算法

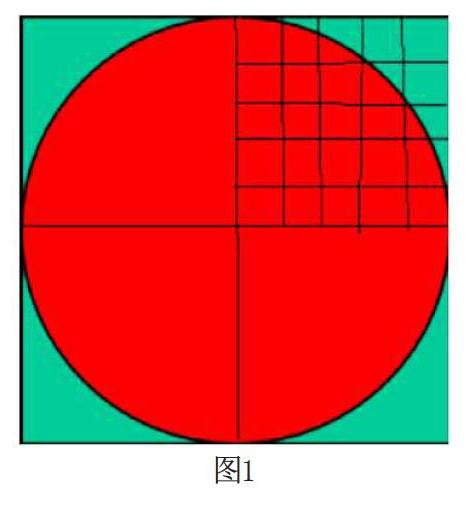
“划分网格”估算法：此方法类似著名的蒙特卡罗法，不同的是将正方形分成n2个小正方形，统计落在内接圆内的小正方形个数占所有正方形的比例，利用四分之一个圆来研究，看落入其中的小正方形有多少个，并计算概率，再用概率反推π的值，即π=4N/n2（N表示落入单位圆内小正方形的个数），如图1所示。

通过计算机模拟，运行下列程序：

mianji=function（n）{

kk=matrix（0，n，n）

o=1/n

for（x in 1：n）{

for（y in 1：n）{

zb=c（x*o，y*o）

kk[x，y]=ifelse（sqrt（sum（zb^2））<=1，1，0）

}

}

sum（apply（kk， 1， sum））/n^2*4

}

pi=rep（0，1000）

for（s in 1：1000）{

pi[s]=mianji（s）}

plot（1：1000，pi，ylim = c（2.5，4））

abline（h=3.14，col=2）

随着n的变大，π的值越趋于稳定，如图2：

1.2  “三角形”估算法

“三角形”估算法：利用已证明的结论，任意写两个小于1的数（x，y），将它和1组成一个数对（x，y，1），则由x、y和1作为线段长度，能构成一个钝角三角形的概率为P=（π-2）/4。利用计算机选取1到1000的随机数，并计算此概率，并反推π值，即π=4P+2。通过R软件运行如下程序：

pi=rep（0，1000）

for（s in 1：1000）{

i=rep（0，10000）

for（j in 1：10000）{

bianchang=runif（2，0，1）

i[j]=ifelse（sum（（bianchang）^2）<1&&sum（bianchang）>1，1，0）

}

pi[s]=4*mean（i）+2

}

plot（1：1000，pi，ylim = c（2.5，4））

abline（h=3.14，col=2）

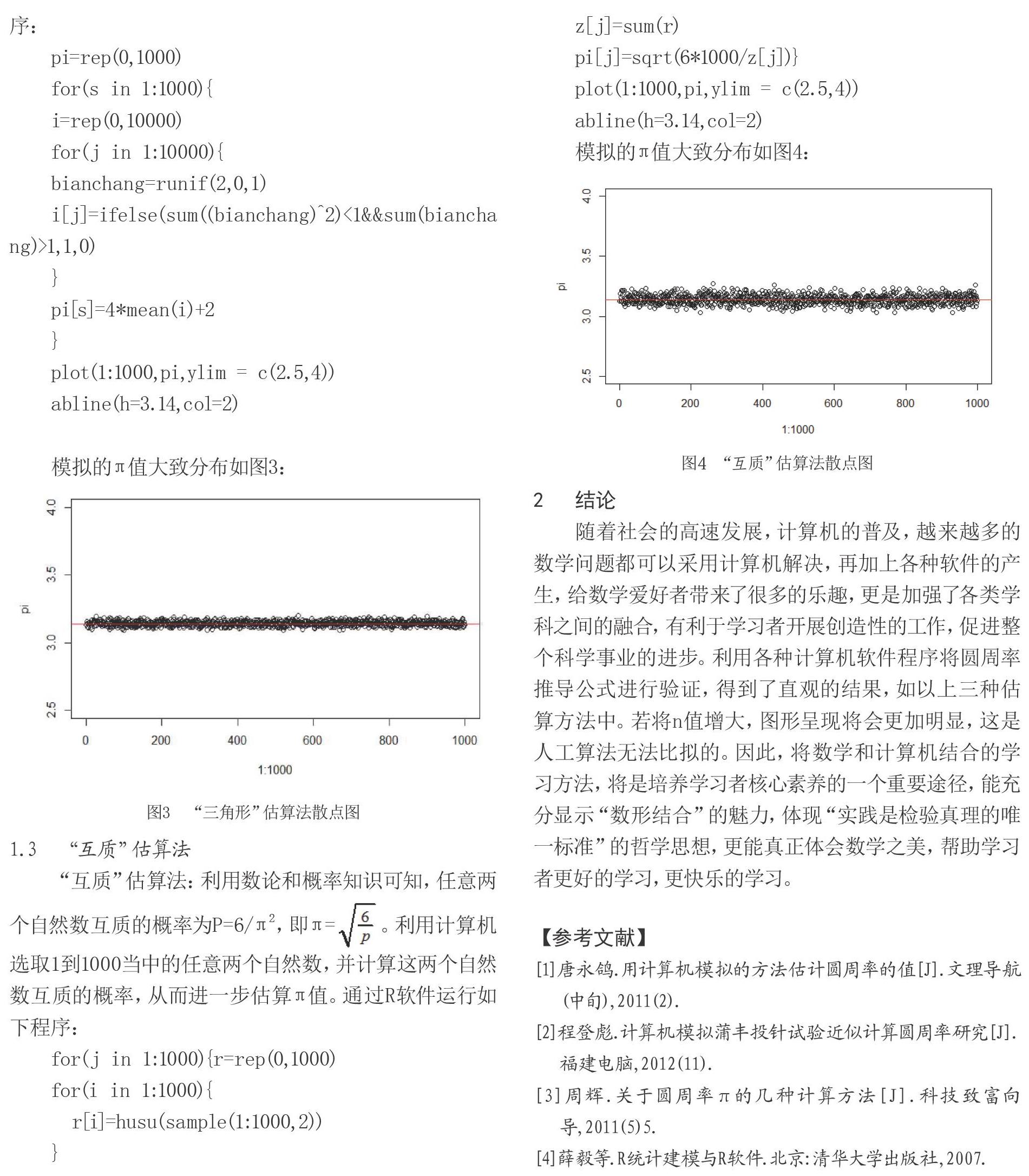
模拟的π值大致分布如图3：

1.3  “互质”估算法

“互质”估算法：利用数论和概率知识可知，任意两个自然数互质的概率为P=6/π2，即π=。利用计算机选取1到1000当中的任意两个自然数，并计算这两个自然数互質的概率，从而进一步估算π值。通过R软件运行如下程序：

for（j in 1：1000）{r=rep（0，1000）

for（i in 1：1000）{

r[i]=husu（sample（1：1000，2））

}

z[j]=sum（r）

pi[j]=sqrt（6*1000/z[j]）}

plot（1：1000，pi，ylim = c（2.5，4））

abline（h=3.14，col=2）

模拟的π值大致分布如图4：

2   结论

随着社会的高速发展，计算机的普及，越来越多的数学问题都可以采用计算机解决，再加上各种软件的产生，给数学爱好者带来了很多的乐趣，更是加强了各类学科之间的融合，有利于学习者开展创造性的工作，促进整个科学事业的进步。利用各种计算机软件程序将圆周率推导公式进行验证，得到了直观的结果，如以上三种估算方法中。若将n值增大，图形呈现将会更加明显，这是人工算法无法比拟的。因此，将数学和计算机结合的学习方法，将是培养学习者核心素养的一个重要途径，能充分显示“数形结合”的魅力，体现“实践是检验真理的唯一标准”的哲学思想，更能真正体会数学之美，帮助学习者更好的学习，更快乐的学习。

【参考文献】

[1]唐永鸽.用计算机模拟的方法估计圆周率的值[J].文理导航（中旬），2011（2）.

[2]程登彪.计算机模拟蒲丰投针试验近似计算圆周率研究[J].福建电脑，2012（11）.

[3]周辉.关于圆周率π的几种计算方法[J].科技致富向导，2011（5）5.

[4]薛毅等.R统计建模与R软件.北京：清华大学出版社，2007.