中考压轴题之一

摘 要：初中数学中的圆，是我们日常生活中随处可见的几何图形，学生们在平时的学习和生活中具有一定的了解，但圆这一部分知识又是初中各类考试中的难点，得分率比较低，学生难以掌握。另外，圆是中考中的常见综合压轴题，但常常因为圆形的隐蔽性、综合性、复杂性。让学生很难想到破解思路，现归纳三种常见的类型，供广大师生朋友参考。

关键词：中考;压轴题;圆;方法

方法一：“找定点、寻定长、现圆形”。

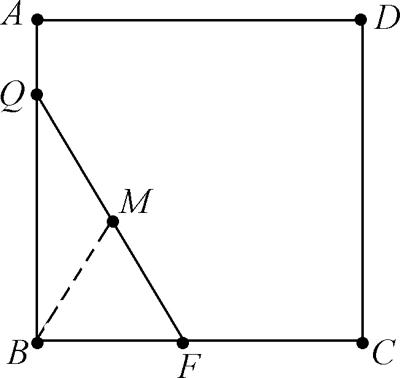
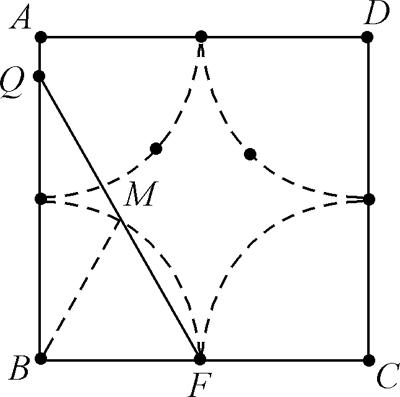
【例1】 如图，正方形ABCD的边长为2，将长为2的线段QF的两端放在正方形相邻的两边上同时滑动，点Q从A出发，沿ABCDA逆时针方向滑动到A为止，同时点F从B出发，也沿BCDAB逆时针方向滑动到B为止，那么在这个过程中，线段QF的中点M经过的路线围成的图形的面积为    。

分析：线段QF的长度始终是2，连接BM，则在Rt△QBF中，BM=12QF=1，所以点M应该在以点B为圆心的圆弧上运动。同理当点Q、F分别在其他边上运动时，点M均在一个四分之一圆弧上运动，故最终点M总的运动路径如图所示，线段QF的中点M经过的路线围成的图形的面积为4-π。

方法二：“见直角，想直径，定外心，现圆形”

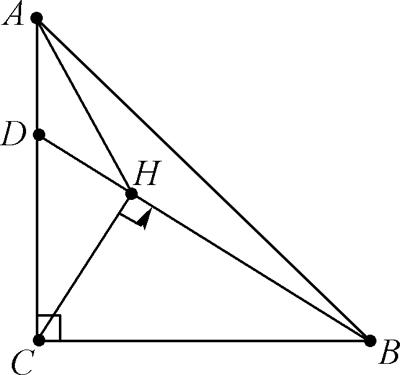
【例2】 如图，在等腰△ABC中，∠ACB=90°，AC=BC=4，D为线段AC上一动点，连接BD，过点C作CH⊥BD于点H，连接AH，则AH的最小值为    。

分析：当点D在运动时，∠CHB=90°始终保持不变，所以点H始终在以线段BC的中点O为圆心，线段OB为半径的圆弧上运动。因此，连接AO交圆弧于点H，此时AH有最小值为25-2。

方法三：“见定角，找对边，想周角，转圆心，现圆形”

【例3】 如图，在边长为23的等边△ABC中，动点D、E分别在BC，AC边上，且保持AE=CD，连接BE，AD，相较于点P，则CP的最小值为    。

分析：根据△ABE≌△CAD，可得∠1+∠2=60°，得∠APB=120°，且保持不变。故可知点P在以點O为圆心，线段OP为半径的圆弧上运动，当点O、P、C三点在同一条直线上时，有CP的长度最小值为2。

通过上述解法的分析，希望同学们在碰到类似的圆形几何题目时，去关注题中是否有“定长”“直角”或“定角”，并且联想起上述方法。通过多做多练此类型的题目，相信再碰到圆的类似问题时，同学们就多了一种思路，不至于无从下手，摸不着思路。

但是数学这门学科是一门灵活的学科，我们对学习方法不能一味地死记硬背，而是要在掌握数学方法的基础上进行灵活应用，做到融会贯通，不断培养仔细活跃的数学思维和严密的推理能力，才能更好地学好数学。

作者简介：

何登，浙江省慈溪市，慈溪阳光实验学校。