基于Legendre-Fourier-Galerkin谱方法求解薛定谔方程
(云南财经大学统计与数学学院 云南 昆明 650221)
本文我们主要研究薛定谔方程,薛定谔方程分为带有时间方向的初边值问题以及不带时间方向的初边值问题,我们将针对在极坐标系下的薛定谔方程设计算法.下面首先介绍带有时间方向的二维薛定谔方程在极坐标下的初边值问题:
(1)

我们设计基于Legendre-Fourier-Galerkin(LFG)谱方法求解上述问题.
一、Fourier谱方法降维过程
假定未知函数φ=φ(r,θ,t)有如下傅里叶展开式:
(2)
其中N为给定正整数,展开式中基函数eimθ满足如下正交性质:
(3)
当整数m≠n时,δmn=0;当整数m=n时,δmn=1,γ为常数.
将(2)式代入(1)式中有:
(4)
我们利用基函数eimθ的正交性,用e-inθ同时乘以(4)式的两端,并在区间[0,2π]上对θ求积分,整理可得:
(5)
这一过程通过傅里叶变换将二维含时薛定谔方程转换为一维含时薛定谔方程,目的在于减少计算量.
二、Legendre-Galerkin谱方法多项式展开
假设-1=x0 结合LGL quadrature结点构造在r方向上的结点,将径方向r的取值范围转换到区间[-1,1]上,即: (6) (7) 将(6)式代入(7)式,并将v(r)依次换成 可得到如下解析式: (8) 此时,方程只剩下时间变量. 在时间方向上我们采用Crank-Nicolson方法离散(8)式,即 (9) 其中 其中p=0,1,2,….(迭代次数,自行选择). 设用向前的欧拉公式可以得到: 如此反复进行得: 本文通过求解具体例子来详细介绍基于基函数φi(x),eimθ的Legendre-Fourier-Galerkin 谱方法在薛定谔方程初边值问题的求解实现过程:先假定方程中的未知函数能够用基于基函数φi(x),eimθ的展开式来逼近,然后将该未知函数的逼近展开式代入方程之中,再利用LFG 谱方法得到关于未知函数的微分方程组的初边值问题和边值问题,最终通过求解该薛定谔方程的近似解的信息。 基于基函数φi(x),eimθ的LFG谱方法具有精度高、实现过程简单等优点, 本文的算法实现过程及数值例子显示了该谱方法的这些优点。所有的计算结果都通过我们撰写的Matlab程序得到。在将来我们将讨论如何利用LFG谱方法求解含有更为复杂势能场的薛定谔方程的求解问题,给研究薛定谔方程现象的物理学家提供更为精准的数值解。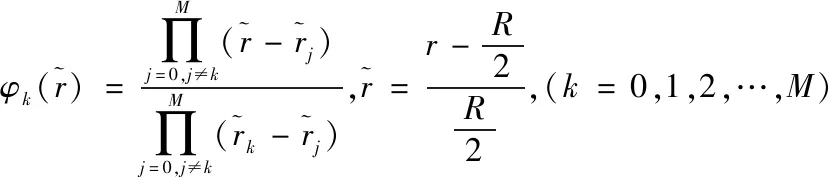


三、时间方向使用Crank-Nicolson方法


