基于深度学习的地铁短时客流量预测

(华南理工大学土木与交通学院， 广东广州510641)

0 引言

随着轨道交通的迅猛发展，地铁逐渐成为一种不可缺少的通勤方式。随着地铁客流的逐渐增加，地铁客流量也呈现出一定的时间特性，平峰时期与高峰时期的客流量存在着较大的区别，并且高峰时期部分地铁站人流相对拥挤。因此，为了满足不同时期客流的需求，合理配置地铁运力，以及制定客流高峰情况下的紧急疏散方案等，需要有效、准确地对短时间内地铁客流量的变化进行预测。

对于交通流量及客流量等交通数据的预测，较为常用的方法有两类，一类是传统统计学方法，另一类是基于计算机学习的智能计算方法，如神经网络等[1]。传统统计学方法在时序数据预测中较为常见，如卡尔曼滤波模型[2]、ARIMA模型[3]、SARIMA模型[4]等。这类模型易于操作、相对简单。但是，不同时段的地铁进站客流量是波动变化的，而传统的统计学方法大部分都受到线性假设的限制。目前应用较多的机器学习模型虽然能够解决上述问题，但是在实际环境下，这些算法容易出现因为追求预测精度导致训练时间较长，或对数据样本要求过高等问题[5]，如决策树模型[6]、支持向量机模型[7]、以及K最近邻模型[8-9]等。

随着近年来深度学习的兴起，长短期记忆网络(long short-term memory，LSTM)因为较为适合预测时序数据，从而被频繁的运用于交通流量及客流量的预测中。其中，DUAN[10]使用了LSTM模型预测行程时间，并比较了不同时间长度模型对预测误差值的影响。LIU[11]通过LSTM模型实现了对地铁客流的预测。李梅[12]则比较了LSTM、多元线性回归以及BP神经网络模型对地铁客流量预测的精度，结果表明，LSTM模型的准确性较高，并且实用价值更高。然而，LSTM模型在时序数据训练中，容易丢失部分前后时段记忆关联的信息。

地铁系统是一个复杂的系统，地铁客流量也受到多种因素的影响，而且与各因素之间的关系较为复杂，导致以影响因素为主要考虑对象的模型出现预测效果不好的情况。而时间序列预测方法一方面能够根据历史客流量的变化来对短时客流量进行预测，另一方面突出了时间因素在预测中的作用，即所有因素的综合作用体现在了时间这一因素上，使得时间序列预测方法对复杂系统的数据的预测更加有效。然而传统的时间序列预测方法受到线性假设的限制，浅层的神经网络则存在对不同时段的输入信息无记忆关联作用或者对样本数据要求较高等问题。

为了解决以上问题，本文选用能够充分考虑序列的非线性问题及可能存在不确定性问题[13]的双向长短期记忆网络(bi-directional long short-term memory，Bi-LSTM)进行预测。通过分析地铁客流量概况，发现不同星期的客流量具有不同的发展模式。根据不同星期的客流量，在深度学习的理论框架下，建立了基于Bi-LSTM的地铁短时客流预测模型，更加准确地预测不同日期的地铁客流量。

1 地铁客流量概况

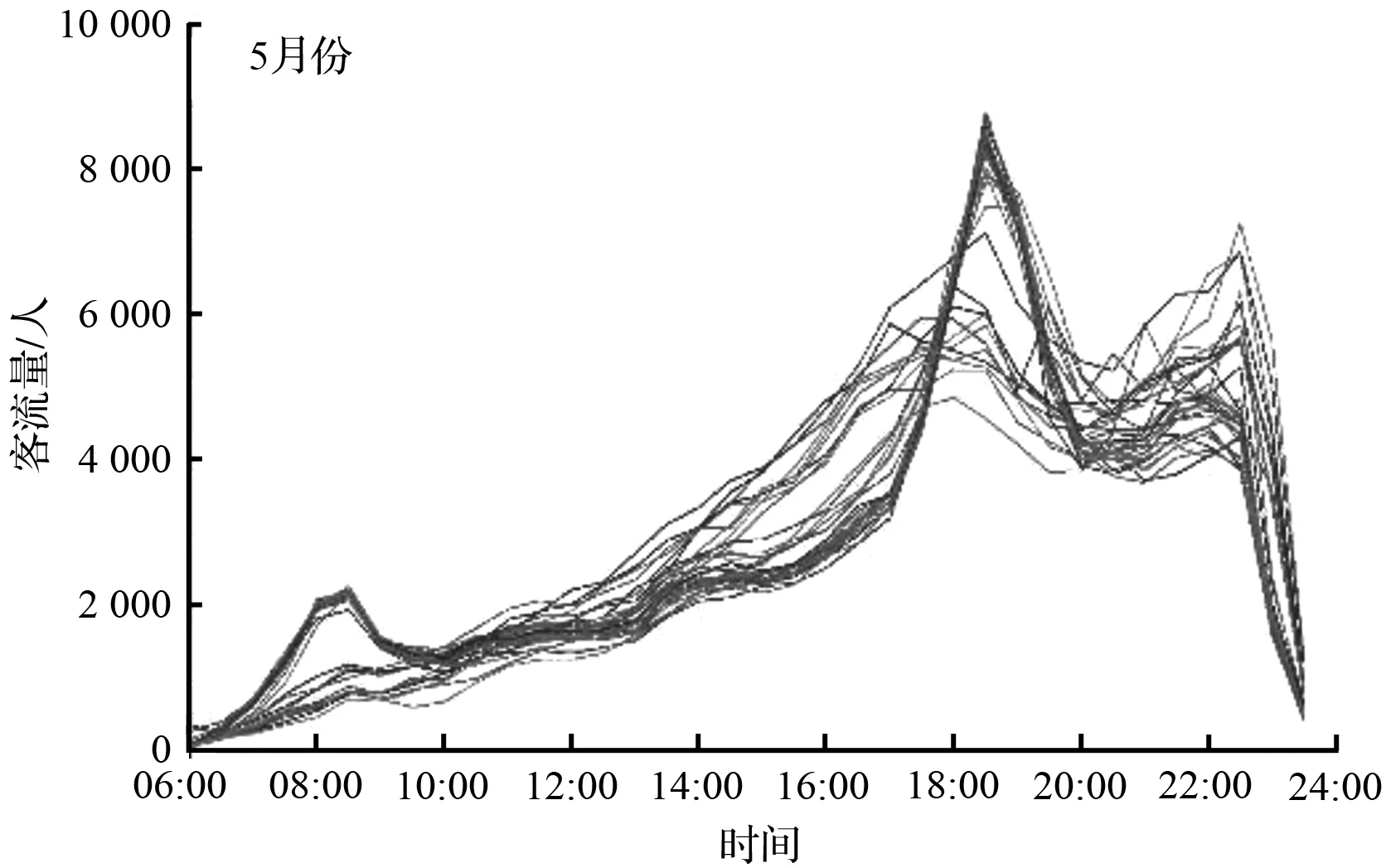
地铁出行目的主要以上班通勤和社交活动为主，其进站客流量具有一定的时间特性。以2017年5月广州市体育西路站的进站客流量为例进行分析，其中2017年5月份包含劳动节假期和端午节假期，对客流量分析存在一定的代表性。将5月份的进站客流量按时间作图，可以较为明显的发现不同日期客流量可以分为三类，如图1所示。可以发现，5月份地铁进站客流量大致走向相似，在早高峰期间基本可分为两类，但是晚高峰期间较为杂乱。同时由图1可知，地铁客流的发展模式存在一定的差别，而时间序列预测方法对于短期内客流发展模式变化较大的预测存在一定的误差，因此，需根据客流特征将不同日期的客流进行分类。

由于节假日及周末对上班通勤及社交活动客流在时间特性上相似，节假日的前一工作日与周五在时间特性上类似，因此将节假日和节假日前一工作日分别与周末和周五归为同一类。结合图1中的客流量变化情况，可以将其按照星期分为三类，周一至周四、周五以及周末。将5月份的客流量根据星期进行分类后可以发现，周一至周四的进站客流量重合度较高。相比于其他工作日，周五存在两个晚高峰，周末的地铁客流则主要是不存在早高峰阶段。根据星期分类后，可以较为明显的看到不同日期的客流量差异，且分类后客流量曲线重合度较高。

(a) 5月份总客流量序列

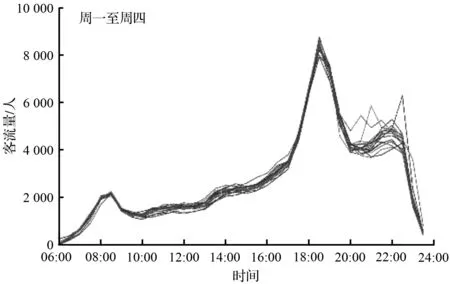
(b) 五月份中周一～周四客流量序列

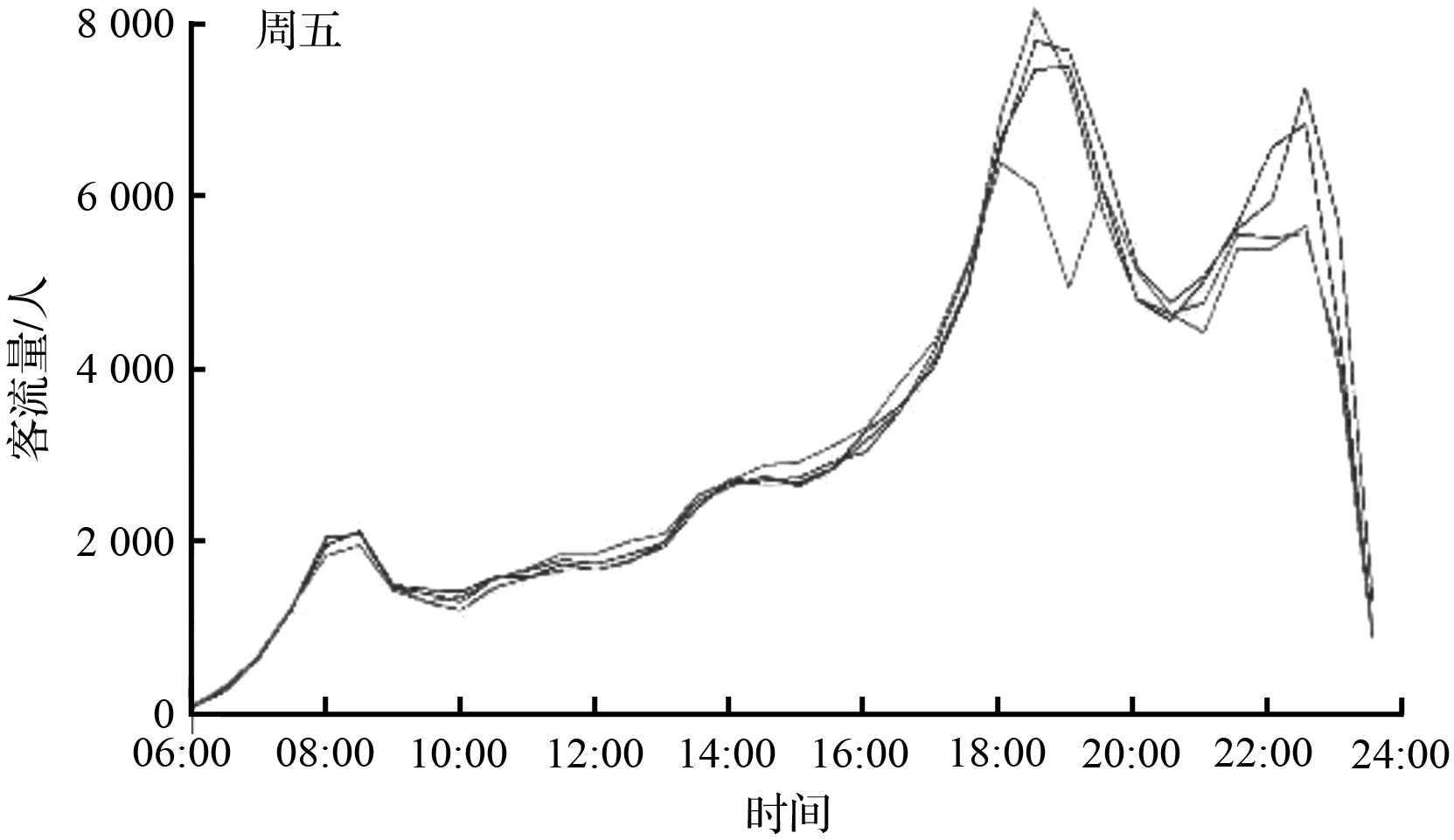
(c) 5月份中周五客流量序列

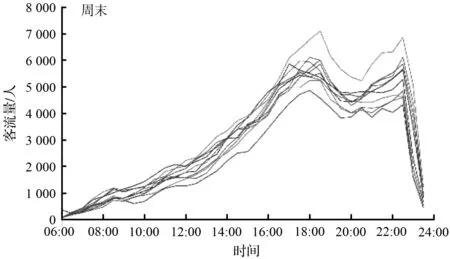
(d) 5月份中周末客流量序列

图1 5月份客流量时间序列
Fig.1 Passenger time series of May

因为工作日期间，上班通勤客流为主要客流；休息日期间，非通勤客流为主要客流。对于上班通勤的客流而言，周一至周四的时间特性类似，均为正常工作上班；周五由于接近休息日，部分乘客在下班后选择其他社交活动，从而地铁客流出现第二个晚高峰；周末通勤客流减少，非通勤客流增加，所以与工作日期间的进站高峰期在流量及出现时间上存在一定的不同。

2 模型

2.1 循环神经网络

深度学习中有两种模型较为常用：前馈神经网络(feedforward neural network，FNN)和循环神经网络(recurrent neural network，RNN)。与普遍使用的FNN相比，RNN对前面时段的输入信息具有记忆功能，并可以对输出结果产生影响，即RNN模型中，不同时段的输入数据是可以产生相互影响的，因此RNN对于时序数据的处理非常有效。RNN的网络结构及其展开图如图2所示。其中xi为第i时刻的输入数据，yi为第i时刻的输出数据，hi为第i时刻的记忆数据。由于hi与i-1时刻的记忆值hi-1相关，从而对之前的信息有记忆功能。

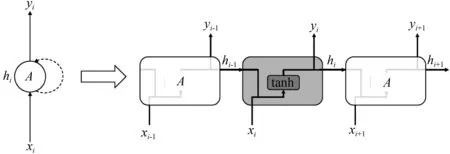
图2 RNN网络结构Fig.2 RNN network structure

2.2 长短期记忆网络

虽然RNN对之前的信息有记忆功能，但是模型在训练时存在梯度消失的情况，从而出现长期依赖问题，即在时间间隔不断增大时，RNN对较远的信息无法连接。因此，长短期记忆网络被提出。作为RNN的变种，LSTM解决了RNN的长期依赖问题[14]。LSTM与RNN具有相似的结构，区别在于，LSTM的隐含层中含有输入门、输出门、遗忘门以及细胞状态ct，细胞状态直接在整个链上运行，使得信息更加容易保持不变的流传下去，从而使得LSTM能够记忆较长时间的信息，其网络结构如图3所示。

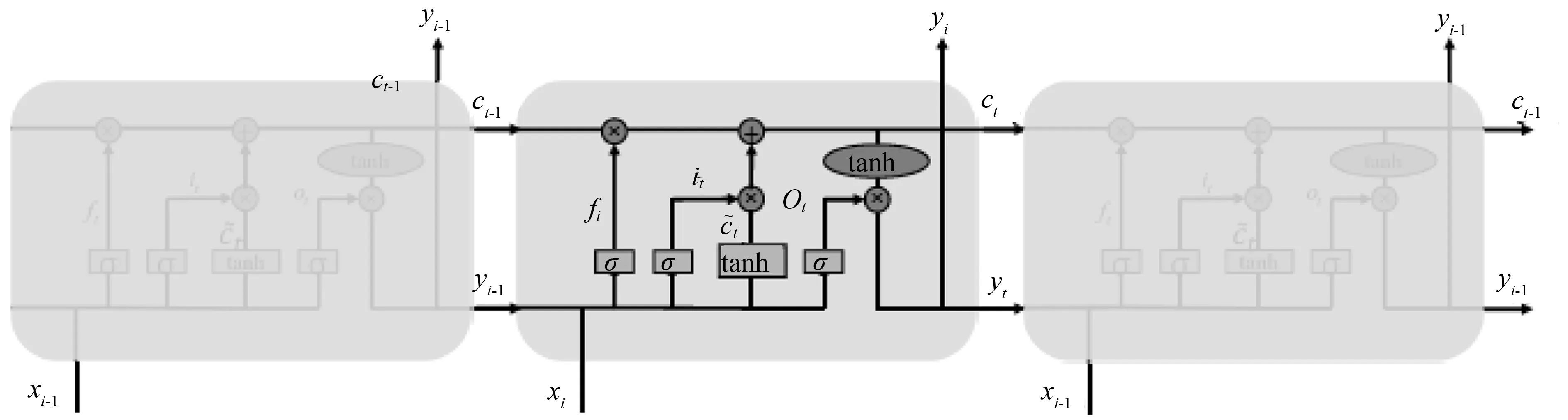
图3 LSTM网络结构Fig.3 LSTM network structure

① 遗忘门

遗忘门主要是对之前信息的选择性遗忘，选择遗忘或保留部分序列状态信息。即将上一个序列的yt-1和当前序列的xt作为输入，通过sigmoid激活函数，决定上一层的细胞状态ct-1需要遗忘以及需要保留的信息，如图4所示，函数表达式为：

ft=σ(Wf·[yt-1,xt]+bf)。

(1)

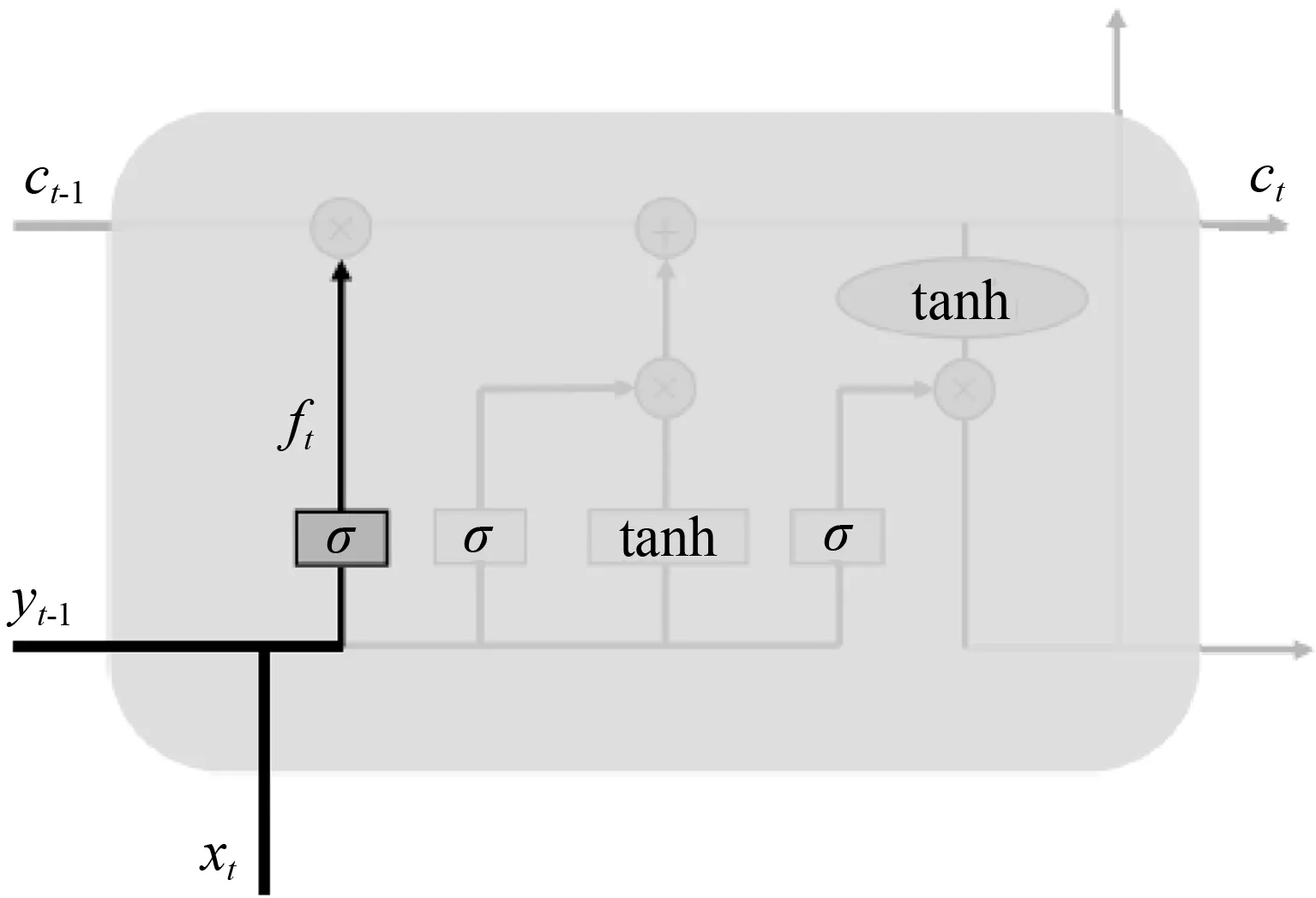
图4 遗忘门结构Fig.4 Structure of forget gate

② 输入门

输入门的信息包括上一个序列的细胞状态、当前序列输入信息以及上一个序列的输出信息，通过这些信息更新新的细胞状态。新的细胞状态更新主要包含两个部分，一个是根据遗忘门决定上一个序列的细胞状态ct-1要保留及遗忘的信息，另一个是将当前序列的信息加入到细胞状态中去，即，使用tanh函数产生一个新的向量，如图5(a)所示。然后将两个部分相加组成当前序列下的细胞状态ct，如图5(b)所示。函数表达式为：

it=σ(Wi·[yt-1,xt]+bi)，

(2)

(3)

(4)

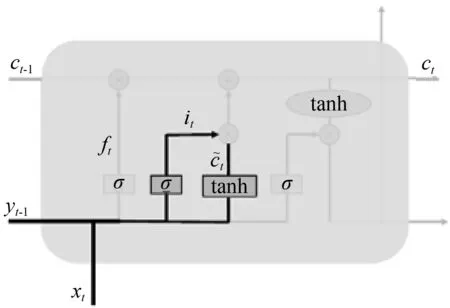
(a) 当前序列信息处理

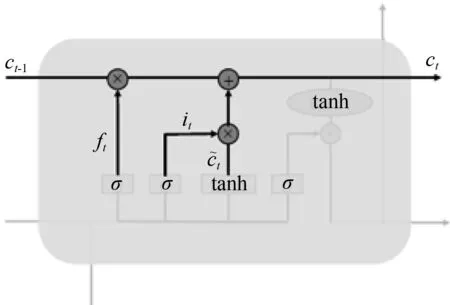
(b) 细胞状态Ct更新

图5 输入门结构
Fig.5 Structure of input gate

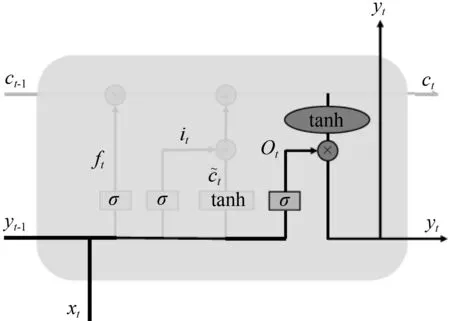
图6 输出门结构Fig.6 Structure of output gate

③ 输出门

输出门通过输入信息、上一序列输出信息以及细胞状态来输出当前序列信息。输出门基于当前序列的细胞状态ct来决定输出结果，通过tanh函数对细胞状态ct进行处理，并且根据sigmoid函数选择输出的内容，如图6所示，函数表达式为：

ot=σ(Wo·[yt-1,xt]+bo)，

(5)

yt=ot·tanh(ct)。

(6)

2.3 双向长短期记忆网络

部分时段的数据预测不仅受到前面时段的影响，后面时段的变化也同样能够影响当前时段的数据，同时通过前面时段和后面时段数据一同训练预测，会使预测结果更加准确，因此，出现了双向长短期记忆网络，结构图如图7所示，输出层由前向层和后向层共同决定，函数表达式为，

ht=f(w1xt+w2ht-1)，

(7)

(8)

(9)

图7 双向网络结构Fig.7 Bi-directional network structure

3 地铁客流量预测模型框架

3.1 地铁客流量时间序列

城市地铁的运营模式通常为白天运行，夜间维护。因而，在夜间进站客流量都将为0，通常的做法是根据固定线路的首末班车时间，确定运行时间区间，设置半小时为时间间距，分别统计不同时间段进站客流量，如式(10)所示，i为样本日期的时间序列编号，m为样本数据的天数，n为每天的时间间距数，i∈[1,m]。

Xi=(xi,1,xi,2,…,xi,n)。

(10)

提取不同日期的客流量时间序列后，根据周一至周四、周五及周末来分类，分别得到数据库集Z1、Z2、Z3，以数据库中无节假日且从周一开始为例，如式(11)～式(13)所示。

Z1=(X1,…,X4,X8,…)，

(11)

Z2=(X5,X12,X19,…)，

(12)

Z3=(X6,X7,X13,X14,…)。

(13)

3.2 数据标准化处理

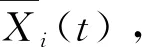
(14)

3.3 预测结果评估指标

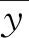
(15)

为了对模型的预测结果进行评估，本文将均方根误差(RMSE)以及平均绝对百分比误差(MAPE)作为评价指标，如式(16)、式(17)所示。

(16)

(17)

4 案例分析

本文以2017年5月广州市体育西路站的进站客流量为例，以早上6：00作为起始时间，24：00作为结束时间，时间间隔为30 min，分别提取不同时间段的刷卡进站人数。

4.1 客流量的时序序列处理

2017年5月1日和5月30日均为节假日，分别为劳动节和端午节。由于放假调休，5月27日虽然为周六，但仍是工作日。5月1日的客流量序列为历史数据库中的第1个序列，6:00～6:30的客流量为各个序列的第1个数据，即X1=(x1,1,x1,2,…,x1,36)，以此类推。因此，根据不同日期的星期数，可以得到相应的数据集Z1(周一至周四)、Z2(周五)、Z3(周末)，之后可根据预测日星期数选择相应的数据集进行训练。

Z1=(X2,…,X4,X8,…,X11,X15,…,X18,X22,…,X25,X31)，

(18)

Z2=(X5,X12,X19,X27)，

(19)

Z3=(X1,X6,X7,X13,X14,X20,X21,X28,X29,X30)。

(20)

4.2 模型参数调整

Bi-LSTM网络结构包含部分可调整参数，根据数据特点需选择不同的参数，其中主要包括时间长度、神经网络结构中Bi-LSTM层数等。其他参数的设置则相对较为常规，如控制信息遗忘的Dropout参数设置为0.1，输入层为1层，输出层为1层，Batchsize设置为1，迭代次数设置为100，优化器为“adam”，训练模型中的评估指标为RMSE。

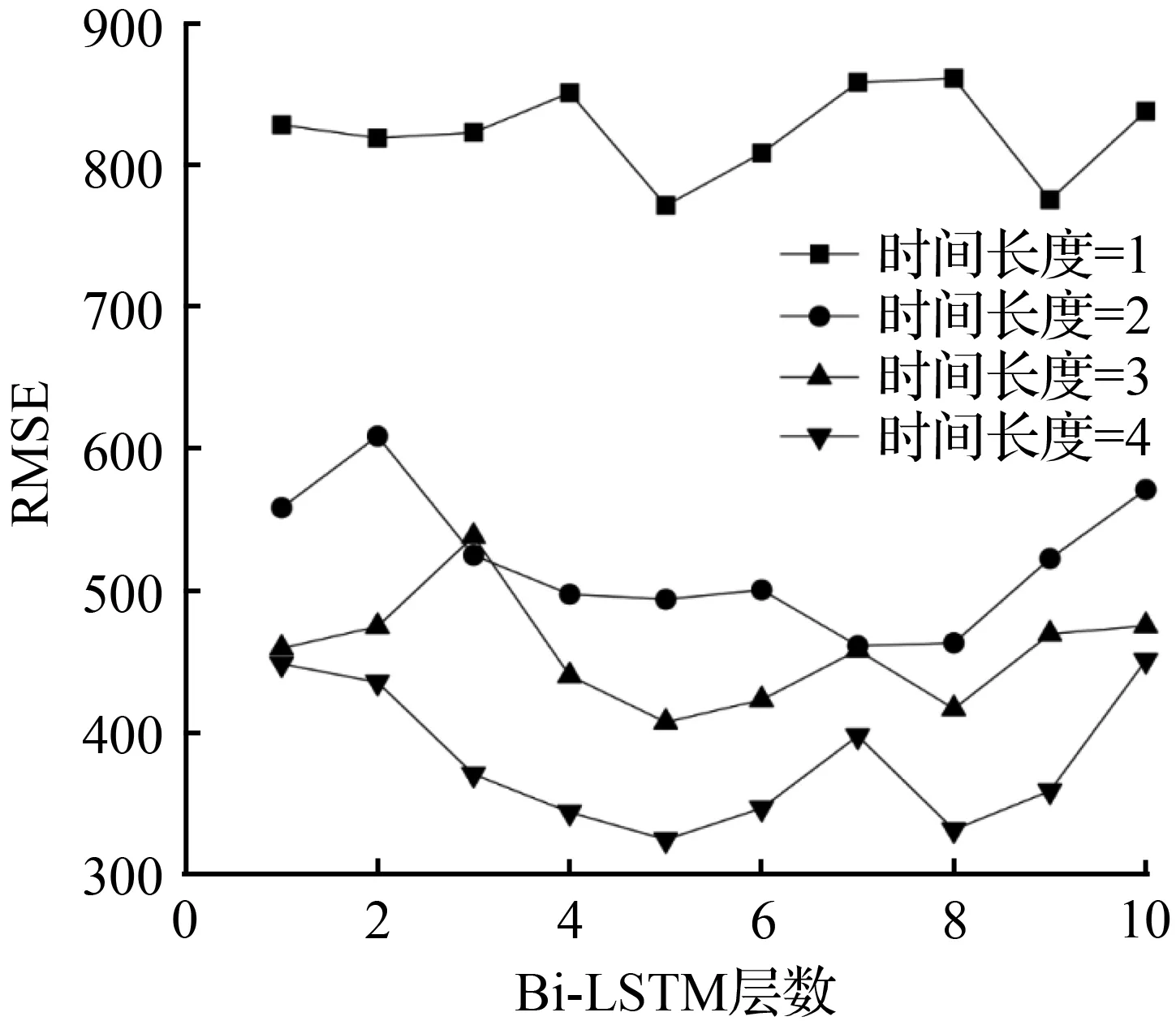
图8 参数调整结果Fig.8 Results of parameter adjustment

由第1章地铁客流概况可知，工作日期间，地铁进站客流量会出现早高峰，早高峰主要出现在7：30～9：00，峰值出现在8：30左右，而且首班列车在6：00后发车，数据的时间间距为30 min。因此，为了避免对早高峰预测的遗漏，时间长度区间设置为[1,4]。另外，神经网络结构中Bi-LSTM层数区间设置为[1,10]，结合时间长度及Bi-LSTM层数进行训练，以5月份的周一至周四数据测试为例，测试结果如图8所示。

测试结果表明，Bi-LSTM模型的时间长度参数越大，模型的效果相对越好。但是训练效果与不同的Bi-LSTM层数之间的关系则相对较为复杂，不是简单的线性关系。根据测试结果可以知道，时间长度为4，Bi-LSTM层数为5层时，训练效果最好。

4.3 预测对比模型

本文基于Bi-LSTM模型对2017年5月地铁的客流量数据进行训练，然后对2017-06-01～2017-06-04(周四～周日)的地铁客流量进行预测，并且与支持向量机算法(SVM)、决策树模型(TREE)以及长短期记忆网络(LSTM)进行预测效果对比分析。其中四种算法使用的训练数据一致，即均为根据星期分类后的数据，且LSTM算法参数与Bi-LSTM算法参数一致。下面对另外两种对比模型进行简单介绍和参数说明。

4.3.1 支持向量机模型

支持向量机(support vector machine，SVM)方法是经典的统计学习理论算法，该算法是建立在统计学中的风险最小化和VC维理论基础上的，能够较为良好的平衡模型的复杂程度及其学习能力，从而降低出现模型“过拟合”的概率[16]。SVM主要有分类以及回归两种应用。本文采用支持向量回归模型预测地铁客流量，其中模型惩罚因子C设为1。

4.3.2 决策树模型

决策树模型是经典的机器学习算法，主要用于数据的分类和预测。决策树模型通常是递归地选择最优特征，然后分割训练数据，不同的子数据集之间从而可以得到一个相对最好的分类结果。在决策树模型中，ID3、C4.5以及CART算法较为常用，但是ID3和C4.5算法的决策树分支数量较多，对噪声的处理情况不够理想，非常容易出现“过拟合”的情况。因此，本文采用CART算法对地铁客流量进行预测。

4.4 预测结果分析与比较

利用四种算法预测地铁客流量，结果如图9所示，评价指标如表1所示。可以看出，各种算法在整体的走势预测上都基本符合实际情况。对6月1日(周四)的预测，不同算法预测的结果都相对较好，基本不存在误差较大的情况。6月2日(周五)的预测情况相对不够理想，在21:00左右均有误差较大的情况出现，其中决策树模型(TREE)和长短期记忆网络(LSTM)波动情况明显。主要原因可能是训练数据相对较少，5月份中，仅有4 d的数据可供训练，导致预测结果不够理想，与实际数据相差较大。6月4日(周日)23:00的流量由于突变速度较快，客流量直接从4 816人降至了2 070人，导致预测效果均不佳。

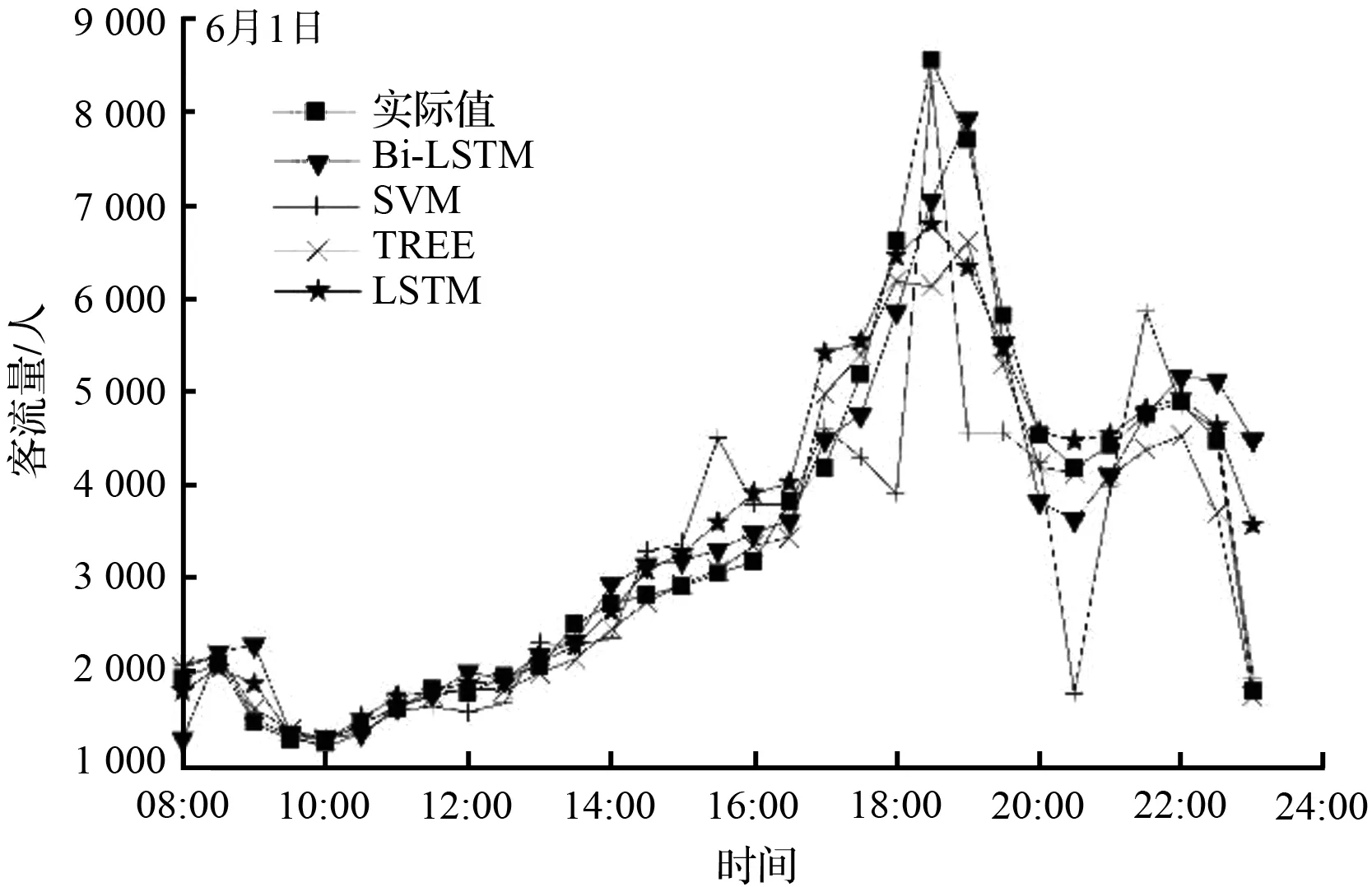
(a) 6月1日(周四)各算法预测结果比较

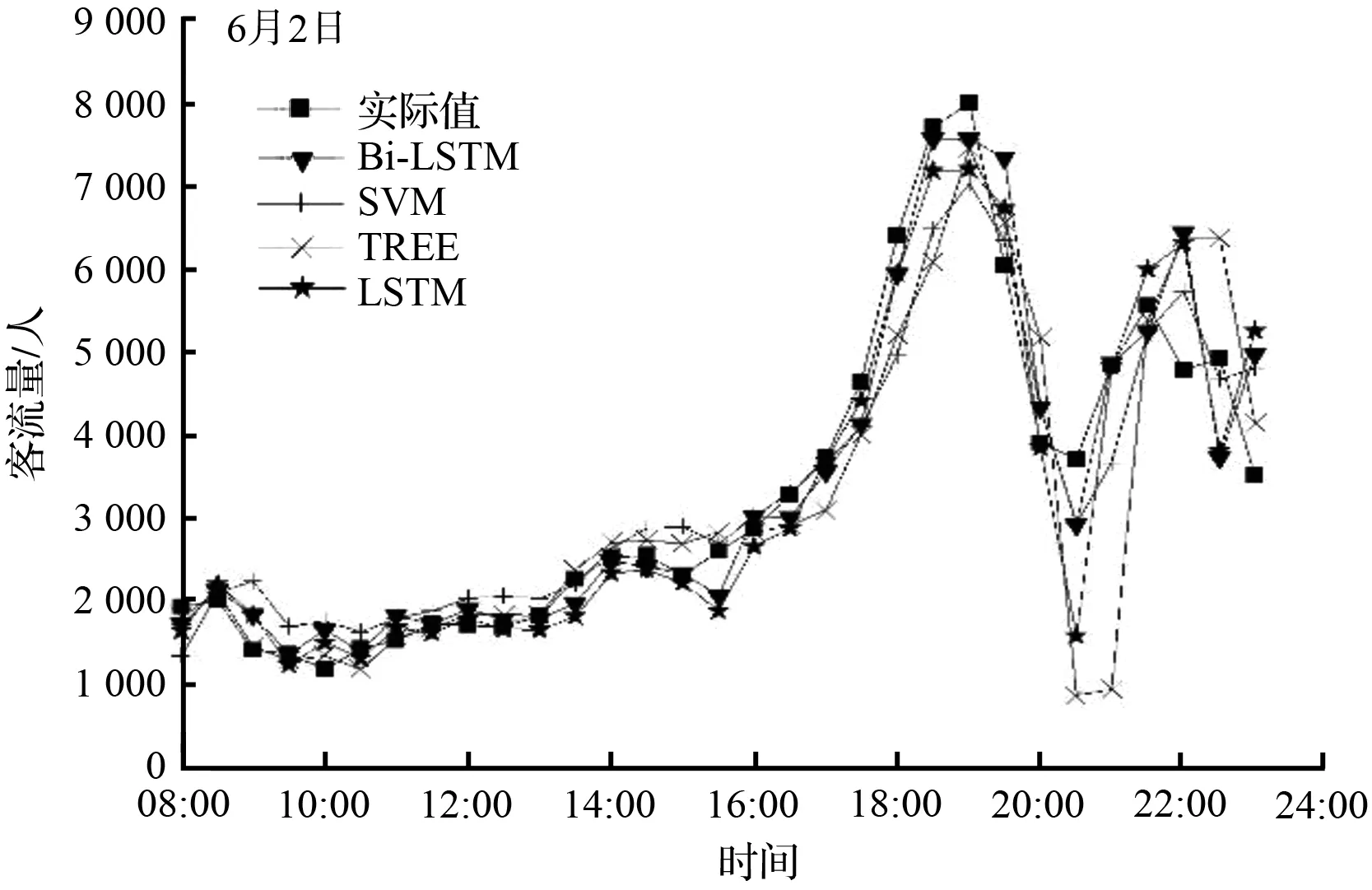
(b) 6月2日(周五)各算法预测结果比较

(c) 6月3日(周六)各算法预测结果比较

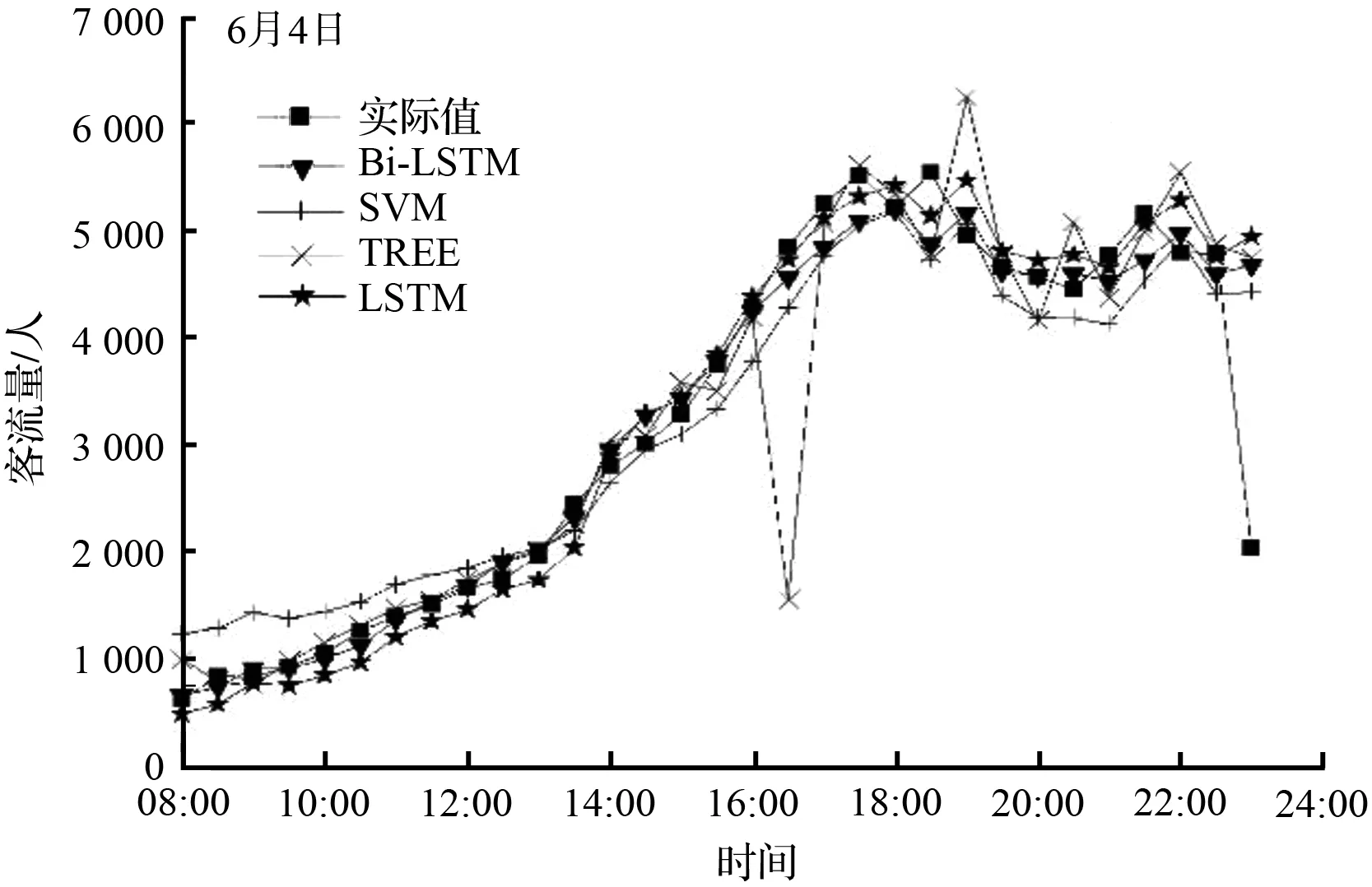
(d) 6月4日(周日)各算法预测结果比较

图9 预测结果比较
Fig.9 Comparison of prediction results

从表1可以知道，Bi-LSTM、SVM算法、决策树模型、LSTM的均方根误差(RMSE)均大于500，且决策树模型的RMSE最大，Bi-LSTM的RMSE最小。四种算法的日平均绝对百分比误差(MAPE)为9.00 %、16.58 %、13.22 %、11.56 %，误差均小于20 %。与决策树模型和SVM算法相比，深度学习算法的整体预测效果相对较好，预测精度较高，且Bi-LSTM在各项评估数据中均优于LSTM算法，日均方根误差相比LSTM降低了9.91 %，平均绝对误差百分比降低了22.15 %。同时，从表中可以看出，对6月1日～6月4日的预测，Bi-LSTM的RMSE和MAPE均小于其他算法，预测效果最好。

综上所述，在6月1日～6月4日(周四～周日)的预测中，深度学习网络总体预测效果更好，且Bi-LSTM的预测精度高于LSTM，平均预测精度高于90 %，半小时客流量的日均方根误差在500左右，预测精度较高，有较好的实用性。

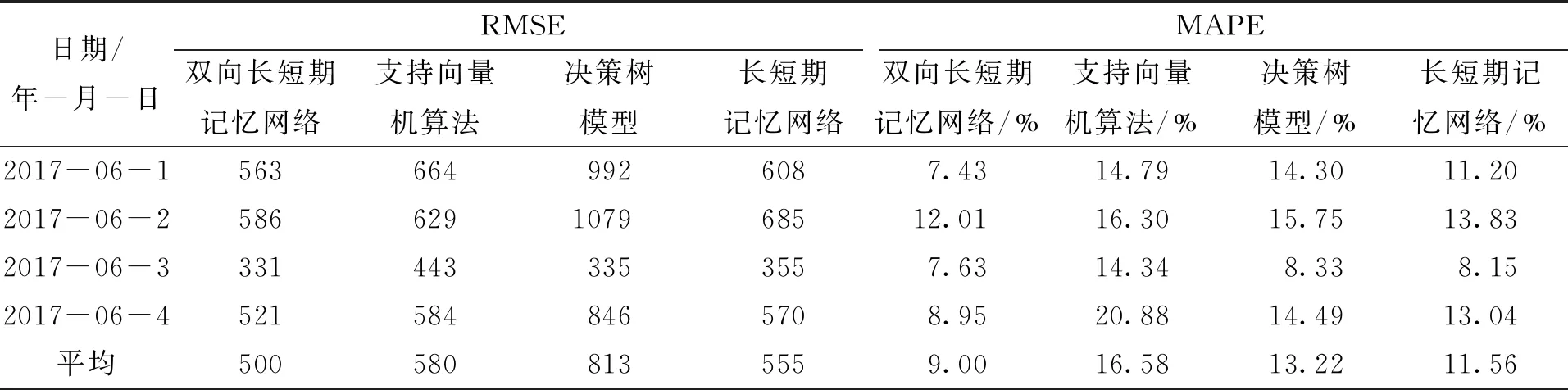
表1 评价指标对比Tab.1 Comparison of evaluation indicators

5 结语

针对地铁短时客流量难以实时准确预测的问题，本文建立了基于Bi-LSTM的地铁短时客流量的预测模型。基于广州市体育西路地铁站的进站客流量数据，进行了实证分析，得到以下主要的结论：

① 不同日期的地铁进站客流量具有一定的规律，可以根据星期主要分为周一至周四、周五及周末三类。其中，根据节假日的性质，可将节假日与周末归为同一类，节假日前一天与周五归为同一类。

② 通过对2017年5月的广州体育西路站地铁进站客流量进行Bi-LSTM模型预测，并且与决策树模型、支持向量机算法及LSTM算法进行预测结果对比，结果表明，Bi-LSTM的平均预测精度高于90 %，且优于其他算法，对地铁进站客流量预测较为准确，模型适合用于进站客流量的预测。