多规格板材电机圆片下料算法研究
陈燕*,2,龚俊舟,王婷婷,张立
(1.广西大学计算机与电子信息学院, 广西南宁530004;2.华南理工大学工商管理学院, 广东广州510640)
0 引言
在电机制造过程中,需要将硅钢片切割成圆片用于加工成定子和转子[1]。圆片下料问题是在满足圆片需求的同时最小化废料的产生,不仅可降低企业生产成本,而且对环境保护和资源节约有重要意义。
电机制造行业的圆片下料采用两阶段下料工艺,第一阶段是剪切操作,使用板材滚剪或平剪切成条带;第二阶段为冲裁阶段,即用冲床从条带上冲出圆片。针对圆片下料问题的研究已有多种算法:文献[2]采用动态规划算法和隐式枚举法生成最优的四块排样方式;文献[3]采用动态规划算法和基于列生成的线性规划生成下料方案;文献[4]采用顺序启发式算法对圆片下料问题进行求解;文献[5]在基于顺序启发式的基础上引入了分组思想求解圆片下料问题。文献[6]采用自适应遗传算法和模拟退火算法结合求解板材上的圆片下料问题。文献[7]采用基于橡皮筋势能下降策略的排样算法求解圆形钣金制品下料问题。上述文献大多是将板材切割成矩形条带,此外还可以将板材切割成平行四边形条带。文献[8]提出梯形和平行四边形条带组合的方式来求解圆片下料问题。文献[9]考虑了生成余料的下料问题,但只是针对单次订单的下料方案进行研究,没有考虑余料库存的约束。
本文针对圆片下料问题,以符合工厂实际生产的单向直切下料工艺,运用递推思想,结合顺序价值修正方法,提出一种考虑余料利用的多规格板材电机圆片下料算法,考虑连续多周期订单生产过程中余料库存控制对多种类型板材利用率的影响,利用余料作为库存缓冲,提高板材利用率。实验结果表明,允许主动生成余料策略与不允许生成余料策略相比、利用多种规格板材与利用单种规格板材相比,材料利用率都有明显提高;应用主动生成余料与不主动生成余料的策略相比,板材利用率也有明显提高。
1 数学模型
1.1 问题描述与建模
在一般的生产情况中,电机生产厂会进货多种规格的硅钢板材。在满足订单所需圆片的基础上,尽可能地提高材料利用率。设进货的硅钢板材种类数为N,Ln和Wn为第n种板材的长度和宽度,其中n=1,…,N。常规的生产过程中,一段生产时间内产出的圆片种类是重复的,设为M种(10~15种)。设订单需求的圆片种类数为m(m
本文针对上述问题的下料策略为:因使用余料条带可直接冲出标准直径的圆片,不需要进行纵剪操作,所以当前生产的订单优先使用余料条带;允许主动生成余料条带,新生成的余料条带加入余料库存供后续订单使用,充分发挥余料库存的缓冲作用。余料库存中,余料条带的种类数不能超过长期需求的圆片种类数,即小于M种。设分类库存上限约束σ限制每一种余料条带的数量,设总库存上限约束Ψ限制余料条带的总数量。
将期初作为当前下料活动的开始,开始时的余料库存称为期初余料库存,设bi为圆片的期初需求,li(li
根据上述问题为期初剩余需求li求解的下料方案数学模型为:
(1)
(2)
(3)
(4)
σk≤σ,k=1,2,…,M,
(5)
(6)
上述数学模型中,J是排样图集合,Sj是第j种排样图的余料条带面积,xj是第j种排样图的使用频率,α(j)=n表示第j种排样图是由第n种板材生成的。式(1)的优化目标为最小化板材消耗总面积,其值等于消耗整板板材的总面积与余料面积之差;式(2)约束产出的圆片数量大于或等于期初剩余需求量li;式(3)约束排样图的使用频率小于使用的板材数量;式(4)表示所有余料条带数量之和小于或等于余料总库存Ψ;式(5)约束每种新入库的余料数量小于其分类库存上限σ;式(6)表示排样图的使用次数必须为整数。
1.2 相关概念
① 条带及圆片布局:一根或多根水平条带组成板材,每根条带包含一排或多排大小相同的圆片,圆片在条带中的布局最多为3排,图1是单排条带,图2是双排条带。令圆片的直径为di,圆片到边界的最小距离为δ/2,相邻圆片间的距离为δ,其中δ称作工艺余量,圆片多于1排时,上下两排的圆心相连构成一个等边三角形。第i种g排圆片条带宽度为wig=「(di+δ)(1+(g-1)sin60°)⎤。
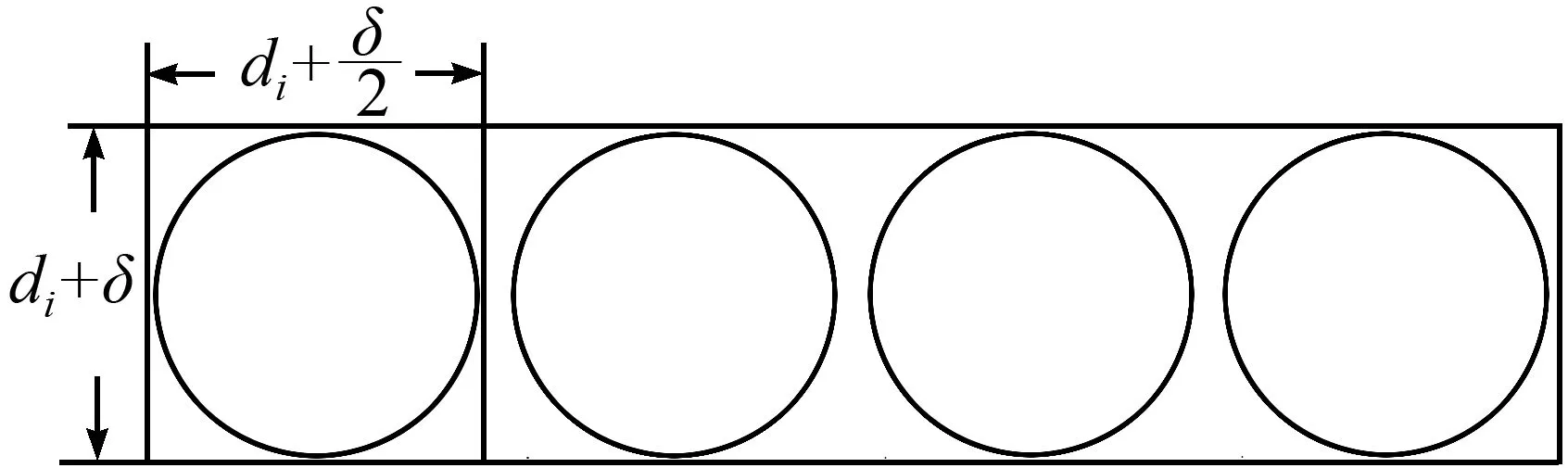
图1 单排条带Fig.1 One-row strip
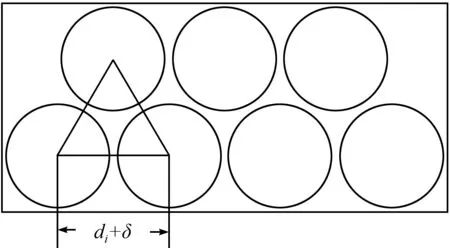
图2 双排条带Fig.2 Two-row strip
② 余料条带:每根余料条带包含的圆片是前述M种常生产的圆片之一,此种类型的圆片不在当前订单的需求中。同一种余料条带可以有不同的宽度,因为其中包含的不同排数。其中,在当前订单中产生的余料条带称为新余料条带,其入库供后续订单使用,并不在当前下料方案中使用。在过去的订单中产生的余料条带称为旧余料,该条带可用于满足当前订单及后续订单的下料需求。
③ 排样方式和排样方案:圆片在板材上的排列布局称为“排样方式”或“布局图”,一种排样方式就是具体下料时的“切割图样”。给订单需求的所有圆片确定在板材上的切割下料方案就称为“排样方案或下料方案”。一个下料方案包含一种或多种具体的排样方式及其使用频率。
2 算法设计与实现
算法涉及的部分参数如下:
G:当前迭代次数,表示当前在生成第G个下料方案。
Gmax:最大迭代次数。
vi:第i种圆片的单价,i=1,2,…,m。
σk:第k种余料条带的当前库存根数,0≤σk<σ,k=1,2,…,M。
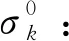
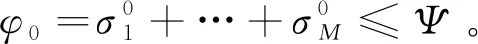
fn:第n种板材排样图的使用次数,n=1,2,…,N。
Zbest:当前最好下料方案的总成本。
2.1 排样图生成函数GetPattern()
通过枚举所有可能的条带,在板材的长边布局一根余料,以使布局图的产出率达到最大。生成排样图的数学模型表示为:
(7)
(8)
(9)
(10)
上述模型为有约束的背包问题,其中vi为圆片的单价,λi为板材内有效圆片的数量,zi为当前排样图所含圆片数量,li为圆片剩余需求量,其中i=1,2,…,m;K为当前剩余需求圆片对应的所有可行条带的种类数,wt为条带宽度,χt为条带数量,其中t=1,2,…,K。式子(7)表示模型优化目标是使板材价值利用率最大化,即板材包含有效圆片的总价值最大;式子(8)表示当前排样图所含第i种圆片数量等于所有条带所包含的同种圆片数量;式子(9)表示第i种圆片的有效个数是剩余需求li与实际布局的圆片个数zi两者中的较小值;式子(10)约束排样图中条带组合后的总宽度不大于板材的宽度。
图3是一个包含余料的排样图,其中有2条当前订单需求条带和1条余料条带。

图3 一个包含余料的排样图Fig.3 A cutting pattern with leftover
具体的求解过程如下所述:
step 1:令n=0,最优布局图的产出率Obest初始化为零,即Obest=0。
step 2:若n=N,转step 6;否则令n=n+1,转step 3。
step 3:若qn=0,转step 2;否则求当前剩余需求圆片的一个最优排样图,在长宽为Ln⊗Wn的板材从宽度方向上进行遍历条带拼接,每次只拼接一根条带,直到组成整张板材上的排样图Pn,此时所有拼接的条带宽度之和必须小于Wn,并记录此种不拼接余料条带的排样图产出率On。
step 4:遍历库存中所有的余料条带,在当前规格板材上从宽度方向上进行遍历余料条带拼接,每只拼接一根余料条带,记录其中最大产出率O0n和其排样图P0n,并记录用来拼接的余料条带。
step 5:将当前最大产出率Obest、无余料条带排样图的产出率On和有余料条带排样图的产出率O0n三者进行比较,把其中最大者记为当前最大产出率Obest,并把Obest对应的排样图记为当前最好排样图Pbest。令n=n+1,转step 2。
step 6:输出当前最大产出率Obest和最优排样图Pbest。
在确定最优排样图后,排样图的使用频率确认分为两种情况:
① 最优排样图中没有产生余料条带,根据式(11)确定最优排样图的使用频率。
② 最优排样图中含第k种余料,根据式(12)确定最优排样图的使用频率。
(11)
(12)
2.2 圆片价值修正函数CorrectValue()
单一的顺序法求解下料方案的过程中不改变圆片的价值,只会产生单一的下料方案。为了得到利用率更高的排样方案,在生成当前排样方式之后,需要根据剩余圆片种类和需求量调整圆片的价值,使之生成多种不同的排样方式。本文采用的圆片价值修正公式如下:
(13)
(14)
(15)
其中Ω和p均为控制参数,u为当前布局图的板材利用率,si为第i种圆片的单片面积,p=1.03,Ω=0.75。
2.3 下料方案生成算法
允许在板材上布局一根水平方向的余料(图3),下料方案生成算法步骤如下:
Step 1:令G=0;初始化vi为圆片面积,其中i=1,2,…,m;初始化最好下料方案总成本Zbest=+∞。
Step 2:若G=Gmax,转step 9;否则G=G+1。
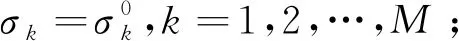
Step 4:调用GetPattern()函数生成排样图Pbest,记录该排样图使用频率fn,n=1,2,…,N。
Step 5:将排样图Pbest加入当前下料方案,更新圆片剩余需求量li=li-fnyi,i=1,2,…,m。更新第n种板材的数量qn=qn-fn。若当前排样图中含有第k种余料条带,则令余料的当前分库存σk=σk+fn,当前总库存φ=φ+fn。
Step 6:调用CorrectValue()函数修正圆片价值。
Step 7:如果存在li>0,其中i=1,2,…,m,即圆片需求量还未满足,转step 4。
Step 8:若当前下料方案总成本小于最好下料方案总成本,即Z
Step 9:输出最好的下料方案。
3 实验
本文算法基于C#语言实现,电脑配置为CPU Intel(R) CoreTMi7-5500U 2.4 GHz,RAM 8 GB,程序在操作系统WIN10上执行。根据电机行业实际生产情况,对某电机厂实际生产中的30个连续订单(订单数据详见附表1),分别应用有余料策略和无余料策略,分析几种不同板材使用时消耗面积和节材率的不同。其中:
有余料策略:在排样过程中允许主动生成规范余料条带;
无余料策略:在排样过程中不允许主动产生余料条带。
3.1 单板材实验数据分析
分别使用3种不同尺寸的标准板材2 000×1 000、2 500×1 000和2 000×1 500,应用上述两种策略给30个连续订单确定下料方案,消耗的板材面积和节材率如表1所示。

表1 单种板材组合的节材率Tab.1 Cost saving rate of one types of sheet
tN和LT分别表示两种策略为每个订单求解下料方案所需要的平均运行时间。SN和SL分别表示应用两种策略所消耗的板材总面积。ΔS表示应用有余料策略对无余料策略的节材率,其值为ΔS=[(SN-SL)/SN]×100 %。UN和UL分别表示应用两种策略30个订单的总体利用率。ΔU表示无余料两种策略的利用率的差值,其值为ΔU=UL-UN。
从表1可看出,同一订单下使用三种不同规格板材的节材效果不同,最低的是第三种板材,差不多达到了2 %,最高是第二种板材,达到5 %以上,三种板材的节材率平均达到3.24 %。在以上三种板材计算30个订单的平均时间分别是2.90、3.36、2.78 s,都在较短时间内完成。因此,对采购板材种类数的建议为,按照实际订单情况对所有规格板材进行下料预计算,根据计算结果指导采购选择。
3.2 双板材实验数据分析
将上述三种板材进行两两组合,分析两种板材组合的节材率。分别应用有余料和无余料两种策略给上述的例题下料,消耗的板材面积和节材率如表2所示。从表2中可知,不同尺寸的板材组合供同一订单下料,节材率的差别不如单板材的大。两两组合的平均节均率为2.54 %,比单板材的平均节材率3.24 %稍低,原因是其中两种板材的利用率较低。

表2 两种板材组合的节材率Tab.2 Cost saving rate of two types of sheets
3.3 三种板材实验数据分析
针对上述实验订单,分别应用有余料条带策略和无余料条带策略,使用三种板材同时进行优化组合下料,消耗的板材面积和节材率见表3。从表3中可知,仅有两种板材供下料的节材率2.54 %,略高于三种板材同时供下料选择时的节材率2.35 %,原因是其中两种板材组合的利用率较低。

表3 三种板材组合的节材率Tab.3 Cost saving rate of three types of sheets
在多规格板材可供下料时,不同板材下料方案的平均消耗成本如表4所示。其中板材种类1代表单板材、种类2代表两种板材、种类3代表三种板材。S总表示板材消耗总面积,ΔS总表示不同板材种类数所消耗的板材面积的差值。例如第二行第二列的ΔS总值等于S总列中第二行减去第一行的差值,即26 285.0-27 510.9=1 225.9。因此第一行的ΔS总为空值,用“-”表示。U表示不同板材组合使用时,企业长期下料使用板材的利用率,ΔU表示不同种类板材利用率的差值。ΔU的计算方法与ΔS总计算方法类似,第二行的ΔU值等于U的第二行的值减去第一行的值。

表4 三种组合方式的平均消耗成本Tab.4 Average consumption cost of three combination mode
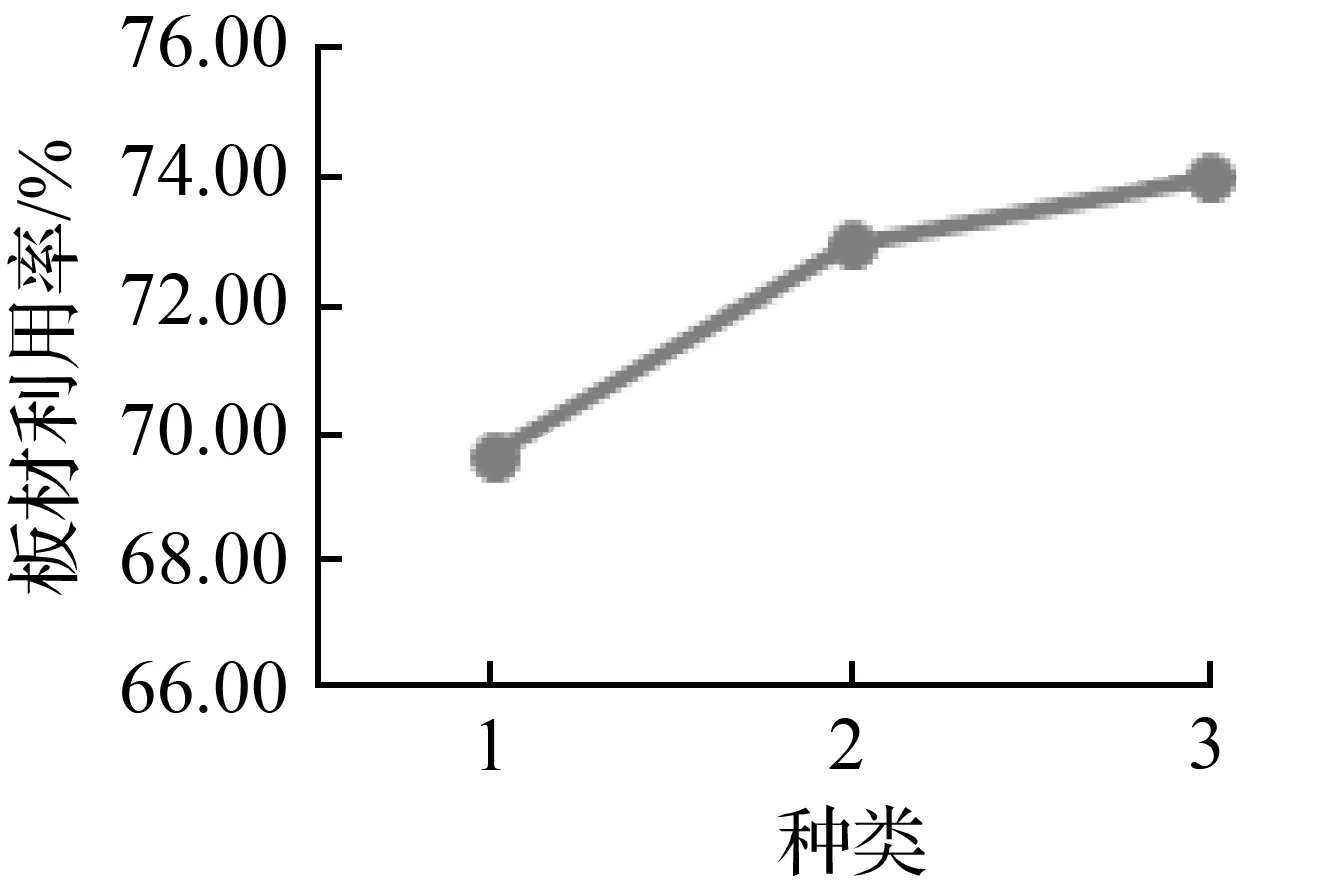
图4 板材利用率和板材种类数的关系Fig.4 Relations between utilization and species number of sheets
从表4可知,随着可供下料使用的板材种类数增多,板材利用率在逐步提高。只有一种板材供选择时,利用率不到70 %;三种板材可供下料时,利用率差不多达到了74 %,比只有一种板材时提高约4 %。
根据上述三个表的数据绘制了图4,从图4可知,随着板材种类数的增多,板材利用率的提升速度是变慢的。但板材利用率变化与板材种类数的关系并不是直线上升、而是呈折线上升状态,其斜率逐渐渐变小、板材利用率上升趋势变慢。因此,在条件允许时建议企业可定购多种规格板材,但不需要太多,通常在3种左右,板材利用率就会有明显的提升。
4 结论
本文针对圆片的单向直切下料问题,提出多规格板材的顺序优化排样算法,主动考虑余料的生成,并控制余料产生的数量缓冲库存。在保证直切下料工艺简单性的前提下,应用本文算法可使长期生产的材料利用率得到较为明显的提高。利用余料的控制策略,可供电机生产厂及不锈钢制品业参考。

