一种基于MeanShift改进的移动目标跟踪算法*
邹梓秀
(福州理工学院 福州福建 350202)
关键字: MeanShift算法,移动目标跟踪,车联网
移动目标的跟踪是当前车联网研究热点,MeanShift算法是业界非常著名的跟踪算法,是Fukunage学者在1975年提出的[1]。谢达奇等学者把MeanShift算法应用到焊点检测中,利用最小二拟合与MeanShift算法相结合完成若干圆心点的收集,通过实验对比验证了该方法的有效性[2];周正钦等学者扩展了均值漂移聚类,引入了邻域权重因子,实现了红外图像中热故障区域的有效提取,取得了很好的效果[3];李旺灵等学者对Meanshift算法提出了锥套跟踪的自适应核窗口思想,提高了算法的适应能[4];孟一飞等学者利用MeanShift算法来识别西夏文字笔形,这是一个很新颖的思路,利用核估计直方图统计方法,提取西夏文字的特征值,实现智能识别[5];朱闻亚等学者对Meanshift算法进行了改进,引入了稳健估计,部分实现了跟踪丢失问题,但当跟踪目标快速通过时仍然可能导致跟踪目标丢失[6];成怡等学者利用Meanshift算法与摄像机标定相结合,实现了无人机定位问题[7]。很多学者对Meanshift算法进行了深入研究,在诸多领域都有很多应用;也有很多学者对该算法进行了多个角度的改进,但跟踪目标在快速行进时容易丢失、跟踪目标中途改变形状等问题仍然不够理想,文章把MeanShift算法应用到车联网中,并针对其缺陷进行改进。
1 MeanShift算法
Meanshift算法的主要目标是计算当前坐标点与移动目标的偏移向量的均值,然后移动到该点,并以此为新的起点,不断迭代该过程,直到满足条件为止,如图1所示(图来自https://my.oschina.net/u/3702502/blog/1815341)。
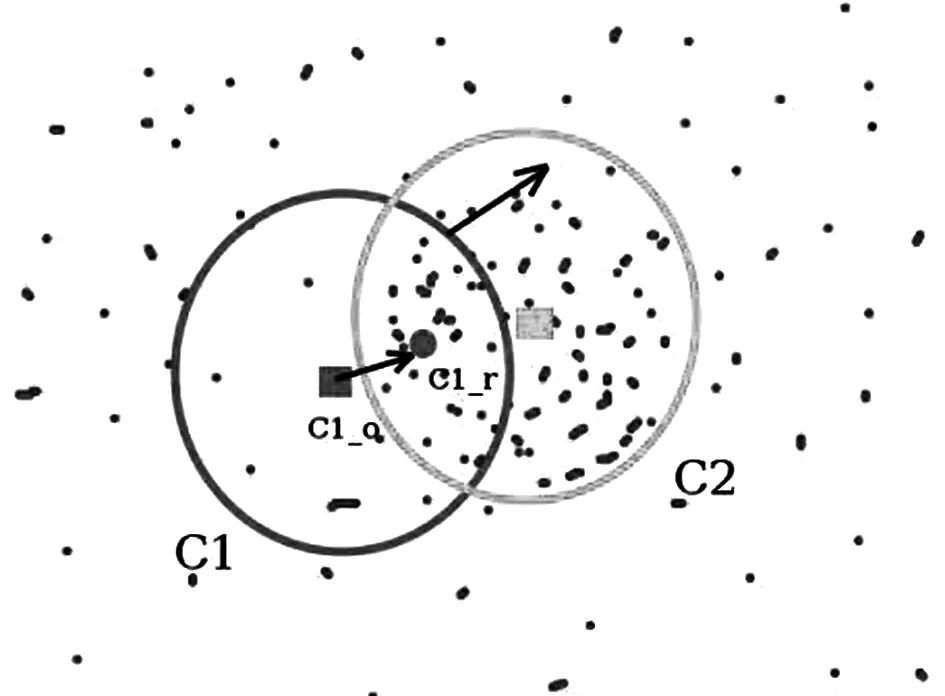
图1 向量均值
图1中C1_O表示目标的起始点,C1、C2为监视框,当目标移动到C1_r时,计算两点之间的偏移向量的均值,并向做移动,然后不断迭代直到C1与C2重合为止,具体实现步骤如下:
(1)偏移向量均值计算。某高维度区域,设其半径为r,该区域有n个目标对象,计算某D点与其它点Di偏移向量均值,其公式为:
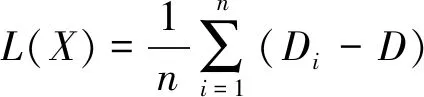
(1)
(2)核函数的引入,为了更快地移动到目标位置,绝大部分的目标跟踪都会引入核函数,把MeanShift算法转化为基于密度的聚类算法。高斯核函数是最常用的密度函数,设高维空间中任意两点x1、x2的距离记作k(|x1-x2|),高斯核函数的计算公式为:

(2)
通过高斯核函数的转换,MeanShift算法的偏移向量均值的计算公式变为:
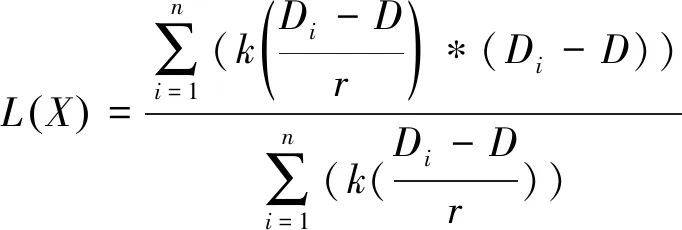
(3)
通过高斯核函数的变换,从式(3)可以看出目标将向概率密度上升的区域移动,从而实现目标的跟踪。
2 MeanShift算法改进
MeanShift算法是一种很成熟的跟踪算法,在实践中得到了广泛应用,但适应能力有待提高,例如移动目标大小发生变化时,由于MeanShift算法的跟踪框是固定的,容易导致丢失跟踪目标。此外,由于车联网中,车辆运行一般比较快,这需要算法反应比较灵敏,但MeanShift算法由于纬度高、计算量大,也可能导致丢失跟踪目标。针对这两个缺陷,可从以下几个方面进行改进:
(1)跟踪框的改进。如图1的C1框是固定的,如果跟踪过程中正好下雨,某移动目标撑起了雨伞,那么跟踪目标的大小发生了很大的变化,为了不会丢失移动目标,文章增加一个实时形态监测函数,用于在计算偏移量均值时同时计算移动目标的大小,实现过程:首先获得移动目标的坐标(x,y)和宽高w、h,然后根据坐标和宽高构造矩形框,返回矩形框Rec(x,y,w,h)。
(2)核函数改进。文章使用的是高斯核函数,该函数有一个参数半径r,该参数是固定的,单位频率采集时间内,目标移动速度越大,根据式(2)可知得到的结果越小,因此文章通过增设一个权重来调整半径的值,以弱化该趋势,从而避免由于速度较快导致跟踪目标丢失问题,把式(2)进行改造,得:
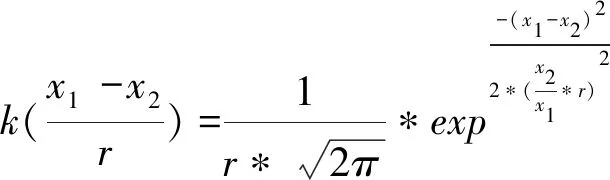
(4)
从式(4)可以看出,改进后的公式在指数的分母增加了x2/x1的比例权重来削弱移动趋势,即移动速度越快,x2/x1的比例越大,则式(4)得到的值比式(2)的值更小,因此式(3)需要迭代的次数也就减少了,从而减少了计算量,增强了整个算法反映速度,即反映会更灵敏,改进后的算法命名为E-MeanShift。
3 仿真实验
在福州大学城某高校的校园主干道中安排了一场实验,主干道长度3.3km,双向两车道,实验安排在某星期六完成。第一组实验,安排10人步行(正常速度),3人骑电动车(大约20km/h),行进中途,随机安排步行中的3人打开雨伞,并继续前行。

图2 跟踪能力对比图
图2的实验结果表明,MeanShift算法跟踪成功率为100×10/13=76.9%,目标丢失率为100×3/13=23.1%;E-MeanShift算法的成功率为100%。通过后台的监控知道MeanShift算法丢失了三个中途打雨伞的目标,说明该算法对中途目标大小的变化无法适应,而E-MeanShift算法增加了实时监测函数,不受此影响。
第二组实验,安排3辆电动车(大约40km/h),3辆汽车(大约60km/h)参与实验,当电动车和汽车陆续通过时,发现MeanShift算法和E-MeanShift算法都能全部跟踪到,原因在于电动车和汽车行进中都不会改变尺寸大小,并且速度较慢。
第三组实验,为了检验跟踪效果,实验场地安排在某练车场,经与私营业主的许可,获得了4.5km两车道场地1h的使用时间,3辆汽车以100km/h的速度通过,实验结果:MeanShift算法2辆汽车跟踪成功,其中1辆跟踪目标丢失,并且系统感受到明显的“卡顿”,即跟踪不够流畅;E-MeanShift算法3辆全部跟踪成功,实验证明在高速通过时E-MeanShift算法的跟踪能力较出色。由于实验场地有限,科研经费有限等原因,文章未检验超过100km/h的速度,也未检测更多车辆同时通过的情况,但从该实验可以预计更高速和更多车辆的情况下,E-MeanShift算法的优势会更明显。
4 结语
文章为了解决车联网中移动目标跟踪问题,利用MeanShift算法和高斯核函数来跟踪移动目标。由于MeanShift算法存在诸多缺陷,文章提出了两个方面的改进,通过3组实验证明改进后的算法在适应能力方面和移动目标高速通过时具有一定的优势。

