碳酸盐岩酸蚀蚓孔等效渗透率影响因素研究
严伟丽,许崇祯,陈 坤
(1. 长江大学 地球物理与石油资源学院,湖北 武汉 430100; 2. 中石化销售股份有限公司江苏石油分公司,江苏 南京 210000)
随着碳酸盐岩储层的持续开采与生产,工程所用的流体以及地层中的微粒会使得近井筒地带的储层受到污染,从而导致渗透率下降,因此需要引入增产措施来改善地层渗透性[1]。基质酸化通过在近井筒区域制造有高导流能力的通道来实现有效增产,该通道就是“酸蚀蚓孔”,使得油井周围地层渗透率提高,进而提高产能。而酸蚀蚓孔的生长对酸化的效果有着较大的影响[2],因此对酸蚀蚓孔的形态特征以及渗透率的研究就显得尤为必要。
水平井酸化蚓孔形态的模拟,运用“点到圆”二分叉树状分形网络渗流模型,分析了不同蚓孔参数对蚓孔区无量纲等效渗透率的影响,以及推导了考虑各蚓孔半径不等情况下的分形分叉网络渗透率计算模型,分析了流动最优化状态下,不同参数对蚓孔酸化区等效渗透率的影响。
1 二分叉分形树状分叉网络
常见的树状分叉网络,例如植物躯干网络、三角洲的河道网络、裂缝网络、地下储层的孔隙渗流网络等等,这些树状分叉网络系统具有很好的自相似性,这为分形几何理论的运用提供了很好的依据,也说明了类分型树叉网络通过分形几何理论解释的可能性[3]。
类分形树状分叉网络渗流比较复杂,要想利用分形理论处理首先必须对其进行简化。简化的思路是将分叉网络从最简单的一级分叉开始寻找规律,建立每一级之间的联系,然后通过迭代一步步计算到各级,从而形成一个系统的分叉网络。迭代规则简单来说,首先由一根圆形毛细管作为母管,然后在分叉角给定的情况下进行分叉,分出两个或者两个以上的子管,依次类推,每个子管也分出相同数目的子管,不断重复直至完成[4]。
首先来对单分叉结构进行分析,图1是第k级单分叉示意图。为了简化计算[5],每一级的分叉管道可以假设为横截面为圆形的直管,并且忽略掉管壁。以第k级分叉结构而言,rk和lk分别表示第k(k=0,1,2,…,m)级分叉管道的半径和长度,用rk+1和lk+1分别表示第k+1级分叉管道的半径和长度,分叉角为θ,分叉级数为m,分叉数为n,对于二分叉网络来说n=2,k级分叉管道的总数为Nk,网络所有的分叉管道数为N。我们先定义两个系数,分别将αk作为相邻两级分叉管道的长度比,βk作为相邻两级分叉管道的半径比,其数学表达式为:
αk=lk+1/lk
βk=rk+1/rk
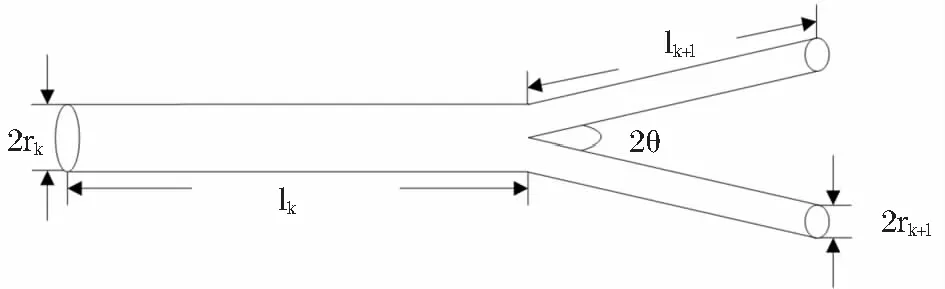
图1 第k级单分叉结构示意
对于平面分叉网络系统而言,分形维数一般在1~2之间,分形维数越大,其所构成的分叉网络系统覆盖的面积也越大,对于二分叉网络,α、β的取值范围在0.5~0.7之间。
2 等效渗透率影响因素分析
分别讨论二分叉网络长度分布分形维数Dl、半径分布分形维数Dr、分叉级数m以及分叉角θ对二分叉网络等效渗透率的影响。
为了研究分叉级数级数与无量纲等效渗透率的关系,假设初始蚓孔长度l0=0.3,二分叉网络分叉角θ=30(°),二分叉网络长度分布分形维数Dl=1.8,二分叉网络半径分布分形维数Dr=1.6,通过VB程序绘制分叉级数与无量纲等效渗透率的关系曲线,见图2。

图2 不同二分叉长度分形维数下分叉级数与无量纲等效渗透率的关系
从图2可以看出:在其他参数给定的情况下,二分叉网络的无量纲等效渗透率随着分叉级数的增加而降低。这是因为随着分叉级数的增加,分叉级数m越大,分叉管道最后一级的管半径就越小,整个二分叉网络系统的渗流阻力迅速增加,使得无量纲等效渗透率快速下降。
紧接着改变二分叉网络长度分布分形维数,分别绘制Dl=1.2、1.5、1.8时,无量纲等效渗透率与分叉级数的关系曲线,见图2。在观察同一分叉级数时的Dl,可以发现:①不同二分叉长度分布分形维数Dl下,无量纲等效渗透率都随分叉级数的增加呈下降趋势;②随着二分叉网络长度分布分形维数Dl的增大,无量纲等效渗透率逐渐减小。通过理论可知,相同分叉级数下随着Dl的增大,长度分叉比增大,各级流体流过的长度增加,流动压降增大,渗流阻力增大,从而使得无量纲等效渗透率减小。
同理,改变二分叉网络半径分布分形维数,分别绘制Dr=1.2、1.5、1.6时,无量纲等效渗透率与分叉级数的关系曲线,见图3。

图3 不同二分叉半径分形维数下分叉级数与无量纲等效渗透率的关系
如图3观察同一分叉级数时的Dr,可以发现:①不同二分叉半径分布分形维数Dr下,无量纲等效渗透率都随分叉级数的增加呈下降趋势;②随着二分叉网络半径分布分形维数Dr的增大,无量纲等效渗透率呈现逐渐增加的趋势。通过理论可知,随着Dr的增大,半径分叉比增加,各级半径增加,使得渗流阻力减小,从而使得无量纲等效渗透率增加。
同样,研究分叉角与无量纲等效渗透率的关系,通过VB编制分叉角与无量纲等效渗透率的关系曲线,如图4所示。
通过图4我们可以看出:随着分叉角的增大,无量纲等效渗透率呈现下降趋势,这说明分叉角的增大使得二分叉网络管道的迂曲度增大,增大了渗流阻力,进而使得等效渗透率降低。

图4 分叉角与无量纲等效渗透率的关系
3 结 论
通过编制的VB程序,运用二分叉网络等效渗透率模型,通过实例计算,分析了二分叉网络长度分布分形维数、二分叉网络半径分布分形维数、初始蚓孔长度以及初始蚓孔半径对蚓孔酸化区等效渗透率的影响。
1)随着分叉级数的增加,二分叉网络的无量纲等效渗透率降低。
2)随着二分叉网络长度分布分形维数的增大,无量纲等效渗透率逐渐减小。
3)随着二分叉网络半径分布分形维数的增大,无量纲等效渗透率呈现逐渐增加的趋势。

