基于PR控制及高频信号注入的双三相永磁同步电机无位置传感器控制

徐 斌，罗 响，朱 莉

(上海交通大学 电气工程系，上海 200240)

0 引 言

和传统的三相永磁同步电机相比，多相永磁同步电机具有很多优势，如较低的转矩脉动、较低的直流母线电流谐波、低压大电流以及高可靠性[1-2]。因此它被广泛应用到需要高可靠性和电压等级被电池电压限制的领域，如水下推进器、电动汽车等[3-4]。

双三相永磁同步电机是多相永磁同步电机的一种，又名不对称六相永磁同步电机，由两套相差30°电角度的三相定子绕组构成。这两套三相绕组由一台电压型六相逆变器驱动，如图1所示。图中，ABC和UVW分别为两套定子绕组。

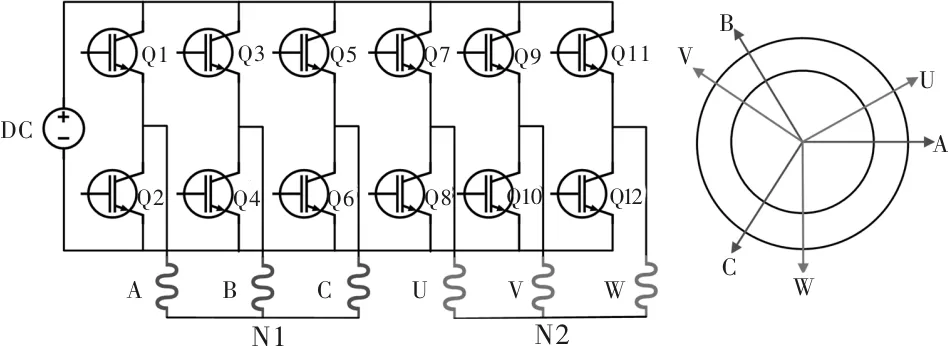
图1 双三相永磁同步电机驱动

为了得到优异的控制性能，电机的转子位置是必需的。通常是把编码器或旋转变压器连到转子转轴上来获得转子的精确位置。但是这些位置传感器有几个缺点，如低可靠性、额外的花费、体积增长等。因此在过去的二十年，电机的无位置传感器变得越来越受欢迎。

永磁同步电机的控制算法主要分成两种。一种是基于反电动势估计技术。当电机处于中高速时，这种无位置控制算法具有良好的控制性能。但是当电机处于低速甚至零速时，反电动势很小甚至为零，导致提取反电动势的信号信噪比很低，带来极差的控制性能。另一种方法是基于转子凸极性，如高频信号注入法。当电机处于零速或低速时，这种方法能很好的估测电机的转子位置。

对于双三相永磁同步电机，这些基于反电势估计或转子凸极性的无位置控制算法也是适用可行的[5]。文献[6]基于反电动势估计，设计了模型参考自适应控制系统，实现了无位置传感器控制。控制系统的稳定性由Popov超稳定理论验证。但是由于这个模型参考自适应系统是基于反电动势估计的，因此不适合低速无位置传感器控制。文献[7]提出了一种改进的零序载波脉动信号注入方法。在两组注入的高频脉振信号有一个最优的相角差来减少谐波，但是在两个三相绕组中性点之间需要一个额外的电压传感器来测量零序电压。如果只在一套三相绕组中注入高频电压信号，虽然可以实现双三相永磁同步电机的无位置传感器控制，但是注入的高频电压信号也会在另一套绕组中感应出高频电流，从而影响控制性能。因此，抑制第二套绕组中的高频电流响应就能减少谐波，降低转矩脉动，可提升无位置传感器控制的性能。

本文提出了一种基于PR(比例谐振)控制的高频信号注入双三相永磁同步电机无位置传感器控制方法。一组高频余弦电压信号被注入到ABC绕组的估测d轴。将高频电流响应通过一个带通滤波器和一个低通滤波器，可以得到转子位置估计误差。再通过锁相环可以得到估计的转子位置。同时使用PR控制器抑制UVW绕组中感应出的高频电流，以抑制高频电流导致的转矩脉动，提升控制性能。仿真结果和实验结果验证了PR控制可以有效地抑制UVW绕组中的高频电流响应，提升了双三相永磁同步电机无位置传感器控制的性能。

1 高频注入算法

根据双d-q同步坐标系理论，双三相永磁同步电机的两套三相定子绕组可以通过两个相位相差30°的Clarke-Park变换阵变换到同一个d-q坐标系上[8-9]。变换之后，电压方程为

(1)

式中,ud1、uq1为第一套绕组的d轴和q轴电压;ud2、uq2为第二套绕组的d轴和q轴电压;id1、iq1为第一套绕组的d轴和q轴电流;id2、iq2为第二套绕组的d轴和q轴电流;ω为角频率;Rs为定子绕组相电阻;ψfd为转子永磁体磁链;Ld、Lq为d轴和q轴电感;Ldd、Lqq为d轴互感和q轴互感;

使用高频信号注入进行无位置传感器控制时，只考虑高频分量[10]，因此双三相永磁同步电机的高频电压方程可化简为

(2)

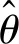
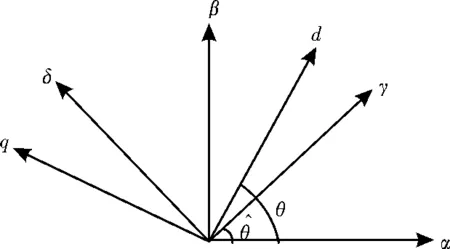
图2 双三相永磁同步电机估计坐标系

文中，一组高频余弦电压信号被注入到ABC绕组估测的d轴，即γ轴，如式(3)所示:

(3)

式中,Uh为高频电压信号的幅值，ωh为高频电压信号的频率。

在估计的d-q坐标系即γ-δ坐标系中，高频电压方程可写成

(4)

(5)

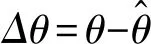
(6)

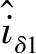
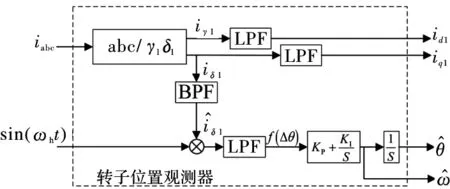
图3 转子位置观测器框图

2 PR控制

由式(6)可以看出，在ABC绕组中注入高频信号，会在UVW绕组中感应出高频电流。由于UVW绕组中的高频电流对转子位置估计没有作用，只会导致转矩脉动增加。因此，抑制UVW绕组中的高频电流，可以减小因高频电流导致的转矩脉动，提升无位置传感器控制性能。

由于注入的高频电压信号频率固定，产生的高频电流也是固定的，因此可以使用PR控制器来抑制UVW绕组中的高频电流响应[11-12]。理想PR控制器的传递函数为

(7)

式中,KP为比例增益，KR为谐振增益，ω0为谐振频率。但是这个理想PR控制器只对单一的频率ω0起作用，如图4所示。但由于测量采样的不准确性，实际上会使用以下的变形，以对一定范围的频率起作用。

(8)

式中,ωb为谐振带宽。这个PR控制器称为准PR控制器，实际运用中，PR控制器一般就指准PR控制器。理想的PR控制器和准PR控制器的Bode图如图4所示，以KP=1，KR=100，ωb=3rad/s，ω0=500*2πrad/s为例。

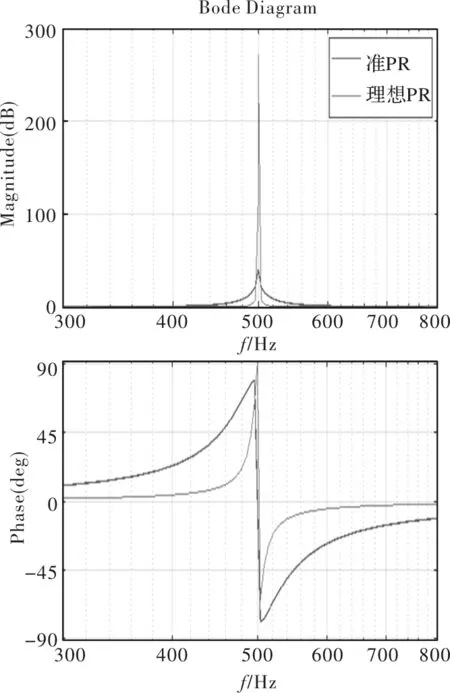
图4 PR控制器Bode图

根据电机的参数，需要对PR的参数进行整定。由于PR控制只在UVW中使用，因此以UVW绕组id2的控制为例。由于积分环节主要作用是消除静差，因此主要是整定KP、KR。系统的控制模型如图5所示。

图5 UVW绕组id2控制模型

式中,uh为注入的高频信号产生的扰动，T为控制周期，Udc为直流母线电压。

首先对KP进行整定，忽略谐振环节和扰动环节，系统的传递函数为

(9)

特征方程为

(10)

阻尼比为

(11)

KP=0.125

(12)

此时，对于扰动回路，若没有谐振环节，阻抗大小为

ZP=sLd+KPe-sTUdc

(13)

将s=jωh代入，其中ωh=500*2πrad/s为注入高频信号的角频率，可得扰动回路阻抗为

ZP=8.03∠18.59°

(14)

由式(14)可知，扰动回路阻抗小，对高频信号抗扰能力差，需要加入谐振环节，取ω0=ωh=500*2πrad/s，ωb=3rad/s此时扰动回路阻抗为

(15)

要使由高频扰动uh产生的电流抑制为原来的3%，则需使ZPR是ZP的33.3倍。取KR=5，有

(16)

达到了电流抑制的目标，此时整个控制系统的Bode图6所示。由图6可以看出，加入谐振环节后，系统相位裕度为46.6°，PR控制能够保持稳定。

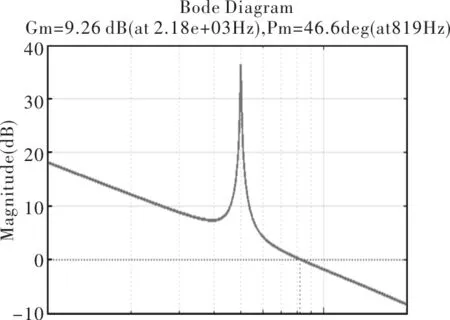
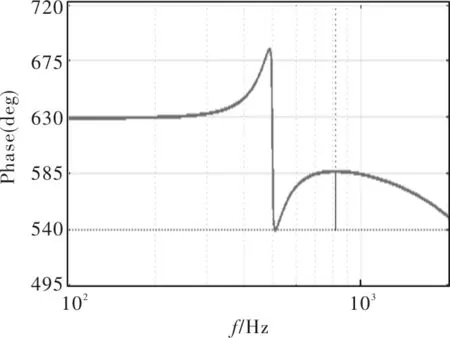
图6 PR控制系统Bode图

3 仿真及分析

具体到控制，两套三相绕组各自由经典磁场定向控制系统控制。此时

(17)

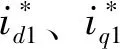
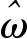
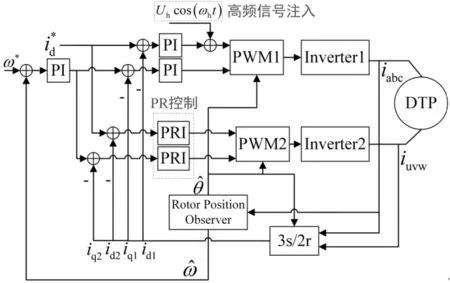
图7 基于PR控制的单绕组高频信号注入控制框图

根据PR控制的单绕组高频信号注入控制框图以及PR控制器参数，在Matlab/Simulink中建立相应的仿真模型，电机的参数如表1所示。

表1 电机参数

给定转速设为120r/min，直流母线电压设置为64V。ABC绕组注入的高频信号为fh=500Hz,Uh=3.2V。在无PR控制时，A相电流、U相电流以及U相电流FFT如图8所示。

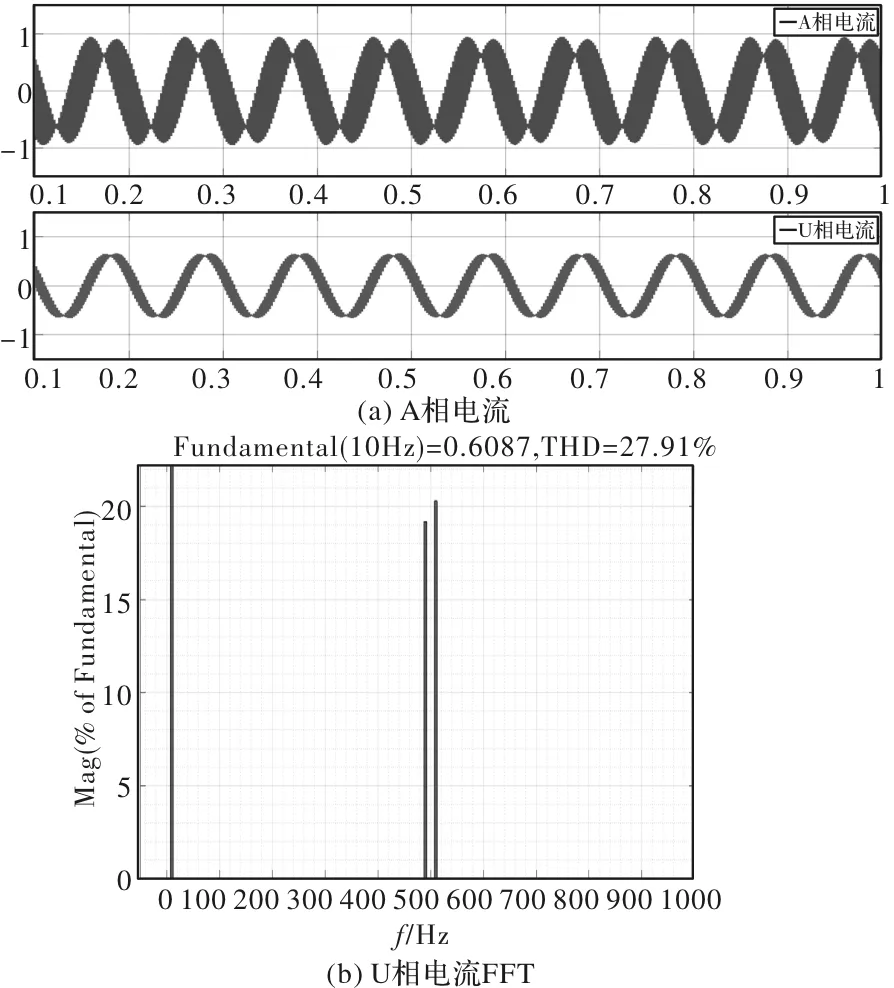
图8 无PR控制

由图8可以看出，在没有使用PR控制时，U相电流含有较大的500Hz高频感应电流，THD有27.91%。由于叠加了电流角频率，因此相电流中高频电流频率不是正好500Hz。

加入PR控制后，A相电流、U相电流以及U相电流FFT如图9所示。

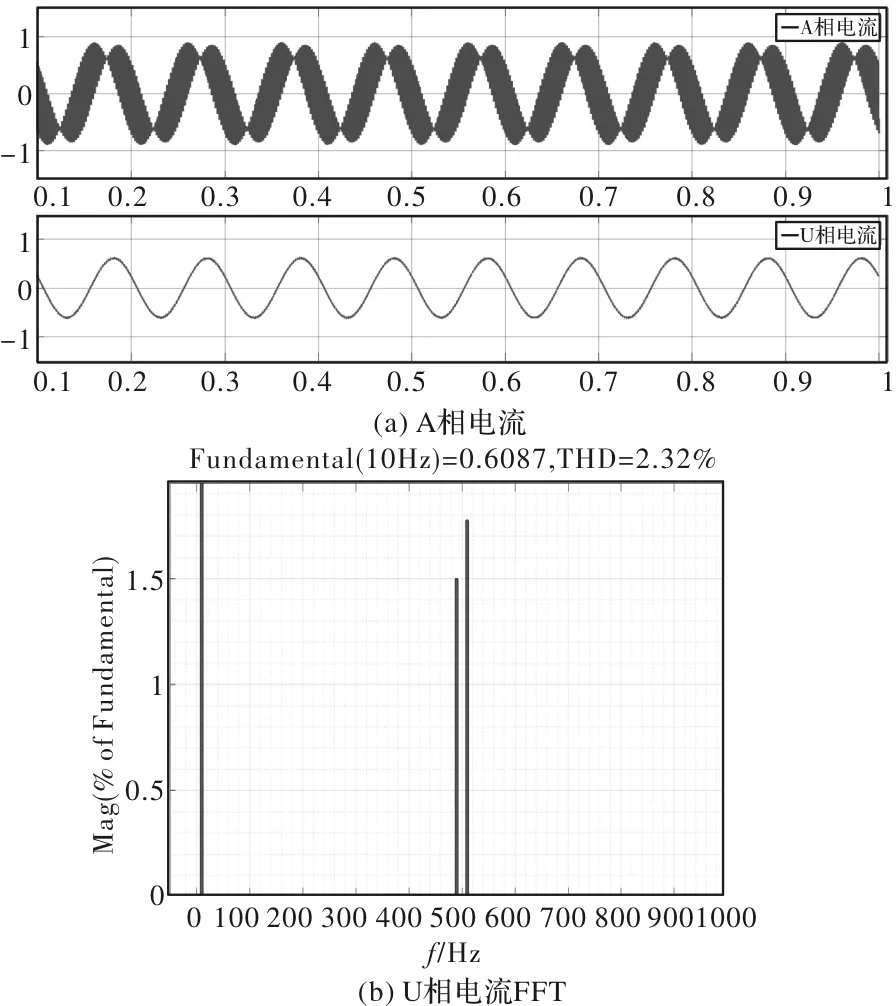
图9 有PR控制

由图9可以看出，在使用PR控制后，U相电流中的500Hz高频感应电流很小，THD只有2.32%，说明PR控制可以完美地抑制UVW绕组中的高频感应电流。

4 实验结果及分析

根据控制理论和仿真模型，搭建相应的实验平台。实验设备包括一台双三相永磁同步电机、六相电压型逆变器、直流电源和TMS320F28335微控制器，如图10所示。

图10 实验设备

ADC的采样频率和逆变器的开关频率都被设为10kHz。直流母线电压设置为64V。一组高频余弦电压信号(fh=500Hz,Uh=3.2V)被注入到ABC绕组估测的d轴。

当转子旋转速度给定为120r/min，有PR控制时，转子实际位置、转子估计位置、转子位置估计误差如图11所示。可以看到转子位置估计误差接近于0，转子位置估计非常精确。意味着PR控制并没有影响转子位置的跟踪性能。

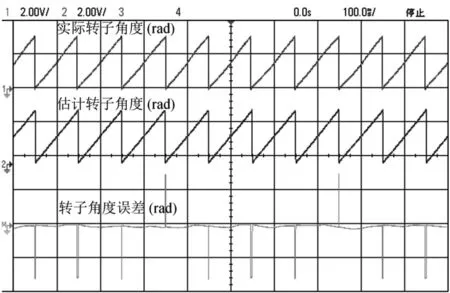
图11 转子位置估计性能

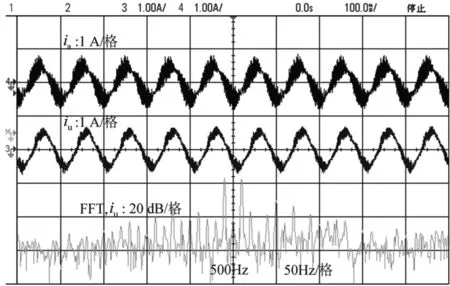
图12 无PR控制时A相电流、U相电流及U相电流FFT

当给定转子速度为120r/min时，无PR控制时，A相电流和U相电流如图12所示。根据U相电流的FFT，可以清楚的看到U相中存在500Hz的高频感应电流，由于叠加了电流角频率，因此频率有偏移。且A相电流的高频分量要比U相电流的高频分量要大，验证了式(6)。另外A相电流比U相电流相位超前30°，验证了文献[8]的理论分析。

加入PR控制后，A相电流和U相电流如图13所示。根据U相电流的FFT，可以清楚的看到U相电流中几乎没有500Hz的高频感应电流，意味着PR控制可以完美的抑制ABC绕组注入的高频电压信号在UVW绕组产生的高频感应电流。

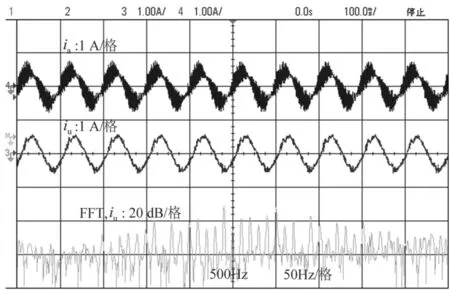
图13 有PR控制时A相电流、U相电流及U相电流FFT

5 结 论

本文提出了基于PR控制的改进单绕组高频注入的双三相永磁同步电机无位置传感器控制。通过PR控制，抑制ABC绕组注入的高频电压信号在UVW绕组产生的高频感应电流。根据系统参数和注入的高频信号频率，设计了最优的PR参数。仿真和实验结果验证了PR控制可以有效地抑制UVW绕组中的高频电流响应，提升了双三相永磁同步电机无位置传感器控制的性能。