混合励磁直线磁悬浮同步电动机三维有限元分析
蓝益鹏,李增乐
(沈阳工业大学 电气工程学院,沈阳 110870)
0 引 言
在传统的数控机床驱动装置是“旋转电动机+滚珠丝杠”的配合方式,由于存在中间传动装置的,大大的限制了数控机床驱动装置的速度、精度和效率。相比之下,直线电机的传动性能更加优越,将直线电机作为驱动装置,既可以实现直接驱动,还省去中间传动装置,具有高动态响应,高精度,噪音低,行程长等优点,但是直线同步电机有法向力的存在对系统的导轨影响和摩擦损耗会影响机床进给系统的精度[1-2]。
磁悬浮技术与直线电机相结合应用于高精度直线驱动的数控机床的研究,目前主要以电磁铁实现数控机床进给平台的悬浮,以达到无摩擦进给,但是结构相对复杂,成本昂贵[3]。因此,直线磁悬浮电动机作为数控机床直线驱动的装置则有着重要意义。利用直线电机的法向力使电机实现悬浮,直线磁悬浮同步电动机具有直线同步电动机响应速度快、定位精度高、零传动进给等优点,同时根本上消除了数控机床摩擦问题。控制悬浮高度稳定,选用电励磁直线磁悬浮电动机和混合励磁直线磁悬浮同步电动机作为驱动装置。
在本研究中,分析混合励磁直线磁悬浮同步电动机(Hybrid Excitation Linear Maglev Synchronous Motor, HSLMSM)的特性。HELMSM的物理特性是混合激励,它结合了永磁体的高能量密度和易于实现的电激励的可控性。HSLMSM具有提高悬浮气隙高度、降低平台总重量和显著改善热条件等优点[5]。HELMSM的有效气隙很大,它包括具有高性能的永磁体高度和定子的大槽。此外,由于该装置是一个三维(3-D)模型,泄漏通量表现出复杂的行为,需要对三维电磁场计算进行详细的研究。因此,采用三维有限元法(FEM)计算悬浮力和推力,以避免计算误差[6]。并验证HELMSM在数控机床上应用的可行性。
1 HELMSM 结构与数学模型
1.1 HELMSM的基本结构
HELMSM由定子和动子构成。定子部分与基座相连,而动子与运动平台是一体。定子槽形为开口形,便于安放励磁绕组,槽口用金属槽楔固紧,每个槽中安放两组线圈,两组线圈反方向缠绕在相邻的两个大齿上,永磁体以及弧形导磁金属块安装在大齿上,大齿中心即为磁极的中心。动子由动子铁心结构和采用单层迭绕的三相绕组构成。图1显示了进给平台三维结构图,图2为HELMSM的独立结构。

图1 进给平台三维结构图

图2 混合励磁直线磁悬浮同步电动机的结构示意图
该电机由安装在定子上的高性能永磁体对动子产生的吸引力实现悬浮。为了实现稳定的悬浮,必须通过永磁体周围的直流励磁线圈来调节永磁体的磁通量。
动子的铁心都是硅钢片叠加而成,以减少涡流的影响。永磁体的选择规格是为了允许在额定气隙中无需任何额外电力的情况下使得进给平台实现稳定悬浮。为保证HELMSM的设计合理和最佳,选用的永磁材料为N35SH,其计算剩磁密度1.15T,计算矫顽力为882kA/m,相对回复磁导率为1.04[7]。表1列出了HELMSM的基本设计参数。

表1 HELMSM基本参数
1.2 HELMSM的电磁力数学模型
在一定的假设条件下,建立HELMSM的数学模型,电磁推力和悬浮力方程。
采用id=0的控制策略,由电压方程和磁链方程推导出电磁推力和悬浮力的经验公式分别为[8]
(1)
(2)
式中,Fx、Fy为电磁推力与悬浮力;id、iq分别为电枢直轴电流和电枢交轴电流;if为磁极励磁电流;ψpm为永磁体磁链;Lmd为定子在直轴的互感;g为气隙高度,Lq为电枢绕组交轴自感。
一般情况下,if,iq在一定范围内调节时,Lmdif和Lqiq比ψpm小得多,因此,式(1)和式(2)可简化为
(3)
(4)
电磁推力Fx主要与交轴电流iq有关,法向吸磁力Fy主要与励磁电流if有关。调节iq能够控制电磁推力,调节if能够控制法向吸磁力。
2 HELMSM的磁场三维有限元分析
由于二维(2-D)有限元分析模型仅仅描述了电动机的中心截面,不能表达漏磁的复杂行为,为了研究电动机的基本特性更为准确[9-10],采用三维有限元分析方法对HELMSM的磁场分布和电磁力进行分析。在三维有限元计算中,采用了商用有限元软件“ANSYS-Maxwell”进行实验研究。根据电动机的基本数据画出电动机的三维模型,三维模型的计算网格如图3所示。模型由351256个四面体单元组成。

图3 三维有限元模型及计算网格
计算时间和可达到的误差极限是三维仿真的重要评价标准。为了获得较小误差的有用结果,电动机的气隙必须至少分为3层。图4显示了当气隙高度为2mm时,无电枢电流和无直流励磁电流时,定子和动子铁心中的磁通矢量分布。在侧面有一个大的漏磁通与动子的铁心相连。这种横向通量可能导致二维有限元计算中出现误差[6]。

图4 磁通矢量分布
图5为直流励磁电流为0A时,动子铁心、定子铁心和永磁体的三维法向气隙磁通密度分布,动子中心处的法向磁通密度约为0.64T,侧边处的法向磁通密度约为0.25T。

图5 气隙磁通密度分布
图6显示了3个不同直流励磁电流值(0A、+10A和-10A)的气隙磁通密度分布。由于该电动机的拓扑结构,气隙磁通密度分布为非正弦分布,包含大量谐波含量。如图所示,磁通密度的大小随直流励磁电流的方向而减弱或增强。磁通密度的最大值为0.87T,最小为0.54T。
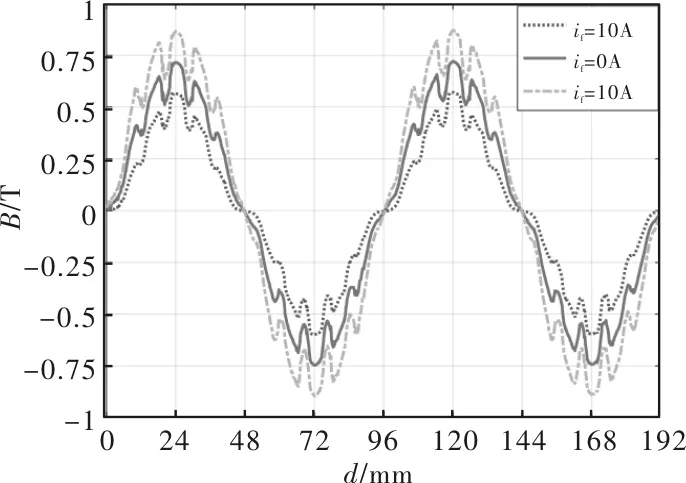
图6 不同直流电流的气隙磁通密度
为了调整HELMSM的磁通控制水平,磁通控制系数α为[11]
(5)
式中,FY0为无直流电流产生磁场时的悬浮力, 是施加直流时的磁通密度。

图7 悬浮力与直流励磁关系图
图7说明了悬浮力控制能力与直流励磁的关系。从图7可以看出,在直流电流变化较小的情况下,可以实现相对宽的磁通控制范围。当施加±10 A的变化时,磁通控制(无负载)在磁通增强模式(高悬浮)下的范围约为59.9%。在弱磁模式下(低悬浮力至-58.3%。此外,图中还显示了模型的直流励磁电流在±10A范围内基本保持线性电动机磁路未达到饱和,电动机的磁通控制能力良好。悬浮力和励磁电流基本保持线性关系,验证了悬浮力表达式的正确性。
图8为电磁推力与交轴电流变化的曲线,从图中可以看出两者基本保持线性关系,验证了电磁推力表达式的正确性。

图8 电磁推力随交轴电流变化曲线
3 结 论
(1)研究了HELMSM的基本结构,并对其运行原理进行论述,给出了HELMSM在d-q坐标系中的电磁推力和悬浮力的解析表达式。
(2)搭建了HELMSM的三维拓扑结构的有限元模型,并进行有限元计算,分析了电动机的磁场分布以及电磁推力和悬浮力的特性分析,验证了if,ig在一定范围内调节时,电磁推力和悬浮力的解析表达式的正确性。
(3)电磁推力和悬浮力,调节范围广,控制相对简单,更适于数控机床的零摩擦进给驱动,为数控机床的磁悬浮直接进给技术的研究提供了科学依据。

