采用滑动平均低通滤波的脉振高频信号注入法在表贴式永磁同步电机无位置传感器控制中的应用

郭增冰，臧 珂，胡勤丰

(南京航空航天大学，南京 211100)

0 引 言

永磁同步电机的无位置传感器控制是当前交流传动领域的一个研究热点。无位置传感器控制方法主要分为两大类：第一类是适用于中高速的方法，第二类是适用于零低速的方法[1-2]。第一类方法通常是通过提取电机的反电势来获得位置信号，该方法目前已经能达到良好的控制效果[3-4]。第二类方法通常是基于电机的凸极性，利用凸极引起电机定子电感的变化来获得转子位置[5]。

表贴式永磁同步电机的交直轴电感几乎相等，导致其利用电机的凸极性获得转子位置的难度较大。文献[6]提出了一种适用于表贴式永磁同步电机无位置传感器控制的低频信号注入法，但该方法动态响应慢，动态过程转速和转矩脉动较大。韩国首尔大学的Sul S K教授于1997年提出脉振高频信号注入法，并于2003年利用该方法实现了表贴式永磁同步电机的低速无位置传感器控制[7]。该方法利用电感的非线性饱和特性，通过注入信号，从而使电机获得一定的凸极率。但是，脉振高频信号注入法也存在一些问题，比如转矩脉动和噪声较大[8-9]，滤波器的使用造成系统响应慢，动态性能差[10-12]，带载时位置观测精度下降[13]等等。

本文首先分析了脉振高频信号注入法无位置传感器控制系统的实现原理，然后针对电流环巴特沃斯低通滤波器不能完全滤除电流回路中的高频电流导致电流调节器产生相应的响应从而削弱注入的高频电压的问题，使用了滑动平均低通滤波器，该滤波器能完全滤除特定频率的信号，通过选择合适的系统参数，便可以完全滤除电流中的高频信号。理论和实验都证明了使用该滤波器的脉振高频信号注入法在表贴式永磁同步电机无位置传感器控制中的有效性。

1 脉振高频信号注入法原理

1.1 表贴式永磁同步电机的饱和凸极性

永磁体的磁导率与空气磁导率几乎相等，因此，表贴式永磁同步电机的直轴电感与交轴电感很接近，属于隐极式电机。图1为永磁电机直轴磁路Ψ-i特性曲线，在设计电机时，通常将直轴磁路工作点设计在永磁体临界饱和处，如图A点所示，if为永磁体磁链Ψf的等效励磁电流，当直轴通入一定的正向电流时，永磁体处于饱和状态，直轴电感会相应的减小，反之，当直轴通入一定的反向电流时，永磁体处于去磁状态，磁路不饱和，直轴电感变化很小。而交轴磁路的工作点在原点，磁路工作在线性区，不会出现磁路饱和的情况，交轴电感的变化可以忽略不计。因此，可以通过向表贴式永磁同步电机直轴通入一定的正向电流使表贴式同步永磁电机呈现出饱和凸极性，即直轴电感的非线性饱和特性。

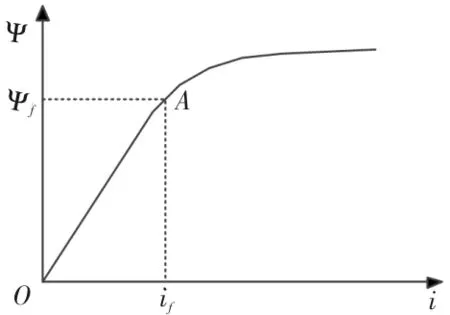
图1 直轴磁路Ψ-i特性曲线

1.2 脉振高频信号注入法提取位置的原理

永磁同步电机在dq轴同步旋转坐标系下的电压方程为

(1)

首先建立实际的同步旋转坐标系和估计的同步旋转坐标系如图2所示。

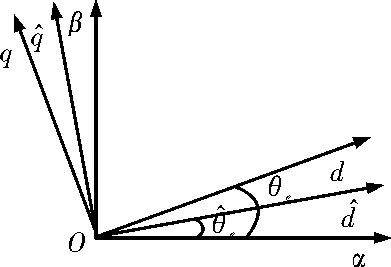
图2 实际转子和估计转子同步旋转坐标系

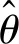
(2)

脉振高频信号注入法一般用于电机的无位置起动和低速运行，在此类情况下，注入的高频信号角频率ωh远大于电机的基波角频率ωe，而且高频时电抗比电阻要大很多，所以电机的高频电压方程为

(3)

定义转子位置误差Δθ为

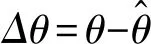
(4)

估计的同步旋转坐标系与实际的同步旋转坐标系之间的坐标变换公式为

(5)

(6)

结合式(2)至式(6)可以得到在估计的同步旋转坐标系下的高频电流响应为

(7)

其中，L=(Ld+Lq)/2为平均电感，ΔL=(Ld-Lq)/2为半差电感。可以看出，只要dq轴电感不相等，电机的dq轴高频电流响应中就会含有转子位置误差信号，而且当转子位置误差为零时，q轴高频电流幅值也为零，因此，可以对q轴高频电流进行适当的处理，提取出高频电流幅值，再通过调节器使其收敛至零，这样，转子的估计位置便收敛到了实际位置。

电机的实际电流包含基波电流和高频电流，电流环反馈只需要基波电流，通常通过一个低通滤波器滤除高频电流分量和逆变器高频开关带来的谐波分量。提取位置信号需要高频电流，首先，让电流通过一个高通滤波器，滤除电机的基频电流分量，然后，再将滤波之后的电流与正弦调制波sin(ωht)相乘，最后，经过一个低通滤波器，便可以提取出高频电流幅值为

(8)

此低通滤波器还可以滤除逆变器高频开关带来的谐波分量。将f(Δθ)作为转子位置观测器的输入信号，选择合适的调节器参数使f(Δθ)收敛至零，便可以使转子估计位置收敛到实际位置(需进行磁极极性判断，但本文不做阐述)。转子位置观测器的结构如图3所示。

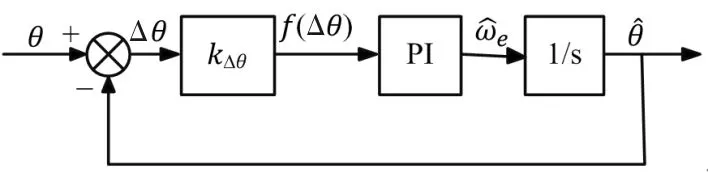
图3 转子位置观测器结构框图

脉振高频信号注入法无位置传感器控制系统框图如图4所示。

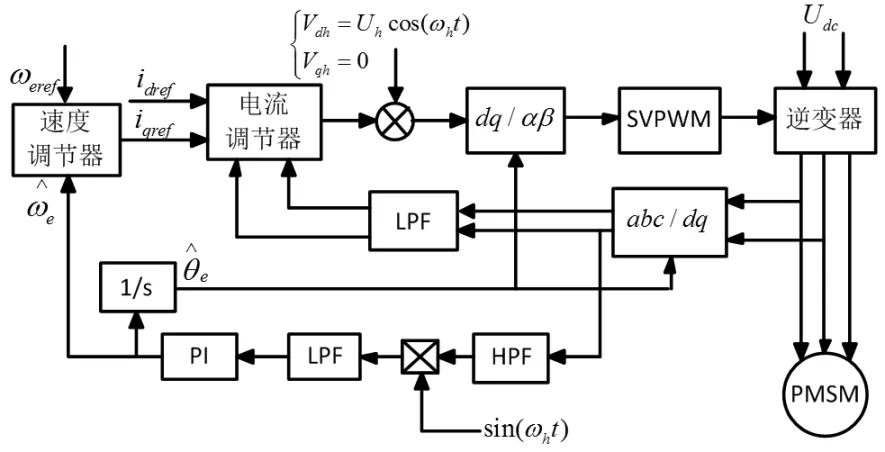
图4 脉振高频信号注入法无位置传感器控制系统框图

2 滑动平均滤波在脉振高频信号注入法中的应用

2.1 巴特沃斯低通滤波器存在的问题

在d轴施加了高频脉振电压之后，dq轴电流中都会出现相应的高频电流分量，一般让dq轴电流通过一个低通滤波器之后，再反馈给电流调节器，通常，该低通滤波器为巴特沃斯型低通滤波器。巴特沃斯滤波器在其通频带内有着最大的平坦特性，而且设计比较简单，在滤波性能上也没有明显的缺点，所以在电机控制的信号处理中使用较多[14]，巴特沃斯低通滤波器的幅频响应为

(9)

式中，n为滤波器的阶数，ωc为其截止角频率，当n=1，ωc分别为1256rad/s和3140rad/s时(对应频率分别为200Hz和500Hz)，巴特沃斯低通滤波器的幅频特性曲线分别如图5和图6所示。

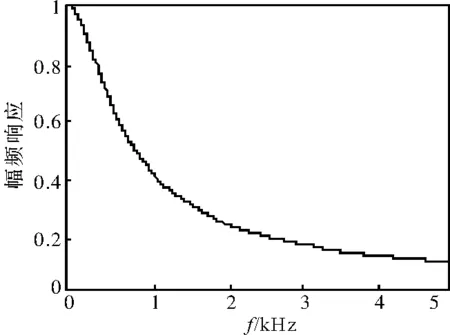
图5 一阶巴特沃斯低通滤波器幅频特性，ωc=1256rad/s

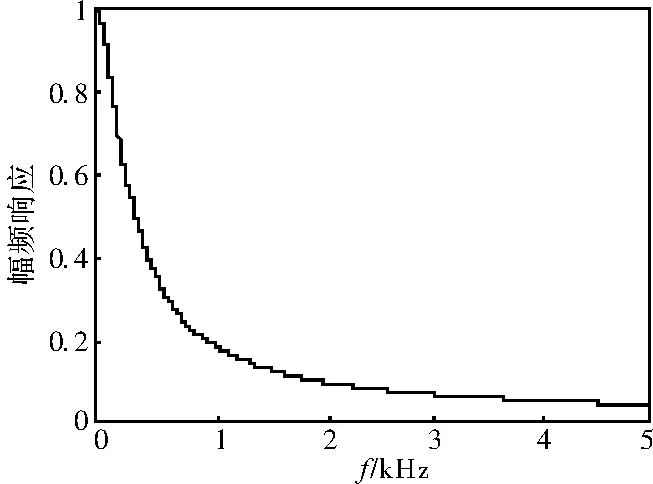
图6 一阶巴特沃斯低通滤波器幅频特性，ωc=3140rad/s

从图中可以看出，巴特沃斯低通滤波器幅频特性比较平滑，而且对高频分量也有较高的衰减，但是巴特沃斯低通滤波器并不能完全滤除高频电流信号，这样电流调节器便会产生相应的高频响应来削弱这些高频电流分量，最终导致了dq轴参考电压中也出现了相应的高频电压从而削弱注入的脉振高频电压。若滤波器截止频率取得较低，则会造成比较大的延时，影响系统的动态性能。

2.2 滑动平均低通滤波器原理

滑动平均是一种求当前时刻之前N个量平均值的算法，其差分方程为

(10)

也可以表示成

(11)

对上式左右两端进行Z变换，可以得到

(12)

从而得到

(13)

式(13)便为采样深度为N的滑动平均低通滤波器的脉冲传递函数，当采样周期为Ts=0.0001s，采样深度分别为N=5和N=10时，G(z)幅频特性曲线分别如图7和图8所示，可以看出滑动平均低通滤波器在其阻带内的幅频特性曲线有较大的起伏，但是在频率f为1/(NTs)的整数倍时，对应的幅频响应为零。所以可以通过选择合适的高频信号频率和滤波器采样深度，将电流环路中的高频信号完全滤除。

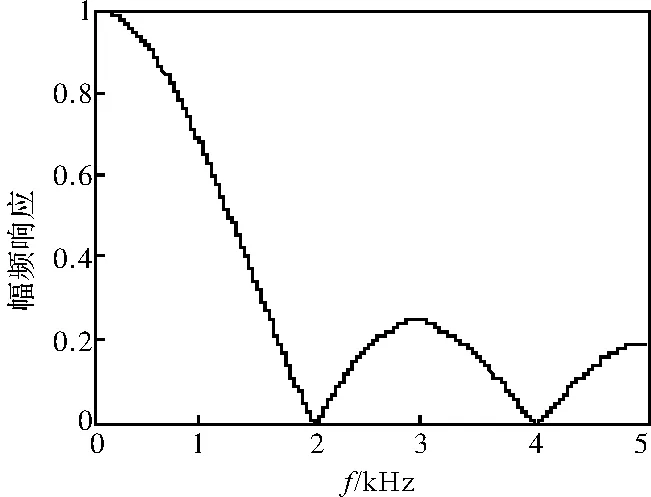
图7 滑动平均低通滤波器幅频特性，Ts=0.0001s，N=5

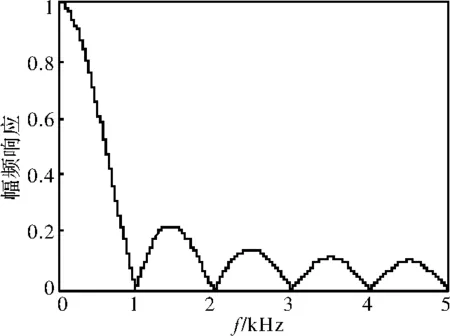
图8 滑动平均低通滤波器幅频特性，Ts=0.0001s，N=10

3 实验验证

为了验证算法的可行性，搭建了基于TMS320F28335的电机驱动控制平台，进行算法的在线调试。所用表贴式永磁同步电机的参数如表1所示。

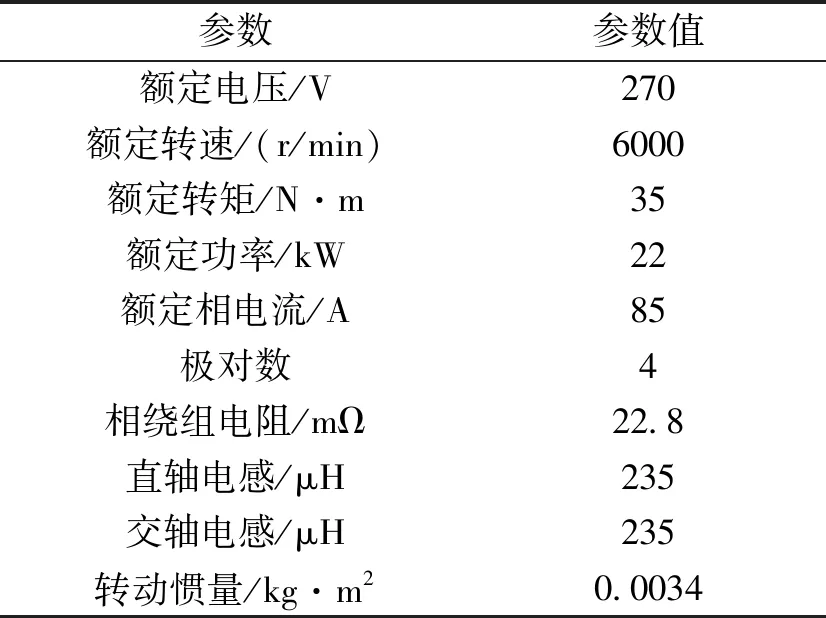
表1 表贴式永磁同步电机参数

其中，转子的实际位置和实际转速由旋转变压器提供，用以和估计位置和估计转速进行对比，PWM频率选择10kHz，注入高频电压信号的频率为1kHZ，滑动平均滤波器的采样深度为N=10，这样，理论上可以完全滤除电流中1kHz的高频信号。

3.1 空载实验

图9为电机以100r/min空载起动的波形，可以看出，转速在起动阶段稍有延迟，但转子的估计位置和估计转速都能较好跟随实际位置和实际转速。

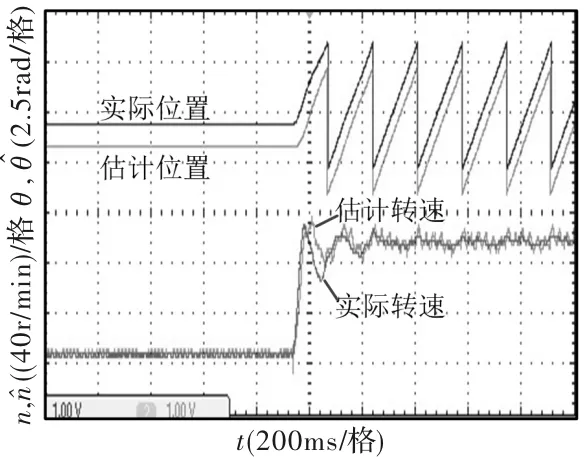
图9 空载起动波形

3.2 带载实验

图10为电机带5 Nm负载，以100r/min起动的波形，图11为起动时位置波形的局部放大图，图12和图14分别为电机在100r/min时突加5 Nm负载和突卸5 Nm负载的波形，图13和图15分别为其位置波形的局部放大图，从图中可以看出，起动时间和突加突卸负载之后转速回到稳定的时间较长，但转子估计位置和转速都能跟随实际位置和转速。

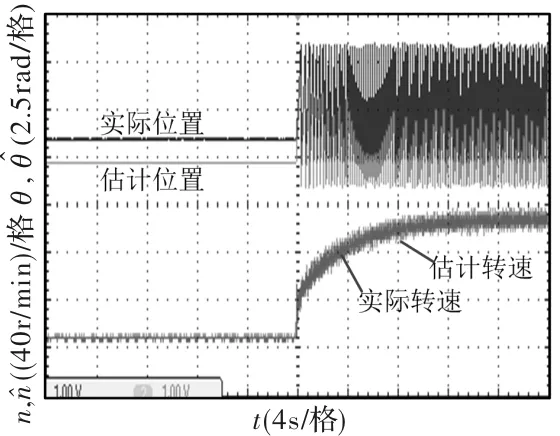
图10 带5Nm负载起动波形

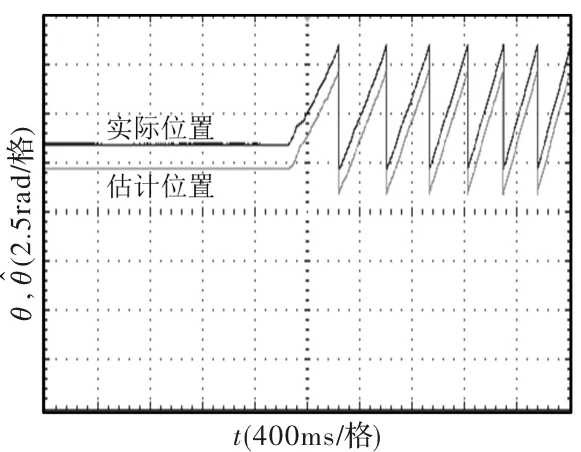
图11 带5Nm负载起动位置局部放大波形

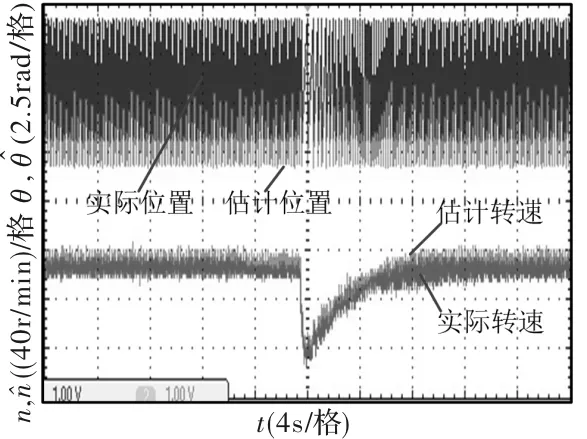
图12 突加5Nm负载波形

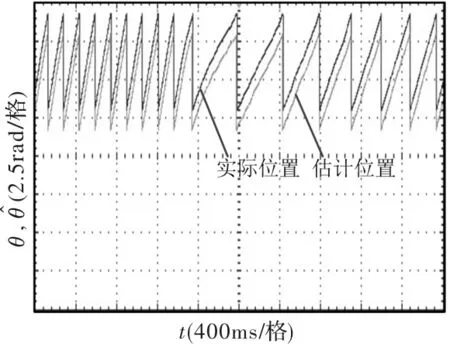
图13 突加5Nm负载位置局部放大波形

图14 突卸5Nm负载波形

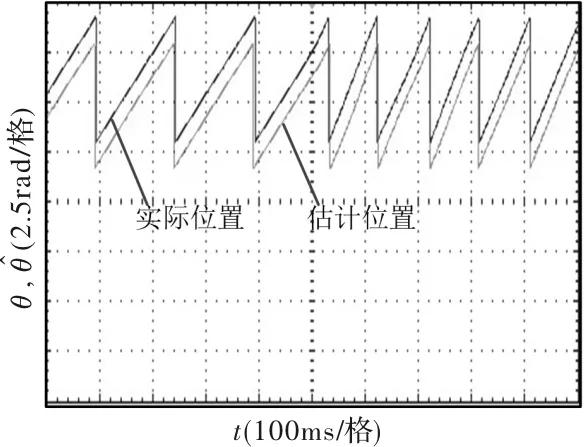
图15 突卸5Nm负载位置局部放大波形

图16和图17分别为使用滑动平均低通滤波器和使用巴特沃斯低通滤波器带5Nm负载起动时dq轴电流波形。从图中可以看出，滑动平均低通滤波器能有效地滤除电流环路中的高频分量。

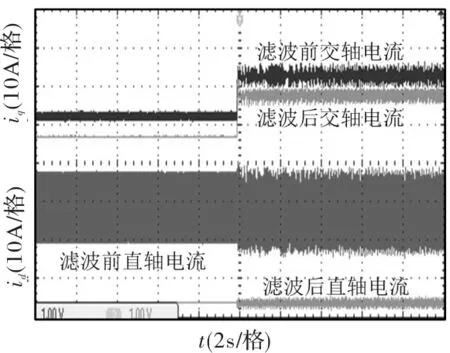
图16 使用滑动平均低通滤波器dq轴电流波形

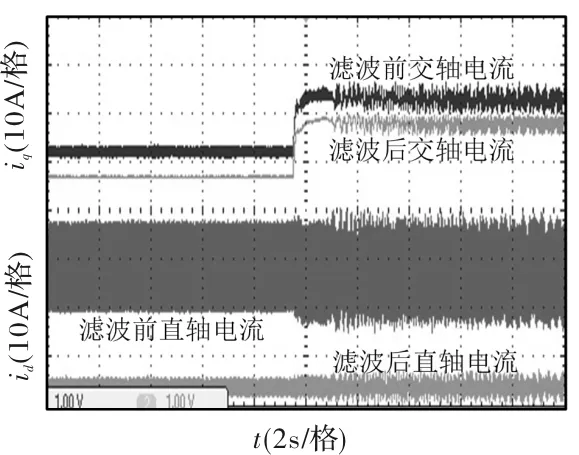
图17 使用巴特沃斯低通滤波器dq轴电流波形

4 结 论

本文提出了一种使用滑动平均低通滤波器的脉振高频信号注入法，并使用该方法实现了一台表贴式永磁同步电机的无位置传感器控制，理论分析和实验结果都表明，该方法能有效地滤除电流中的高频分量，使用该方法的脉振高频信号注入法在电机起动，突加突卸负载时转子估计位置和转速都能较好跟随实际位置和转速。