水面无人艇领航—跟随固定时间编队控制
李贺,王宁,薛皓原
大连海事大学 船舶电气工程学院,辽宁 大连 116026
0 引 言
近些年,水面无人艇(Unmanned surface vehicle,USV)在军民用领域扮演的角色越来越重要,其可遂行情报侦察、水域环境检测、海图绘制等任务[1]。但是,当面临复杂的水域环境以及多样性的作业任务时,单个USV显得势单力薄,而多USV协同控制因其具有效率高、覆盖广、鲁棒性强等优势,逐渐成为研究的热点[2]。在多USV协同控制领域,研究热点之一便是编队控制,主要策略有:图论[3]、基于行为的控制策略[4]、虚拟领航者[5]、神经网络[6]和领航—跟随控制策略[7]等。在上述几种策略中,领航—跟随控制策略具有控制结构简单、可扩展性好等优势,因而得到了更加广泛的应用。该策略中,跟随USV只需接收领航USV的动态信息,便能够实现稳定的编队队形。
领航—跟随USV编队控制系统中,其稳定性将会受到复杂的外界环境扰动影响(主要为水域环境中的风、浪、涌等干扰),这给USV编队的稳定控制带来了极大的困难。滑模控制技术因其具有较强的抗不确定性和抗扰性,已经在随机系统、刚体系统、海洋装备等领域得到了较为广泛的应用[8]。常见的滑模技术主要有传统的渐进收敛滑模[9]、积分滑模[10-11]、终端滑模[12]、非奇异终端滑模[13-14]等。为了进一步处理复杂的外界扰动,以前的研究主要采用了如非线性扰动观测器[15]、降维扰动观测器[16]等。近些年,有限时间扰动观测器(finite-time distribute observer, FDO)技术逐渐成为研究热点,Wang等[17-24]对FDO进行了尝试应用,取得了显著的成果。相比于传统的扰动观测器,FDO能够对扰动实现快速、精确的辨识。但是,FDO技术在USV编队控制领域鲜有应用,具有潜在的研究价值。
在领航—跟随USV编队控制中,为了更好地保证编队系统的响应特性,收敛速率是首要考虑的控制指标。早期的文献针对一阶多智能体系统的线性一致性拓扑,提出了代数连通图的概念,并运用渐进收敛算法证明了其有效的收敛性[25]。然而,渐进收敛算法存在收敛时间不可预测的不足,导致了系统稳定性的不可预测。鉴于此,随后的文献更多采用有限时间收敛算法,求解单智能体或者多智能体编队的收敛性问题[26-28],该算法极大改善了以往算法的跟踪精度和收敛速度。近几年,作为有限时间算法的扩展,固定时间控制算法逐渐被引入多智能体编队控制领域。固定时间控制算法由Polyakov[29]首次提出,该算法能够实现有限时间收敛,并且其收敛时间的上界可以通过数学方法计算得到。Zuo等[30-32]在随后的研究中分别运用固定时间算法在一阶、二阶以及高阶多智能体系统中进行了尝试应用,证明了其具有更好的精准性和收敛性。
基于此,本文将针对复杂扰动下的领航—跟随无人艇编队系统,提出基于固定时间的编队控制策略。首先,设计基于积分滑模的固定时间跟踪控制(ISM-FTC)策略,将其应用于跟踪控制子系统中;然后,引入基于有限时间扰动观测器的固定时间编队控制(FDO-FFC)策略,将其应用于编队控制子系统中,对复杂扰动下的领航—跟随编队系统进行精确控制;接着,通过Lyapunov函数证明所设计控制器的理论可行性;最后,通过仿真实验,验证所提出设计方法的可行性。
1 预备知识和问题描述
1.1 预备知识
引理1:对于非线性系统:

1.2 问题描述


本文旨在设计一种固定时间编队控制器,在固定时间内,控制器不仅能够驱动跟踪控制子系统精确跟踪期望的轨迹,且能够驱动编队控制子系统快速形成期望的队形并保持队形,从而实现USV领航—跟随编队快速、精确的控制。
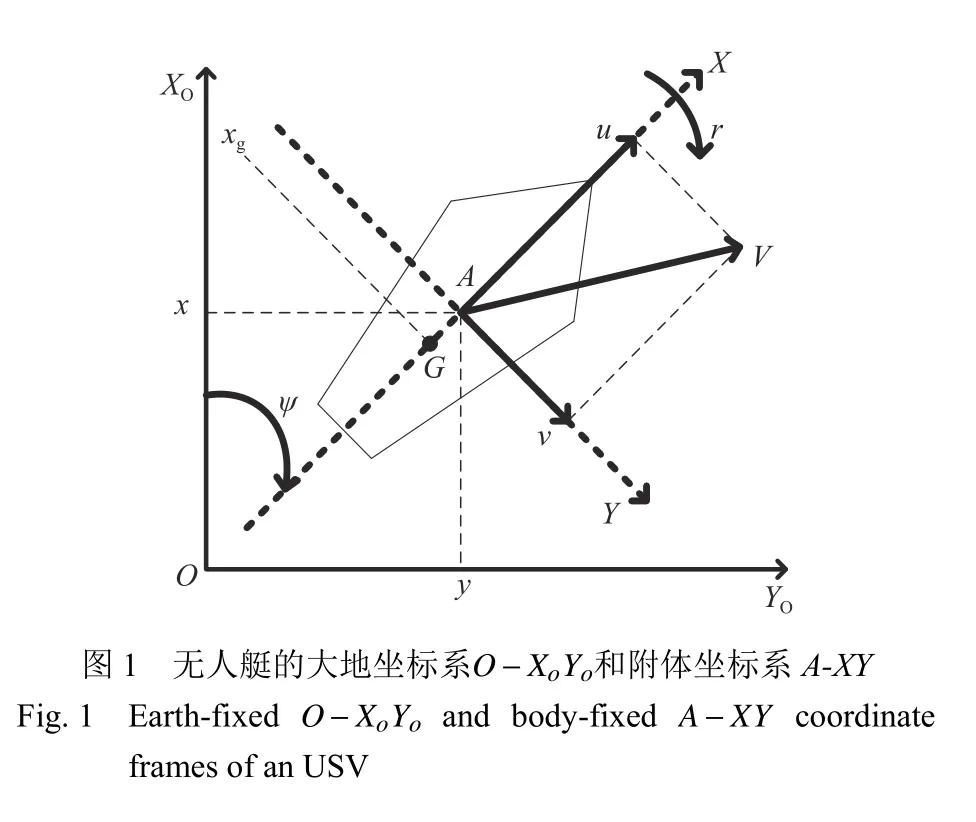
2 控制系统设计与稳定性分析
领航—跟随编队控制方案框图如图2所示,为保证编队系统设计的整体性,将编队系统划分为跟踪控制子系统和编队控制子系统,分别设计控制器,从而保证编队系统的有效性。

图 2 领航—跟随编队控制方案框图Fig. 2 The block diagram of the leader-follower control scheme


2.1 跟踪控制子系统控制器设计
设计跟踪控制子系统控制器,从而保证编队系统对期望轨迹的精确跟踪,同时为编队控制子系统提供控制输入信号。


2.2 编队控制子系统控制器设计



3 仿真研究
为了验证固定时间控制策略的有效性,利用经典的Cybership II试验模型进行仿真实验。设计1艘领航USV和2艘跟随USV组成编队系统,进行仿真验证。


表 1 模型的初值Table 1 The initial values of the model
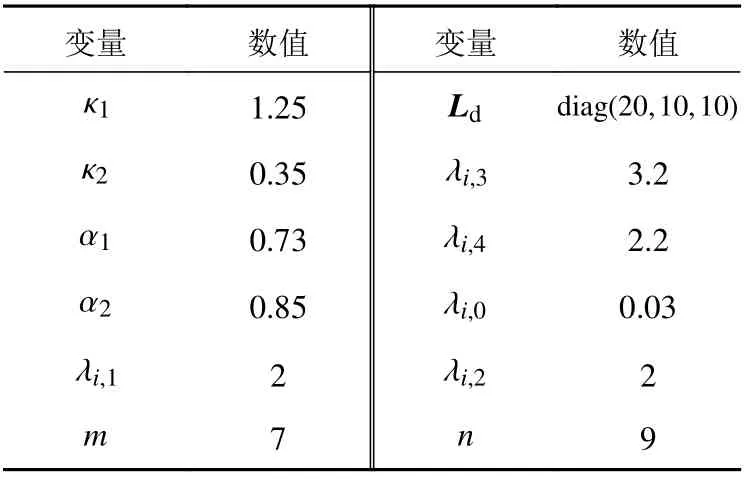
表 2 各参数的取值Table 2 The values of each parameter
仿真结果如图3~图12所示。图3显示了跟踪控制子系统精确跟踪的期望轨迹,可见编队控制子系统能够精确形成和维持领航—跟随编队队形;图4~图5分别显示了编队系统的位置和速度跟踪随时间的变化曲线,可见在5 s内各个维度完成了期望的任务,并且收敛时间小于设定时间的上限;图6~图8分别显示了领航USV和2个跟随USV 的控制输入随时间的变化曲线,验证了控制器能够在固定时间内趋于稳定;图9~图10分别显示了2个跟随USV的外界扰动曲线以及FDO
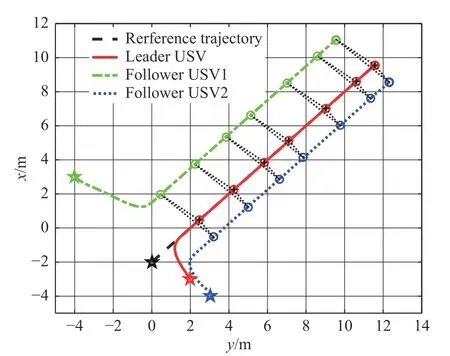
图 3 USV编队轨迹图Fig. 3 The trajectories of USV formation
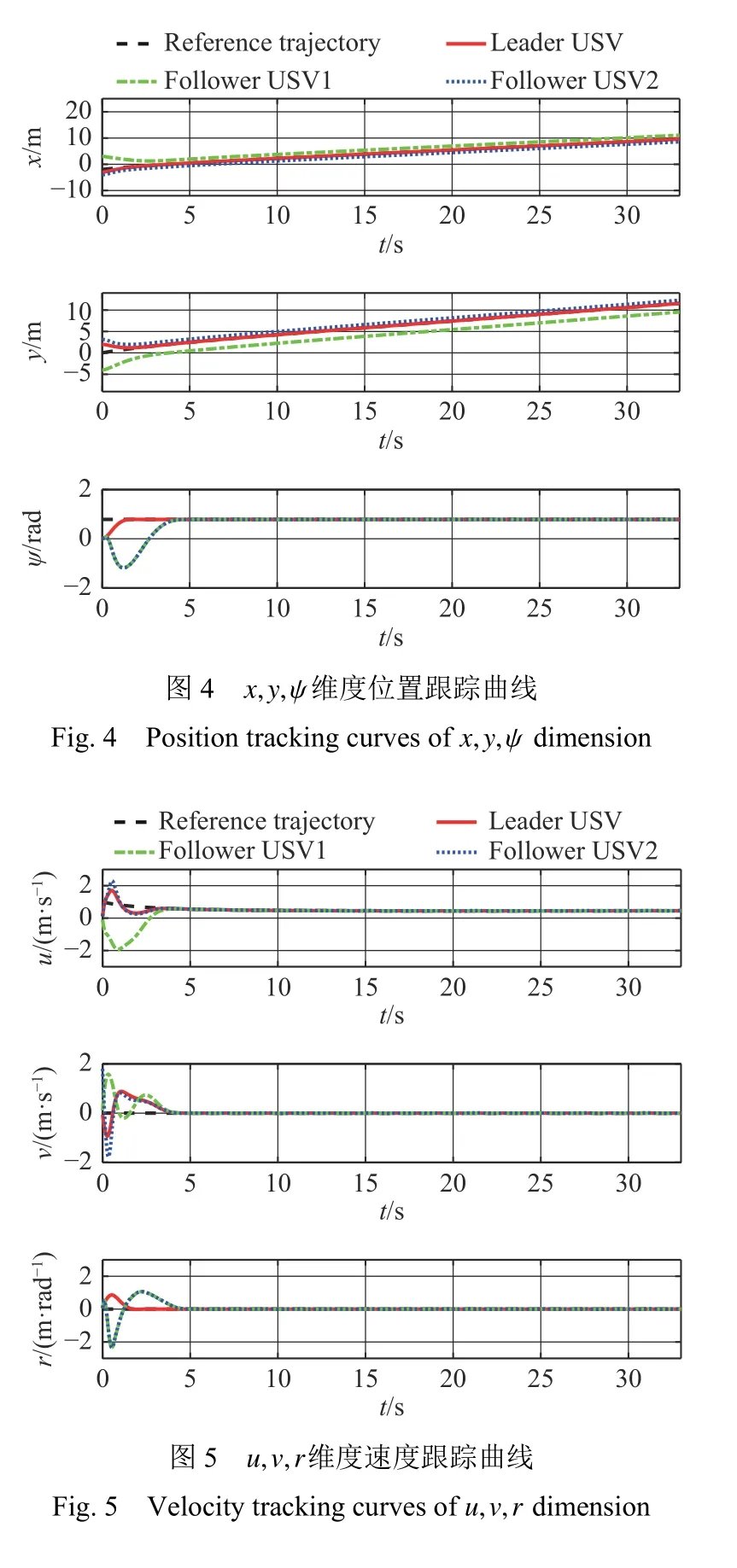



图 12 有限时间和固定时间方法对比(2)Fig. 12 The contrast of methods of finite-time and fixed-time (2)
4 结 论
本文针对领航—跟随USV编队系统在复杂环境扰动下的控制问题,结合积分滑模和反步控制技术,提出了FTC策略。在跟踪控制子系统中,设计了ISM-FTC控制器,使得领航USV精确跟踪期望轨迹;在编队控制子系统中,设计了FDOFFC控制器,使得跟随USV精确保持对领航USV的相对位置,尤其是存在外界扰动的情况下,仍然能够确保稳定的领航—跟随USV编队队形。采用Lyapunov稳定性理论,证明了闭环编队控制系统的稳定性。仿真结果表明,在复杂外界扰动下,所设计的USV编队控制系统能够精准跟踪期望的轨迹并快速形成和保持期望的编队队形。本文设计的固定时间控制策略为USV编队控制提供了新的设计方案。

