基于有限元法的喷水推进轴系回旋振动分析

马召召，周瑞平*，刘琪，范君浩，胡云飞

1 武汉理工大学 能源与动力工程学院，湖北 武汉 430063

2 中国舰船研究设计中心，湖北 武汉 430064

0 引 言

船舶喷水推进装置具有变工况适应能力强、推进效率高、操纵性能好等优点，随着喷水推进技术的不断发展，其军事价值逐渐受到各国海军的重视，已相继应用于各类新型舰船，例如美国“海狼”级（SSN-21）攻击型核潜艇、德国F-124型护卫舰、英国“海魂”（Seawraith）号隐身护卫舰等[1-2]。与民用、商用船舶相比，军用舰船对各项性能指标的要求更严格，对高速喷水推进舰船而言，轴系回旋振动的影响是不容忽视的一项指标。通过改变喷射水流的流量及方向，即可实现喷水推进舰船的灵活控制，但在船艉处不均匀伴流场的作用下，叶轮上的流体激振力将更为复杂，进而加剧喷水推进轴系的回旋振动。回旋振动主要产生于轴系尾部，不仅会产生噪声，严重时，还将导致艉轴承严重发热、过度磨损、轴裂、轴断及机损等事故。

为避免喷水推进轴系产生有害的回旋振动，有必要综合考虑各种因素，对其回旋振动特性进行深入研究。陈之炎等[3-4]分析了回旋振动的机理、特点和计算方法。周瑞平[5]基于传递矩阵法，利用VB语言编制了具有工程应用价值的回旋振动计算软件。刘刚等[6]基于传递矩阵法，研究了回旋振动的各种影响因素，并提出了参数选取方法，可为回旋振动特性分析提供依据。然而，当轴系转速过高、轴系较长以及支承较多且刚度较大时，采用传统的传递矩阵法可能会出现数值不稳定及漏根现象，从而导致回旋振动的计算结果不准确。因此，为了提高计算精度，可以考虑采用基于有限元方法的计算模型。王苏等[7]利用ANSYS转子动力学模块建立了轴系有限元模型，并分析了回旋振动对轴系的影响。王正兴等[8]利用VB和ANSYS参数化设计语言混合编程，开发了回旋振动计算软件。张伟等[9]利用有限元方法研究了陀螺效应及不同支撑刚度对气垫船轴系回旋振动的影响。

针对喷水推进轴系，本文拟基于ANSYS仿真软件平台，利用ANSYS命令流建立轴系参数化有限元模型，开展多载荷步模态仿真分析，计算轴系的固有振型、回旋振动临界转速和轴系在临界转速下的涡动轨迹，并分析推力轴承布置方式和轴承支承刚度对喷水推进轴系回旋振动的影响。通过阐述基于有限元法计算喷水推进轴系回旋振动的完整方法，可为喷水推进轴系的安全运行提供理论依据。

1 有限元模型

本文以某40 m双体船喷水推进轴系为研究对象。该轴系为内置式喷水推进传统式轴系[10]，其推进泵安装于船体内部，配置了重量为118 kg的6叶片叶轮，转速为867 r/min。轴系布置如图1所示，轴长7.45 m，由叶轮驱动轴、中间轴、齿状联轴节、连接短轴和齿轮箱输出轴等组成。其中中间轴采用碳纤维复合材料，其材料属性为：杨氏模量E=1.81×1011N/m2，泊松比μ=0.28，密度ρ=1 760 kg/m3。其他轴段使用的材料为碳钢，其材料属性为：杨氏模量E=2.0×1011N/m2，泊松比μ=0.30，密度ρ=7 850 kg/m3。该轴系共计有5个轴承，分别为后支撑轴承、赛龙艉轴承、推力轴承、齿轮箱前轴承和后轴承，其中后支撑轴承为水润滑轴承，独立于轴密封之外，可以有效防止其被润滑油污染；推力轴承位于叶轮轴密封之前，其基座固定于船体。轴承支承的刚度取为经验值，其中后支撑轴承支承刚度k1=7.1×108N/m，其他轴承支承刚度k2=1×109N/m。

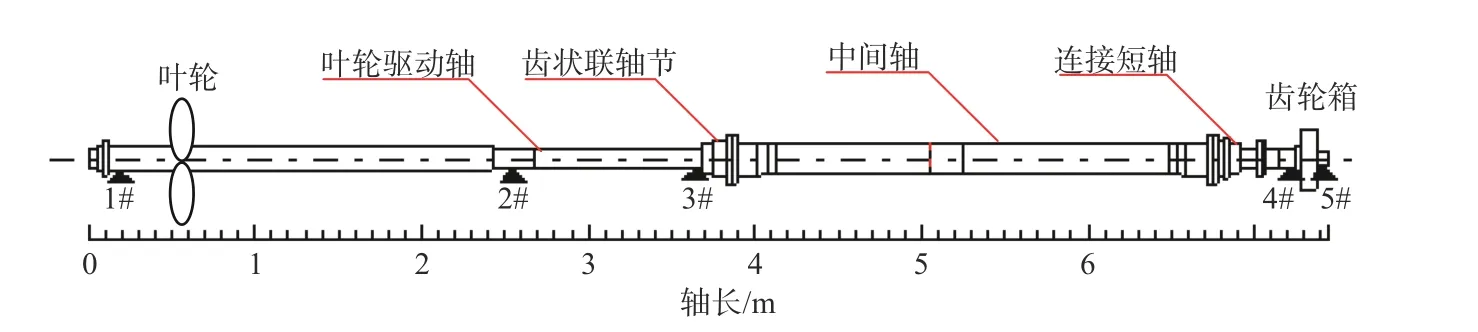
图 1 喷水推进轴系布置图Fig. 1 Diagram of waterjet propulsion shafting arrangement

轴系的工作原理简述如下：主机通过齿轮箱带动叶轮轴转动，叶轮将水流从船底吸入，并将水流增压增速，然后通过喷口收缩，向船体后方高速喷出水流。即利用水流动量变化产生的轴向力，通过叶轮轴传递至推力轴承座，再传递至船体，从而推动船舶前进。

根据船舶推进轴系回旋振动的计算方法，将喷水推进轴系简化为集总参数元件—分布参数元件的混合系统：叶轮按均质圆盘处理，考虑其陀螺效应，并将其考虑附水影响之后的质量和转动惯量作为集总参数加载到叶轮几何中心处；将叶轮驱动轴、中间轴等轴段进行自然分段，得到等截面匀质轴段元件，并将轴段元件进行细分；轴承按单点支承处理，支承点均取在轴承中点位置，并假定支承刚度各向相同；轴系首、尾两端边界条件均设为自由端。

为建立适用于数值分析的有限元模型，需在ANSYS中选择合适的单元来模拟各个轴系元件。ANSYS中的Beam 188单元是三维两节点梁单元，且每个节点具有6个自由度：UX（轴向位移）、UY（横向位移）、UZ（垂向位移）、ROTX（绕轴向转动）、ROTY（绕横向转动）和ROTZ（绕垂向转动）。该单元基于Timosheko梁结构理论（变形后横截面保持平面且不发生扭曲），考虑了剪切变形的影响，适用于从细长到中等粗短的梁结构分析，并支持大转动、大应变等非线性分析，故本文选用Beam 188梁单元来模拟轴系轴段。ANSYS中的质量单元Mass 21是具有6个自由度（UX，UY，UZ，ROTX，ROTY，ROTZ）的点单元，可以在3个坐标轴方向指定不同的质量和转动惯量，故本文选用Mass 21质量单元来模拟叶轮。ANSYS中的线性弹簧单元Combin 14具有轴向拉压的能力，其轴向的弹簧—阻尼器可以表示单轴拉压（沿轴线）单元，每个节点上至多有3个自由度，即沿节点坐标系X，Y，Z方向平动，但不能考虑弯曲或扭转，故本文选用Combin 14线性弹簧单元来模拟轴承，并设定其对轴段存在Y和Z方向的弹性支撑。

ANSYS参数化设计语言（ANSYS parametric design language，APDL）是一种解释性语言，具有顺序、选择、循环及宏等结构。利用APDL可以将ANSYS命令组织起来，编写参数化的应用程序，从而实现有限元分析的全过程，即参数化的实体模型、网格划分与控制、材料定义、载荷和边界条件定义、分析控制和求解以及后处理。

本文将利用APDL编写ANSYS命令流，建立喷水推进轴系的有限元模型，具体建模流程如图2所示。

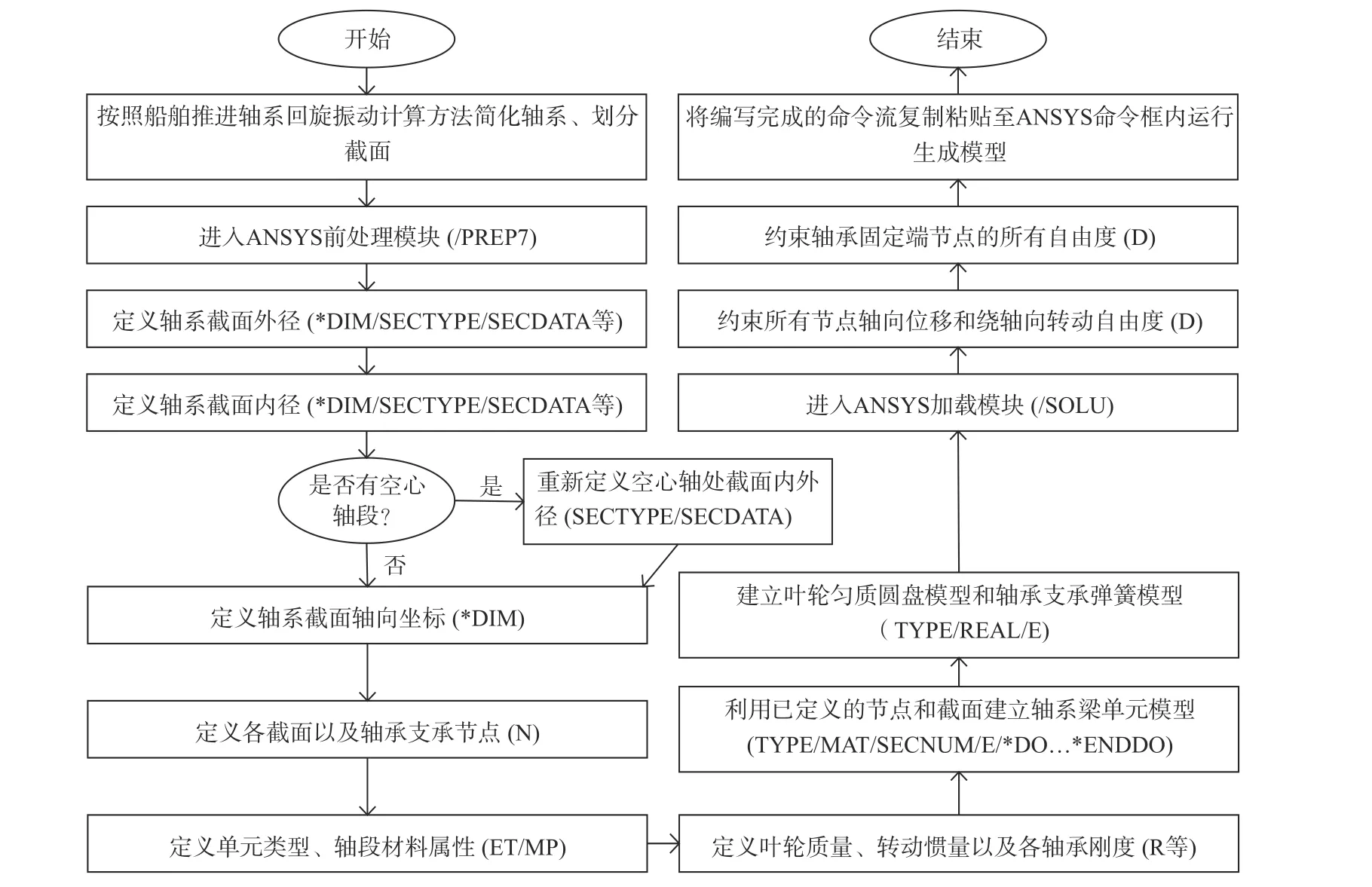
图 2 ANSYS命令流的建模流程图Fig. 2 Modeling flow chart of ANSYS command flow

1） 采用/PREP7命令进入ANSYS前处理模块，根据轴系简化和截面划分的结果，使用数组参数命令*DIM、截面形状命令SECTYPE、截面尺寸命令SECDATA以及循环命令*DO…*ENDDO，定义轴系截面内、外径和截面轴向坐标。然后，根据已经定义的截面轴向坐标，采用节点命令N定义各截面节点。

2） 根据各轴承支承截面轴向坐标，使用节点命令N定义各轴承支承节点；使用单元类型命令ET定义Beam 188梁单元、Mass 21质量单元和Combin 14线性弹簧单元；使用材料属性命令MP定义各轴段的材料属性，包括材料密度、弹性模量和泊松比；使用实常数命令R和单元关键项命令KEYOPT定义叶轮的质量和转动惯量、各轴承Y方向（横向）和Z方向（垂向）的刚度；使用单元号命令TYPE、材料号命令MAT、截面类型号命令SECNUM、节点号命令E及循环命令*DO…*ENDDO，建立轴系轴段梁单元模型；使用单元号命令TYPE、实常数命令REAL及节点号命令E，建立叶轮的匀质圆盘模型和各支承轴承的支承弹簧模型。

3） 采用/SOLU命令进入ANSYS加载模块，使用约束命令D约束所有节点的轴向位移自由度（UX）、绕轴向转动自由度（ROTX）以及轴承固定端节点的所有自由度（UX，UY，UZ）。

将编写完成的命令流复制粘贴至ANSYS命令输入框内，即可生成轴系有限元模型，如图3所示。该轴系模型共有65个节点，具体包括10个轴承支承节点、54个截面和1个点质量。

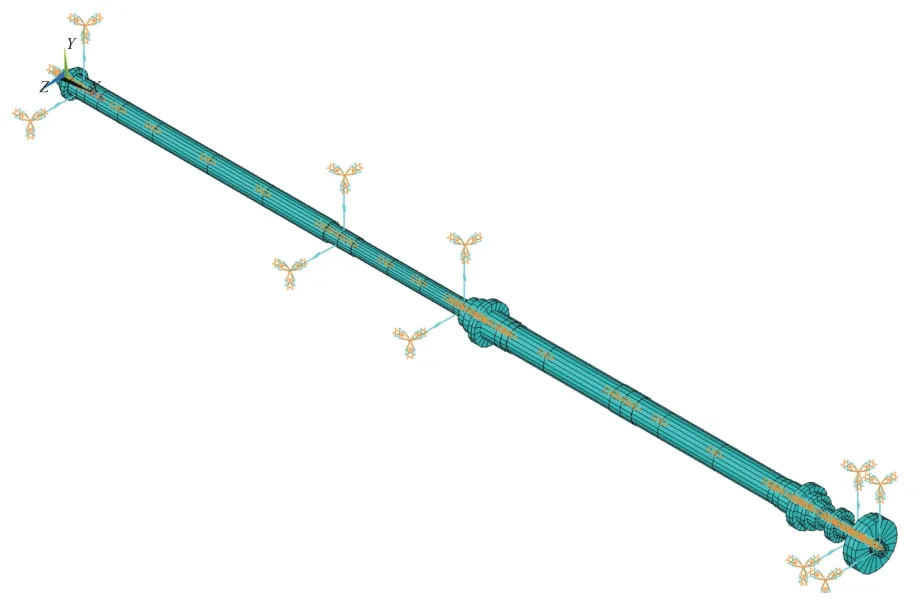
图 3 喷水推进轴系的有限元模型Fig. 3 Finite element model of waterjet propulsion shafting

2 喷水推进轴系回旋振动计算分析

2.1 轴系回旋振动

轴系回旋振动的实质是轴系进动，即轴系一方面绕其自身的几何中心线旋转，而另一方面弯曲的几何中心线又围绕支承中心线旋转[3]。轴系的回旋振动通常被视为横向振动，但二者在物理概念上有所区别：回旋振动属于旋转转子的涡动，而横向振动属于不旋转转子的固有振动，所以这是2种不同性质的物理现象[11]。轴系在运转过程中，由于陀螺效应的影响，其固有频率将随着转速的变化而变化。因此，为了更契合实际工程应用，在计算轴系回旋振动时应考虑陀螺效应，且一般仅需计算轴系一阶一次和叶片次正逆回旋的固有频率及临界转速。

2.2 基于ANSYS的坎贝尔图

在ANSYS中建立喷水推进轴系的有限元模型之后，即可利用ANSYS命令流得出喷水推进轴系的坎贝尔图。首先，使用/SOLU命令进入ANSYS加载求解模块，使用CORIOLIS命令考虑回转效应和转动阻尼效应，并使用求解类型命令ANTYPE定义求解类型为模态分析；然后，根据轴系额定转速设定转速间隔，使用旋转速度获取命令OMEGA定义转轴绕固定坐标系的转速，并采用循环命令*DO…*ENDDO控制轴系的转速，从而实现轴系在不同角速度下的多载荷步模态分析，并获得轴系的一阶固有频率及振动振型，图4所示为喷水推进轴系的第1阶振型图；最后，基于多载荷步模态的分析结果，使用/POST1命令进入ANSYS后处理模块，并使用坎贝尔图绘制命令PLCAMP和坎贝尔图打印命令PRCAMP得到旋转轴系的坎贝尔图，如图5所示。

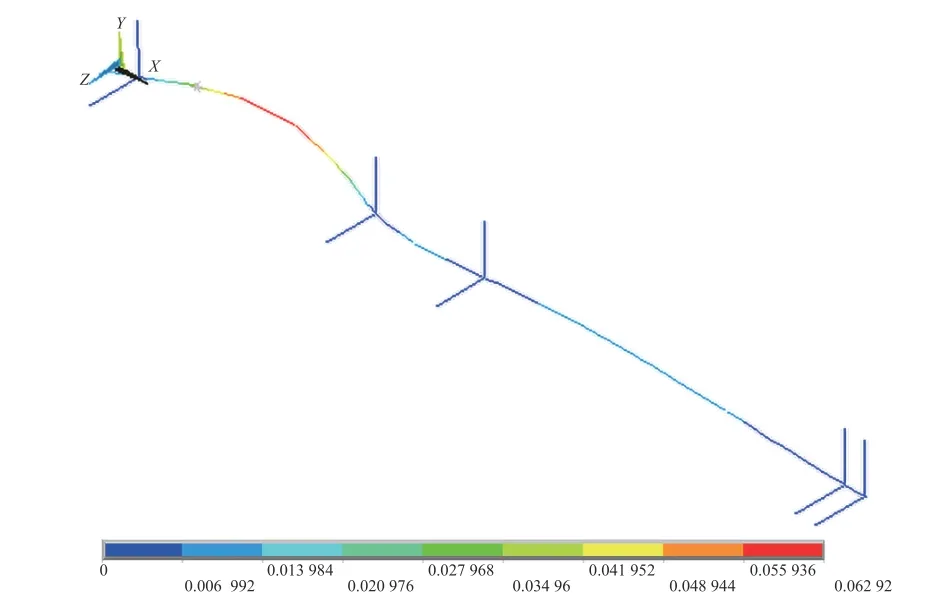
图 4 喷水推进轴系的第1阶振型图Fig. 4 First-order mode diagram of waterjet propulsion shafting

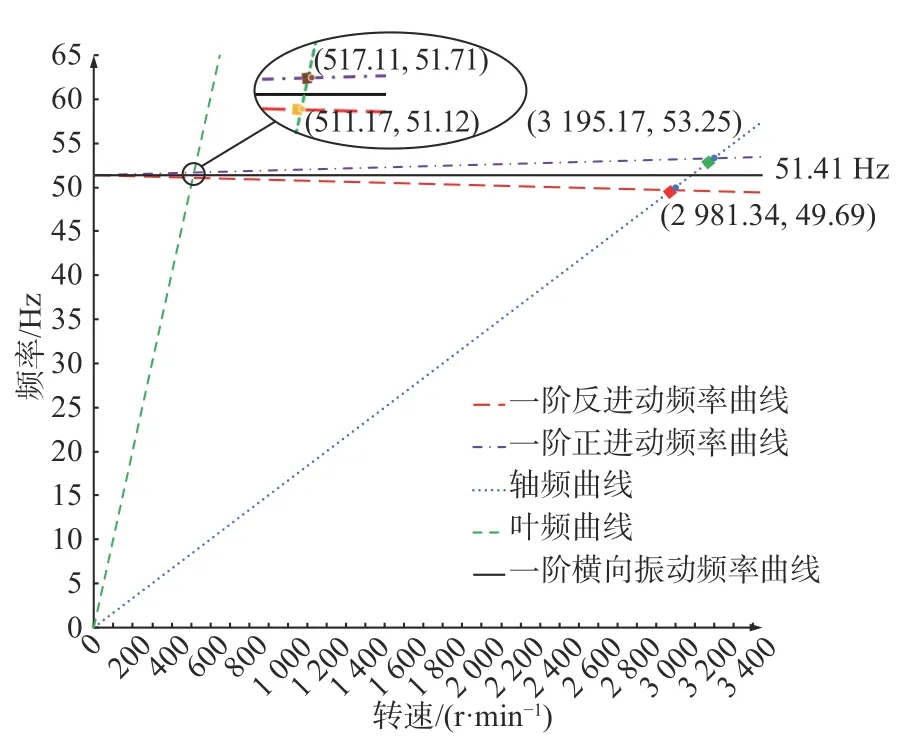
图 5 喷水推进轴系的坎贝尔图Fig. 5 Campbell diagram of waterjet propulsion shafting

基于坎贝尔图中轴系进动频率曲线与轴频、叶频曲线的交点，即可得到轴系一阶一次和叶片次正逆回旋的固有频率及临界转速，具体数值如表1所示。

2.3 结果分析

由轴系的第1阶振型图可知，喷水推进轴系的一阶弯曲模态频率为51.41 Hz，高于轴系的工作频率，且一阶模态位移的最大值位于叶轮轴之上。由轴系的坎贝尔图可知，当轴系转速为0时，一阶正进动频率曲线、一阶反进动频率曲线与一阶横向振动频率曲线相交于同一点，这是由于轴系的各轴承支承刚度设定为各向相同所致；如果各轴承支承刚度设定为各向不相同，则3条曲线不会相交于同一点。随着轴系转速的升高，其陀螺力矩也将随之增加，由坎贝尔图可知：在正陀螺力矩作用下，轴系的一阶正进动频率不断增加，并逐渐偏离一阶横向振动频率；在负陀螺力矩作用下，轴系的一阶反进动频率不断减小，并逐渐偏离一阶横向振动频率。

喷水推进轴系的一阶一次正回旋临界转速为3 195.17 r/min，一阶一次逆回旋临界转速为2 981.34 r/min，其偏差为7.1%；一阶叶片次正回旋临界转速为517.11 r/min，一阶叶片次逆回旋临界转速为511.17 r/min，其偏差为1.2%。由此可见，陀螺效应对一阶一次回旋临界转速的影响较大。

由上文可知，喷水推进轴系的额定转速为867 r/min，故其一阶一次正回旋临界转速为额定转速的368.5%，一阶叶片次正回旋临界转速为额定转速的59.6%，满足回旋振动临界转速的相关标准规定。

经计算得到一阶一次和叶片次正逆回旋临界转速之后，即可利用ANSYS命令流绘制一阶一次和叶片次正逆回旋临界转速下的喷水推进轴系涡动轨迹图，其具体命令如下：首先，使用/PREP7命令进入ANSYS前处理模块，使用数组参数命令*DIM定义一阶一次和叶片次正逆回旋临界转速的数组；然后，利用上文提到的求解方法，进入ANSYS加载求解模块，对轴系进行一阶一次和叶片次正逆回旋临界转速下的多载荷步模态分析；最后，使用/POST1命令进入ANSYS后处理模块，使用结果读取命令set和绘制模态轨迹命令plorb绘制一阶一次和叶片次正逆回旋的涡动轨迹图，其结果如图6～图9所示。

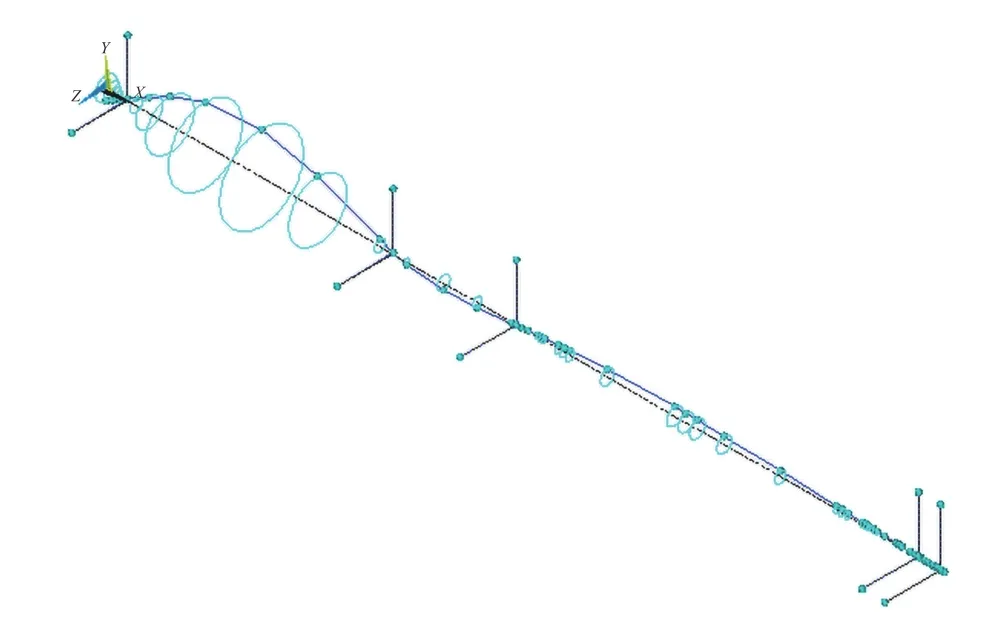
图 6 一阶一次正回旋涡动轨迹Fig. 6 Vortex trajectory of the first order positive whirling vibration

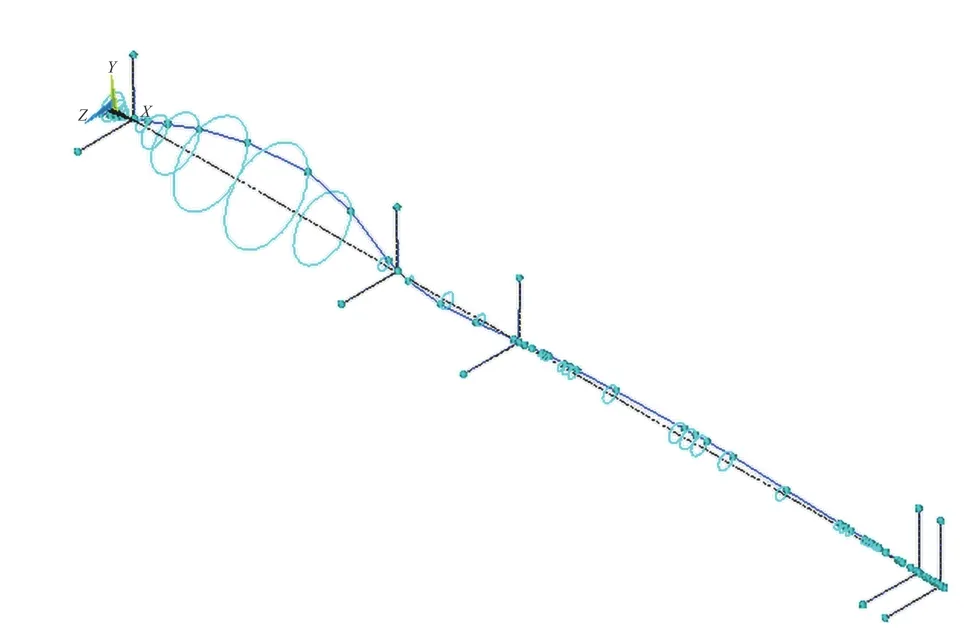
图 7 一阶一次逆回旋涡动轨迹Fig. 7 Vortex trajectory of the first order reverse whirling vibration

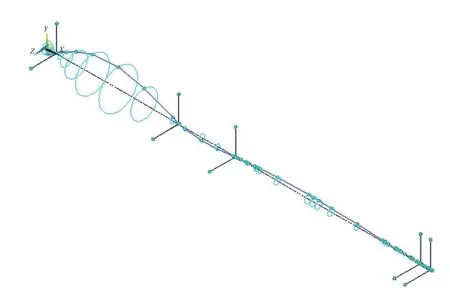
图 8 叶片次正回旋涡动轨迹Fig. 8 Vortex trajectory of the blade positive whirling vibration

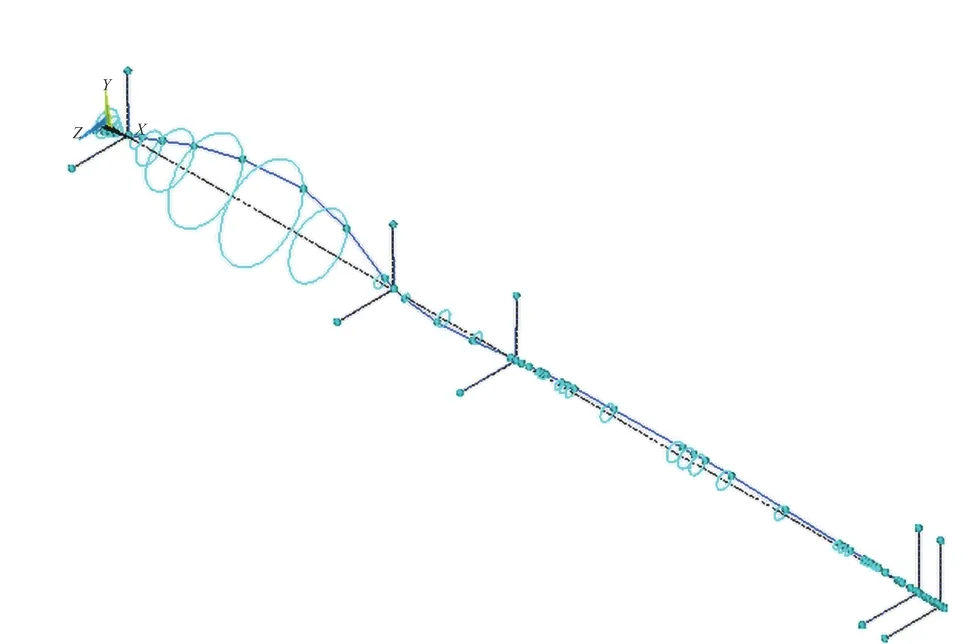
图 9 叶片次逆回旋涡动轨迹Fig. 9 Vortex trajectory of the blade reverse whirling vibration

涡动轨迹图描述了喷水推进轴系在一阶一次和叶片次正逆回旋临界转速下的涡动轨迹特征，从而直观展示了喷水推进轴系的回旋振动特性。由涡动轨迹图可知：喷水推进轴系叶轮驱动轴的回旋振动位移幅值最大，而中间轴和齿轮箱输出轴的回旋振动位移幅值则很小，可见叶轮的陀螺效应对叶轮驱动轴的影响较大，而对中间轴和齿轮箱输出轴的影响则较小，这一点在设计叶轮及艉部轴承支承时需谨慎考虑。

3 喷水推进轴系回旋振动的影响因素

影响轴系回旋振动的外部因素很多，例如外部激振力、轴系校中状态、轴承支承磨损、轴承布置方案及支承刚度等[12]，计算结果和实践经验表明，这些因素大多对轴系回旋振动存在一定的影响。本节将根据喷水推进轴系的布置方案，分别计算推力轴承不同的轴向布置位置和各支承轴承不同支承刚度下的回旋振动情况，进而分析其对喷水推进轴系回旋振动的影响。

3.1 推力轴承位置对回旋振动的影响

内置式喷水推进轴系的推力轴承有2种轴向布置方式：一是传统式轴系，即将推力轴承布置于叶轮轴的密封前端；二是分体式轴系，即将推力轴承布置于推进泵内部[10]。本文将分别计算这2种方案下的回旋振动情况。图10所示为推力轴承在不同轴向位置的轴系坎贝尔图。

基于坎贝尔图，即可计算推力轴承位置变化前后喷水推进轴系的一阶一次和叶片次正逆回旋临界转速与固有频率，其结果如表2所示。

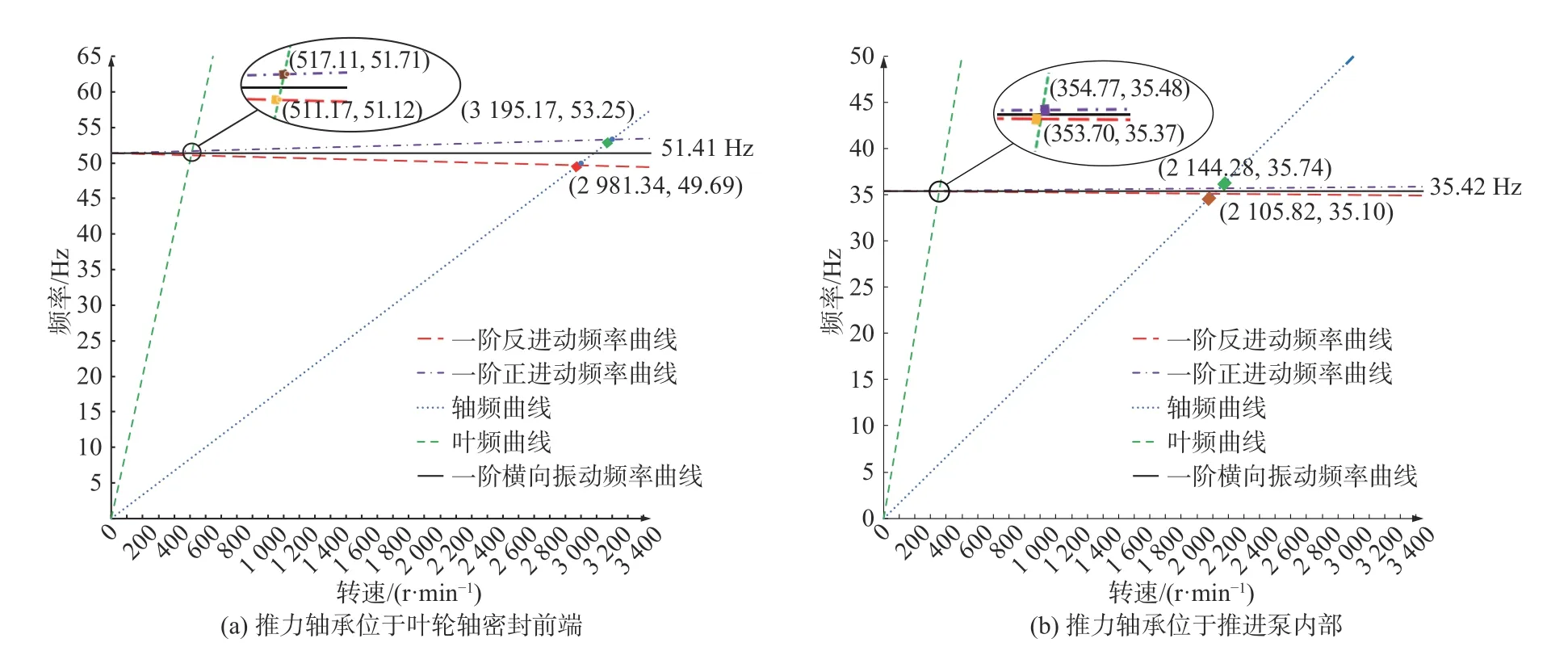
图 10 推力轴承不同轴向位置的坎贝尔图Fig. 10 Campbell diagrams of thrust bearing in different axial positions

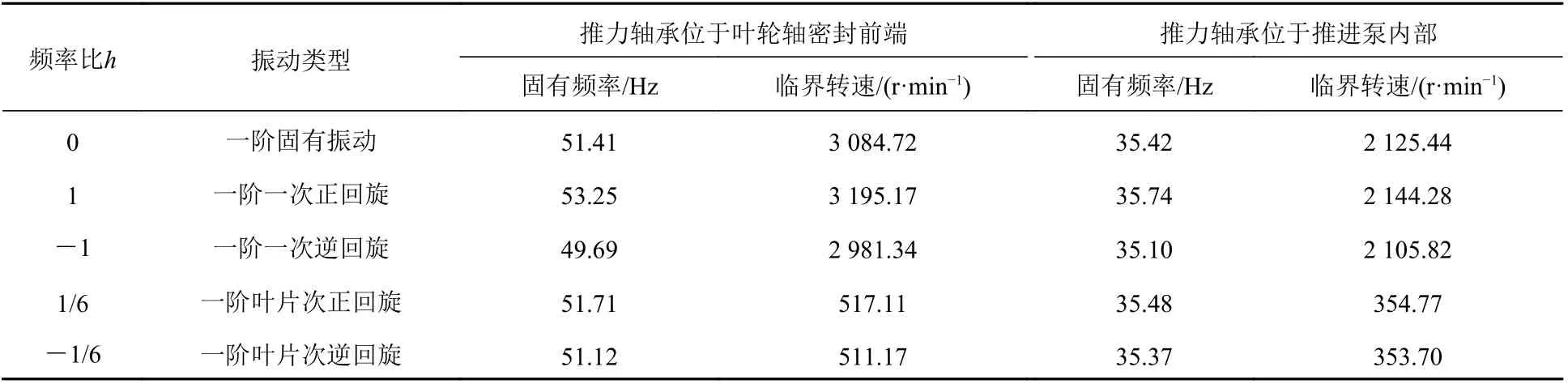
表 2 推力轴承不同轴向位置的固有频率和临界转速Table 2 Natural frequency and critical speed of thrust bearing with different axial positions

当推力轴承从艉密封前端移至推进泵内部时，相当于降低了轴的弯曲刚度，所以轴系的固有频率和临界转速也会随之降低。由表2可知：轴系的一阶一次正回旋临界转速下降了约32.8%；其一阶叶片次正回旋临界转速为354.77，约下降了31.3%。由此可见，内置式喷水推进轴系推力轴承的轴向布置方式对其回旋振动固有特性的影响很大，所以在设计阶段需慎重考虑。

3.2 轴承的支承刚度对回旋振动的影响

轴承的支承刚度是轴系回旋振动传递的重要影响因素，其不仅影响各处轴承力的分配，也将影响轴系固有频率和回旋响应特性的变化情况。轴承的支承刚度与很多参数有关，一般难以进行直接计算。根据实船数据，轴承支承刚度一般为2×108～10×109N/m。为了分析轴承支承刚度对喷水推进轴系回旋振动的影响，本文将计算轴承支承刚度从2×108N/m逐渐增加至10×109N/m的回旋振动情况。图11所示为喷水推进轴系在不同支承刚度下的坎贝尔图。根据坎贝尔图，即可计算轴承支承刚度变化前后轴系回旋振动的临界转速，结果如表3所示。

由表3可以看出，随着轴承支承刚度的增加，喷水推进轴系回旋振动的临界转速也随之增加。

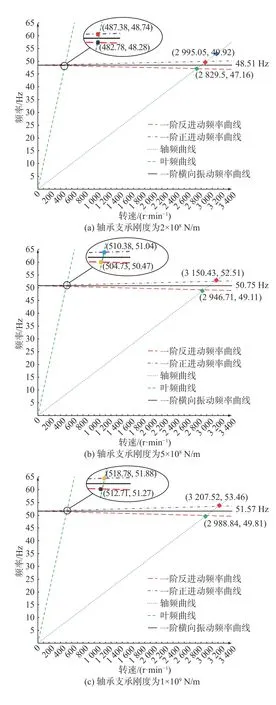
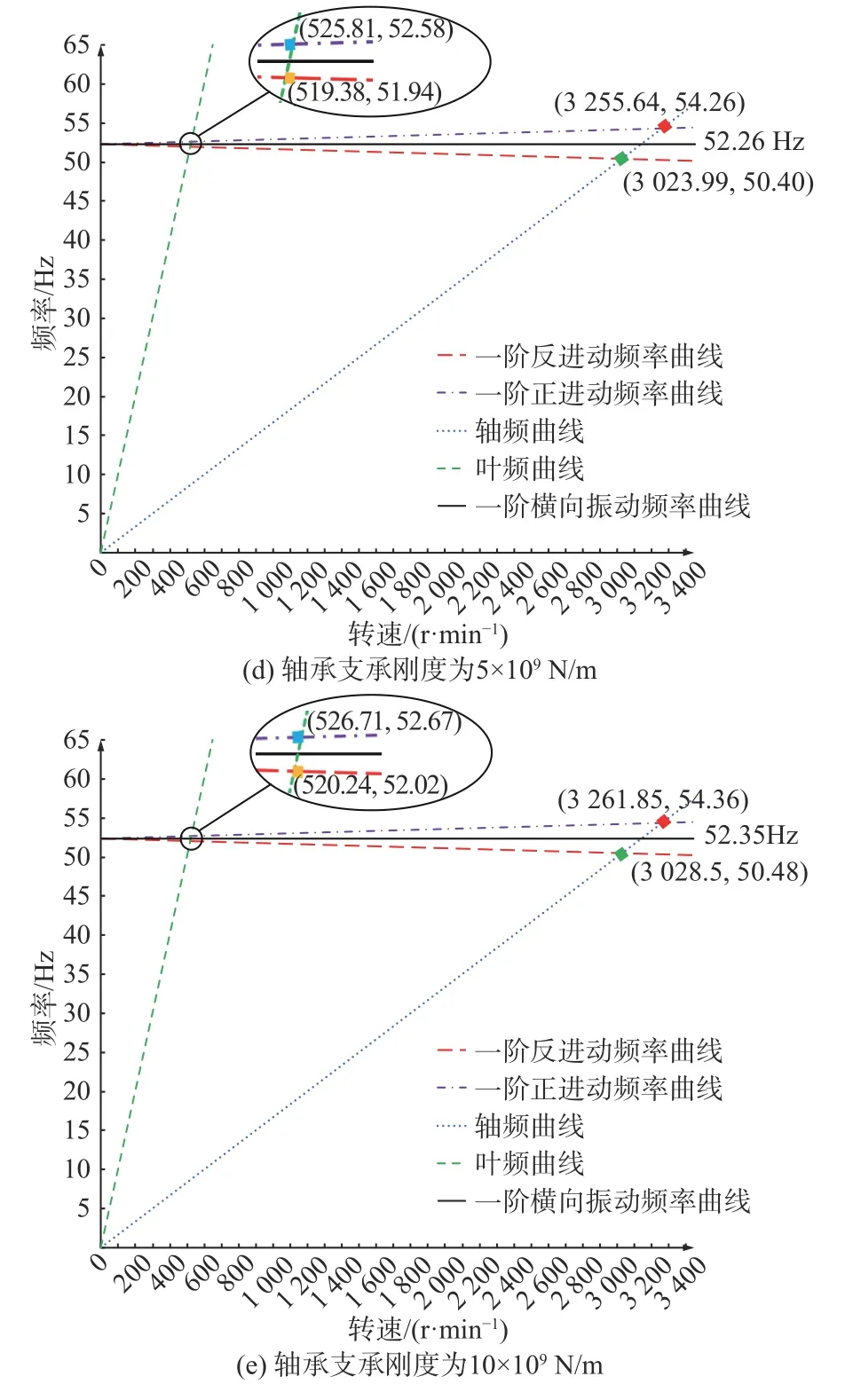
图 11 不同支承刚度下的坎贝尔图Fig. 11 Campbell diagrams under different bearing stiffness

轴系一阶共振转速的范围是2 910.42～3 140.70 r/min，变化幅度不超过8%；一次正回旋临界转速的范围是2 995.05～3 261.85 r/min，变化幅度不超过9%；叶片次正回旋临界转速的范围是487.38～526.71 r/min，变化幅度不超过8%。由此可见，轴承支承刚度对喷水推进轴系回旋振动临界转速的影响处于非敏感区，即使刚度略有变化，临界转速也不会发生明显变化，所以有利于轴系的工作转速避开临界转速，从而保证喷水推进轴系安全稳定运行。

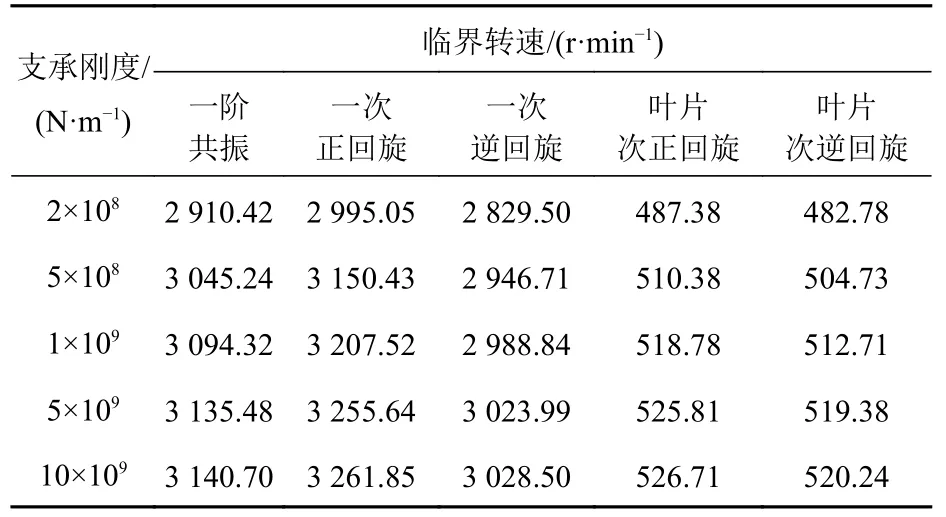
表 3 不同支承刚度下的回旋振动临界转速Table 3 Critical speed of whirling vibration under different bearing stiffness

4 结 论

本文以某40 m双体船喷水推进轴系为研究对象，利用ANSYS命令流提出了基于有限元法计算喷水推进轴系回旋振动的完整方法：首先，基于ANSYS命令流建立了喷水推进轴系的参数化有限元模型；然后，基于多载荷步模态分析和坎贝尔图计算了轴系的回旋振动情况；最后，分析了推力轴承的布置方式和各轴承的支承刚度对喷水推进轴系回旋振动的影响。经分析，该喷水推进轴系的回旋振动满足规范要求，验证了本文计算方法的可行性，结论如下：

1） 喷水推进轴系叶轮轴的回旋振动位移幅值较大，在设计叶轮轴及艉部支承时应慎重考虑。

2） 推力轴承的2种轴向布置方式对喷水推进轴系回旋振动的影响较大。

3） 轴承支承刚度对喷水推进轴系回旋振动临界转速的影响处于非敏感区，所以轴系存在一个相对稳定的临界转速，这将有利于轴系的安全平稳运行。