基于高阶矩法的CRTSⅡ型轨道板抗裂可靠度*
张龙文, 周劲
(1.湖南农业大学水利与土木工程学院,湖南 长沙 410128; 2.中南大学土木工程学院,湖南 长沙 410076)
截至2018年底,中国高铁的运营里程接近3万公里,位居世界第一。无砟轨道结构因具有稳定性高、耐久性好、维修工作量少等优点,在我国高速铁路上获得越来越广泛的应用[1-2]。无砟轨道结构类型有CRTS Ⅰ型板式、CRTS Ⅱ型板式、CRTS Ⅲ型板式、CRTS Ⅰ型双块式以及CRTS Ⅱ型双块式无砟轨道。其中CRTS Ⅱ型板式无砟轨道结构是我国目前铺设里程最长的轨道结构形式,广泛应用于我国京津、京沪、沪昆等多条客运专线中。
目前,对于CRTS Ⅱ型轨道板的设计主要采用容许应力方法。容许应力法已不能完全适应新形势下结构设计的需要,采用基于可靠度理论的极限状态设计方法已经成为国际主流趋势。近几年来,可靠度理论已经逐步应用于CRTS Ⅱ型板式无砟轨道结构设计。其中,CRTS Ⅱ型板式无砟轨道结构的抗裂可靠度为重点研究问题之一。对CRTS Ⅱ型板式无砟轨道结构进行分析时,列车竖向荷载效应计算往往需要通过有限元方法进行分析,难以建立显式功能函数,给可靠度分析带来困难。针对该问题,许多学者对CRTS Ⅱ型板式无砟轨道结构抗裂可靠度方面进行了相关的研究。例如,张国虎[3]采用有限元与蒙特卡罗相结合的方法,通过ANSYS有限元软件中的可靠性分析模块(PDS)对CRTS Ⅱ型板式无砟轨道结构进行可靠度分析,但其需要进行成千上万次的有限元模拟,工作量大,不适用于实际工程;李怀龙等[4]假设轨道板为“串联宽轨枕”,采用弹性地基梁模型建立了列车荷载效应的显式表达式,并用一次二阶矩法[5]进行可靠度计算,该方法避免了隐式函数计算问题,但是一次二阶矩方法对于实际工程中的强非线性问题,多验算点问题等都难以发挥效力。针对一次二阶矩存在的问题,众多学者发展了多种结构可靠度分析方法,如二次二阶矩法[6-7],响应面法[8-9]等,这些方法虽然在一定程度上解决了验算点法的某些弱点,但却使得结构可靠度分析越来越复杂。近年来,赵衍刚等和卢朝辉等[10-11]直接通过功能函数的高阶矩(均值、标准差、偏度、峰度)来计算破坏概率,发展了一个以高阶矩法为基础的结构可靠度理论体系。该方法计算简单,用前四阶矩代替功能函数分布,简单有效地解决了一次二阶矩法迭代验算问题,从而为CRTS Ⅱ型板式无砟轨道结构可靠度分析提供了新途径。
基于此,本文利用ANSYS软件建立CRTS Ⅱ型板式无砟轨道结构有限元模型,针对隐式功能函数问题,提出点估计-有限元的前四阶矩计算方法,进而发展了基于高阶矩可靠度理论的CRTS Ⅱ型板式无砟轨道结构抗裂可靠度分析方法。最后,通过实例分析,说明了本文方法的应用,验证了本文提出方法的高效性与精确性。
1 CRTS Ⅱ型轨道板抗裂功能函数
1.1 列车荷载与温度共同作用下的轨道板抗裂功能函数
CRTS Ⅱ型轨道板的设计思路之一是轨道板在使用过程中假缝允许开裂成为“真缝”,轨道板从铺设时的“板”转变为采用纵连钢筋串联的“宽轨枕”。因此,对于轨道板横向按预应力混凝土轨枕设计,即列车荷载和梯度温度的共同作用下不出现裂缝,CRTS Ⅱ型轨道板抗裂功能函数Z表达为[12-13]
(1)
式中,MR为截面开裂弯矩;ML1为列车竖向荷载作用下引起的弯矩;ML2为列车横向荷载作用下引起的弯矩;MT为梯度温度作用下引起的弯矩;γR为抗力分项系数,取值为1.4;γ0为结构重要系数,取值为1.0;Tw为结构计算模型不确定系数;γL为列车荷载分项系数,取值为1.5;φT为组合系数,取值为0.5;γT为梯度温度作用分项系数,取值为1.0。
式(1)中列车横向荷载作用下的弯矩ML2,表达为[14]
ML2=0.3Q·h
(2)
式中,h为轨道板至轨面的距离;Q为列车横向荷载,取竖向列车荷载的0.8倍。
CRTS Ⅱ型轨道板由于宽度较宽,板的上下表面将承受梯度温度作用。为方便计算,对于无砟轨道翘曲应力,不管是单元式还是连续式轨道,其上层轨道板的纵、横向翘曲应力,均按完全约束无限大板的Westgaard翘曲应力公式计算。在梯度温度作用下轨道板弯矩MT表达为[14]
(3)
式中,Ecν,α分别为轨道板混凝土材料的弹性模量、泊松比及线膨胀系数;Tg为温度梯度;h为轨道板厚度;αh为温度梯度板厚修正系数,取1.05。
1.2 列车竖向荷载作用下的轨道板有限元模型及其弯矩
利用ANSYS有限元软件建立弹性地基上的CRTS Ⅱ型板式无砟轨道梁板模型进行列车竖向荷载作用下的弯矩ML1计算。钢轨简化为弹性点支承梁,采用BEAM188单元模拟;轨道板和底座板采用板壳单元SHELL63模拟;扣件、CA砂浆填充层采用弹簧单元COMBIN14模拟;参考文献[14],下部基础采用弹性地基模型。为了考虑扣件的尺寸效应,将每个钢轨节点与其对应的扣件尺寸范围内(150 mm×300 mm)的轨道板节点均相连,计算模型如图1所示。
模型中钢轨采用CHN60钢轨,弹性模量为2.1×105MPa,泊松比为0.3;扣件选用WJ-8型扣件,扣件节点的垂直静刚度为40 kN/mm,间距0.65 m;轨道板采用实际尺寸,宽度为2.55 m,厚度为0.2 m,采用C55混凝土,弹性模量为3.55×105MPa,泊松比为0.2。为了消除边界的影响,取等效3块轨道板的长度为19.45 m考虑;CA砂浆其长度、宽度与轨道板相同,采用离散弹簧来模拟,弹性模量取7 000 MPa;底座板宽度为2.95 m,厚度为0.2 m,采用C30混凝土,弹性模量为3.0×105MPa;地基系数取1 000 MPa/m。
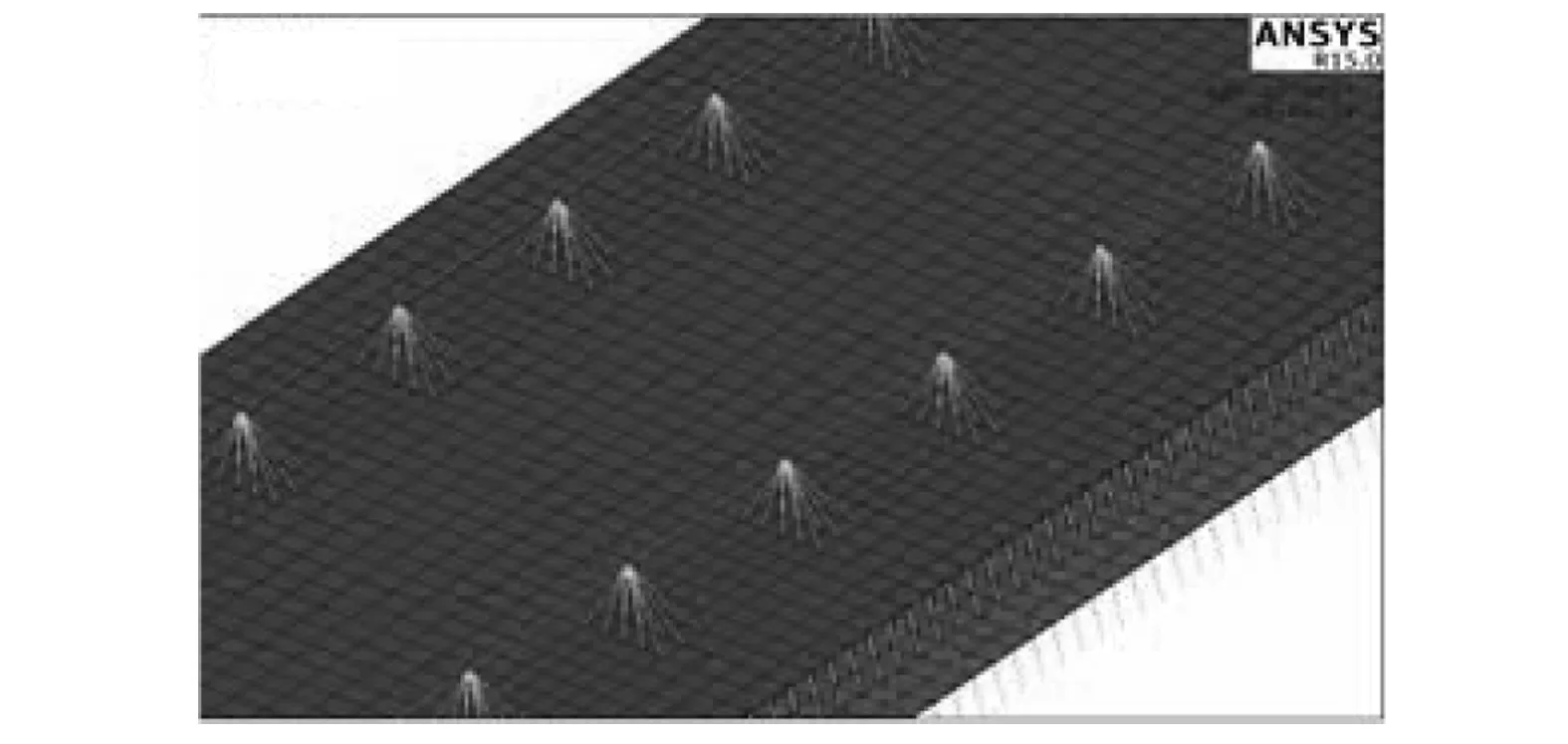
图1 CRTS Ⅱ 型板式无砟轨道力学模型Fig.1 Mechanical model of CRTS Ⅱ slab ballastless track
根据上述建立的列车竖向荷载作用下的轨道板有限元模型,设列车竖向荷载作用下的轨道板弯矩ML1的所有随机变量组成的基本随机变量X=[x1,x2,…,xn]T,则ML1表示为X的隐式函数:
ML1=S(X)=S(x1,x2,…,xn)
(4)
2 高阶矩可靠度分析方法
2.1 功能函数的前四阶矩
一般地,对于功能函数Z=G(X),向量X=(x1,x2,…,xn)代表n个基本随机变量,前四阶矩根据定义表达为
(5a)
(5b)
(5c)
式中,μG、σG分别为功能函数Z=G(X)的均值和标准差;αkG(k=3,4)分别为功能函数Z=G(X)的偏度(k=3)与峰度(k=4);fx(X)是基本随机变量X的联合概率密度函数。对于一些简单的功能函数,如随机变量较少的线性函数或独立随机变量的乘积,其各阶矩可直接由上述积分得到。然而在实际工程中,存在功能函数的维数高甚至是隐式表达式等情况,直接积分计算非常复杂,因此利用减维方法简化计算十分必要。
2.2 多随机变量功能函数前四阶矩的二维减维点估计方法
对于功能函数Z=G(X),运用Rosenblatt逆变换,则功能函数的第k阶原点矩[15]表达为
(6)
式中,T-1(u)为Rosenblatt逆变换,φ(u)为标准正态随机变量的概率密度函数,u=(u1,u2,…,un)代表n个标准正态分布的随机变量。设式中的{G[T-1(u)]}为L(u),表达为[16]
(7a)
式中
L0=L(0,…,0,…,0)
(7b)
(7c)
(7d)
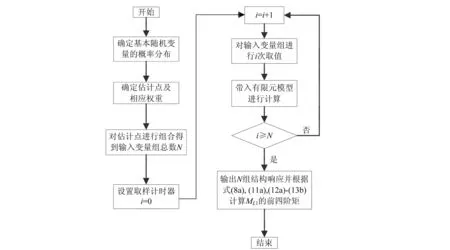
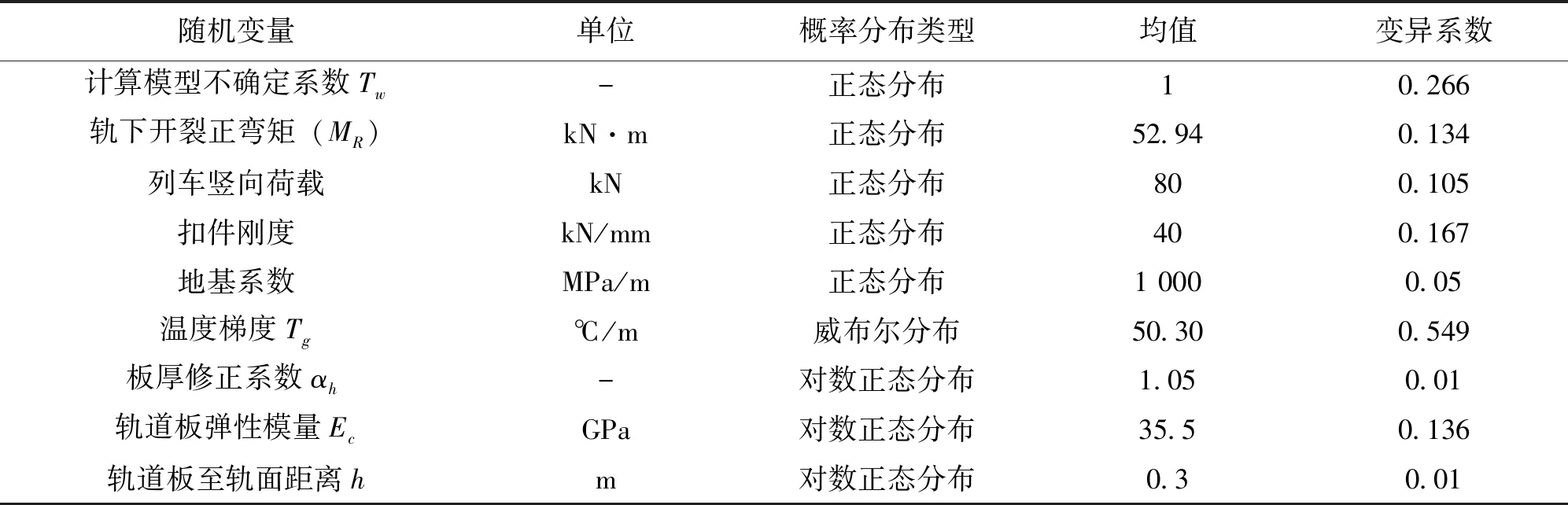
式中,i,j=1,2,…,n,且i 将式(7a)-(7d)带入式(6),则n维函数的积分简化为二维函数之和的积分计算,式(6)进一步表达为 (8a) (8b) (8c) (8d) 利用Gauss-Hermite积分公式,式(8b)和(8c)可分别近似表示为: (9a) (9b) 式中,uiq,ujr指标准空间估计点,Piq,Pjr指标准空间估计点相应的权重。若采用标准正态空间中的7点估计即m=7,则估计点值uiq(q=1,2m)及权重Piq,或ujr(r=1,2m)及权重Pjr如下式所示[16]: ui1=uj1=-3.750 439 7,Pi1=Pj1=5.482 69×10-4 (10a) ui2=uj2=-2.366 759 4,Pi2=Pj2=3.075 71×10-2 (10b) ui3=uj3=-1.154 405 4,Pi3=Pj3=0.240 123 3 (10c) ui4=uj4=0,Pi4=Pj4=0.457 142 7 (10d) ui5=uj5=1.154 405 4,Pi5=Pj5=0.240 123 3 (10e) ui6=uj6=2.366 759 4,Pi6=Pj6=3.075 71×10-2 (10f) ui7=uj7=3.750 439 7,Pi7=Pj7=5.482 69×10-4 (10g) 为便于理解与计算,将式(7b)-(7d),及(9a)-(9b)转化至原始空间,表达为 L0=Gμ(μ1,…,μi,…,μn) (11a) (11b) (11c) 式中,μ1(1,2,…,n)指第i个基本随机变量的均值,xi(xj)指第i(j)个基本随机变量的原始空间估计点。 (12a) (12b) 将式(11a), (12a)-(12b)代入式(8a)计算μkG,k值取1-4,即功能函数的前四阶原点矩。根据原点矩与中心矩的关系,含n个基本随机变量的功能函数G(X)的前四阶矩(即均值μG、标准差σG、偏度α3G和峰度α4G)表达为 (13a) (13b) 不失一般性,功能函数Z=G可以等效转化为均值为零和标准差为1的标准化功能函数ZG,即: (14) 式中,ZG可以近似表示为标准正态随机变量u的一元三次多项式即四阶矩标准化函数[11]。 ZG=S(u,M)=-l1+k1u+l1u2+k2u3 (15) 式中,M为功能函数Z=G的前四阶矩(μG,σG,α3G, α4G)向量,l1,k1,k2为多项式系数。 (16) 其中,l2为 (17) 根据式(15),四阶矩标准化函数的逆函数S-1表达为 (18) 式中, (19) 根据失效概率的定义,功能函数Z=G对应的失效概率Pf可以表示为 (20) 假设ZG的概率分布函数CDF为F(ZG),则根据等概率变换 F(ZG)=Φ(u)=Φ[S-1(ZG,M)] (21) 式中,Φ(u)为标准正态随机变量的累积分布函数;S-1(ZG,M)为式(15)的逆函数。 接着,式(20)可以进一步表达为 Pf=F(-β2M)=Φ[S-1(-β2M,M)] (22) 根据可靠指标与失效概率的关系及式(22),四阶矩可靠指标表达为[11] (23) 式中, (24) 为了计算列车竖向荷载作用下轨道板弯矩的前四阶矩,基于1.2节建立的轨道板有限元模型,本文提出了点估计-有限元法,具体实施步骤如下: (1) 建立CRTS Ⅱ型轨道板的有限元分析模型; (2) 确定影响列车竖向荷载作用下的轨道板弯矩的基本随机变量X的分布类型和统计参数; (3) 确定估计点个数m以及标准空间中的估计点及相应权重,进而通过Rosenblatt逆变换得到原始空间中的估计点; (4) 对n个基本随机变量在原始空间的估计点进行组合,组合方法如下: ① 基本随机变量X均在均值点取值,即一组输入变量Xμ=[μ1,μ2,…,μn]T;记为输入变量第一部分。 ② 基本随机变量X中任意一个变量取m个估计点,其余基本随机变量均取均值,即得到C1n×m组输入变量Xi=[μ1,…,xi,r, …,μn]T,i=1,2,…,n;r=1, 2, …,m;记为输入变量第二部分。 (5) 将N组基本随机变量X的估计点依次带入有限元模型中进行轨道板弯矩确定性分析,进而输出N组列车竖向荷载作用下的轨道板响应值; (6) 将各组计算的响应值及其相应的权重,代入式(12a)-(12b),进而结合式(8a),(11a)及(13a)-(13b)计算列车竖向荷载作用下轨道板弯矩ML1的前四阶矩。 根据以上具体步骤,列车竖向荷载作用下的轨道板弯矩ML1的前四阶矩计算流程如图2所示。 图2 点估计-有限元方法计算前四阶矩流程图Fig.2 The flow chart of the first four moments calculated by point estimate-finite element method 文献[3]收集了24组轨道板静载试验数据,认为轨道板轨下开裂正弯矩(MR)服从均值为52.94 kN·m,标准差为7.09 kN·m的正态分布;文献[17]分析了CRTS Ⅱ型板式无砟轨道结构在列车竖向荷载作用下参数的敏感性,把列车竖向荷载、扣件刚度和地基系数视为随机变量;在分析梯度温度作用下的轨道板弯矩MT时,本文将温度梯度、板厚修正系数、轨道板弹性模量视为随机变量;分析列车横向荷载作用下轨道板弯矩ML2时,本文将列车竖向荷载和轨道板至轨面的距离视为随机变量;参考文献[3]与[17],基本随机变量的统计矩和分布类型如表1所示。 表1 CRTS Ⅱ型轨道板基本随机变量的统计矩与分布类型Table 1 Statistical moments and distribution types of basic random variables of CRTS Ⅱ track slab (25) 从图3可以看出,随着循环次数的增加,弯矩ML1的前四阶矩在Nsim=105时结果趋近收敛。因此,本文以Nsim=105时计算的前四阶矩作为准确值与本文方法计算结果进行对比。 表2 本文方法与随机有限元法计算的前四阶矩及其相对误差Table 2 The first four moments calculated by the proposed method and stochastic finite element method and its relative errors 图3 不同模拟次数的轨道板弯矩ML1的前四阶矩Fig.3 The first four moments of bending moment of track slab ML1 under different simulation times 表2给出了本文方法与随机有限元法Nsim=105时计算的前四阶矩及其相对误差。从表2可以看出,本文方法计算得到的轨道板弯矩ML1的前四阶矩与随机有限元法计算结果吻合,相对误差控制在5%之内,验证了本文方法的有效性。由于本文方法只需计算323次,而随机有限元法需计算105次,表明本文方法对于竖向荷载作用下轨道板弯矩前四阶矩计算即隐式函数前四阶矩的计算具有高效性。 4.2.2 其余基本变量的前四阶矩 从表1可知,轨下开裂弯矩MR及计算模型不确定系数Tw服从正态分布,根据正态分布的性质可知,该类变量的偏度和峰度分别为0与3。MR与Tw的标准差根据表1中均值与变异系数求得。MR与Tw的前四阶矩列于表3中。 当计算有显式表达式的列车横向荷载作用下轨道板弯矩ML2以及梯度温度作用下轨道板弯矩MT的前四阶矩时,根据式(5a)-(5c)的定义积分计算前四阶矩,列于表3中。 表3 随机变量及功能函数的前四阶矩Table 3 The first four moments of random variables and performance function 4.2.3 轨道板抗裂可靠指标 将各基本随机变量(MR,Tw,ML1,ML2,MT)分别看作功能函数G1,G2,G3,G4,G5,利用表2与表3中各随机变量(MR,Tw,ML1,ML2,MT)的前四阶矩,根据式(14)-(17)同时产生G1,G2,G3,G4,G5的随机样本,进而根据式(1)计算总体功能函数Z的样本即采用Monte-Carlo模拟方法对式(1)进行功能函数样本计算。类似地,根据统计矩的定义即式(25)计算总体功能函数Z的前四阶矩,如表3所示。最后,利用功能函数的前四阶矩,根据式(23)计算得到CRTS Ⅱ型轨道板的抗裂可靠指标为4.63。 参照《铁路工程结构可靠度设计统一标准》[18]中对工程结构安全等级的规定,CRTS Ⅱ型板式无砟轨道轨道板应按二级安全等级进行设计,其可靠指标应在3.2以上。因此,本文方法计算结果满足规范可靠指标要求。 (1) 提出了基于点估计-有限元计算隐式函数前四阶矩的计算方法。实例分析表明本文计算前四阶矩与随机有限元模拟(Monte-Carlo模拟)结果吻合,验证了本文方法的高效性与精确性,为CRTS Ⅱ轨道板结构在隐式功能函数情况下前四阶矩的计算提供了高效合理的工具。 (2) 发展了基于高阶矩理论的CRTS Ⅱ轨道板抗裂可靠度分析方法。通过实例计算得到CRTS Ⅱ 型轨道板抗裂可靠指标为4.63,满足《铁路工程结构可靠度设计统一标准》[18]的结构可靠指标要求。 (3) 本文仅考虑了CRTS Ⅱ轨道板抗裂可靠度,但本文方法可类推至处理隐式功能函数的轨道结构体系可靠度分析中,且对CRTS Ⅱ轨道结构设计理论及维修策略等有一定的理论参考价值和借鉴意义。2.3 四阶矩可靠指标
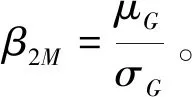
3 点估计-有限元方法计算前四阶矩步骤


4 算例分析
4.1 结构基本随机变量的统计矩和分布类型
4.2 功能函数的前四阶矩及可靠指标




5 结 论

