一种基于多尺度极值的快速自适应二维经验模式分解方法

杨 达，刘述田，徐冠雷，王晓炜

（1.大连东软信息学院智能与电子工程学院，大连，116023；2.海军大连舰艇学院军事海洋系，大连，116018；3.大连医科大学基础医学院，大连，116044）

引 言

经验模式分解[1]是近20年来发展起来的一种新型强大的自适应多分辨率信号时频处理方法，特别适用于非线性非平稳信号的分析处理，因此经验模式分解思想在一维、二维、多维和多变量信号处理方面得到持续的关注和深入的研究[2-5]。传统二维经验模式分解（Bidimensional empirical mode decomposition,BEMD）方法因其无需预定义任何基函数、完全数据驱动且信号分析能力强，在图像等二维信号的分析处理中体现出许多优势和巨大潜力[6-8]，然而BEMD方法在求解上下包络插值过程中非常耗时，并且由于离散点插值存在过冲和欠冲情况，使得分解出的分量中会存在比较明显的伪像[9-10]。2008年，Bhuiyan等提出了一种新的快速自适应二维经验模式分解方法，即FABEMD方法[11]。该方法利用统计排序平滑滤波代替了离散点插值，极大地提高了分解效率，改善了分解效果，显著地促进了二维经验模式分解方法在图像融合、图像增强、图像配准以及图像运动估计等领域的广泛应用[12-15]。文献[16-17]通过实验指出，基于BEMD和FABEMD的图像处理方法比对比度金字塔和小波变换等传统多尺度分解方法具有更好的效果。然而，包括FABEMD方法在内的现有二维经验模式分解算法在极值点查找、内蕴模式筛选以及迭代分解过程中效率比较低，自适应性依赖于一些参数的人工选择。如果对FABEMD方法进行改进，将能够进一步促进经验模式分解在图像处理领域的应用。

信号的多尺度极值点蕴含了存在于不同尺度上的丰富信息，成为近年来提高信号处理技术的一个研究方向。2013年，笔者提出了一维信号多尺度极值二叉树结构的概念，研究了其特性，并将其用于一维信号趋势项的快速提取[18-19]，为一维非线性非平稳信号的快速分析提供了一个新的思路。本文通过将一维多尺度极值二叉树概念推广到二维信号中，提出了一种高效的二维多尺度极值二叉树建立方法，并在此基础之上提出一个新的分解层数和滤波窗口大小的自适应确定原则，结合基于统计排序的平滑滤波方法实现了基于多尺度极值的二维信号经验模式分解方法(Improved fast and adaptive BEMD，IFABEMD)，从而显著提高了二维信号多尺度分解的自适应性及分解效率。

1 二维信号多尺度极值点集的二叉树结构及其生成方法

1.1 一维信号多尺度极值的二叉树结构

文献[18]提出了如图1所示的一维信号极值点的二叉树结构及其生成方法，具体过程总结如下：

（1）对于一个给定的一维多分量信号f(t)，其支撑为[0,T]，找出该信号所有的局部极大值点和极小值点，得到集合S〈1,1〉,S〈1,2〉，形成代表最小时间尺度的一级极值点集合S1={S〈1,1〉,S〈1,2〉}。

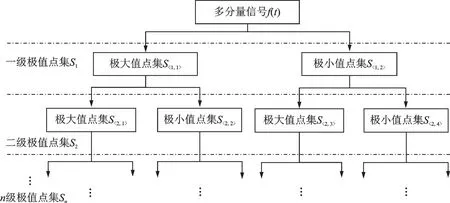
图1 信号极值点的二叉树结构Fig.1 Binary tree of multi-level signal extrema

（2）再分别将S〈1,1〉,S〈1,2〉作为新的序列分别找出它们的局部极大值点和极小值点，得到集合S〈2,1〉,S〈2,2〉，S〈2,3〉和S〈2,4〉，从而得到第二级极值点集S2={S〈2,1〉,S〈2,2〉，S〈2,3〉,S〈2,4〉}。

（3）依此类推，迭代上述操作，直到某一级极值点子集S〈i,j〉的元素数小于3停止迭代，此时的i等于n，被称为多尺度极值的最高级数，而上述迭代过程得到的各级极值点集合和子集就形成了如图1所示的一维信号极值点的二叉树结构。该二叉树结构的多尺度极值点集的获得，有助于对信号进行进一步的多尺度分析。

1.2 二维信号多尺度极值的二叉树结构

将一维多尺度极值二叉树概念推广到二维信号中可以得到：

（1）设I为一个多分量构成的二维信号，F为某种二维局部极值点查找操作，S为其多尺度极值点集合，Si为S的第i级子集。对I进行一次F操作，可以得到I的局部极大值点集S〈1,1〉和局部极小值点集S〈1,2〉，即：F(I)→(S〈1,1〉,S〈1,2〉)，由极值点集S〈1,1〉,S〈1,2〉形成第一级极值点子集S1，即S1={S〈1,1〉,S〈1,2〉}。

（2）再分别对S〈1,1〉,S〈1,2〉进行F操作，可以得到第二级极值点子集S2={S〈2,1〉,S〈2,2〉,S〈2,3〉,S〈2,4〉}，其中F(S〈1,1〉)→(S〈2,1〉,S〈2,2〉)，F(S〈1,2〉)→(S〈2,3〉,S〈2,4〉)。

（3）依此类推，每一个极值点集合又可进一步划分为下一级的两个极值点子集，即第i级（i=1，2，…，n，其中n为最高级极值点的级数）极值点集Si可划分为2i个极值点子集，因此，信号I的多级极值点集可表示为S[m]={Si}={S〈i,j〉},i=1,2,…,n;j=1,2,…,2i。其中，S〈i,j〉表示第i级极值点集中的第j个极值点子集。由此可建立二维信号极值点的二叉树结构，也可用图1表示。

1.3 基于一维多尺度极值点集的二维多尺度点集的生成方法

利用基于窗口的p-邻域比较法和基于Voronoi多边形的邻域比较法可以将二维信号局部极值点的查找直接推广到二维多级极值点。但前者窗口尺寸p的选择缺乏自适应性，无法反映出信号内在频率模式的信息，而后者是以8-邻域比较方法得到一级极值点；二级和二级以上的极值点由Voronoi多边形内节点与相邻多边形内节点比较得到，虽具有对信号自适应的特点，但随着极值点级数的增加，极值点数快速减少，很快出现极值点稀疏情况，不利于挖掘信号内部包含的众多频率模式分量。因此本文给出基于一维多尺度极值点集的二维多尺度点集的生成方法。二维多尺度极值点集的建立方法具体步骤如下：

（1）如图2所示将图像I分别沿水平方向和垂直方向蛇形展开，生成两个一维信号f1和f2。图中实心圆点代表一维/二维局部极小值点；空心圆圈代表一维/二维局部极大值点。

（2）对f1和f2分别使用文献[11]中的方法建立多尺度极值点集S′和S″，设S′和S″的最高级数表示为n′和n″。

（3）将一维多尺度极值点集S′和S″中的各极值点子集按照各像素在原图像I中的位置生成对应的方向分离的2维极值点子集图，其中i=1,2,… ,n;j=1,2,… ,2i；n=min(n′,n″)为二维极值点最高级数。

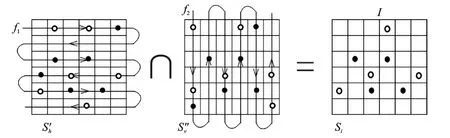
图2 由方向分离的极值点图合成的最终二维极值点图Fig.2 2-D MSE-scale extrema based on 1-D MSE-scale extrema

采用此方法生成的二维多尺度极值点在效果上相当于各级极值点在不同尺度的4邻域上查找获得。该方法生成二维多尺度极值点集的优点是速度快、可减弱大尺度级别上极值点稀疏的情况、自适应性强以及物理意义直观。

2 改进的快速自适应二维经验模式分解方法

2.1 快速自适应二维经验模式分解方法

文献[11]提出的快速自适应二维经验模式分解方法，即FABEMD方法在获得较好的分解效果的同时具有较快的分解速度，主要原因在于采用了一种新的求解局部均值的方法，基本思想是：用邻域窗口（通常是3×3邻域）比较方法找到图像I的局部极大值点集和极小值点集，由2个极值点间最小距离矩阵依据某种原则确定出滤波窗口尺寸wen作为图像I分解滤波的尺度。图像I上下包络的估计方法是FABEMD方法的核心：由极大值和极小值统计排序滤波器分别作用于I，生成图像I的上下2个包络曲面；但曲面并不光滑，因此再用算数平均滤波器对2个包络曲面进行平滑，得到最终的图像I的上下包络估计。

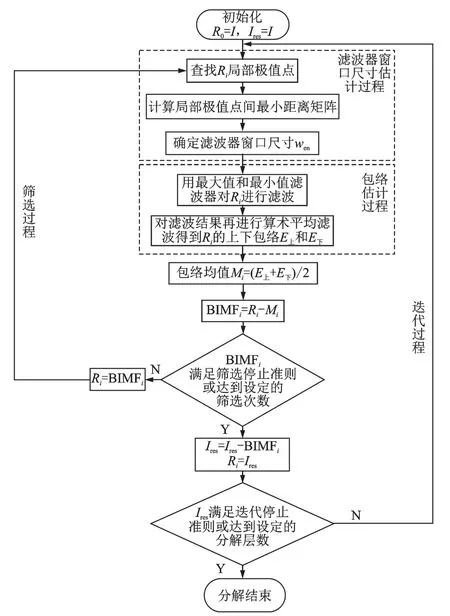
图3 FABEMD算法流程图Fig.3 Flow diagram of FABEMD

FABEMD方法的具体步骤如图3所示。其中BIMFi为第i级二维内蕴模式分量，Ires为余量，Ri为分解过程中间变量。wen的确定方法是：计算极值点最近距离矩阵dadj-max和dadj-min，两者都以降序排列，可以选用不同的准则从dadj-max和dadj-min中选择出滤波器窗口的尺寸wen。

然而，FABEMD方法中各级滤波窗口尺寸的计算效率不高，需要反复查找图像极值点、计算极值点间距离矩阵，不能自适应确定分解级数。文献[11]中提供的4种计算窗口尺寸的准则无法在得到分解结果前确定哪种是最佳的，即滤波窗口尺寸的确定具有很大的灵活性，也缺乏对信号的自适应性。

2.2 基于多尺度极值的改进FABEMD方法

针对FABEMD方法存在的不足，本文利用二维多尺度极值的各级极值点密度作为新的指标确定滤波窗口尺寸，提出一种改进的快速自适应BEMD算法，即IFABEMD方法，流程如图4所示，其具体步骤如下：

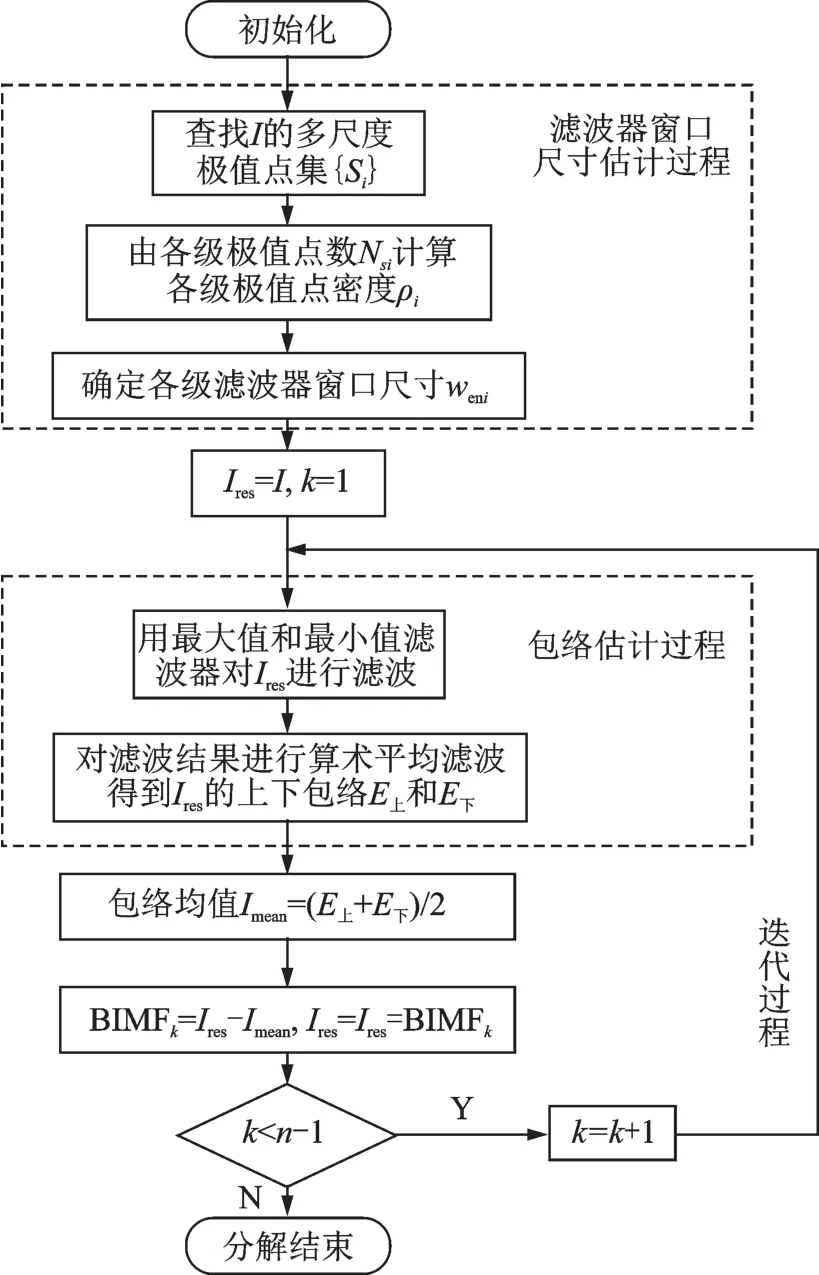
图4 改进的FABEMD算法流程图Fig.4 Flow diagram of IFABEMD

（1）由1.3节方法求出图像I的二叉树结构的多尺度极值点集S={Si}={S〈i,j〉},i=1,2,…,n;j=1,2,…,2i，其中n为多尺度极值点集最高级数。

（2）计算各极值点子集S〈i,j〉的极值点数目NSij，由此得到各级极值点的数目NSi为

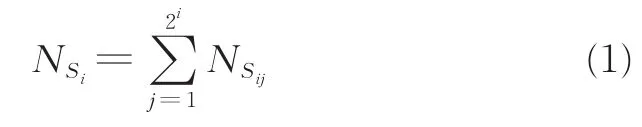
（3）计算各级极值点的平均密度为

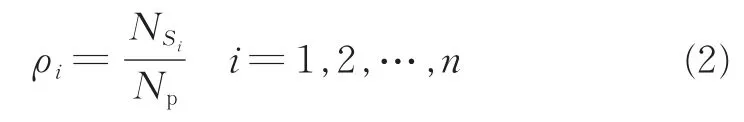
式中Np为图像I的像素总数。

（4）确定各级滤波窗口尺寸为

（5）设Ires=I，k=1。

（6）利用与FABEMD方法中相同的最大值/最小值统计排序滤波和平滑滤波方法，估计Ires的局部均值信号Imean。

（7）BIMFk=Ires-Imean，Ires=Ires-BIMFk。

（8）如果k＜n-1，则k=k+1，转到步骤（6），否则转到步骤（9）。

（9）分解结束。

由图3和图4的比较可以看出，IFABEMD算法的极值点查找和各级窗口尺寸计算不需要迭代，且各级滤波窗口尺寸随各级特征尺度的增加而自适应增大，与FABEMD分解结果相比减少了特征尺度不显著的多余分量，提高了分解的自适应性和效率。

3 仿真结果与性能分析

本文通过对典型的自然图像与合成纹理图像的实验仿真来验证上文介绍的二维多尺度极值查找方法和改进FABEMD方法的有效性。实验所用硬件配置为：Intel Core i5-7200U CPU，主频2.5 GHz和2.7 GHz，内存8 GB。所用代码均用Matlab语言实现。

3.1 3种二维多尺度极值点集建立方法的比较

不失一般性，以图5(a)Lena图像的多尺度极值点集为例，通过与基于p-邻域比较法和基于Voronoi多边形的邻域比较法进行对比，证明基于一维多尺度极值点集的二维多尺度点集生成方法的优点。3种方法所得Lena图像的1～4级极大值点集图如图5（b）―（d）所示，得到的各级极值点数及算法计算性能比较如表1，2所示。

图5 3种方法查找Lena图像的1～4级极大值点比较（白色点为极大值像素位置）Fig.5 Comparison of three methods for finding the maximum points of Lena image at levels 1―4(white points are the location of maximum pixels)

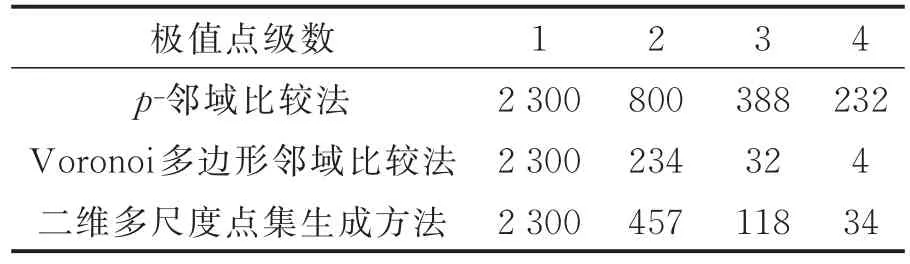
表1 3种多级极值点查找方法各级极值点数目比较Table 1 Comparison of the number of extrema at each level by three methods

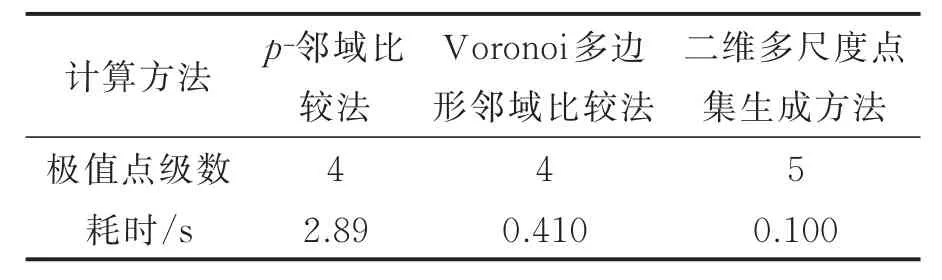
表2 3种多级极值点查找方法计算性能比较Table 2 Comparison of computational performance of three methods

由图5及表1，2可以直观看出，基于一维多尺度极值点集的二维多尺度点集生成方法既能自适应反映出信号的内蕴模式特征尺度，又能减弱极值点数目随极值点级数增加而过快稀疏，并且速度更快。

3.2 改进FABEMD方法分解实验结果

为了验证和分析改进FABEMD方法，即IFABEMD方法的有效性，下面分别给出原FABEMD方法和IFABEMD方法对典型的自然图像与合成纹理图像的分解对比结果。其中，FABEMD方法选用极值点最近距离矩阵dadj-max和dadj-min最小值中的最小值作为滤波窗口尺寸，并且筛选次数为1，迭代次数以分解效果与本文分解的最高级分量相当时为标准；IFABEMD方法不需要筛选过程，迭代次数为多尺度极值点集最高级数n-1（避免滤波窗口尺寸过大使分解速度快速下降）。实验图像如图6,7所示，图像参数如表3所示。FABEMD方法和IFABEMD方法的分解结果如图8—11所示。分解速度如表4所示。

由图8—11可以看出，不论对于自然图像还是合成纹理图像，FABEMD方法和IFABEMD方法分解结果均看不到伪像，并且各分量的物理意义更明显（FABEMD方法分解出的相互之间只有细微差别的多余分量在图中没有列出）。

图6 自然图像Fig.6 Natural images

图7 合成纹理图像及其组成分量Fig.7 Synthetic texture image and its components

表3 实验所用图像Table 3 Test images

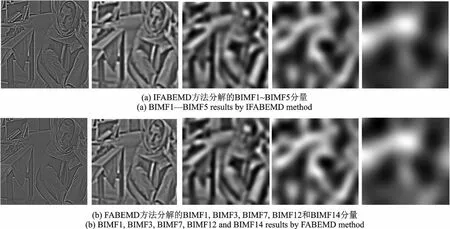
图8 Barbara图像分解结果比较Fig.8 Decomposition results by different methods for Barbara image

图9 Harbour图像分解结果比较Fig.9 Decomposition results by different methods for Harbour image

图10 D101纹理图像分解结果比较Fig.10 Decomposition results by different methods for D101 texture

图11 合成纹理图像分解结果比较Fig.11 Decomposition results by different methods for synthetic texture image

表4 不同方法分解速度比较Table 4 Comparison of decomposition speeds by different methods s

从图11与图7的对比可看出，FABEMD方法分解出的BIMF2是实际分量中不存在的一个频率分量，在IFABEMD方法中没有这个尺度的假分量。由表4可看出IFABEMD方法分解速度较FABEMD方法有明显提高，并且由表5可以看出IFABEMD方法分解出的内蕴模式分量数比FABEMD方法有明显减少。由表6可以看出当IFABEMD方法和FABEMD方法分解出的对应分量效果相同或相近时，有着相近的滤波窗口特征尺度，并且IFABEMD方法的滤波窗口特征尺度与分量效果的直观尺度更符合。

表5 不同图像中分解的最高层数Table 5 The highest levels of decomposition of different images

表6 滤波窗口特征尺度（像素宽度）Table 6 Feature sizes of filter windows（pixel width）

4 结束语

为了进一步提高现有FABEMD方法的信号自适应性与分解效率，本文提出了一种基于多尺度极值的改进FABEMD方法——IFABEMD方法。IFABEMD方法一方面提高了FABEMD方法在滤波窗口尺寸选择上的自适应性和该参数与分量特征尺度趋势的一致性，另一方面使分解速度更快、分解出的分量构成在视觉上更加合理。最后通过实验结果验证了本文方法的有效性和正确性。本文提出的基于尺度极值点集的IFABEMD方法为传统经验模式分解方法的研究提供了一个新的思路。该方法也为图像分析、图像融合和图像增强等应用提供了新的手段。然而对多尺度极值点集的构建方法和特性及其在BEMD方法中的应用还有待进一步深入研究。