基于正则化弱相关的分布式MWC重构算法

薛 欢，李 健，李 智

（四川大学电子信息学院，成都，610065）

引 言

随着通信技术的飞速发展，在诸多重要领域，宽带或者超宽带信号已成为主流，传统Nyquist采样方法所面临的高采样率是目前许多硬件设备无法完成的，而且采样后巨大的数据量给传输、存储和处理都造成极大的压力。压缩感知（Compressed sensing,CS）[1-2]的出现为信号的欠采样技术带来了契机，其中，调制宽带转换器（Modulated wideband converter,MWC）[3-5]从理论到实际硬件电路，实现了宽带稀疏信号的欠采样和盲重构。目前，MWC因其独特的优势被广泛应用于雷达[6]，信号参数估计[7]等领域。然而，当信号稀疏度变大时，MWC为保证重构性能需要成倍增加通道数为代价，过大的硬件开销显得不切实际。此外，在一些实际的分布式应用下，如认知无线电频谱感知[8-10]，单个MWC无法解决多径衰落、阴影等问题。

为了解决MWC面临的问题，分布式调制宽带转换器(Distributed modulated wideband converter,DMWC)[11]在MWC的基础上融入无线传感网络技术，该系统将每一个分布式感知节点看做MWC的一个通道，完成信号的采样，然后各节点将采样数据独立发送至融合中心，由融合中心作出统一判决。文献[12]引入马尔可夫随机场作为添加传感节点的选择方法，该方法提高了所选传感节点的质量，使DMWC即使在时变支撑集环境下，仍能完美重构信号支撑集。相继地，Eldar等提出了基于均匀线性阵列（Uniform linear array,ULA）的MWC系统[13],在完成信号欠采样的同时，通过阵列中各节点接收到的信号差异，得到信号的来波方向。同年，Wang等提出了基于互质阵列（Coprime array,CA）的MWC系统[14]，可进一步降低ULA-MWC系统的采样率。由此可见，基于多节点、分布式的频谱感知已经成为发展趋势，DMWC感知网络在实现分布式频谱感知领域中具有一定的研究价值。

在DMWC系统中，由于感知节点分布的位置不同，信号到达节点时存在一定的路径传输衰减。在信号传输衰减较小时，采用正交匹配追踪(Orthogonal matching pursuit,OMP)算法[15]即可实现信号的理想恢复，然而OMP算法迭代过程需要依赖信号稀疏度作为收敛条件。为了使DMWC更贴合实际的应用，本文提出基于正则化弱相关的DMWC重构算法（RwcOMP），与OMP不同的是，RwcOMP结合了“弱相关性”原则和正则化标准来筛选索引集，可提高原子的准确性和效率，最后再由支撑集越界条件，删除索引集中无效的原子，得到最终的支撑集。仿真结果表明，在信号稀疏度未知时，DMWC采用RwcOMP算法，能大大提高自身对信号传输衰减的容忍度；此外，与原来的OMP算法相比，RwcOMP算法重构效果更佳。

1 DMWC系统模型

DMWC是压缩感知和多节点协作频谱感知的相互结合。如图1所示，整个系统模型包括一个信号源、m个分布式感知节点以及一个融合中心。每一个分布式节点可看作MWC的一个通道，节点中包含随机混频、低通滤波、低速采样模块，各节点独立地执行信号的欠采样任务，然后再将压缩采样数据发送到数据处理中心，由融合中心对欠采样数据做出统一的判决。

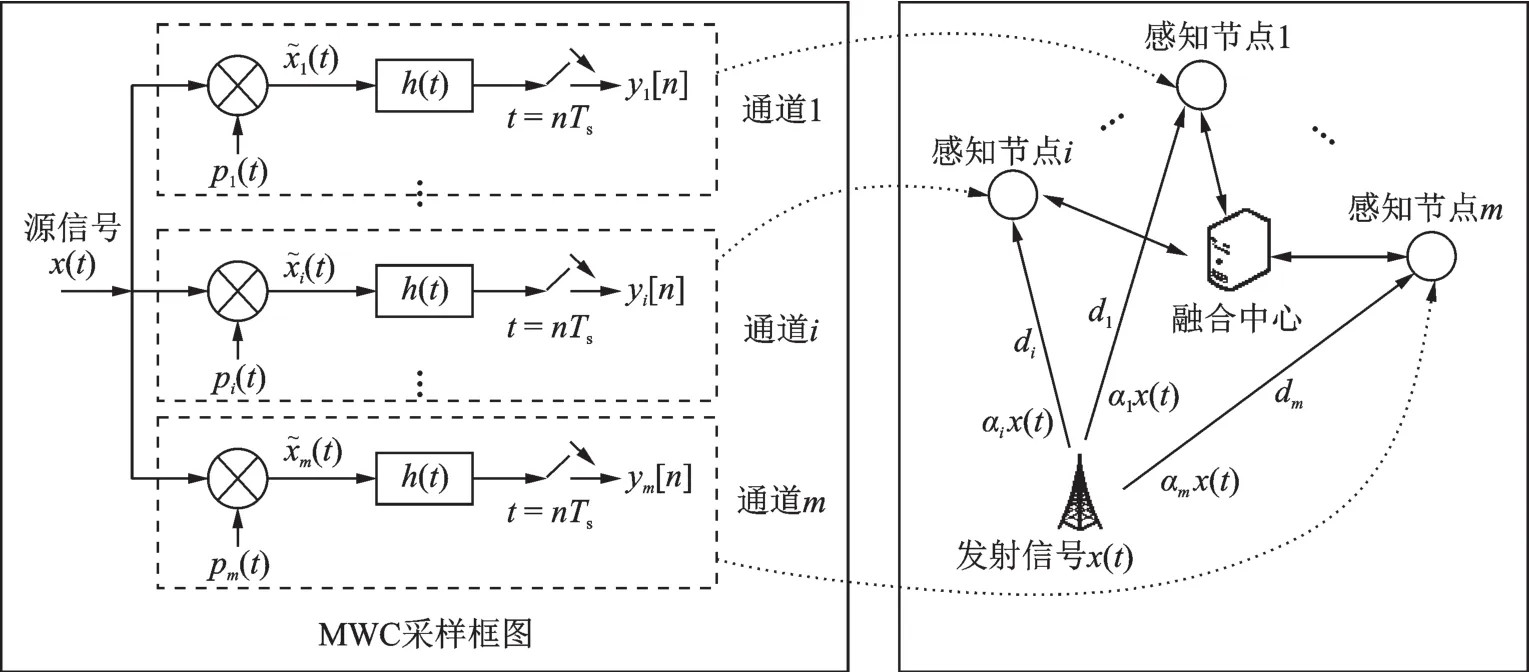
图1 DMWC协作频谱感知网络Fig.1 DMWC collaborative spectrum sensing network

由于源信号在实际传输过程中存在一定的路径损耗，各分布式感知节点的接收信号必然存在差异。如图1所示，设基站发射的源信号为x(t)，每一个感知节点与源信号的距离为di(i=1,2,3,…,m)。对于融合中心而言，节点与基站的距离是已知的，即di是先验知识。设αi是第i个节点接收信号xi(t)相对于x(t)的路径传输衰减系数，可定义为节点接收信号功率与源信号功率的比值，根据电磁波在室外的传输模型，αi可表示为

式中：Pa表示接收功率，Pt表示发射功率，G表示系统增益，λ表示信号波长，F表示表示系统损耗因子。如图1所示，第i个感知节点的接收信号xi(t)可表示为

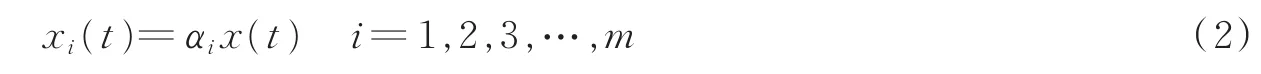
式中αi∈(0,1]。DMWC感知节点分布的位置不同，信号到达节点时存在不同的路径传输损耗，因此，可结合先验知识，根据式（1）估计αi的值。此外，文献[11]指出，当αi≥0.8，DMWC频谱重构性能不受传输衰减的影响。

如图2（a）所示，在第i个通道中，节点接收信号αix(t)与混频序列pi(t)相乘后，输出信号的傅里叶变换如下

混频函数的参数如图2(b)所示，从式（3）可以看出，混频的过程实质是将信号频谱以fp为步长搬移到基带。再经低通滤波后，以1/Ts的速率采样，第i个通道的输出采样序列yi(n)的离散时间傅里叶变换表示为

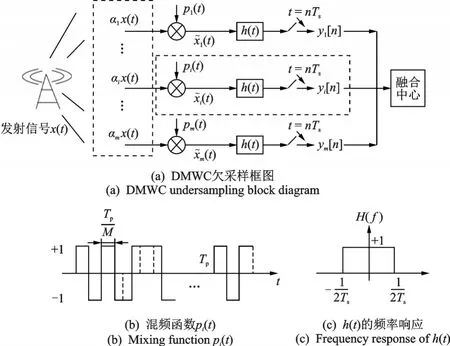
图2 DMWC系统及其参数示意图Fig.2 Schematic diagram of DMWC system and its parameters

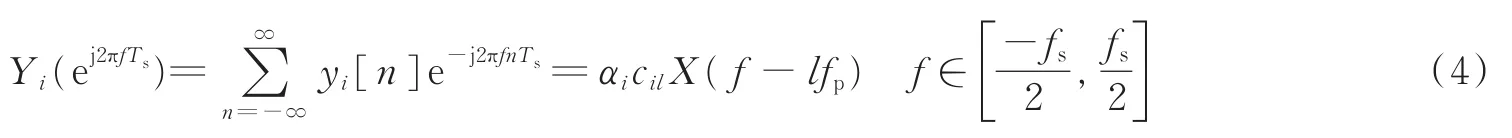
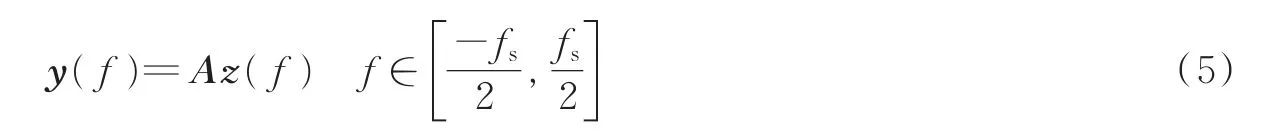
式中：y(f)为长度为m的向量。未知向量z(f)=[z1(f),…,zL(f)]T的长度为zi(f)=X(f+(i-L0-1)fp),1≤i≤L,f∈FS，测量矩阵A的元素取值为由于cil的伪随机特性，A依然是一个随机测量矩阵，满足RIP性[16]。

在融合中心从样本序列yi[n]恢复原信号x(t)可归结为求式（5）的最稀疏解z(f)，其融合规则主要是通过图3所示的从连续到有限（Continuous to finite,CTF）模块重构信号支撑集S。

图3 CTF模块Fig.3 CTF module

图中，构造低维矩阵V的方式为

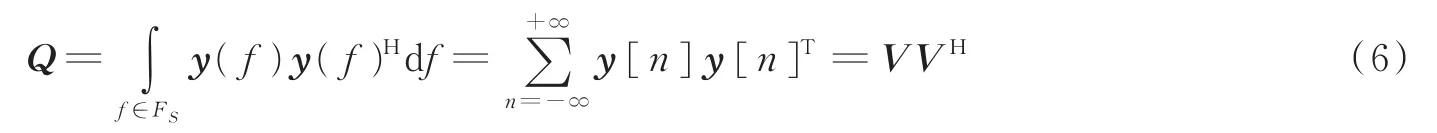
式中：y[n]=[y1[n],…,ym[n]]T是在nTS时刻的采样矢量，对Q特征值分解后即可得到降维后的矩阵V，进而构造出图3所示的新多测量向量模型V=Az(f)，采用OMP算法求出最稀疏解z(f)，即可得到原信号的支撑集S，一旦求得信号的支撑集，则可根据式（7）求得原信号。

式中：z[n]=[z1[n],…,zL[n]]T,zi[n]是zi(f)的反离散时间傅里叶变换，支撑集是频谱切片Zi(f)非零子带的所在位置。

2 基于正则化弱相关的DMWC重构算法

由于OMP算法需要已知稀疏信号的频带数作为停止迭代的条件之一，而实际的电磁频谱环境下，信号的稀疏度是难以获得的。为了使DMWC更加贴合实际应用，本文提出了一种基于正则化弱相关的DMWC重构算法，该算法不依赖信号稀疏度作为收敛条件，通过给定一个固定的迭代次数Iter，即可高概率重构信号支撑集。在具体介绍RwcOMP算法流程时，首先引入原子“弱相关性”的概念，它表示每次迭代是按门限值th来选取一定数量的弱相关原子，而不是仅选取一个相关性最大的值，门限值计算为

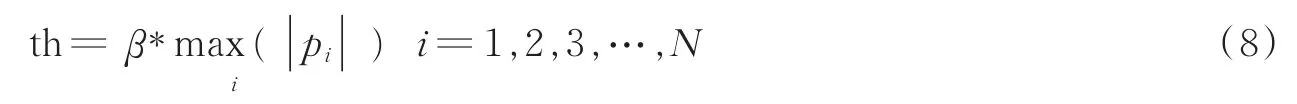
式中：门限参数的取值β∈(0,1]；pi是测量矩阵各列向量与残差矩阵的内积值，可用于表示向量之间的相关性。当pi大于该门限时，就可通过初选加入索引集J。然后将索引集正则化，符合条件的原子才能加入支撑集候选集Λt。接着更新残差，直到残差的能量达到设定的阈值，则停止迭代；最后判断支撑集是否越界，删除其中相关性较小的无效原子。其中，正则化可表示为

图4给出了RwcOMP算法的具体流程。

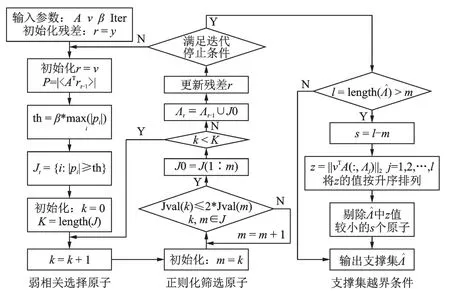
图4 RwcOMP算法流程图Fig.4 RwcOMP algorithm flow chart

3 仿真实验

仿真实验的原始信号是宽带稀疏多子带调制信号x(t)，设置信号频带数N=4，其信号时域模型为

式中：能量系数Ei={1,2}，带宽B={50,50,50}MHz，时间时延τi={0.7,0.4}，fnyquist=10 GHz，fi∈[0,fnyquist/2]，fs=fp=fnyquist/195≈51.3 MHz。为了体现抗噪性能，在原始调制信号中加入高斯白噪声w(t)，即仿真的信号是x(t)+w(t)，信噪比SNR=10log(‖x‖2/‖w‖2)。所有实验都进行500次蒙特卡洛循环。

为了找到RwcOMP算法的最佳门限参数，实验设置通道数m={15,20,25,30}，迭代次数S=10，传输衰减系数αi=0.8，对比不同信噪比下，门限参数β从0.4增大到1.0时，支撑集恢复成功率pr的情况，如图5所示。其中，pr的计算参照文献[3]。在一定通道数和信噪比的条件下，pr随着门限参数的变大而逐渐提高，当β增大到一定限度时，若再继续增大反而会使恢复率降低。从图5（a）—（d）的全局对比来看，在本文设置的参数条件下，β的最优值取0.9。

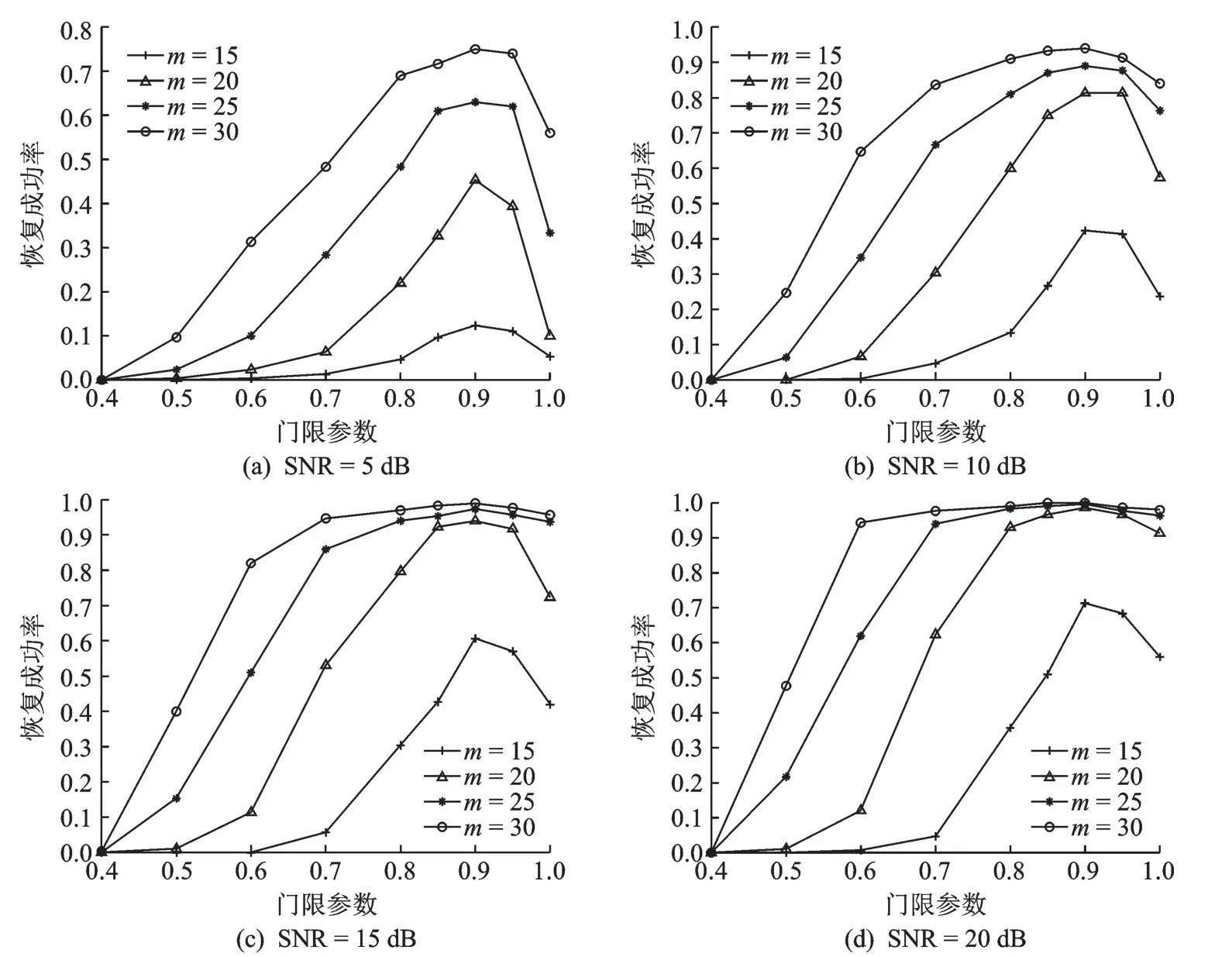
图5 门限参数和支撑集恢复成功率的关系Fig.5 Relationship between threshold parameters and the support set recovery

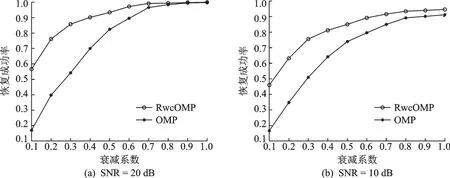
图6 衰减系数和支撑集恢复成功率的关系Fig.6 Relationship between attenuation coefficient and the support set recovery

由于DMWC感知节点分布位置不同，节点接受信号存在不同程度的传输衰减，为了验证在不同的传输衰减下，RwcOMP算法的恢复效果，设置衰减系数αi在区间[0.1,1]以1为步进时，对比RwcOMP算法和OMP算法下DMWC支撑集恢复成功率。如图6所示，在一定信噪比下，αi增大，表明信号的路径损耗越小，支撑集恢复成功率也增大，当衰减系数等于1时，此时信号不存在路径传输损耗，支撑集恢复率受SNR的影响，而与αi无关。在SNR较高时（SNR=20 dB），衰减系数αi≥0.4，RwcOMP算法的恢复率就能达到90%以上，对比OMP算法，则需要αi＞0.6时，支撑集恢复率才能达到90%以上。当信号存在严重的传输衰减时，如αi=0.3，在SNR为10和20 dB时，OMP算法的支撑集恢复率都非常低，但是RwcOMP恢复成功率比OMP分别提高了24.6%，31.6%。由此可见，RwcOMP算法大大提高了DMWC对传输衰减的容忍度。

在DMWC重构过程中，支撑集恢复率除了受传输衰减的影响，感知节点数目也是影响恢复率的因素之一。图7给出了在一定信噪比下，通道数在区间[15,35]内以1为步长变化时，RwcOMP算法和OMP算法的支撑集恢复情况，其中衰减系数取0.8是为了减少信号传输衰减对实验结果的影响。从图可以看出，随着通道数的增加，两种算法的支撑集恢复率都在提高，在信噪比分别为5和15 dB的情况下，RwcOMP算法的恢复成功率在m的整个区间范围内均优于OMP算法。由此可见，RwcOMP具有一定的抗噪性能。

图7 通道数与支撑集恢复成功率的关系Fig.7 Relationship between the number of channels and the support set recovery

图8给出了在一定信噪比下，两种算法频带数与支撑集恢复率的关系，其中，衰减系数为0.8，频带数N∈[2,14]。在N≤6时，RwcOMP算法具有更好的恢复性能，如SNR=20 dB时，RwcOMP恢复率为98.4%，而OMP仅92.2%；当N＞6时，由于通道数目的限制，两种算法的恢复性能都急剧下降。当N＞12时，两种算法几乎都无法恢复支撑集，因为此时的信号不再视为稀疏信号。

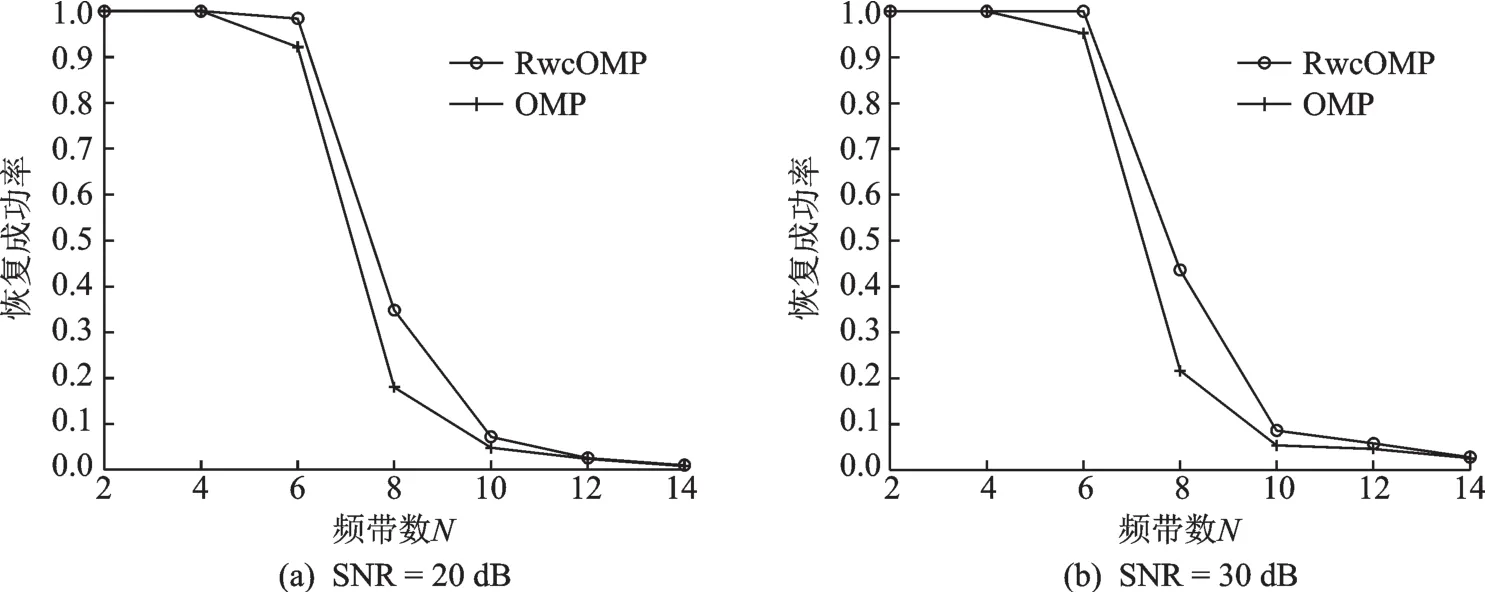
图8 频带数与支撑集恢复成功率的关系Fig.8 Relationship between the number of signal bands and the support set recovery

4 结束语

新近提出的DMWC系统具有灵活的分布式感知节点，能应对时变信号时系统节点数目的弹性变化，提高感知准确率。由于在实际电磁频谱感知场景下，宽带稀疏信号的频带数难以预知。因此，本文提出了基于弱相关性正则化的DMWC重构算法，该算法不依赖信号稀疏度作为迭代收敛条件。仿真结果表明，信噪比足够时，RwcOMP算法在保证重构精度高于90%的前提下，对传输衰减的容忍度提升至0.4。此外，在同等条件下，RwcOMP算法的恢复性能优于OMP算法。综上所述，本文所提算法从理论上进一步提高了DMWC的实际应用前景及价值。