稻谷堆修正剑桥模型参数的测定及含水率对其影响
陈 雪 程绪铎 龙 桃 成嘉慧 胡丹丹 王江粉
(南京财经大学食品科学与工程学院;江苏省现代粮食流通与安全协同创新中心, 南京 210046)
稻谷储藏在粮仓中,稻谷堆在自重与仓壁反力的作用下,将产生应力。由于稻谷籽粒松软,稻谷堆在应力的作用下,产生弹性和塑性形变[1],稻谷堆的密度增大,孔隙率减小。同一粮层的应力、应变、密度、孔隙率是不均匀的。随着粮层深度的增加,粮层的应力、密度增大,孔隙率减小。为了探究粮仓中稻谷堆的应力,密度及空隙率的分布情况,就要选择合适的稻谷堆的应力-应变本构方程。Roscoe等[2]研究者建立了最初的剑桥模型,随后,Burland[3]通过研究认为剑桥模型屈服面轨迹应为椭圆,并根据新的塑性功方程重新推导了屈服方程。1968年,Roscoe等[4]又对自己的观点做出修正,提出了修正剑桥模型(Modified Cam Clay)。修正剑桥模型以体积应变与剪切应变作为应变量,且屈服面为平均主应力屈服面,适合稻谷堆大体积变形的特征。修正剑桥模型的参数少,易于测定,所以修正剑桥模型非常适合于研究稻谷堆的应力应变分布问题。若要使用修正剑桥模型,必须要先确定该模型参数,目前鲜见对稻谷堆修正剑桥模型参数测定的研究的报道。
本文采用TSZ-6A应变控制式三轴仪测定稻谷堆的修正剑桥模型参数M、κ、λ、E、υ,由弹性理论与实验数据推导出弹性模量E与围压σ3的关系式,由粮食孔隙测定仪测定出稻谷堆修正剑桥模型参数初始孔隙比e0。
1 修正剑桥模型
修正剑桥模型是一个用弹塑性增量理论描述应力-应变关系的弹塑性本构模型[4]。在外力作用下,物体产生的应变增量包括体积应变增量dεv和剪切应变增量dεs,分别由弹性应变增量和塑性应变增量两部分组成:
(1)
(2)
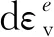
修正剑桥模型本构关系就是弹性应力应变关系与塑性应力应变关系。在修正剑桥模型中,广义剪切力q=σ1-σ3,平均主应力p=(σ1+2σ3)/3;破坏点时,q=(σ1-σ3)max。
修正剑桥模型中弹性应力应变关系[6]为
(3)
(4)
(5)
式中:κ为等向膨胀指数;e0为初始孔隙比;ν为泊松比;E为弹性模量/kPa。
修正剑桥模型中塑性应力应变关系为[7,8]
(6)
(7)
式中:η=q/p,M为临界状态应力比,λ为对数硬化模量。
总体积应变增量等于弹性体积应变增量与塑性体积应变增量的和[9],根据经典弹塑性理论,我们可以得到修正剑桥模型的显性表达式,本构等式可以写成以下形式:
(8)
(9)
(10)
(11)
(12)

因此,修正剑桥模型需要确定的参数包括临界状态应力比M、等向膨胀指数κ、对数硬化模量λ、弹性模量E、泊松比υ、初始孔隙比e0。
2 稻谷堆修正剑桥模型参数测定方法
2.1 试验材料
镇稻18号稻谷,产地江苏镇江,原始含水率为12.93%w.b.,将稻谷含水率调节为: 9.21%、11.30%、12.93%、15.16%、16.96% w. b.。
2.2 试验仪器
TSZ-6A应变控制式三轴仪,AL204 型分析天平,JSFD - 粉碎机,LKY-1型粮食孔隙率测定仪。
2.3 试验方法
2.3.1 初始孔隙比e0的测定
粮食孔隙率ε为粮食中孔隙与整个粮食容积之比[10]。孔隙比e指粮食中孔隙体积与粮食籽粒体积之比,孔隙比可由孔隙率推导计算得到。本试验通过LKY-1型粮食孔隙率测定仪(见图1)测定粮食的孔隙率。
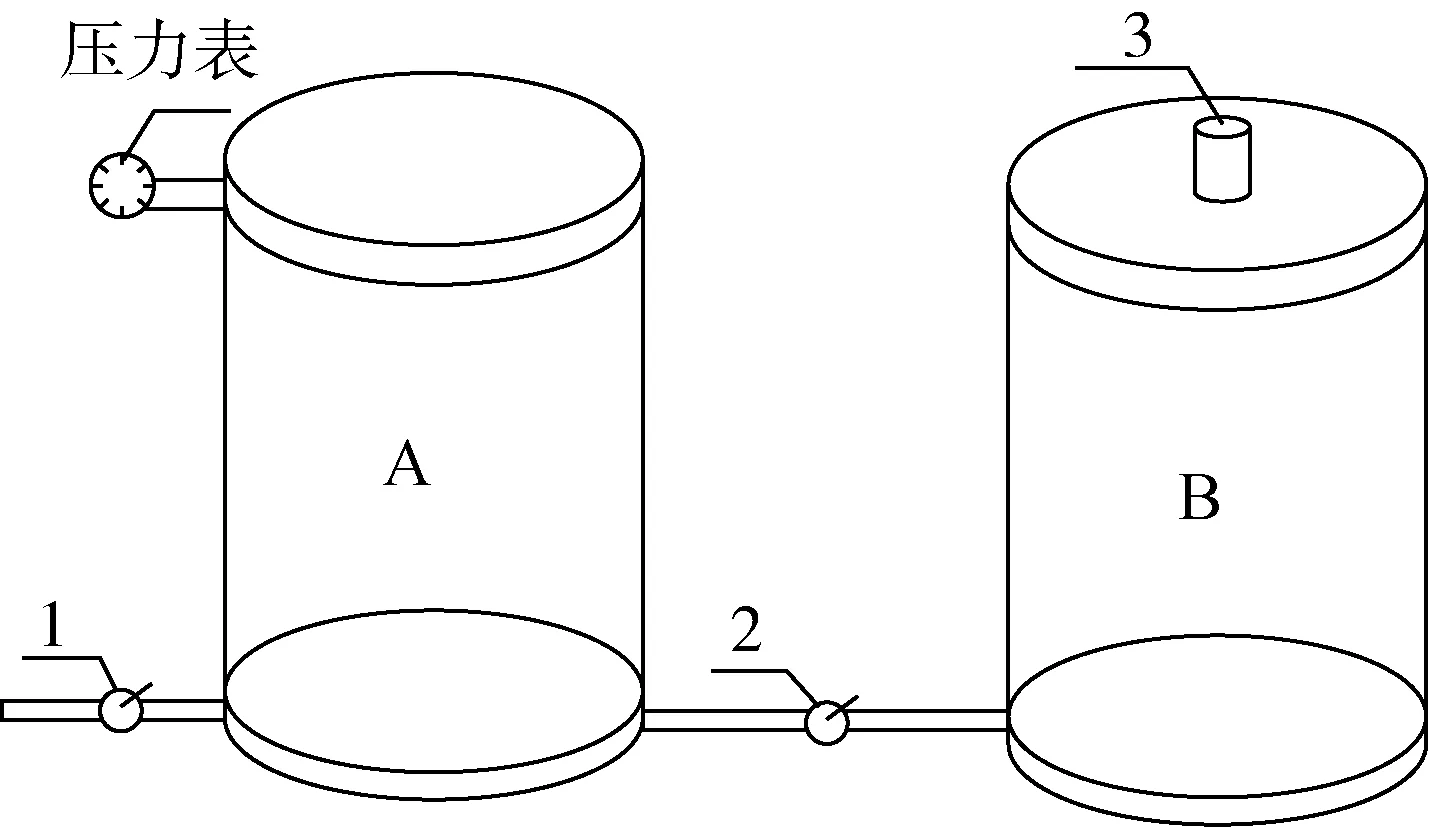
图1 孔隙率测定仪示意图
如图1所示,两个容积相等的压力容器A和B,在容器B中装满样品并将其密封。关闭阀门2,打开阀门1、3,用空气压缩机向容器A中鼓进一定压力的气体。当压力表指针达到一定数值时,关闭阀门1,当压力值稳定后,记下压力表读数P1;关闭阀门3,然后打开阀门2,当容器A和B中压力平衡时,记下此时压力表读数P2。视空气为理想气体,由理想气体等温过程的特性推出孔隙率如下:
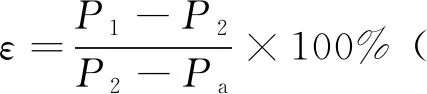
一个大气压下的样品初始孔隙率为:
ε=(V0-V固)/V0
(13)
V固=V0(1-ε)
(14)
则初始孔隙比为
e0=V孔/V固=(V0-V固)/V固
(15)
故e0=ε0/(1-ε0)
(16)
式中:V为样品体积/m3;V固为样品籽粒的体积/m3;V孔为样品中孔隙的体积/m3;V0为样品初始体积/m3。
2.3.2 临界状态应力比M的测定
对样品进行轴向压缩试验测定临界状态应力比M。在轴向压缩试验中,选定五个围压σ3:30、50、70、90、110 kPa。装好样品后,启动仪器对样品进行剪切(剪切应变速率为1.000 mm/min),位移每增加0.4 mm,记录一次测力计读数和样品体积减少量,直至测力计读数出现峰值时,记下峰值时p和q值。对每一个围压,试验重复三次。将这5组试验的破坏点(即最大主应力差)所对应p和q绘制在p-q平面中,经一元线性回归得直线的斜率M值。
2.3.3 对数硬化模量λ和等向膨胀指数κ的测定
通过各向等压试验测定对数硬化模量λ和等向膨胀指数κ,使围压σ3从0 kPa增加至200 kPa,围压每增加5 kPa,记录一次样品体积减少量,待围压增至200 kPa,再依次卸载至0 kPa,同样每减小5 kPa,记录一次样品体积增加量。将加载曲线和卸载曲线上的p和所对应的孔隙比e绘制在e-lnp平面中,经一元线性回归得直线的斜率λ和κ值。
2.3.4 弹性模量E和泊松比υ的测定
2.3.4.1 加卸载弹性模量E
进行轴向加卸载循环的常规三轴压缩试验,设定围压σ3分别为30、50、70 、90 、110 kPa,测定稻谷堆的弹性模量E和体变模量B。在三轴压缩试验中,稻谷堆样品呈圆柱形,轴向压力为σ1,围压为σ3,主应力差为Δσ=σ1-σ3,当主应力差达到最大值时稻谷堆破坏。对于每一个围压σ3,可测定一个最大主应力差。
本试验主要参照土的试验规程中的测定弹性模量试验SL237-029—1999[11]。在轴向压缩试验确定了最大主压力差后,选取最大主应力差的1/10,逐级加压和卸压,施加第1级压力,并开动秒表,记录加压后1 min时位移计的读数,每隔1 min施加一级压力,测记位移计读数,施加到第4级压力为止;随后逐级卸压,每隔1 min卸去一级压力,并测记卸压后1 min时位移计的读数,直至施加的轴向压力全部卸去;重复加卸载4次后,持续加压直至破坏。
弹性模量按最后一次加卸载中测定的数据计算:
(17)
式中:E为粮堆的弹性模量/kPa;ΔP为轴向荷载/kPa;Δhe为粮堆的弹性变形量/mm;hc为试样固结后的高度/mm。
2.3.4.2 泊松比υ
由等向压缩试验的卸载曲线可得到体变弹性模量, 体变弹性模量按式(18)计算:
(18)
式中:B为粮堆的体变弹性模量/kPa,Δv为粮食的弹性体积增量,m3;V为试样固结后的体积/m3。
泊松比υ按式(19)计算:
ν=(3B-E)/6B
(19)
2.4 试验结果与分析
2.4.1 初始孔隙比e0
通过LKY-1型粮食孔隙率测定仪测定不同含水率稻谷堆的初始孔隙率。孔隙比可由孔隙率计算得到。稻谷品种为镇稻18号,含水率分别为9.21%、11.30%、12.93%、15.16%、16.96% w.b. 的稻谷堆的初始孔隙比e0为1.144 1、1.173 0、1.187 2、1.238 1、1.296 2。初始孔隙比随着含水率的增加而增加。
2.4.2 临界状态应力比M
通过TSZ-6A 应变控制式三轴仪在围压为30、50、70、90、110 kPa条件下,对稻谷堆(镇稻18号,9.21%,11.30%,12.93%,15.16%、16.96% w.b.)进行轴向压缩试验,将每个样品所得到的5组不同围压所对应的p和q绘制在p-q平面中,经一元线性回归方程得到直线的斜率M值,即为临界状态应力比M。由计算可知,稻谷堆含水率为9.21%、11.30%、12.93%、15.16%、16.96% w.b.的临界状态应力比M分别为2.027 3、1.807 9、1.949 7、2.027 3、1.761 9,临界状态应力比与含水率之间无显著性关系。
2.4.3 对数硬化模量λ和等向膨胀指数κ
根据确定的实验条件,先进行试验测得稻谷在各个含水率下的孔隙率,计算得到相应的孔隙比,然后在围压为30、50、70、90、110 kPa条件下,对稻谷堆(镇稻18号,9.21%、11.30%、12.93%、15.16%、16.96%w.b.)进行各向等压压缩试验,将加载曲线上lnp(p=σ3,p分别为30、50、70、90、110 kPa)与相应e对应绘制在平面中,经一元线性回归得到斜率λ;同样地,将回弹曲线上lnp(p分别为30、50、70、90、110 kPa)与相应e对应绘制在平面中,经一元线性回归得到直线的斜率κ。不同水分稻谷堆的e-lnp曲线见图2。
由图2可知,含水率分别为9.21%、11.30%、12.93%、15.16%、16.96% w.b.的稻谷堆对数硬化模量λ分别为0.165 8、0.168 5,0.168 8、0.170 5、0.174 7;等向膨胀指数κ分别为0.130 6、0.133 8、0.134 5、0.136 6、0.138 5。对数硬化模量λ和等向膨胀指数κ随着含水率的增大而增大。
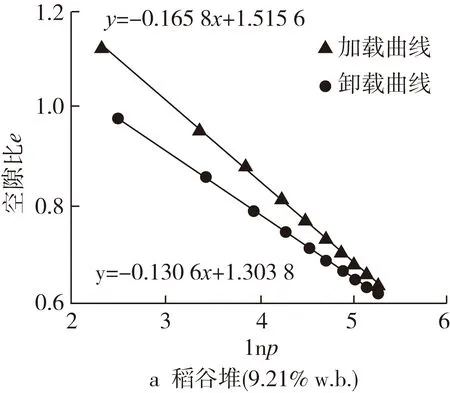
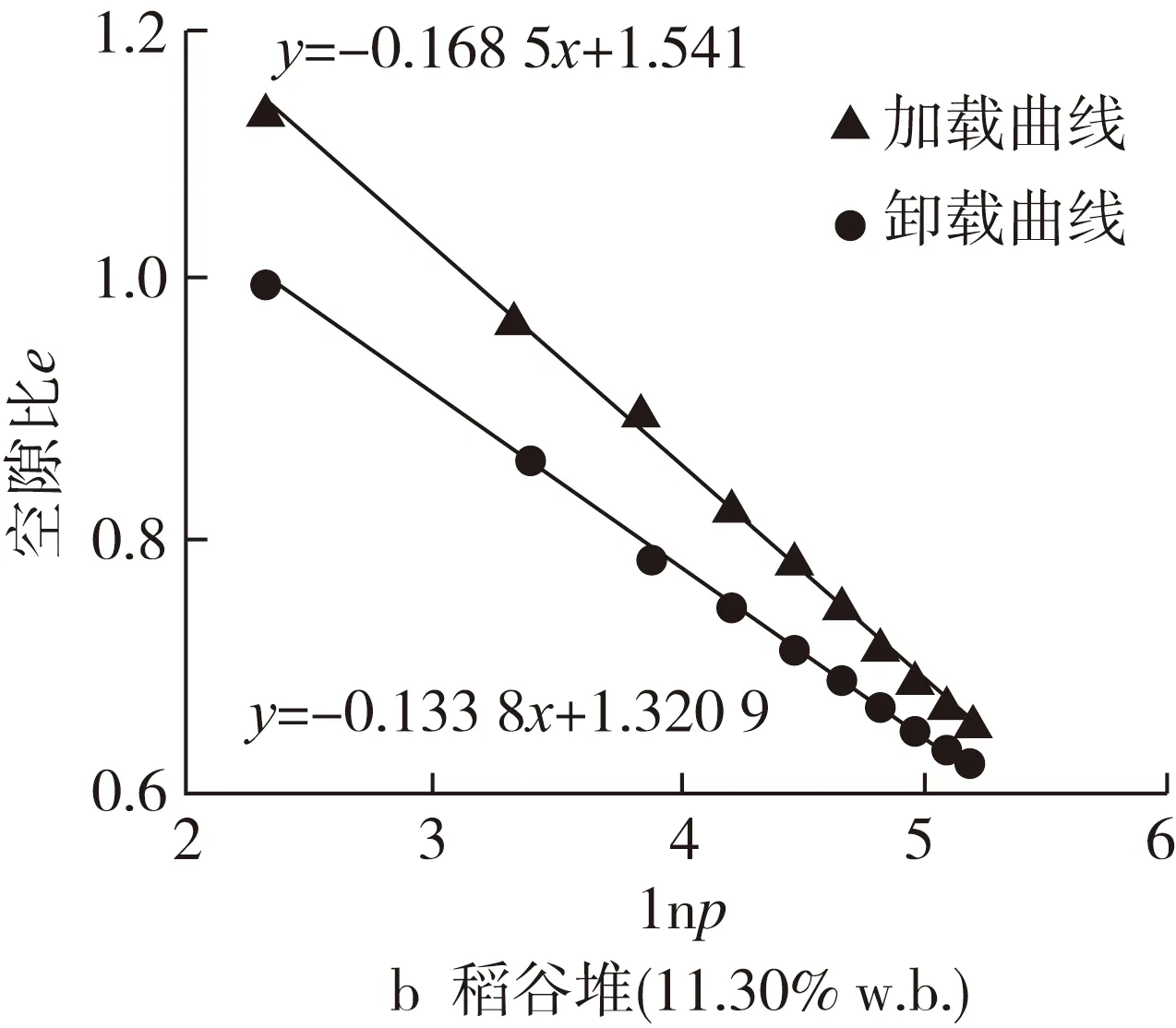

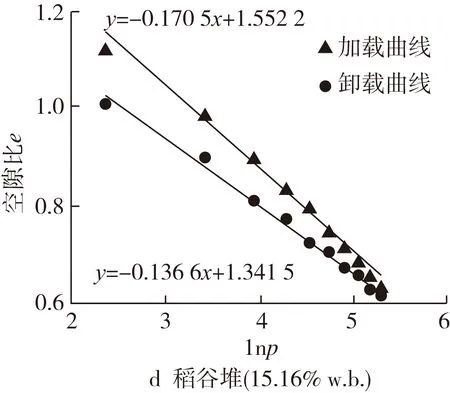
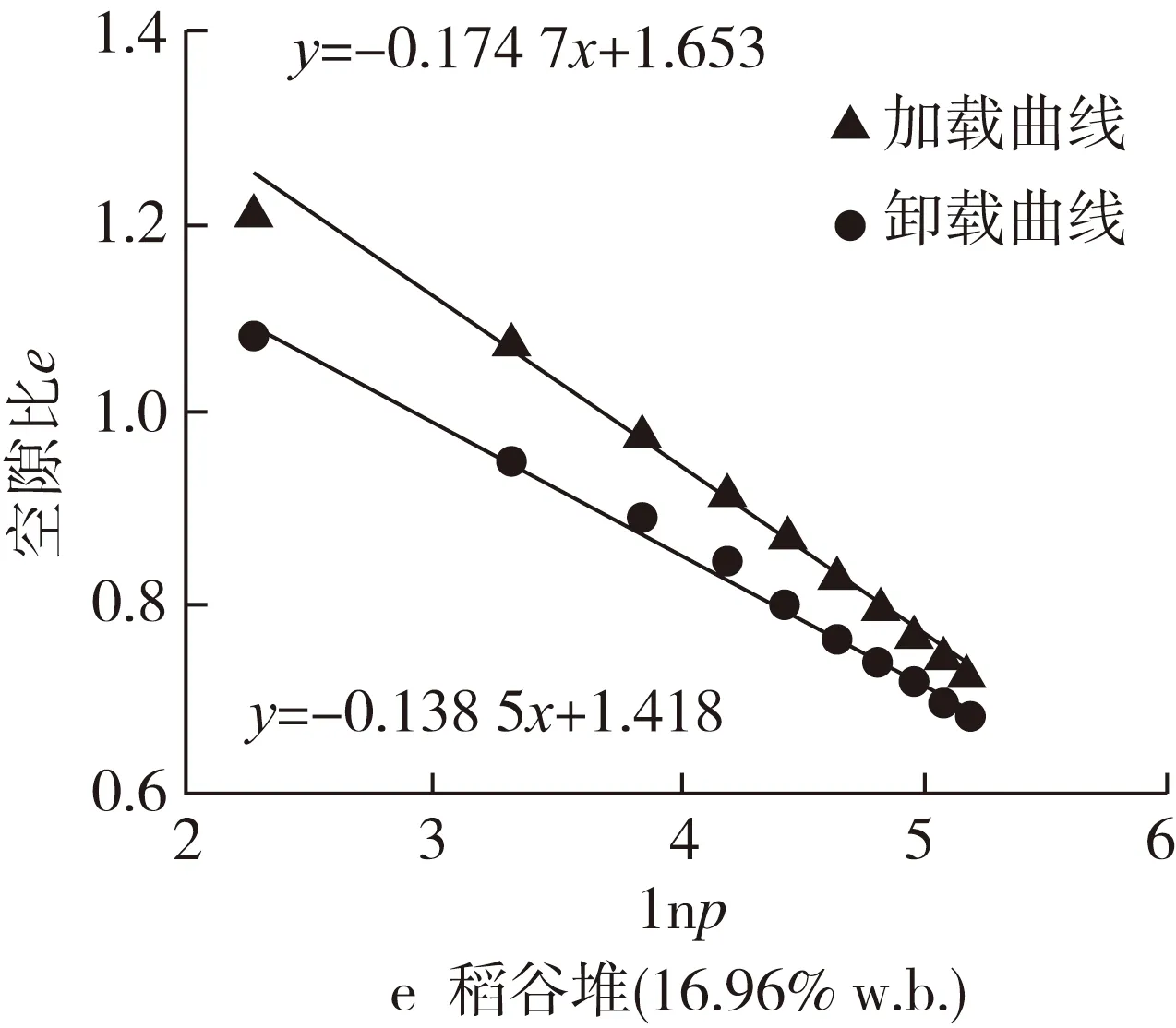
图2 不同含水率稻谷堆的e-lnp曲线
2.4.4 弹性模量E和泊松比υ
通过加卸载循环的三轴压缩试验,在不同含水率、不同围压下的稻谷堆的弹性模量E、体变模量B和泊松比υ可由式(17)、式(18)、式(19)计算得到,如表1所示。

表1 不同含水率、不同围压下稻谷堆的弹性模量、体变模量和泊松比
由表1结果可知,泊松比υ与含水率无显著关系。
由三维胡克定律[12]设定弹性模量E与围压σ3的关系式为:
E=KPa(σ3/Pa)n
(20)
K为弹性模量数, 无量纲;n为弹性模量指数, 无量纲;Pa: 大气压力,(F/L2);σ3: 围压, (F / L2)
由式(20)可得
log(E)=log(KPa)+nlog(σ3/Pa)
(21)
根据式(21),由表1中的弹性模量E与围压σ3在logE- log(σ3/Pa)平面上绘制一元线性回归直线见图3。
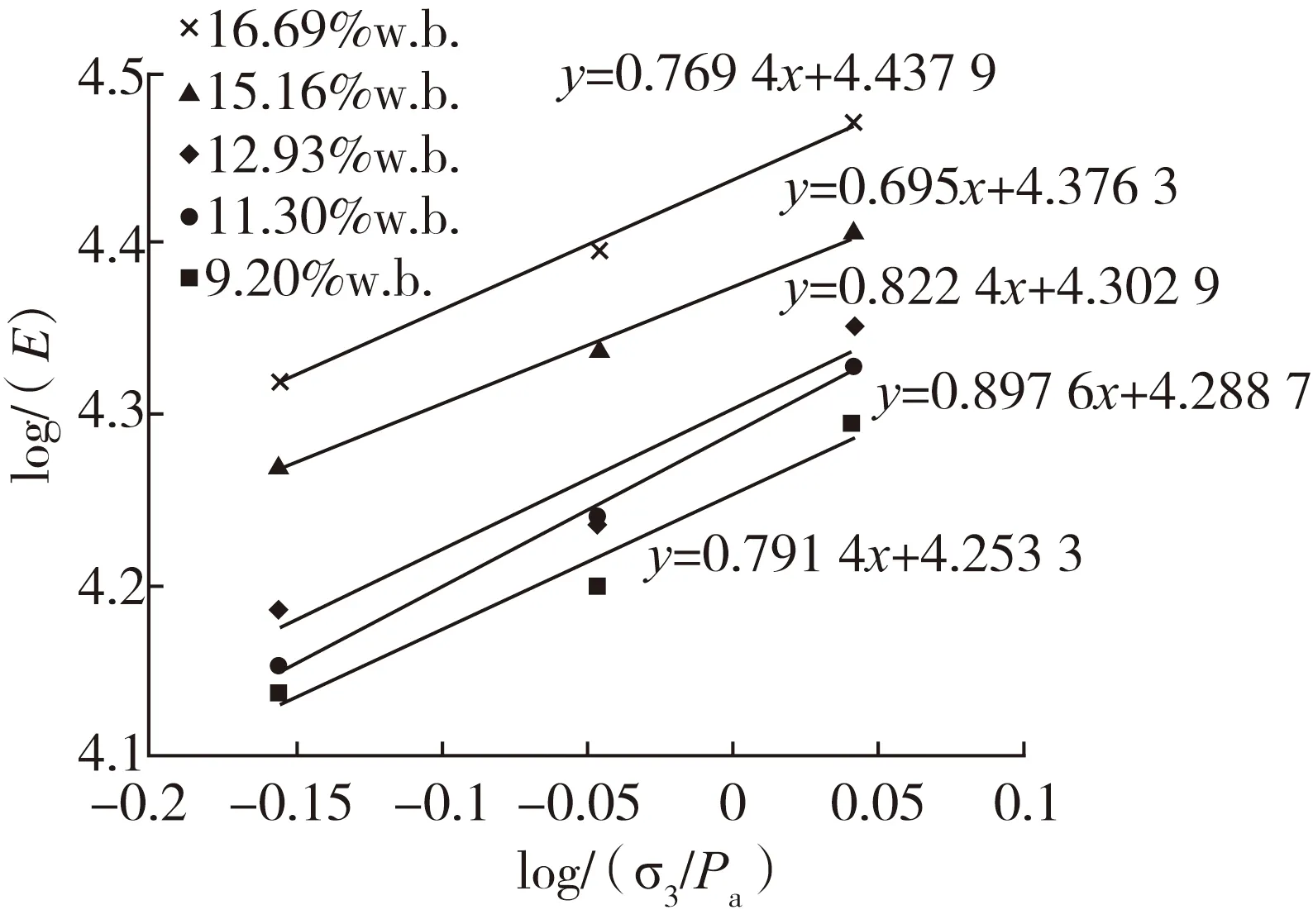
图3 不同含水率的稻谷堆的log E - log( σ3 /Pa) 曲线
通过图3中5条直线的斜率和截距计算可得,稻谷含水率为16.96%、15.16%、12.93%、11.30%、9.20% w.b. 的K分别为274.09、237.85、200.86、194.4、179.18;n分别为0.769 4、0.699 5、0.822 4、0.897 6、0.791 4。其中含水率越高,K的值越高。
2.4.5 测量结果
经计算后,不同含水率稻谷堆的修正剑桥模型参数见表2。
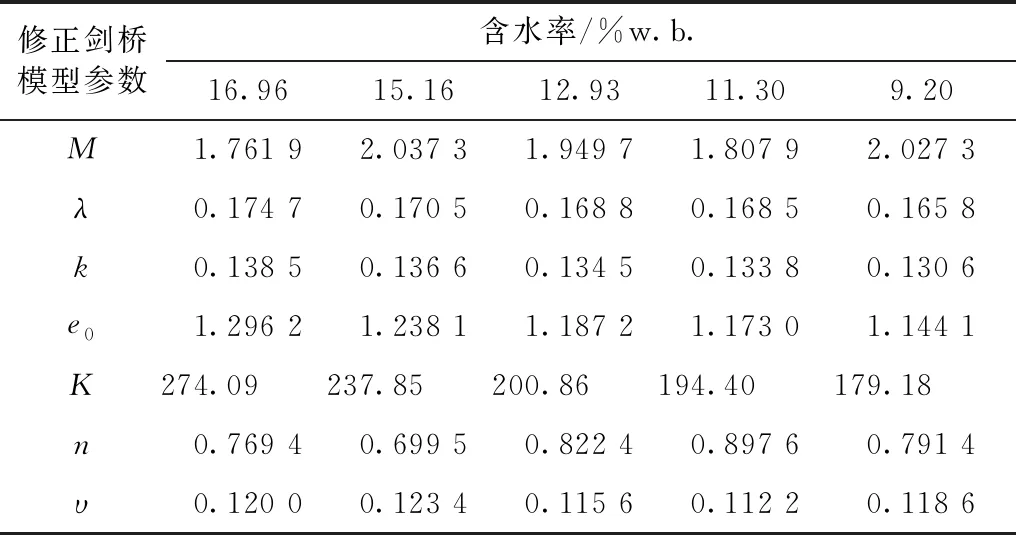
表2 不同含水率镇稻18号的修正剑桥模型参数
3 结论
稻谷堆(镇稻18号)修正剑桥模型参数中的对数硬化模量λ、等向膨胀指数k、初始孔隙比e0均随着含水率的增大而增大,临界状态应力比M与含水率无显著性关系。
稻谷堆(镇稻18号)在含水率范围为9.21%~16.96% w.b.时,围压为30~100kPa时,弹性模量E的范围为9.91~25.67 MPa,泊松比υ的范围为0.10~0.15。弹性模量E与围压σ3的关系式为E=KPa(σ3/Pa)n,其中弹性参数K随含水率的增大而增大,参数n与含水率无显著相关性。

