浅析初中数学证明题的解题策略

王喜明

摘 要：证明题是初中阶段数学教学重点与难点，极受广大师生重视，其解答具有一定解题策略与技巧，解题策略可帮助学生在短时间内快速掌握该类习题解题方式与思路，对学生学习效率提升有极为积极的影响。本文将以人教版初中数学教材为例，对初中数学证明题解题策略展开深层次分析，期望能够为学生证明题的解题能力提高提供一定帮助。

关键词：审题;解题策略;人教版;数学证明题;联想法

【中图分类号】G633.6 【文献标识码】A 【文章编号】1005-8877（2020）09-0096-01

1.证明题解题基本步骤

具体解题步骤如下：

（1）审题

审题是数学题解题关键，在具体进行证明题解题之前，学生需要通过仔细审题，明确题目中给出的已知条件与题意，对其展开深度分析，并按照分析结果制定基本解题思路。

（2）解题

按照解题思路以及在题目中获取的信息，逐步进行解题，进而完成解题任务。在此过程中，学生需要保证解题严谨性以及科学性，不仅要细致、严谨实施书写，同时还要保证整体思路表达完整程度。

（3）证明、检查

要在完成解答后，对整体解题过程展开检查，确定是否有遗漏或算错问题，并要及时对问题展开处理。老师应训练学生养成检查习惯，要在完成习题解答后，及时对解答过程展开逐一审核，确定自身解题思路是否合理，且最终解题答案是否准确等。要真正做到仔细检查，有理有据。

2.具体解题策略

（1）联想法

在利用联想法进行证明题解题时，并不是随意进行联想，而是要按照命题结果、特点，图形性质等，具体展开分析与研究，进而按照研究结果有目的的展开联想。在证明题解题中，联想法应用主要分为方法联想、定理和定义联想两种。

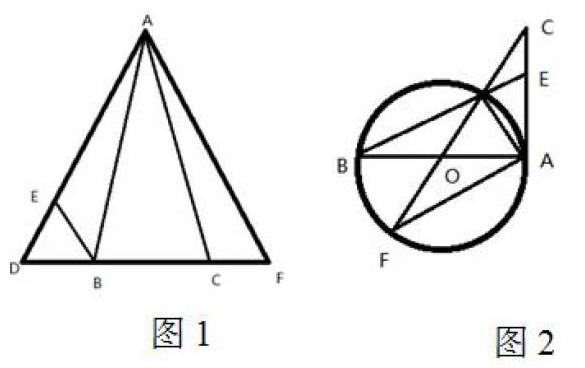
以人教版某证明题习题为例。例1：如图1所示，在△ABC中，AC=AB，D为CB延长线上一点，其中∠ADB=60°。同时得知，E为AD线上一点，且DB=DE。求证AE=BE+BC。

在运用联想法进行此题解答时，可通过添加輔助线的方式，进一步加深已知条件与求证结论之间的关系，进而帮助解题者理清整体解题思路，高质量完成解题任务。通过分析发现，想要证明结论，最为简单的方式，就是将两条线转移到一起，获得两条线段之和，之后再证明相等关系即可。所以可通过添加辅助线的方式，在图中完成全等三角形构建，进而完成相应证明。具体思路如下：延长DC到F，使CF=BD，再连接AF，易证△ABD≌△ACF得出AD=AF，又∠ADB=60?得△ADF是等边三角形，∴AD=DF，AD=AE+DE，DF=DB+BC+CF，又DE=DB，且∠ADB=60?，△DEB也是等边三角形。∴DE=BE=DB=CF，AE+DE=BE+BC+DE，因此，AE=BE+BC.

与普通解题方式相比，联想解题法更加锻炼学生解题思维，强调学生需要具备牢固的知识积累以及解题技巧，要从不同角度对题目已知条件进行运用，通过训练可对学生创新思维、反向解题等多项思维形成有效锻炼，会对学生数学学科综合素养提升，起到良好助力。

（2）分析法

数学证明题解题思路较为丰富，并不单一，不仅有正向思维、逆向思想解题法，同时也有正逆向思维结合解题法，学生在选择解题思维时，需要按照题目具体要求以及所提供条件，确定最终解题思维模式。其中正向思维主要以从前到后求证解题思路为主，是证明题基本解题思路，而逆向思维是从结论入手，按照结果对所需条件进行反向分析的解题方式。在运用分析法进行解题时，会假设命题为真，并对其为真原因展开分析，进而完成命题成立条件探索，属于逆向思维推理，是利用结论向已知条件进行靠拢的。

（3）正逆向思维结合法

正逆向思维是正向思维与逆向思维的有机结合，多用于高难度题目解答，极为注重解题思路。在结论无法完整推出解题思路，无法找到解题突破口时，可运用正逆结合思维进行解题。

例2：如图2所示，AB是圆O的直径，AC与圆切于点A，AC与AB长度相同。CO与圆交点为P，CO延长线与圆交点为F，AC与BP延长线交点为E，连接AF、AP。求证：CP=AE。

此题具有一定难度，在刚接触时，学生并不知道从何处下手，此时便可引导学生运用正逆向思维展开分析。为证明AE与CP相等，可运用等量代换思维进行解题，应以△ACP、△PCE关系分析为突破口，对相似关系展开证明，进而获得AC：AP=PC：PE的结论，之后只需证明△ABP、△EAP也存在相似关系即可。通过对正逆向思维的运用，学生可以快速按照已知条件完成结论推论，会将原来较为复杂的条件关系，清晰呈现在学生面前，帮助其完成一系列解题操作。

由于初中阶段数学难度与小学阶段难度存在一定差异，按照学生实际情况对学生展开证明题解题策略讲解，确保其可以真正掌握证明题解题思路以及解题技巧，能够真正做到以点概面，进而不断提升学生解题能力，保证学生数学课程学习质量。

参考文献

[1]秦振.初中数学开放探究题的类型及解题策略[J].中国数学教育，2019.195（05）：62-66

[2]冯建熹.谈初中数学几何推理与图形证明的解题策略[J].考试周刊，2018（43）：71-71

[3]葛敏洁.初中数学几何证明解题思路探析—以人教版初中数学为例[J].数学教学通讯，2018