影响民族院校统计学专业回归分析成绩因素的研究

李秀文 于海洋 刘力军

摘  要：学习成绩是评价学生素质的重要方面，也是教师检验教学能力、反思教学成果的重要标准。利用大连民族大学统计学专业本科生有关数据（专业基础课成绩、平时成绩和回归分析期末成绩），建立多元線性回归模型，对影响回归分析期末成绩的因素进行深入研究，其结果对今后的教学方法改进和教学质量提高具有十分重要的指导意义。

关键词：多元线性回归;专业基础课成绩;平时成绩;期末成绩

中图分类号：G640       文献标志码：A         文章编号：2096-000X（2020）16-0073-03

Abstract： Academic performance is an important aspect of evaluating students' quality， and it is also an important criterion for teachers to test teaching ability and reflect on teaching achievements. Based on the data of undergraduates majoring in statistics in Dalian Minzu University （specialized basic course scores， usual performance and regression analysis of final grades）， a multiple linear regression model was established to analyze the factors affecting the final grade of regression analysis. The results are very important for the improvement of teaching methods and the improvement of teaching quality in the future.

Keywords： multiple linear regression; specialized basic course scores; usual performance; final grades

为了实现教学目标，提高教学质量，有效提高学生学习成绩是很有必要的。我们知道专业基础课成绩必定影响专业课成绩，而且平时成绩也会影响专业课成绩，这两类成绩与专业课成绩基本上是呈正相关的，但它们之间的关系密切程度有多大？它们之间又存在怎样的内在联系呢？就这些问题，本文主要选取了2016级统计专业50名学生的四门专业基础课成绩以及回归分析的平时成绩和期末成绩，运用SPSS统计软件进行分析研究， 寻求回归分析期末成绩影响因素的变化规律，拟合出关系式，从而为强化学生的后续学习和提高老师的教学质量提供了有利依据。

一、数据选取

回归分析是统计专业必修课，也是统计学中的一个非常重要的分支，它在自然科学、管理科学和社会、经济等领域应用十分广泛。因此研究影响统计学专业回归分析成绩的相关性是十分重要的。

选取了统计专业50名学生的专业基础课成绩（包括数学分析、高等代数、解析几何和概率论）、回归分析的平时成绩和期末成绩，结合多元线性回归的基础理论知识[1-2]，建立多元回归方程，进行深入研究，可以直观、高效、科学地分析各种因素对回归分析期末成绩造成的影响。

二、建立多元线性回归模型1及数据分析

运用SPSS统计软件对回归分析期末成绩的影响因素进行研究，可以得到准确、科学合理的数据结果，全面分析评价学生考试成绩，对教师以后的教学工作和学生的学习会有较大帮助。自变量x1表示数学分析成绩，x2表示高等代数成绩，x3表示解析几何成绩，x4表示概率论成绩，x5表示平时成绩;因变量y1表示回归分析期末成绩，根据经验可知因变量y1和自变量xi，i=1，2，3，4，5之间大致成线性关系，可建立线性回归模型：

（1）

线性回归模型通常满足以下几个基本假设，

1. 随机误差项具有零均值和等方差，即

（2）

这个假定通常称为高斯-马尔柯夫条件。

2. 正态分布假定条件

由多元正态分布的性质和上述假定可知，随机变量y1 服从n维正态分布。

从表1描述性统计表中可看到各变量的平均值1=79.68，2=74.66，3=77.22，4=78.10，5=81.04，1=75.48;xi的标准差分别为10.847，11.531，8.929，9.018，9.221，y1的标准差为8.141;有效样本量n=50。

回归分析期末成绩y1的多元回归模型1为：

y1=-5.254+0.221x1-0.4x2+0.154x3

+0.334x4+0.347x5

从表2中可以看到各变量的|t|值，在给定显著水平？琢=0.05的情况下，通过t分布表可以查出，自由度为44的临界值t？琢/2（44）=2.015，由于高等代数x2的|t|值为0.651小于t？琢/2（44），因此x2对y1的影响不显著，其他自变量对y1都是线性显著的。下面利用后退法[3]剔除自变量x2。

三、后退法建立多元线性回归模型2及数据分析

从模型1中剔除了x2变量，多元回归模型2为：

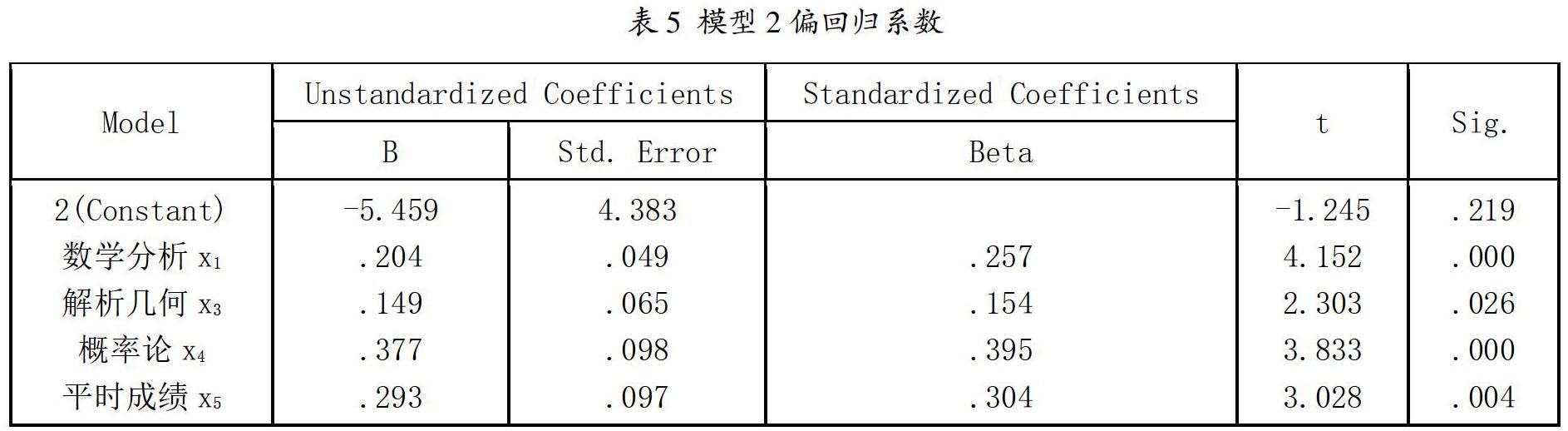
y1=-5.459+0.204x1+0.149x3+0.377x4+0.293x5（5）

在表4中，F统计量为90.326，在给定显著水平？琢=0.05的情况下，查F分布表可得，自由度為p=4和n-p-1=45的临界值F0.05（4，45）=2.579，所以F>F0.05（4，45），在表5中，所有自变量的|t|值都大于t？琢/2（45）=2.014，因此，多元回归模型2的线性关系是显著的。

四、结束语

通过对上述模型进行分析，即各个自变量对因变量的边际影响，可以得到以下结论：在保持其他条件不变的情况下，当数学分析成绩提高一分，则回归分析成绩可提高0.242分[4-5];同理，当解析几何成绩、概率论成绩和平时成绩每提高一分，则回归分析成绩分别提高0.149分、0.377分和0.293分。

通过对学生专业基础课成绩、平时成绩与回归分析期末成绩之间相关关系的研究，一方面有利于教师把控回归分析教学课堂，提高教师意识，注重专业基础课教学的重要性，同时，当学生平时成绩不好时，随时调整教学进度提高学生平时学习能力;另一方面使学生认识到，为了更好地掌握回归分析知识，应加强专业基础课的学习，提高平时学习的积极性。因此，通过对回归分析期末成绩影响因素的研究能有效的解决教师教学和学生学习中的许多问题。

参考文献：

[1]何晓群.应用回归分析（第四版）[M].北京：中国人民大学出版社，2015.

[2]任升录.关于线性回归模型的显著性检验[J].数学教学，2012（3）：7-8.

[3]李娜，王磊.后退法在MATLAB和SPSS中的实现[J].长春师范学院学报（自然科学版），2012，31（6）：31-34.

[4]王华丽.多元线性回归分析实例分析[J].科技资讯，2014（29）：22+24.

[5]张宇山.多元线性回归分析的实例研究[J].科技信息，2009（9）：54-56.

基金项目：辽宁省自然基金指导计划项目“基于传感器网络的空间区域场重构方法研究”（编号：2019-ZD-0169）

作者简介：李秀文（1984-），女，汉族，辽宁辽阳人，博士，讲师，研究方向：计算数学、统计学。

通讯作者：于海洋（1983-），男，汉族，辽宁辽中人，博士，讲师，研究方向：统计学，最优控制。