变风载下风电齿轮箱内部激励规律研究及动态特性优化
汤 亮,何仁杰,龚发云,李飞扬,刘冠军,杨 敏
(1.湖北工业大学机械工程学院,湖北武汉430070;2.湖北省制造业创新方法与应用工程技术研究中心,湖北武汉430070)
随着能源紧缺问题日益严峻以及风电技术高速发展,提高转换效率、降低故障率和改善振动与噪声已成为风电技术研究领域的重点。风电齿轮箱作为风电机组的核心部件,其传动性能决定了整个风电机组的运行质量。因受到变风载引起的外部激励及齿轮啮合形成的内部激励的影响,风电齿轮箱传动系统产生巨大的振动与噪声,加速了齿轮箱各零部件的疲劳损坏,造成一定的经济损失。因此,对风电齿轮箱进行振动与噪声的优化已成为一项重要研究。
为实现风电齿轮箱振动与噪声优化,国内外许多学者已开展了相关研究,如:Guan等[1]基于所建立的齿轮传动有限元模型,模拟了传动系统的误差激励,并测得系统在此激励下的振动响应;Zhao等[2]建立了由两级行星轮系与一级斜齿轮副结构组成的风电齿轮箱的振动模型,并分析了在齿轮传动误差及啮合刚度的影响下,风电齿轮箱动态特性的变化情况;Carbonelli等[3]从齿轮啮合刚度和传动误差两方面探究了齿轮箱辐射噪声的形成原因,并基于齿轮修形技术优化了齿轮箱的内部激励,改善和减小了其动态响应及噪声;Switonski等[4]优化了齿轮宏观参数,通过集中参数动力优化模型得到传动齿轮的最小振动幅值;刘华朝等[5]通过齿轮齿向及齿廓修形的方式改善了其内部激励,并分析了风电齿轮箱传动系统输出端响应加速度及噪声的变化情况;方源等[6]通过实验测试法研究了减速器的动态性能,为改善其啸叫噪声,基于多目标优化遗传算法,确定了齿轮最佳修形值,并运用边界元法分析了减速器辐射噪声的变化情况;张霖霖等[7]根据所建立的齿轮传动纯扭转动力学模型,研究了齿轮模数、齿数、螺旋角等宏观参数对齿轮动态特性的影响规律,并通过Kato 公式预估了齿轮的辐射噪声;陈思雨等[8]以齿轮副振动幅度作为衡量齿轮修形优劣的指标,在较大转速范围内研究了齿轮修形对齿轮传动动态特性的影响。
从以上文献分析可知,针对风电齿轮箱振动与噪声优化问题,现有手段主要是通过齿轮修形来改善齿轮啮合的内部激励,从而实现齿轮箱传动系统的减振降噪。但是,上述研究均在单一工况下确定齿轮修形量,而载荷、转速等工况参数改变后,该修形量未必适用,且运用齿轮宏观参数优化法来改善风电齿轮箱振动与噪声的研究还较少。对此,笔者在建立风电齿轮箱动力学模型的基础上,对多工况下风电齿轮箱传动系统进行动力学仿真分析,应用遗传算法寻求齿轮的最优修形量,使它在一定工况范围内有较好的适用性;通过对基本齿条刀具的优化,以修改齿顶厚度、齿顶高度及齿根高度的宏观参数优化法来增大齿轮重合度,并结合最优齿轮修形量来提升风电齿轮箱的动力学特性,以改善其振动及噪声。
1 风电齿轮箱动力学模型构建及风载工况模拟
1.1 风电齿轮箱传动系统
以某型号兆瓦级风电齿轮箱为研究对象,其传动系统由两级行星轮系及三级斜齿轮副组成,通过Romax Designer软件建立风电齿轮箱传动系统三维模型,如图1所示。外部转矩经一级行星轮系的行星架输入、太阳轮输出后,传递至二级行星轮系,二级太阳轮将转矩传递至三级斜齿轮副输入轴,最终由输出轴输出,以达到增速的效果。风电齿轮箱传动系统各级齿轮副的基本参数如表1所示。

图1 风电齿轮箱传动系统结构简图及三维模型Fig.1 Structure diagram and three-dimensional model of wind turbine gearbox transmission system
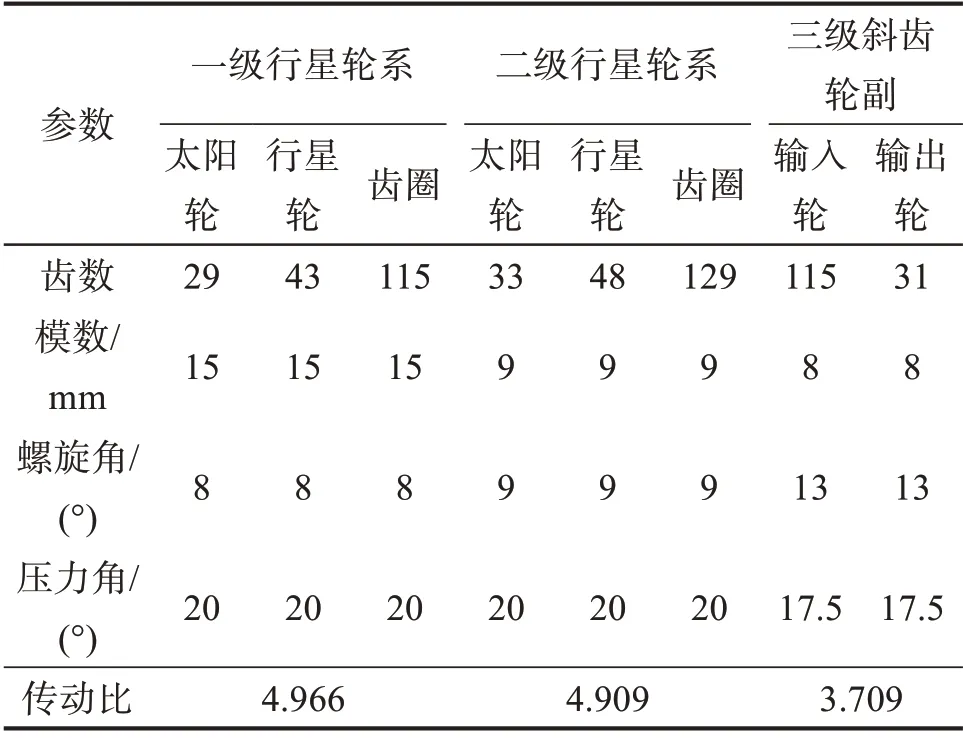
表1 风电齿轮箱传动系统各级齿轮副的基本参数Table 1 Basic parameters of gear pairs in wind turbine gearbox transmission system
1.2 风电齿轮箱刚柔耦合动力学模型
考虑到箱体、行星架等部件的结构柔性,建立箱体及行星架等部件的有限元模型后,采用节点连接方式将各部件有限元模型与传动系统三维模型耦合起来,并在箱体扭力臂处施加约束,以模拟机架对箱体的支撑作用。风电齿轮箱刚柔耦合动力学模型如图2所示。

图2 风电齿轮箱刚柔耦合动力学模型Fig.2 Rigid-flexible coupled dynamics model of wind turbine gearbox
图3 为风电齿轮箱传动系统动力学模型,图中Ksi、Kpi、Kri、Kci、Kgη和Csi、Cpi、Cri、Cci、Cgη分别表示太阳轮、行星轮、齿圈、行星架、三级齿轮的耦合支撑刚度和阻尼,Kpiri、Cpiri分别表示行星轮-齿圈的啮合刚度和啮合阻尼,其中i=1,2,η=3,4。
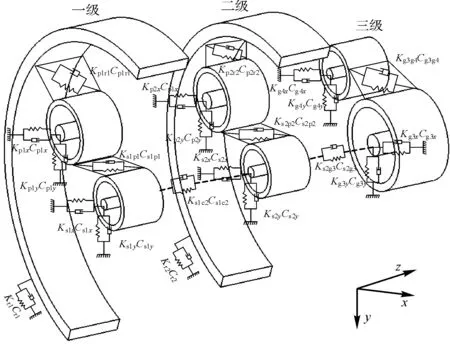
图3 风电齿轮箱传动系统动力学模型Fig.3 Dynamics model of wind turbine gearbox transmission system
在风电齿轮箱传动系统各支撑部位建立耦合节点,将轴承、齿圈等部件的支撑刚度及阻尼与箱体有限元模型相耦合,确立耦合支撑刚度和阻尼后,计算各齿轮激励下风电齿轮箱的动态响应。风电齿轮箱刚柔耦合动力学方程为:
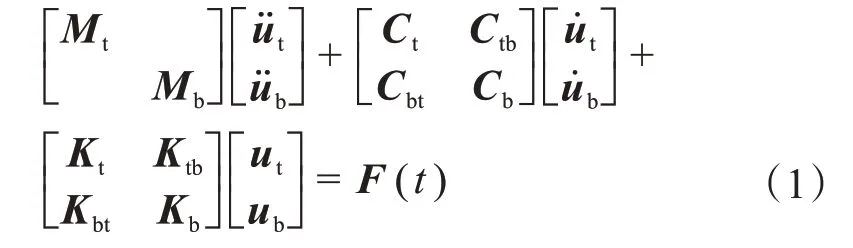
式中:Mt(Mb)为传动系统(箱体)质量矩阵;Ct(Cb)为广义传动系统(箱体)阻尼矩阵;Ctb(Cbt)为广义传动系统(箱体)耦合阻尼矩阵;Kt(Kb)为广义传动系统(箱体)刚度矩阵;Ktb(Kbt)为广义传动系统(箱体)耦合刚度矩阵;u¨t、u˙t、ut(u¨b、u˙b、ub)分别为传动系统(箱体)的加速度、速度、位移向量;F(t)为系统内部动态激励。
1.3 风电齿轮箱外部变风载工况
依据风电机组某一运行周期内的实测风载数据及空气动力学公式[9],计算风电齿轮箱传动系统的输入转矩。为便于分析变风载下兆瓦级风电齿轮箱的动态特性,对载荷持续总时间进行归一化处理,并将输入转矩曲线近似离散成10 种不同的转矩工况(L01,L02,…,L10),如图4所示。
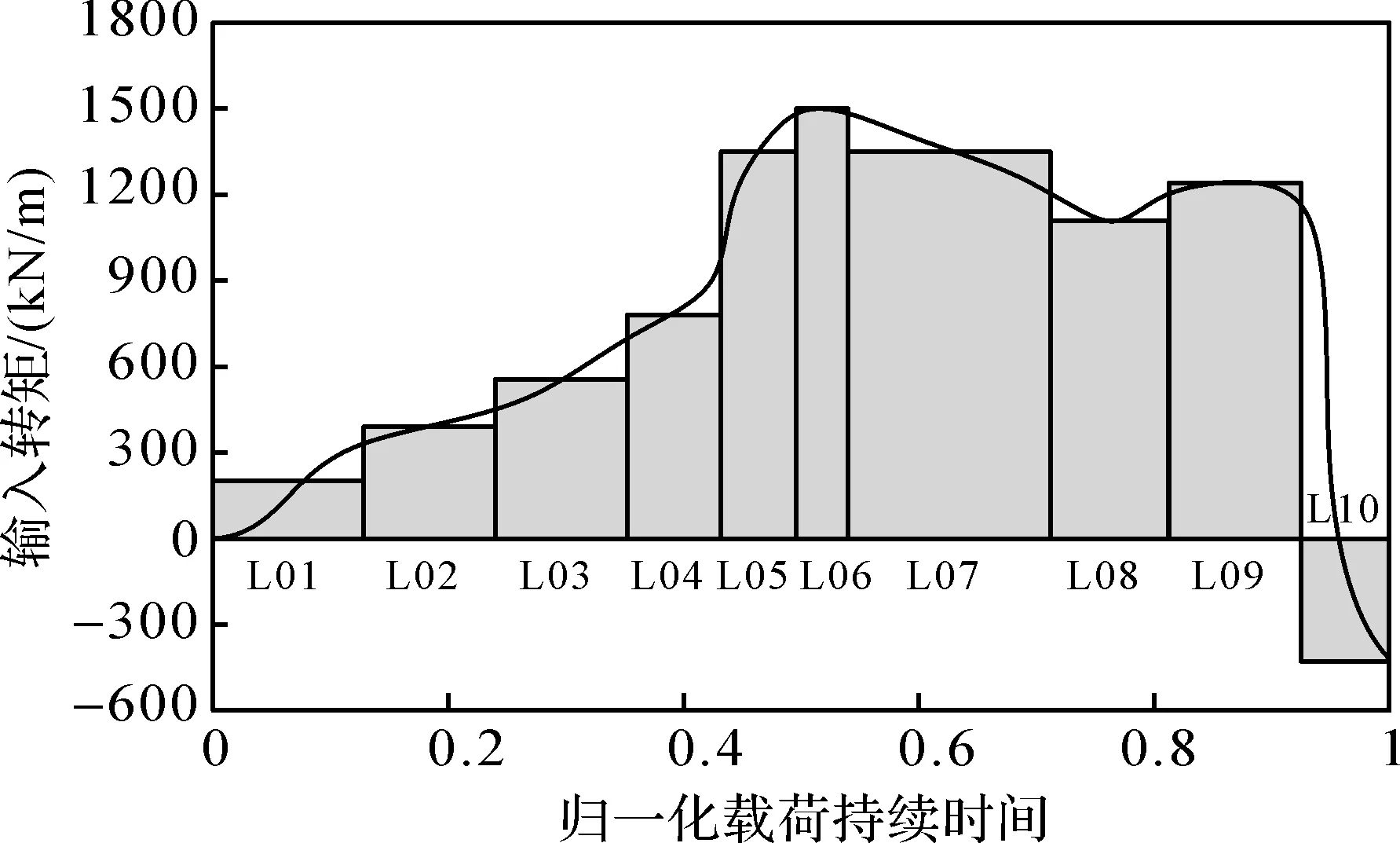
图4 某一运行周期内风电齿轮箱传动系统输入转矩Fig.4 Input torque of wind turbine gearbox transmission system in a certain operating cycle
2 变风载工况下风电齿轮箱传动特性及响应分析
2.1 齿轮内部激励
在齿轮传动系统中,齿轮传动误差与啮合刚度激励是系统内部激励的重要组成部分,亦是衡量系统振动与噪声的关键指标[10-11]。
图5(a)为10种工况下各级齿轮的传动误差值,可以看出,随着工况的转变,一级齿圈的传动误差曲线出现了较大起伏。L06工况下一级齿圈的传动误差如图5(b)所示,其传动误差值(沿啮合线位移的上下差值)达到最大值,为15.92 μm。一级太阳轮和二级齿圈的传动误差曲线的起伏趋势次之,三级输出轮及二级太阳轮的传动误差曲线较为平稳,几乎未受到工况转变的影响。由此可见,部分齿轮的传动误差受工况转变的影响较大。
图6所示为L06工况下三级斜齿轮的啮合刚度,对于斜齿轮,综合啮合刚度的波动量即代表齿轮啮合刚度激励。
图7为各级齿轮啮合刚度激励随工况的变化曲线。行星架等部件的受载变形使各齿轮产生了偏心误差,进而改变了齿轮总接触线长度的变化范围,造成啮合刚度激励发生变化[12]。由图可以看出:一级、二级太阳轮的啮合刚度激励在前9个工况下均未变化,但在L10工况下均发生突变;其它齿轮的啮合刚度激励在不同工况下有较大变化。
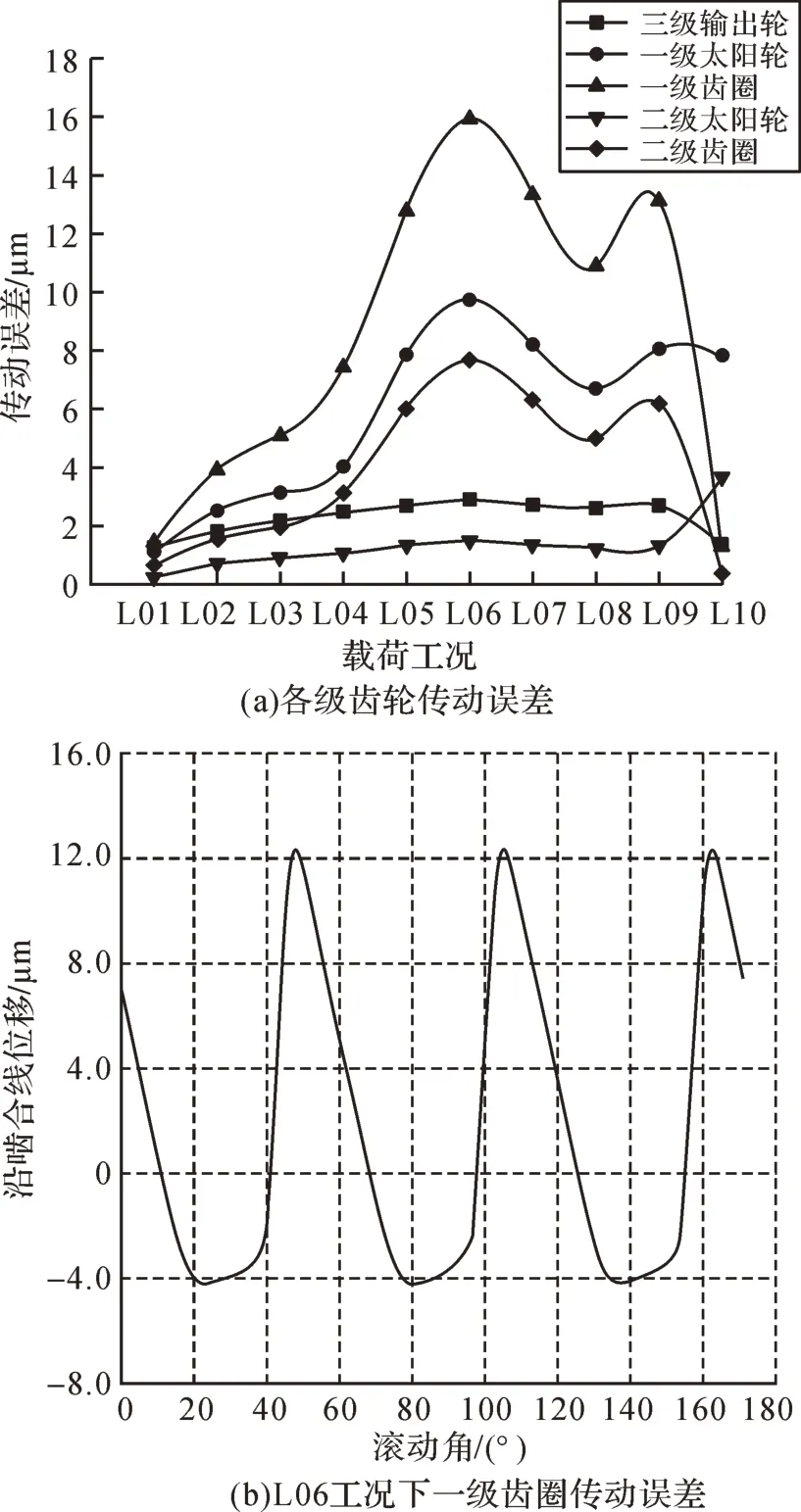
图5 变风载工况下各级齿轮的传动误差Fig.5 Transmission error of gears under varying wind load condition
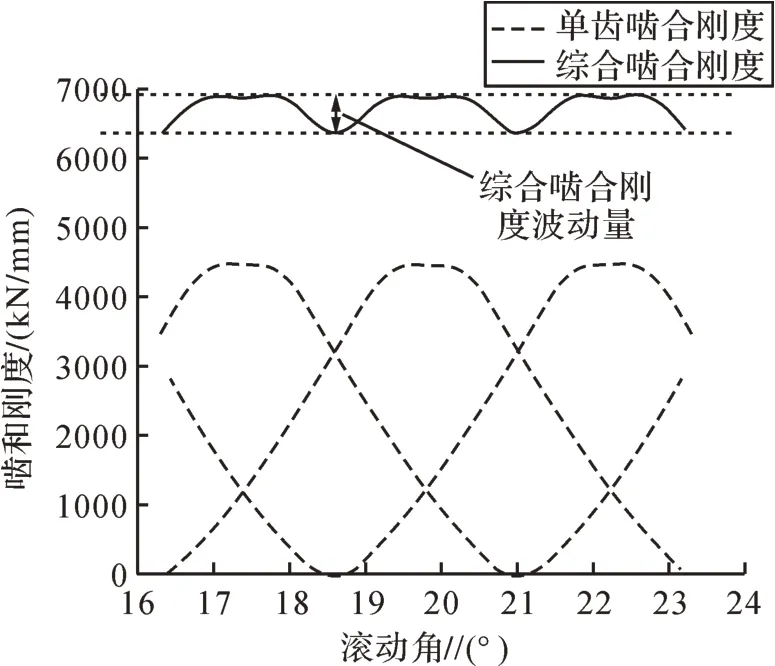
图6 L06工况下三级斜齿轮啮合刚度Fig.6 Meshing stiffness of third stage helical gear under L06 working condition
2.2 风电齿轮箱振动加速度分析
在齿轮内部激励的影响下,风电齿轮箱三级下风向轴承座的振动能量最大[5]。因此,对齿轮箱三级输入输出轴轴承座进行振动加速度分析。如图8所示,布置测点以检测轴承座特定位置的振动加速度,其中:测点1用于输出轴轴承座的加速度检测,测点2用于输入轴轴承座的加速度检测。

图7 变风载工况下各级齿轮的啮合刚度激励Fig.7 Meshing stiffness excitation of gears under varying wind load condition

图8 风电齿轮箱上测点布置Fig.8 Arrangement of measuring points on wind turbine gearbox
图9为三级输入输出轴轴承座振动加速度随工况的变化曲线。由图可知,输出轴轴承座的振动加速度明显大于输入轴轴承座,且在L05工况下两轴承座的振动加速度均达到最大,分别为6.72 和3.91 m/s2。

图9 风电齿轮箱三级输入输出轴轴承座振动加速度Fig.9 Vibration acceleration at third stage input and output shaft bearing seat of wind turbine gearbox
3 风电齿轮箱各级齿轮副优化
3.1 各级齿轮副宏观优化
齿轮传动的动态特性受其重合度的影响较大:重合度越高,齿轮传动振动越小,且啮合越平稳,噪声越小[13-14]。以齿轮重合度为优化目标,以齿顶高度、齿根高度和齿顶厚度为设计变量,以齿顶间隙、根切间隙及齿条刀尖圆角半径为约束条件,对风电齿轮箱各级齿轮副的宏观参数进行优化。因优化过程中齿轮重合度的增大将导致齿顶厚度减小,从而显著减小齿轮的弯曲强度,依据相关标准,为满足齿轮弯曲强度要求,规定齿顶厚度/模数>0.3[15]。
依据齿轮重合度公式[16]对风电齿轮箱各级齿轮副的重合度进行计算,其中式(2)用于计算行星轮系外啮合齿轮的端面重合度,式(3)用于计算行星轮系内啮合齿轮的端面重合度,式(4)用于计算三级斜齿轮副的端面重合度,式(5)用于换算齿轮齿顶压力角与全齿高。

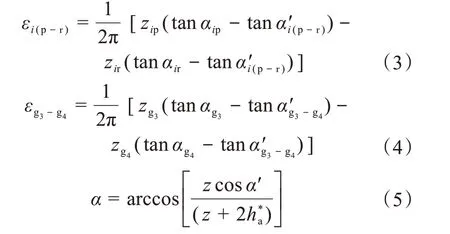
式中:εi(s-p),εi(p-r),εg3-g4分别为第i级(i=1,2)行星轮系的太阳轮-行星轮、行星轮-齿圈及三级斜齿轮副的端面重合度;zis,zip,zir,zg3,zg4分别为第i级行星轮系太阳轮、行星轮、齿圈及三级输入输出轮的齿数;αis,αip,αir,αg3,αg4分别为第i级行星轮系太阳轮、行星轮、齿圈及三级输入输出轮的齿顶圆压力角;α'i(s-p),α'i(p-r),α'g3-g4分别为第i级行星轮系太阳轮-行星轮、行星轮-齿圈及三级斜齿轮副的啮合角;α包括αis,αip,αir,αg3,αg4,α′包括α'i(s-p),α'i(p-r),α'g3-g4,z包括zis,zip,zir,zg3;为齿顶高系数。
通过增大齿轮副端面重合度,可增大齿轮副总重合度。优化前后风电齿轮箱各级齿轮副的宏观参数和重合度如表2所示。

表2 优化前后各级齿轮副的宏观参数和重合度Table 2 Macro-parameters and contact ratio of gear pairs before and after optimization
由表2可知,风电齿轮箱各级齿轮副的宏观参数优化后,各级齿轮副的端面重合度及总重合度都得到了有效的提升。尽管优化造成齿顶厚度有一定削减,但仍满足齿顶厚度/模数>0.3的规定,在一定程度上保证了齿轮的弯曲强度。
3.2 各级齿轮副微观优化
齿轮宏观参数优化后,风电齿轮箱的传动特性已得到一定程度的改善。但由时变风载引起的各部件的变形会导致风电齿轮箱各齿轮副仍有较大内部激励及偏载。
齿轮修形是减小齿轮内部激励及改善齿轮振动与噪声的有效方法。由上文分析可知,齿轮传动误差及啮合刚度受工况转变的影响较大,若仅针对单一工况确立修形量,则在其它工况下,该修形量未必适用。因此,需寻得一组在多工况下均能达到理想效果的最优修形量。
遗传算法是一种全局优化搜索算法,具有强鲁棒性,可以解决复杂工况下齿轮修形量理论计算值存在偏差的问题,十分适用于齿轮修形设计研究[17]。
鉴于此,运用遗传算法对变风载工况下各级齿轮修形量进行寻优计算,以各级齿轮齿廓鼓形量Cb、齿廓斜度βb、齿向鼓形量Ca及齿向斜度βa为优化变量(如图10 所示,图中h、b分别表示全齿高度及齿宽),以各级齿轮在所有工况下的内部激励和σΣ最小为优化目标。在额定工况下运用齿轮修形经验公式确立各级齿轮优化变量的取值范围[18]。考虑到各工况运转周期不同,在计算齿轮内部激励和时应考虑各工况运转周期占载荷持续总时间的权重,计算公式为:

式中:kn为第n个工况的运转周期占载荷持续总时间的比值,σn为以某修形量(种群个体)修形优化后,齿轮在第n个工况下的内部激励。

图10 齿轮修形优化变量Fig.10 Gear modification optimization variables
设置遗传算法种群数为100,变异系数为0.3,交叉系数为0.2,适应比为0.1,迭代次数为20,对变风载工况下各级齿轮修形量进行寻优计算,具体寻优流程如图11所示。

图11 基于遗传算法的齿轮修形量寻优流程Fig.11 Optimizing process of gear modification amount based on genetic algorithm
以三级输出斜齿轮的齿向鼓形量寻优为例,通过图12所示的单一修形量下的优化点阵图可知,三级输出斜齿轮的内部激励和σ∑的最小值趋近于60。的各级齿轮的最优修形量代入Romax齿轮微观修形模块中,形成各级齿轮最优修形量云图,如图13 所示。由于风电齿轮箱运行时齿轮仅单向转动,故只对一侧齿面进行修形。

表4 风电齿轮箱各级齿轮的最优修形量Table 4 Optimum modification amount of gears in wind turbine gearbox 单位:µm
按上述流程对各级齿轮修形量寻优,得到风电齿轮箱各级齿轮的最优修形量,如表4所示。将所得
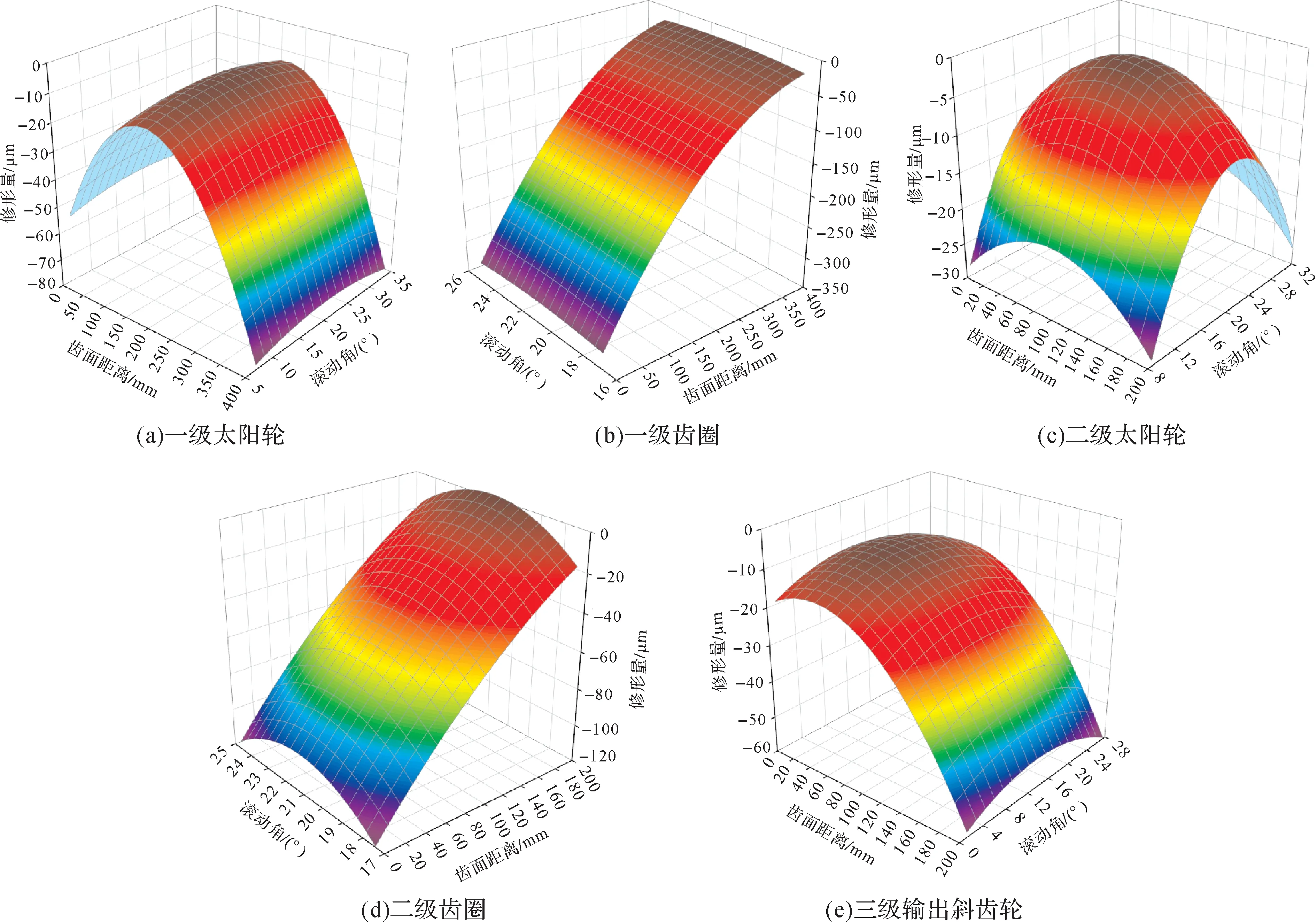
图13 风电齿轮箱各级齿轮最优修形量云图Fig.13 Nephogram of optimum modification amount of gears in wind turbine gearbox
4 变风载工况下优化后风电齿轮箱动态响应分析
4.1 优化后各级齿轮的传动误差
对优化后的风电齿轮箱各级齿轮进行传动误差分析,并与优化前的传动误差进行比较,结果如图14所示。
由图14可以看出:各级齿轮的传动误差显著减小;对比优化前,优化后各级齿轮的传动误差随工况转变的起伏明显平缓;在L06工况下,一级齿圈的传动误差由15.92 μm下降到了2.52 μm,改善了84.2%;但在某些工况下,该优化方法还存在不足,比如在L01、L02、L03工况下,一级齿圈的传动误差较优化前反而增大。不过从总体看,能取得多工况下的优化效果。

图14 优化前后各级齿轮传动误差对比Fig.14 Comparison of transmission errors of gears before and after optimization
4.2 优化后各级齿轮的啮合刚度激励
图15为优化前后风电齿轮箱各级齿轮啮合刚度激励的对比。
由图15可知:通过宏观参数优化和齿轮修形后,各工况下所有齿轮的啮合刚度激励均得到了有效改善;相对于传动误差的改善,各级齿轮啮合刚度激励的改善并未呈现不足。
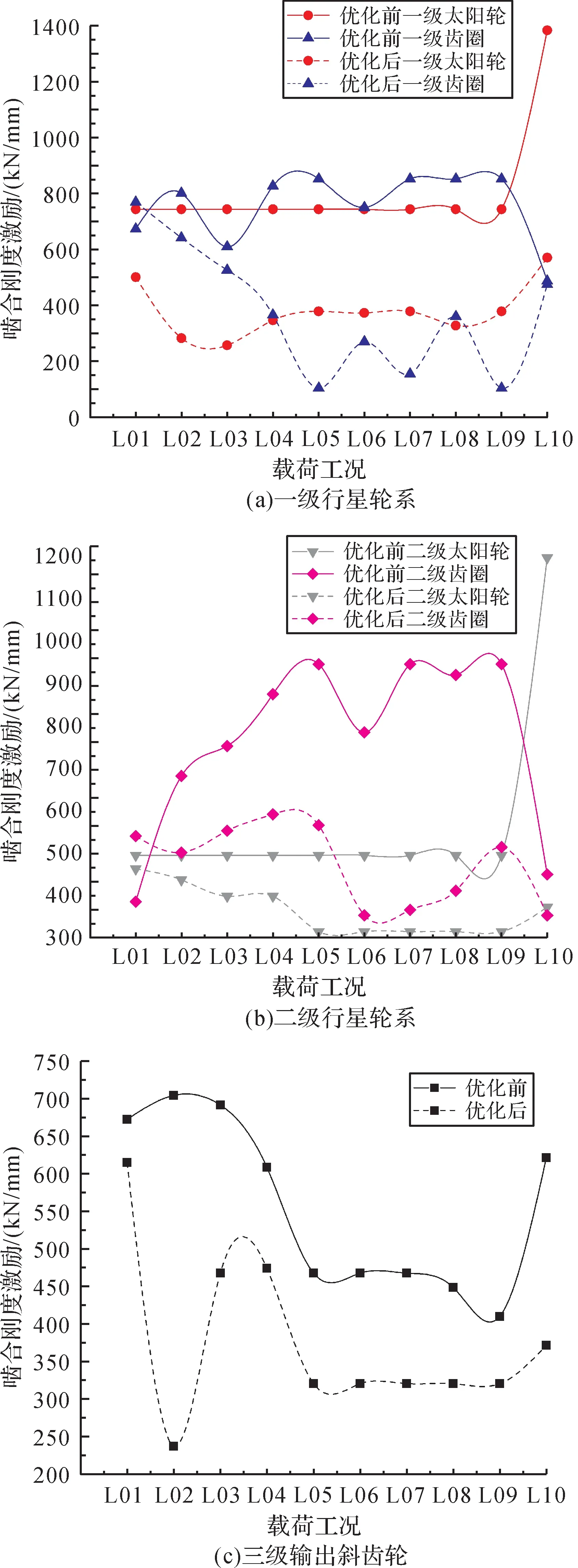
图15 优化前后各级齿轮啮合刚度激励对比Fig.15 Comparison of meshing stiffness excitation of gears before and after optimization
4.3 优化后三级输入输出轴轴承座振动加速度及噪声
对优化后风电齿轮箱的三级输入输出轴轴承座进行振动加速度分析,并根据振动加速度级公式(7)计算三级输入输出轴轴承座的结构噪声,结果如图16所示。
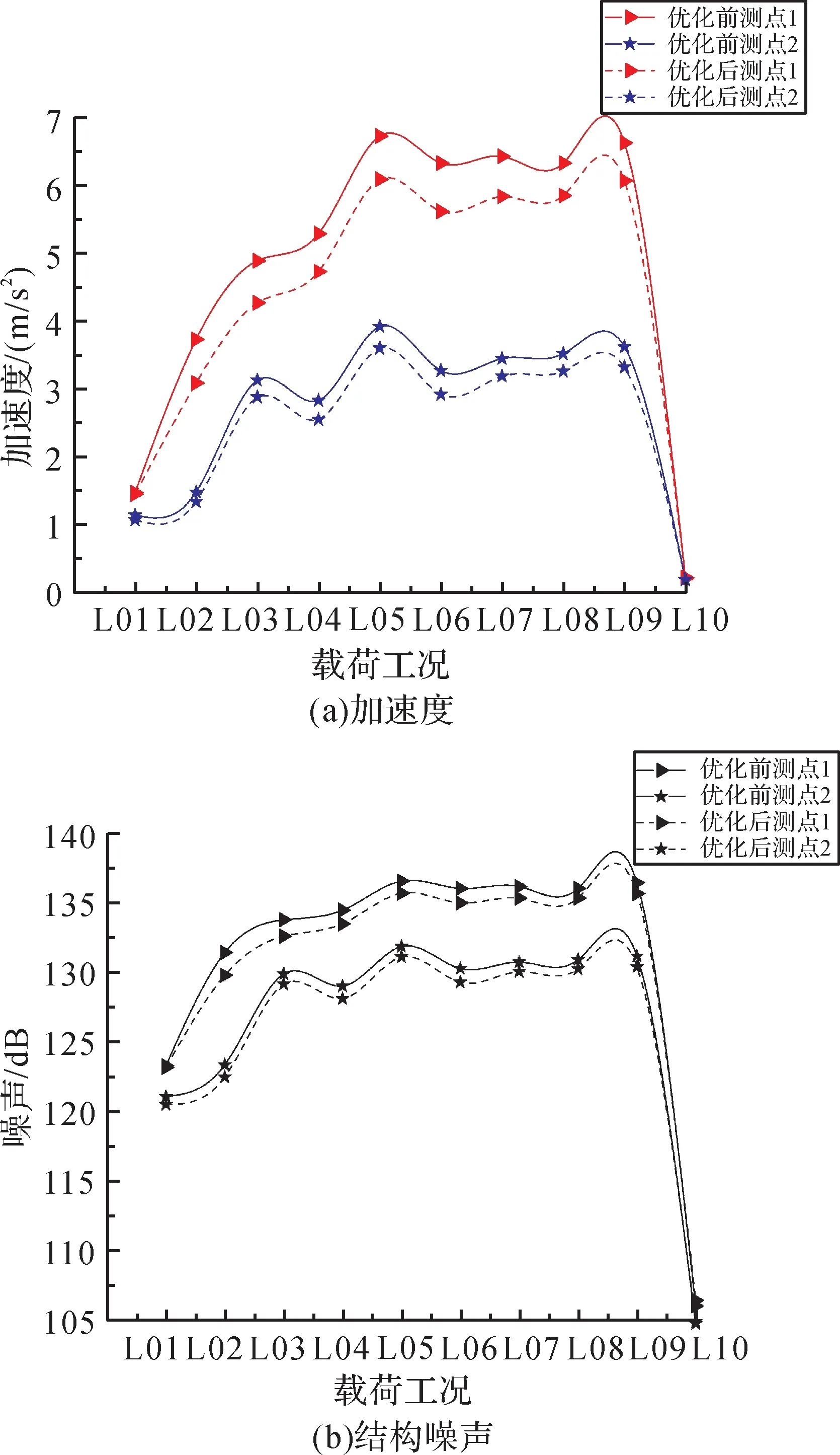
图16 优化前后三级输入输出轴轴承座振动加速度及结构噪声对比Fig.16 Comparison of vibration acceleration and structural noise of third stage input and output shaft bearing seat before and after optimization

式中:La为结构噪声,dB;a为轴承座加速度有效值,m/s2;a0为基准加速度,a0=1.00×10-6m/s2。
由图16可以看出,优化后,各工况下三级输入输出轴轴承座的振动加速度及结构噪声明显减小,且相比于输入轴轴承座,输出轴轴承座振动加速度及结构噪声的改善效果更为显著。以输出轴轴承座为例,优化前后各工况下其振动加速度及结构噪声分别如表5 和表6 所示。由表可知,L02 工况下输出轴轴承座振动加速度和结构噪声的改善效果最优,振动加速度减小了17.2%,结构噪声降低了1.7 dB。
5 结 论
1)以某型号兆瓦级风电齿轮箱为研究对象,考虑到箱体及行星架等部件的结构柔性,将各部件有限元模型与传动系统三维模型以节点连接方式耦合起来,建立风电齿轮箱刚柔耦合动力学模型,并通过空气动力学公式模拟了风电齿轮箱传动系统的输入转矩。
2)分析了变风载工况下风电齿轮箱齿轮内部激励变化规律,得出齿轮传动误差及啮合刚度激励受工况转变的影响较大;分析了齿轮内部激励下风电齿轮箱三级输入输出轴轴承座的振动加速度。
3)以齿轮修形量在多工况下有效为前提,以各级齿轮内部动态激励和最小为优化目标,基于遗传算法寻得适用于多工况的最优修形量,并与齿轮宏观参数优化方式相结合,改善变风载工况下风电齿轮箱的动态特性。
4)对比变风载工况下优化前后风电齿轮箱的动态特性,结果表明:该风电齿轮箱的振动加速度及结构噪声在各工况下均有明显改善,振动加速度最大减小了17.2%,噪声最大减小了1.7 dB。

表5 优化前后输出轴轴承座振动加速度对比Table 5 Comparison of vibration acceleration at output shaft bearing seat before and after optimization

表6 优化前后输出轴轴承座结构噪声对比Table 6 Comparison of structural noise at output shaft bearing seat before and after optimization 单位:dB

