基于改进有序聚类法的立式加工中心进给系统温测点优化
李传珍,李国龙,陶小会,庞 源
(重庆大学机械传动国家重点实验室,重庆400044)
随着智能制造的高速发展,智能化、高精度、高速化的数控机床已成为研发重点[1]。研究表明,在精密加工过程中因热变形引起的精度误差占总误差的40%~70%,因此热误差补偿是提高机床加工精度的关键[2-3]。热误差补偿的有效性受热误差预测模型精度的影响,目前建立精确热误差预测模型的难点之一是准确选取温测点。
针对温测点优化问题,国内外学者已通过有限元法[4]、神经网络[5-6]、AVQ(adaptive vector quantization,自适应矢量量化)聚类[7]、模糊聚类法[8]等实现了温测点优化,有效减少了温测点的数目,提高了热误差预测模型的精度和鲁棒性。但是,随着机床加工精度的提高,对热误差预测模型的精度要求也更高,基于传统单一理论的温测点优化方法已不能满足要求。为选取更加准确的温测点,张伟等[9]采用灰色关联分析和模糊聚类法实现了卧式加工中心温测点的优化;Miao等[10]利用模糊聚类法与灰色关联度分析获得了各类温测点的关键点,并采用逐步回归法剔除了非显著温测点,完成了高速加工中心主轴温度测点的优化;丛明等[11]提出了将简单相关分析、模糊聚类法、灰色关联度分析和热误差预测模型参数统计学分析相结合的温测点优化方法,并基于这种优化方法确定了卧式加工中心主轴的最佳温测点;李艳等[12]采用互信息法建立了温度变量与热误差的综合关联度矩阵,根据改进模糊聚类法对温测点进行分类,并结合综合关联度矩阵选取数控磨齿机主轴的关键温测点;李逢春等[13]提出一种兼顾欧式距离和相关系数的改进系统聚类法,有效解决了易干扰温度信号区分问题和温测点间共线问题,实现了重型落地铣镗床的温测点优化;魏弦等[14]采用模糊聚类法和相关性分析确定了龙门机床进给系统的关键温测点,并采用特征提取法获得热误差预测模型的自变量,有效消除了温测点间的复共线性,确定了最佳温测点。综合来看,目前基于多种理论的温测点优化方法主要涉及温测点共线性消除和温测点聚类等,其中:温测点共线性消除普遍使用逐步回归法和简单相关性分析等全局式筛选方法,但这些方法均未考虑温测点布置的疏密情况,对所有温度变量笼统地进行筛选,当温测点布置密集时,上述方法的筛选效果较差;温测点聚类大多采用模糊聚类法及其相关理论,但模糊聚类分析的阈值大多通过试验和经验获得,且在分类时只根据温测点温度样本的亲疏性质或距离而未考虑温度有序传递的特点,这会导致温测点优化后所建立的热误差预测模型的精度和鲁棒性较差。考虑到立式加工中心进给系统的有效进给行程较短,发热源较集中且温度有序传递,相较于其他机床,该加工中心具有不同的温度场分布,其温测点更密集,且温测点间的耦合效应也更显著,因此其温测点优化方法有待深入研究。
针对上述问题,笔者以三轴立式加工中心为研究对象,基于该机床进给系统的发热特点,提出一种基于改进有序聚类法的温测点优化方法。首先,该方法改变了传统温测点全局式初筛的方式,采用互信息值(即相关性)对机床进给系统各发热部件的多个温测点进行局部式初筛,不仅提高了温测点初筛精度,还有效消除了测点间的共线性。其次,基于机床进给系统温度有序传递的特点,对初筛后的温测点进行结合统计学检验的改进有序聚类分析,从而确定最佳温测点。最后,根据最佳温测点建立立式加工中心进给系统的热误差预测模型,并与基于传统有序聚类法和灰色关联度模糊聚类法建立的热误差预测模型进行比较,以验证利用本文方法建立的热误差模型具有更高的精度和鲁棒性。
1 基于改进有序聚类法的温测点优化方法
1.1 改进有序聚类法的提出
传统有序聚类法是:先通过计算类直径矩阵和误差函数,获得温测点分类;再计算误差函数曲线中变化较明显处相邻聚类数误差函数的比值,比值较大且通过显著性检验的聚类数为最佳聚类数;最后通过温度变量与热误差之间的简单相关性分析,选出关键温测点[15]。然而,相邻聚类数误差函数的比值仅反映了2个聚类点误差函数的大小关系,并不能准确反映误差函数曲线的变化值,且有序聚类法的聚类数一般在12个以下,较少的样本点受拟合曲线类型的影响较大,因此无法根据误差函数曲线斜率变化率确定最佳分类。此外,为消除温测点间的耦合性和共线性,一般先根据温度变量与热变形的相关性初步筛选温测点,再进行分类,这种全局式温测点初筛方法在温测点布置稀疏时效果较好,但当温测点布置密集时,此方法筛选效果较差,无法精确筛选出关键温测点。
立式加工中心属中小型数控机床,结构紧凑,进给行程较短,进给系统发热源集中且温度场分布有序;在热误差试验中温测点布置得十分密集。因此,结合立式加工中心进给系统的发热特点,根据互信息值针对性地初步筛选进给系统各发热部件不同位置的同类温测点,并针对原有序聚类法最佳聚类数难以确定的问题,提出一种基于多元线性回归,由F检验、t检验、判定系数相关性检验和残差比较等统计学分析确定最佳聚类数的改进有序聚类法,并利用该方法确定立式加工中心进给系统最佳温测点。
1.2 改进有序聚类法的步骤
针对布置了多个温测点的发热部件,先由互信息值初步筛选各温测点,计算初选温度变量的类直径矩阵和比较误差函数,获得初始分类;再结合统计学分析确定最佳聚类数和最佳温测点。具体步骤如下所述。
1)计算互信息值。
根据信息论产生的互信息法用信息熵来衡量2个序列变量的相关性[12]。以温测点温度变化量为温度样本,设立式加工中心进给系统温测点温度随时间的变化量ΔTi(t)=Ti(t)-T(0i表示温测点编号,i= 1,2,…,n),每个温测点有m个温度变量样本,则各温测点温度变量样本集合ΔTi={ΔTij(t)}(j= 1,2,…,m),其中ΔTij(t)表示第i个温测点的第j个温度变化量。丝杠热误差随时间的变化量Y(t)为该时刻丝杠测量终点热误差与丝杠测量起始点热误差之差,即Y(t)=Y终(t)-Y0(t),热误差样本集合Y=Yj(t)(j= 1,2,…,m),则各温测点温度变量ΔTi与热误差Y相关性的互信息值为:

式中:p(⋅)为概率密度函数,p( ΔTij,Yj)是ΔTi与Y的联合概率密度函数。
根据式(1)可计算得各温测点温度变量与热误差的互信息值I,I越大表示该温测点与热变形的相关性越大。根据相关性大小,对各部件不同位置的同类温测点(如在螺母上下端面、外壳、内圈布置4个温测点是为了更准确地获得螺母的发热位置,则这4个测点可归为螺母的同类测点)进行初步筛选,消除温测点间的耦合性。
2)数据规格化处理。
为消除不同数据类型间的差异,降低计算误差,将温测点温度变量样本矩阵X中的元素xab变换为zab,获得有序样本矩阵Z,变换公式为:

式中:xab表示温测点初筛后第b个原始样本的第a个温测点温度变化值;a= 1,2,…,l;b= 1,2,…,m。
3)计算类直径矩阵D。
有序聚类法采用直径表示类中的差异程度,类中差异越小,直径就越小,类中样本就越集中[15]。设有序聚类样本中的一个类为{za,za+1,…,zc} (a<c≤l),用D(za,zc)表示该类的类直径,D(za,zc)可用离差平方和表示为:

式中:za为正规化处理后第a个温测点的温度变化值,为第a个到第c个温测点温度变化值的均值,即
4)计算误差函数。
将l个温测点分成k类,各类的误差函数可表示为各类的直径之和,将温度样本简记为f,q(k,l)为l个温测点分成k类的一种分法,则误差函数ψ[q(k,l)]为:
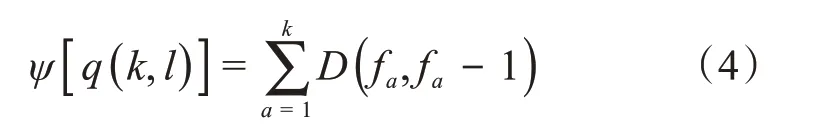
式中:D(fa,fa- 1 )表示某一子类的离差平方和。
当n和l固定时,ψ[q(k,l)]越小,表示各类的类直径越小,分类越合理[15]。因此,有序聚类法的最优分类就是选择一种分法使得ψ[q(k,l)]最小。
5)确定最优分法。
当k=2时,q( 2,l)是所有可能的分类中使误差函数最小的分法[15],故有:

对上式进行归纳,即有:

首先寻找合适的a值,使得ψ[q(k,l)]=ψ[q(k-1,fk-1)]+D(fk,fl) 最 小,得 到 第k类Gk={fk,fk+1,…,fl};接着寻找fk-1,使得ψ[q(k-1,fk-1)]最小,其中
ψ[q(k-1,fk-1)]=ψ[q(k-2,fk-1-1)]+D(fk-1,fk-1),得到第k-1 类Gk-1={fk-1,fk-1+1,…,fk-1};依此类推可得到所有的分类G1,G2,…,Gk。
6)确定最佳聚类数。
首先绘制误差函数随聚类数k变化的误差函数曲线,选取该曲线明显变化处的聚类数作为温测点数目,然后结合各温测点的互信息值选取建模所用的温测点,建立包含多个不同温测点的热误差多元线性回归模型。对模型先进行F检验,判断热误差模型的显著性;再分析其线性相关性系数R2和最大残差,R2越大,表明该模型的拟合效果越好,最大残差值越小,表明该模型的精度越高;最后对回归系数进行显著度t检验,剔除不显著的温测点,进而确定最佳聚类数和最佳温测点。
1.3 基于改进有序聚类法的温测点优化流程
根据采集的机床进给系统温测点的温度和热变形数据,基于改进有序聚类法确定最佳温测点,总体流程如图1所示。

图1 基于改进有序聚类法的温测点优化流程Fig.1 Optimizing process of temperature measurement points based on improved sequential clustering method
2 温测点优化试验
2.1 立式加工中心进给系统热源分析
不同数控机床因结构、工作转速(进给速度)、有效进给行程存在差异,其温度场分布不同,则热误差建模选取的关键温测点也不同[2]。文献[14,16-17]分别对龙门加工中心、镗床和立式加工中心的进给系统进行研究后发现:龙门加工中心各热源温度曲线上升趋势不同且热平衡时各热源温度差较大,镗床各热源温度曲线上升趋势相似但热平衡时各热源温度差明显,立式加工中心各热源温度曲线分布密集、上升趋势相似且热平衡时各热源温度差较小,由此可见不同数控机床发热规律差别较大,温测点的布置也不同。因此,考虑到立式加工中心进给系统结构紧凑,进给行程较短,发热源集中且温度场分布有序的特点,根据文献[17-18]中的立式加工中心进给系统热源分析,确定其温测点布置位置为电机、联轴器、上下轴承盖和螺母内外圈。
2.2 温度与热变形样本采集试验
本文的试验对象为华中八型立式加工中心VMC850,采集其进给系统(以Z向为例)的温测点温度与热变形数据。根据2.1节的热源分析,在该立式加工中心Z向进给系统的电机、联轴器、上下轴承盖和螺母内外圈处共布置13 个温测点。将贴片式PT100 温度传感器安装在热源位置处,HIO-1075 温度采集板采集温度信号并将它传至数控系统,利用华中数控专用数据采集软件SSTT实现在PC(personal computer,个人计算机)端记录温度数据并储存,各传感器安装位置如表1所示,13个温测点的分布如图2所示。如图2(b)所示,用RenishawXL-80 激光干涉仪S采集机床Z向进给系统的热变形数据,激光干涉仪入射镜与折射镜安装在工作台上,反射镜安装在主轴上,激光发射器安装于机床正前方,PC与发射器相连接。激光干涉仪只能间歇测量,试验机床Z向进给系统的效行程为600 mm,每隔50 m 设定一个测点,共13个测点;采用正反双向测量,消除丝杠反向间隙的影响,激光干涉仪测点分布如图3所示。

表1 传感器安装位置Table 1 Installation position of sensors

图2 Z向进给系统温测点分布Fig.2 Layout of temperature measurement points for Z-direction feed system
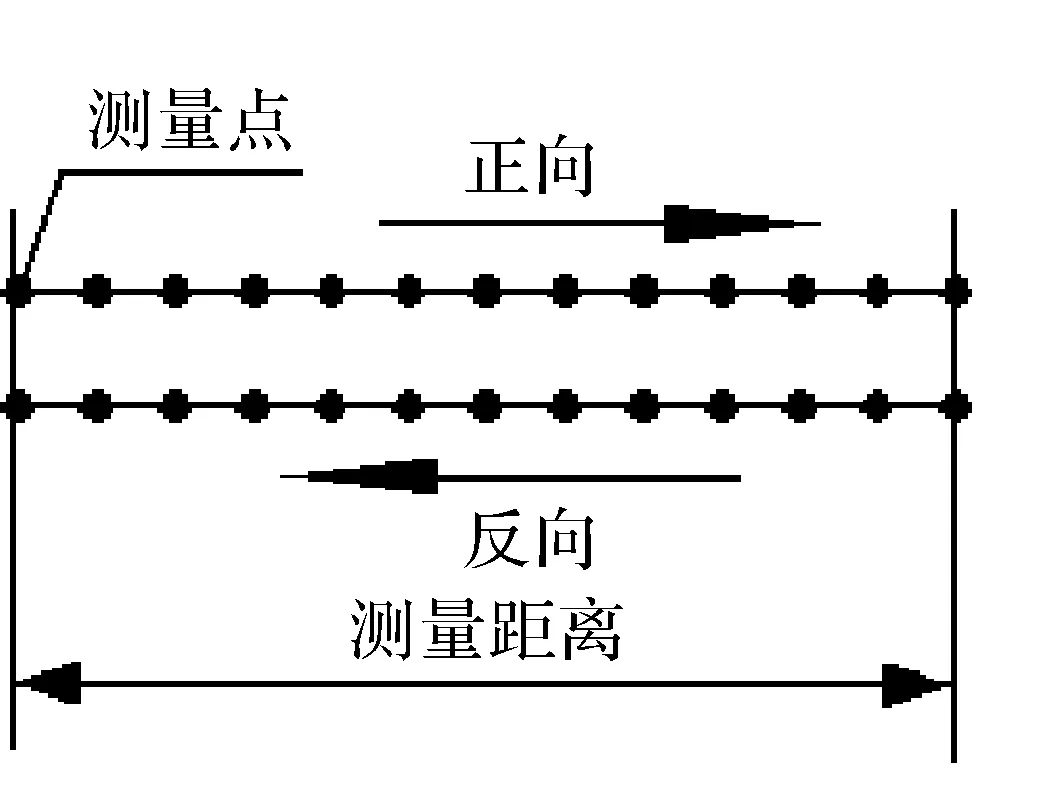
图3 激光干涉仪测点分布Fig.3 Layout of measurement points of laser interferometer
本文拟研究机床从冷机到热平衡阶段的热误差变化规律,采集进给速度为8 000,12 000 和16 000 mm/min时机床热机阶段的温度与热误差数据,共采集48 组热误差数据。以进给速度v=8 000 mm/min为例,机床开机后,主轴保持静止,Z向进给轴以8 000 mm/min的进给速度往复运动,激光干涉仪采样周期为15 min,整个试验时长为240 min。滤波平稳处理后,13 个温测点处温度随时间的变化曲线如图4 所示,由图可知,t=0—150 min 阶段温度上升迅速,在t=150 min 左右基本达到热平衡,t=150—180 min 阶段温度略微上升,t=180 min 后温度基本不再变化。t=0,15,30,45,60,75,90,105,120,135,150 min时热误差曲线如图5所示。
由于各传感器初始温度并不是环境温度,在安装激光干涉仪时,需要上下移动主轴使激光干涉仪的反射光与折射光重合,不可避免地会造成机床部件升温。为保证热误差预测模型的精度,采用温度变化量作为温度变量样本,即ΔTi(t)=Ti(t)-T0。图5中的

图4 温测点温度随时间的变化曲线(v=8 000 mm/min)Fig.4 Variation curve of temperature of temperature measurement points over time(v=8 000 mm/min)

图5 温升阶段Z向进给系统热误差曲线(v=8 000 mm/min)Fig.5 Thermal error curve of Z-direction feed system in temperature rising stage(v=8 000 mm/min)
热误差值以丝杠收缩方向为正,伸长方向为负,因试验时间为冬季,初始测量时丝杠处于收缩状态。
2.3 温测点优化结果
根据1.2 节中互信息值计算原理,以t=0—150 min 阶段机床进给系统各温测点温度变化量ΔTi(t)和热误差变化量Y(t)作为样本。但由于进给系统热误差值与进给轴位置有关,为更准确获取温度变化量与热变形间的相关性,考虑到图5中的热误差与进给位置几乎呈线性关系,采用热误差曲线一次拟合斜率Kj(t)(j=1,2,…,13)代替Y(t)进行互信息值计算。将ΔT、Kj(t)代入式(1),计算得到各温测点的互信息值,如表2所示。
由上文可知,在进给轴上轴承、螺母和下轴承等重要位置均布置了多个温测点,它们均能反映相应位置的发热情况,因此,为消除温测点间的耦合性,结合互信息值计算结果,选择各位置处相关性较高的2个温测点作为主要影响因素,如进给轴上轴处温测点4,5,螺母处温测点7,9,下轴承处温测点10,12,最后得到1,2,4,5,7,9,10,12,13等9个温测点作为主要影响因素。

表2 各温测点的互信息值Table 2 Mutual information value of temperature measurement points
根据改进有序聚类分类法,对上述9个温测点在t=0—150 min 阶段的温度样本ΔTi(t)升序排列并进行规格化处理,计算直径矩阵D和最小误差函数ψ[q(k,l)]。得到的有序聚类结果如表3所示,误差函数值与聚类数的关系曲线如图6所示。

表3 温测点有序聚类结果Table 3 Sequential clustering results of temperature measurement points
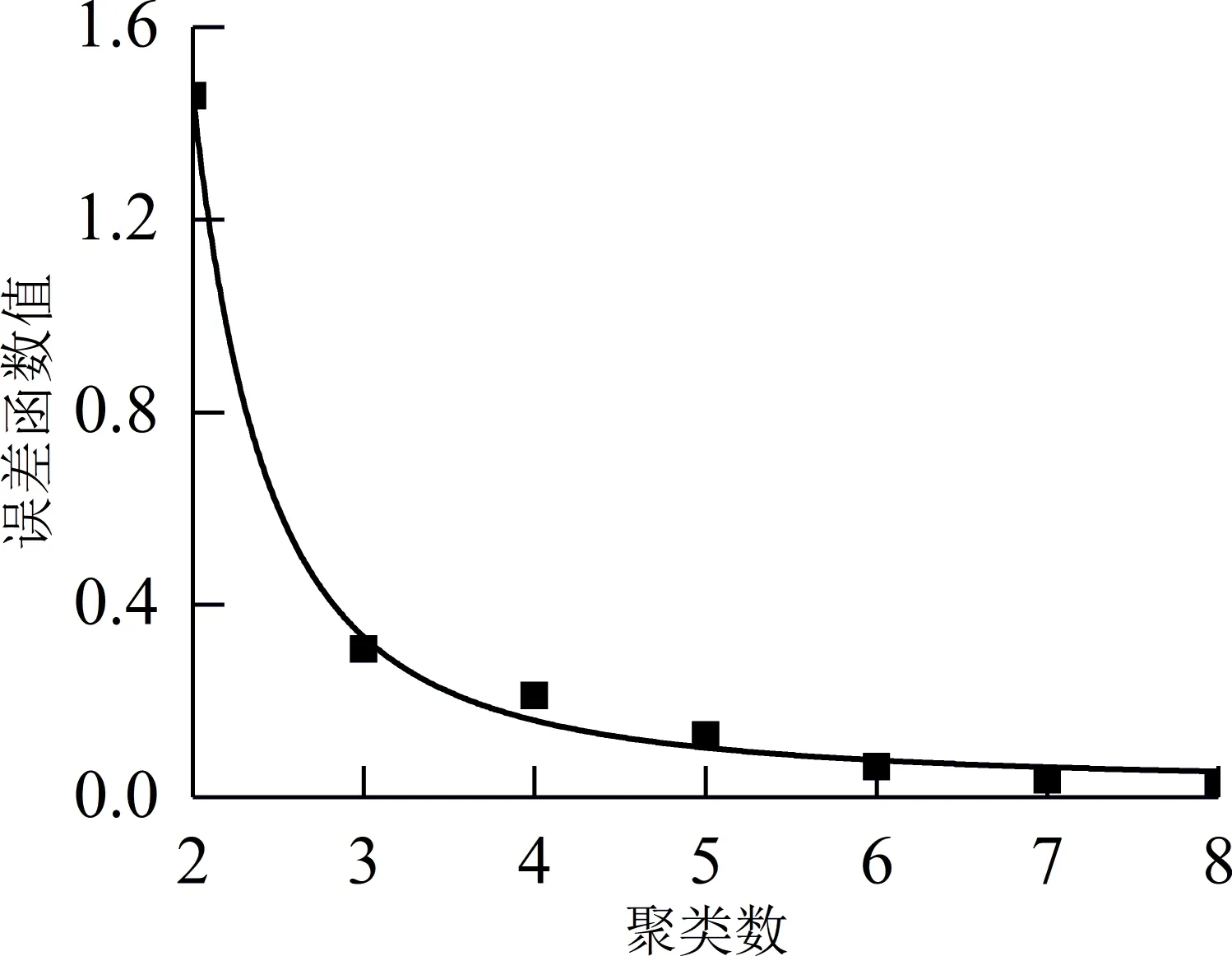
图6 温测点误差函数值与聚类数的关系曲线Fig.6 Relation curve of error function value and number of clusters of temperature measurement points
由图6可以看出,误差曲线在聚类数为3,4,5时均有明显转折,对应建立包含3个测点、4个测点和5个测点的线性回归模型,多个测点属于同一聚类时,选择互信息值大的测点(如分为3类时,测点2,4,5,7,9,10,12属于一类,选取互信息值最大的测点4,此时包含3个测点的热误差多元线性回归模型的输入样本为测点1,4,13的温度变化值)建立热误差模型。由图5 的热误差曲线可以看出,热误差与温度(时间)、进给轴位置有关,温度一定时热误差与进给轴位置近似呈线性变化,因此用E=tanβ(Px-P0)来表示热误差与进给轴位置的关系[19],其中:Px为机床进给轴实时位置,P0为机床进给轴相对零点,tanβ为热误差拟合直线斜率。基于多元线性回归建立立式加工中心Z向进给系统温度变化量与热误差曲线一次拟合直线斜率的回归模型,并对该模型进行统计学分析,结果如表4所示。
分析表4可得如下结论:
1)对不同测点的热误差模型进行F检验时,各模型的F值均在相应的拒绝域且概率p(即显著度Sig.)都小于显著性水平0.05,表明该显著水平下各温测点的温度变化量对热误差的线性影响显著。
2)判定系数R2、标准残差和最大残差直观反映了热误差模型的拟合效果与预测精度,R2越大,表明拟合拟合效果越好,标准残差和最大残差越小,表明精度越高。从表中可以看出对于包含3个测点和4个测点的热误差模型,随着测点的增多,R2增大,标准残差与最大残差减小,但对于包含4个测点和5个测点的热误差模型,即使测点增多,但R2、标准残差和最大残差均不变,说明测点增多虽然会提高热误差模型的精度,但精度的提高却越来越不明显。
3)对各模型的偏相关系数进行t检验时,包含5个测点的热误差模型的ΔT12没有通过t检验,且从相关系数可以看出,ΔT12的贡献率很小。
综上,综合考虑模型精度与鲁棒性要求,选取4个测点1,4,9,13作为最佳温测点。
3 温测点优化结果验证
根据改进有序聚类法得到的最佳温测点,基于多元线性回归建模方法得到机床Z向进给系统的热误差预测模型为:

其中P0由文献[19]中的均值法计算得到,P0=17.98。
采用传统有序聚类法选取误差函数曲线非负斜率α(k)最大时的k值为较优聚类数[15],即有α(3)>α(4)>α(5),建立包含3个测点的热误差预测模型为:

采用灰色关联度模糊聚类法[10]进行温测点优化,并建立包含4个测点的热误差预测模型为:

表4 温测点的热误差模型统计学分析结果Table 4 Statistical analysis results of thermal error model of temperature measurement points

利用上述3种热误差预测模型分别对进给速度v=8 000 mm/min的温升阶段中t=60 min与进给速度v=12 000 mm/min的热平衡阶段中t=150 min时的热误差进行预测,基于3种模型的热误差预测曲线与残差曲线对比分别如图7和图8所示。激光干涉仪的反向位置(600 mm)处因仪器误差影响测量结果,因此观测0~550 mm 位置处各热误差模型的预测结果。从图7和图8发现,相较于利用传统有序聚类法和灰色关联度模糊聚类法得到的热误差预测曲线,利用改进有序聚类法得到的热误差预测曲线在升温和热平衡阶段都与实际测量曲线更加接近,残差变化幅度较小。
为进一步验证3种热误差模型的预测效果,分析了温升阶段与热平衡阶段各模型的均方根误差、最大残差和平均残差,结果如表5和表6所示。表中均方根误差用来描述误差的总体离散程度,残差表示回归模型的拟合值与实测值之间的误差[13]。

图7 温升阶段Z 向进给系统热误差模型预测结果(v=8 000 mm/min,t=60 min)Fig.7 Prediction results of thermal error model of Z-direction feed system in temperature rising stage (v=8 000 mm/min,t=60 min)

图8 Z 向进给系统热平衡阶段热误差模型预测结果(v=12000 mm/min,t=150 min)Fig.8 Prediction results of thermal error model in temperature stage(v=12 000 mm/min,t=150 min)
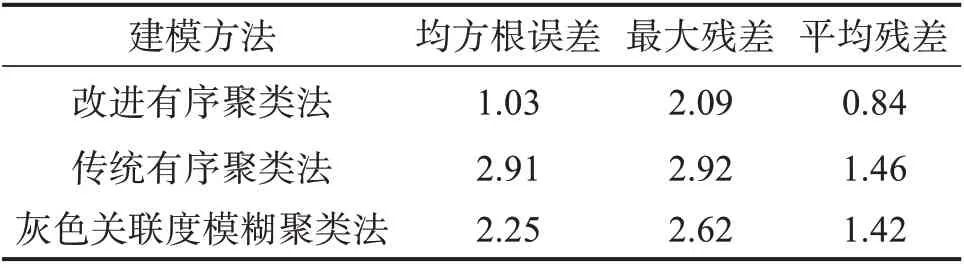
表5 温升阶段Z 向进给系统热误差模型预测效果(v=8 000 mm/min,t=60 min)Table 5 Prediction effect of thermal error model of Zdirection feed system in temperature rising stage (v=8 000 mm/min, t=60 min) 单位:μm
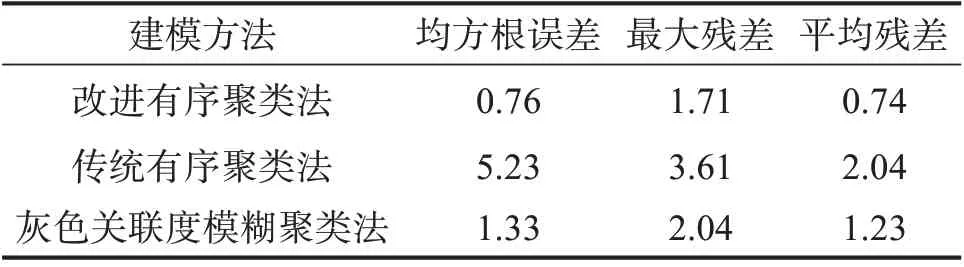
表6 热平衡阶段Z向进给系统热误差模型预测效果(v=12 000 mm/min, t=150 min)Table 6 Prediction effect of thermal error model in temperature balance stage (v=12 000 mm/min,t=150 min) 单位:μm
从表5和表6可以看出,采用改进有序聚类法所建的热误差预测模型在温升阶段和平衡阶段的均方根误差低于1.05 μm,最大残差仅为2.09和1.71 μm,平均残差最小,低于1 μm,且热平衡阶段热误差模型预测精度高于温升阶段。基于改进有序聚类法的热误差模型在热平衡阶段的精度相较于另外2种模型分别提高了65.7%和39.8%。
4 结 论
1)根据立式加工中心进给系统的发热特点,由互信息值初步筛选各发热部件不同位置的同类温测点,并基于改进有序聚类法选取最佳温测点,有效解决了多温测点间共线性的问题,减少了温测点数量,提高了拟合精度和鲁棒性。
2)结合统计学分析与有序聚类法,从显著性检验(F检验和t检验)、拟合效果和残差分析等方面确定最佳聚类数与最佳温测点。相较于传统有序聚类法,该方法直观且全面地分析了温测点数目与回归模型精度的关系,选取了更精确的最佳聚类数。
3)建模实例表明:基于改进有序聚类法建立的热误差模型的均方根误差、最大残差、平均残差分别小于1.05,2.1,1 μm;相较于采用传统有序聚类法和灰色关联度模糊聚类法建立的热误差预测模型,该热误差模型在热平衡阶段的精度分别提高了65.7%和39.8%。

