数控机床整机动态特性评价方法

姜晓飞，张冠伟，胡永秀，张大卫

（天津大学机构理论与装备设计教育部重点实验室，天津300354）

数控机床整机动态性能是指机床整体结构在动态力作用下的响应特性。在机床加工过程中，动态切削力会使刀具和工件产生相对振动，当振幅超过允许范围时，将导致工件表面恶化，刀具磨损加剧，机床加工精度和生产效率降低，严重时机床可能无法正常工作。因此，准确评价数控机床动态特性的优劣非常关键。

针对上述问题，国内外科研人员展开了相关研究，例如：Weck等［1］提出了动态柔度特性分析方法和加工试验方法来鉴定数控机床的动态特性；张广鹏等［2-3］基于模糊数学的原理提出了一种机床整机动态特性评价方法，该方法可同时考虑多项动态性能评价指标，此外他们还应用子结构合成思想建立了机床整机系统的动力学方程，并开发了相应的整机动态性能预测解析软件；刘世豪等［4］建立了数控机床综合性能评价指标体系，用模糊评价法对数控机床各项性能指标进行评价，并采用层次分析法中的1～9 标度法确定各项性能指标的权重系数；Yigit等［5］提出将频率范围内的整机柔度平均值作为评价机床动态性能的指标之一；丁文政等［6］结合时域指标和频域指标，提出了高档数控机床动态性能评价体系，采用模糊综合法建立了机床动态性能评价模型；Altintas 等［7］指出在机床动态特性研究中应重点关注刀尖点频响和整机模态；张生余等［8］通过激振实验，提出通过幅相频率特性来评价机床的动态稳定性，按机床切削稳定边界图来选择加工条件，以提升机床的切削稳定性；张耀满等［9］认为机床主轴系统的动力学特性对机床加工性能的影响很大，应将主轴单元的各阶固有频率作为一项评价指标；Lee等［10］提出了一种在实际系统建立前根据微型机床结构特点来评价其静态和动态特性的方法，通过选择合适的主轴转速来减小机床振动。上述文献针对机床动态特性开展了广泛研究，但未考虑到不同切削参数下，各频率成分对应的切削力幅值不同，引起的机床响应也不相同。此外，正弦扫频信号与实际切削力相差甚远，不能反映切削过程的实际情况。

鉴于数控机床强迫振动的响应与激振力频率成分有关，基于实际切削过程中的动态切削力建立了动态激振力模型。在检验机床动态特性时，通过分频段激励来分析不同频段下刀具和工件末端的相对振动。考虑到工件材料和切削参数不同时，各频率成分对应的刀具切削力幅值会有所差别，机床的动态响应也会不同，拟研究不同工件材料和切削参数下刀具的动态切削力和不同机床的动态特性，并以此判断机床在各个频段的动态特性，比较在相同动态力作用下不同机床的动态特性，以期为机床设计提供参考，为机床出厂前的动态特性评价提供指导。

1 切削力分析及动态激振力模型建立

1.1 切削力理论模型

根据Wang的研究［11］，螺旋立铣刀微元刀刃对工件的切削力为：

式中：tx为每齿进给量，dh为微元刀刃厚度，θ为刀具初始切削角度，kts、krs、kas分别为剪切力切向、径向、轴向切削系数，ktp、krp、kap分别为犁切力切向、径向、轴向切削系数，这些系数与刀具的材料特性相关，由试验确定。

对式（1）积分，得到单齿总切削力为：

式中：p1和p2分别为单位剪切力和单位犁切力，q1和q2分别为剪切力与犁切力切削系数矩阵，φ为刀具旋转角，α为刀具螺旋角，β为切削点到起切点的周向包角，da为切削深度，z为窗函数，R为刀具半径。

假设立铣刀有N个齿，则其总切削力为：

式中：F为多齿总切削力，fk为第k个齿的切削力，βp为齿间角。

1.2 切削试验及参数识别

上述切削力模型中的参数需通过切削试验来识别。切削试验中，试件材料为6061铝合金和45号钢。切削参数如下：切削深度为1，2，3 mm；每齿进给量为0.05，0.10，0.15 mm；转速为500，750，1 000 r/min；切削宽度为0.5R，1.0R，1.5R，2R。4种切削宽度下的切削几何模型如图1所示，图中wc表示切削宽度。

切削试验中，选用的刀具为株洲钻石切削刀具股份有限公司生产的通用硬质合金立铣刀GM-4ED20.0，其直径为20 mm，螺旋角为45°；选用的数控机床为立式铣床哈挺VMC600Ⅱ；切削力信号通过Kistler公司生产的9257b测力平台以及配套的电荷放大器、数据采集系统（含DynoWare 数据分析软件）采集，其中压电传感器在X、Y、Z三个方向的灵敏度分别为-7.826，-7.823，-3.769 pC/N，量程为-5 ～5 kN。切削试验平台如图2所示，基于选取的切削参数进行切削试验并采集切削力。

图1 4种切削宽度下的切削几何模型Fig.1 Cutting geometry models with four cutting widths

图2 切削试验平台Fig.2 Cutting test platform

根据平均切削力系数模型［12］和切削力试验数据，用最小二乘法识别并确定立铣刀切削力系数kts、krs、kas、ktp、krp、kap，结果如表1所示。

表1 立铣刀切削力系数Table 1 Cutting force coefficients of vertical milling单位：N/mm2

基于切削力理论模型计算不同切削参数下的动态切削力，并与切削力试验值进行对比，如图3所示，结果显示两者吻合度较高。

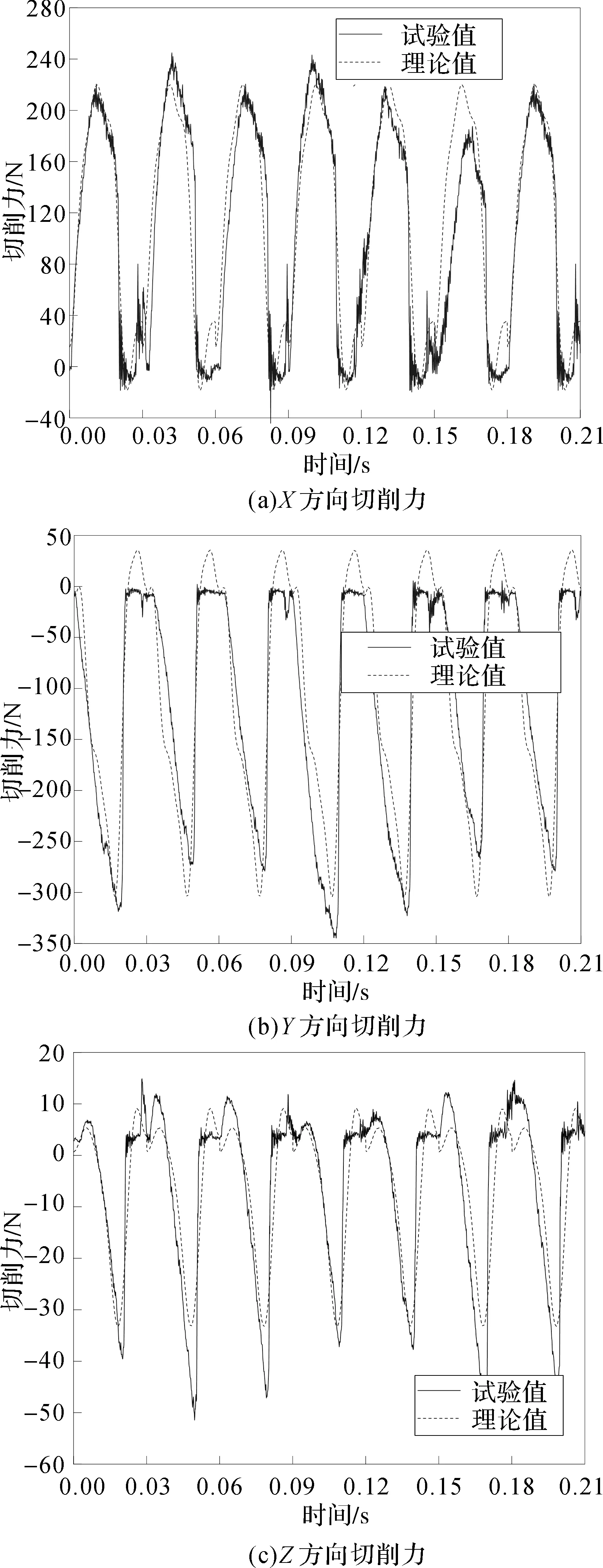
图3 动态切削力理论值与试验值对比Fig.3 Comparison between theoretical values and experimental values of cutting force

图3显示动态切削力呈周期性变化，因周期函数可以用傅里叶级数展开，故将动态切削力展开成余弦级数形式并分析不同切削参数下切削力的主要频率成分。切削力的余弦级数形式可表示为：

式中：an为第n个频率的系数，a0为常数项系数，a为刀具角速度。

1.3 切削力频率成分分析

当转速相同时，不同切削条件下切削力有相同的频率成分，但同一频率对应的切削力幅值不同。为了确定各频率成分对应的切削力幅值与切削参数的关系，比较不同切削宽度、每齿进给量下各频率成分对应的切削力幅值。当切削深度为3 mm，转速为500 r/min，试件材料为6061铝合金时，4种切削宽度下X、Y、Z方向切削力的频率成分及对应的幅值分别如图4至图6所示。

图4 X方向切削力的频率成分及对应的幅值Fig.4 Frequency component and corresponding amplitude of cutting force in X direction

图5 Y方向切削力的频率成分及对应的幅值Fig.5 Frequency component and corresponding amplitude of cutting force in Y direction

图6 Z方向切削力的频率成分及对应的幅值Fig.6 Frequency component and corresponding amplitude of cutting force in Z direction

由不同切削条件下各频率成分对应的X、Y、Z方向切削力幅值可知，不同切削宽度下相同频率成分对应的切削力幅值相差较大；在相同切削宽度下，各频率成分对应的切削力幅值与每齿进给量呈线性关系。

1.4 动态激振力模型建立

根据上文的分析，可以将切削深度为3 mm，转速为500 r/min，试件材料为6061铝合金，相同切削宽度下的动态切削力表示成关于每齿进给量的函数。其余2个切削深度下各频率成分对应的切削力幅值特征与上述情况一致，也可表示成关于每齿进给量的函数。

当转速不同或试件材料不同时，动态切削力的频率成分不同。在上述切削力频率成分分析的基础上，分析不同转速和不同试件材料下动态切削力的频率成分。当转速为750或1 000 r/min时，各频率成分对应的切削力幅值特征与上述情况一致，也可表示成关于每齿进给量的函数。同样，在试件材料为45号钢时，动态切削力也可表示成关于每齿进给量的函数。

基于上述不同切削参数下动态切削力各频率成分的特点，建立动态激振力模型，该激振力模型以每齿进给量为自变量，能够表征不同试件材料、转速、切削宽度、切削深度和每齿进给量下的动态切削力，如公式（5）所示。由于高频率和切削力幅值较小时对应的频率对机床的影响较小，可将这部分频率成分删去。根据切削力是否包含该频率成分，取系数wn=1或0。将动态切削力作为激振力，研究机床在不同频段切削力下的动态特性。

式中：knt+bn为不同每齿进给量下动态切削力各频率成分的系数，代表不同每齿进给量下该频率成分包含的能量，k0t+b0为不同每齿进给量下动态切削力中的静态部分。

2 数控机床动态特性仿真分析

2.1 数控机床有限元模型建立

为分析数控机床在不同频段下的动态特性以及比较不同机床动态特性的优劣，用ANSYS有限元分析软件建立2台机床的有限元模型并进行相应仿真分析。鉴于机床结合面的刚度和阻尼对整机动力学响应的影响较大，除了定义机床各个部件材料属性之外，在各结合面上设置弹簧-阻尼单元［13-15］以模拟真实的接触状况，其刚度和阻尼根据Guo，Deng等［16-17］提出的方法确定。将丝杠和螺母简化为圆柱和圆筒，滚动结合部用1组弹簧-阻尼单元等效，在圆周方向上，弹簧-阻尼单元均匀分布，数量一般为4～8个；在丝杠-螺母副轴向方向上，将螺旋滚道简化为垂直于丝杠轴线的若干个环形滚道，间距为丝杠的导程［18］。滚柱在导轨和滑块间滚动，形成滚动结合面；导轨与机床结构件之间通过螺栓连接；滑块与工作台通过螺栓连接，形成螺栓连接结合面，在各个结合面间设置弹簧-阻尼单元。滚动体在内、外圈间滚动，形成滚动结合面。在数控机床有限元模型中，将整根轴承简化为1组弹簧-阻尼单元。对于螺栓连接结合面，以床身和立柱之间的固定结合面为例，将螺栓简化为弹簧-阻尼单元。2 台数控机床的有限元模型如图7所示。

2.2 数控机床末端振动瞬态分析

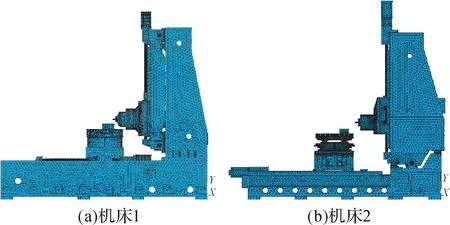
图7 数控机床有限元模型Fig.7 Finite element model of NC machine tool

由上述分析可知当切削参数变化时，各频率成分对应的切削力幅值也会发生变化，因此通过分频段激励来研究切削参数对数控机床动态特性的影响。基于转速为500 r/min、切削宽度为0.5R、切削深度为3 mm时的动态激振力模型，将切削力频率成分划分为低频（0～50.1 Hz）、中频（50.2～100.2 Hz）和高频（100.3～150.3 Hz）三个频段，在刀具和工件上分别施加大小相等、方向相反的动态激振力以进行仿真分析，通过提取刀具和工件间的相对位移，分别计算不同频段下机床末端X、Y、Z方向的动刚度，并比较不同机床在受到相同激振力时的动态特性。

图8 所示为不同频段下机床末端X方向动刚度与每齿进给量的关系曲线。其中，图8（a）为切削6061铝合金时机床1末端的X方向动刚度，图8（b）为切削6061铝合金时机床2末端的X方向动刚度，图8（c）为切削45号钢时机床1末端的X方向动刚度，图8（d）为在切削45号钢时机床2末端的X方向动刚度。

图8 机床末端X方向动刚度与每齿进给量的关系曲线Fig.8 Relation curve of X-direction dynamic stiffness at the end of machine tool and feed per tooth

从图8可以看出：2台机床在低频段下X方向动刚度较小，说明机床在低频段下X方向动态特性较差；在切削同一材料试件时，机床2 在低频段下X方向动刚度略大于机床1（中、高频段下机床末端的振动位移很小，可忽略），表明在低频段下机床2的X方向动态特性更好；切削6061铝合金时机床在低频段下X方向动刚度要大于切削45号钢时，表明2台机床在切削铝合金时X方向动态特性较优。

图9 所示为不同频段下机床末端Y方向动刚度与每齿进给量的关系曲线。其中，图9（a）为切削6061铝合金时机床1末端的Y方向动刚度，图9（b）为切削6061铝合金时机床2末端的Y方向动刚度，图9（c）为切削45号钢时机床1末端的Y方向动刚度，图9（d）为切削45号钢时机床2末端的Y方向动刚度。

图9 机床末端Y方向动刚度与每齿进给量的关系曲线Fig.9 Relation curve of Y-direction dynamic stiffness at the end of machine tool and feed per tooth

从图9可以看出：在切削铝合金时，2台机床在低频段下Y方向动刚度较小，说明此时机床在低频段下Y方向动态特性较差；在切削45 号钢时，2 台机床在低、中频段下Y方向动刚度较小，说明此时机床在低、中频段下Y方向动态特性较差；在切削同一材料试件时，机床2的Y方向动刚度小于机床1，说明机床1在Y方向的动态特性更优；切削6061铝合金时机床的Y方向动刚度大于切削45号钢时，表明2台机床在切削铝合金时Y方向动态特性较优。

图10所示为不同频段下机床末端Z方向动刚度与每齿进给量的关系曲线。其中，图10（a）为切削6061铝合金时机床1末端的Z方向动刚度，图10（b）为切削6061铝合金时机床2末端的Z方向动刚度，图10（c）为切削45号钢时机床1末端的Z方向动刚度，图10（d）为切削45 号钢时机床2 末端的Z方向动刚度。

从图10可以看出：在切削不同材料试件时，机床在低频段和中频段下Z方向动刚度较小，说明机床在低、中频段下Z方向动态特性较差；在切削相同材料试件时，机床2的Z方向动刚度小于机床1，说明机床1的Z方向动态特性较优；在切削6061铝合金和45号钢时机床的Z方向动刚度差别不大，表明切削不同材料试件时机床Z方向动态特性相差不大。

3 激振试验验证

3.1 激振试验

为验证上述有限元分析结果的准确性，对2台机床进行激振试验，激振试验台如图11所示，通过采集机床末端的相对振动位移来计算其相对动刚度。选用宝应县宝飞振动仪器厂生产的DJ-20非接触式激振器进行激振，其最大激振力为20 N，工作频率范围为1～500 Hz，激振力波形失真度小于5%；用电容传感器采集机床末端的相对振动位移；在刀杆靠近主轴端处贴应变片以采集刀杆受到的激振力。基于采集的试验数据计算机床在各个频段下X、Y、Z方向动刚度，并与有限元分析结果进行比较，结果如表2至表5所示。

图10 机床末端Z方向动刚度与每齿进给量的关系曲线Fig.10 Relation curve of Z-direction dynamic stiffness at the end of machine tool and feed per tooth

图11 激振试验台Fig.11 Excitation test bench

表2 机床1切削6061铝合金时的动刚度Table 2 Dynamic stiffness of machine tool 1 during cutting 6061 aluminum alloy

表3 机床2切削6061铝合金时的动刚度Table 3 Dynamic stiffness of machine tool 2 during cutting 6061 aluminum alloy

表4 机床1切削45号钢时的动刚度Table 4 Dynamic stiffness of machine tool 1 during cutting 45# steel

表5 机床2切削45号钢时的动刚度Table 5 Dynamic stiffness of machine tool 2 during cutting 45# steel

由表中数据可知，激振试验结果与有限元分析结果的相对误差不大，验证了机床动态特性有限元分析结果的准确性。

3.2 激振试验结果与扫频分析结果比较

正弦扫频分析用于研究单个频率激励下机床的动态特性，当激振频率等于固有频率时，机床的振动较大。然而机床在实际切削时会同时受到多个频率的激励，且各个频率对应的切削力幅值不同，此时机床为非线性系统，不能将各个频率激励下的振动位移简单叠加。由上文可知不同切削参数和试件材料下，切削力的主要频率成分以及各频率成分对应的切削力幅值不同，机床在复杂多变切削力作用下的动态特性不能用正弦扫频这样单一的信号来分析。

正弦扫频信号作用下机床1末端的振动频谱如图12 所示，图中峰值对应的固有频率分别为30.5，44.5，62.1 Hz。分频段切削力作用下机床1末端的振动频谱如图13所示。

对比正弦扫频响应结果与切削力激振作用下的振动频谱可知，后者更能准确地反映机床振动的频域信息。结合机床各个方向的模态，可找到振动最大的部位，这可为机床动态特性优化提供参考。

4 结 论

图12 正弦扫频信号作用下机床1末端的振动频谱Fig.12 Frequency spectrum of vibration at the end of machine tool 1 under the action of harmonic sweep signal

1）提出了一种数控机床动态特性评价方法，该方法能够准确判断数控机床在不同切削力作用下的动态特性。

2）切削参数和试件材料会影响切削力的频率成分及对应的幅值；通过分频段激励，可以检验机床在各频段切削力作用下的动态特性。

3）通过搭建激振试验平台，用真实的切削力对机床进行激振，验证了有限元分析结果的准确性。

4）通过分析机床末端相对振动的频域信号，结合机床各个方向上的模态，可以找出机床在切削力作用下的主要振动部位，这可为机床动态特性优化提供参考。

图13 分频段切削力作用下机床1末端的振动频谱Fig.13 Frequency spectrum of vibration at the end of machine tool 1 under the action of variable sub-band cutting force