高精度超高压液相泵等面积平滑补偿控制方法
谭 旭,王晓阳,殷 参,曾 婷,魏兴亚
(北京卫星制造厂有限公司,北京100094)
液相泵是将有机相液体与水相液体分别按预定 流量输出并进行混合的装置,主要应用于液相色谱分析领域,将水、乙睛、甲醇、乙醇、丙酮等任意2种液体(含有机相和水相)按规定流量混合后注入色谱分析柱,使样品形成其所含物质的色谱[1]。2种输出液体的流量精度会直接影响色谱分析柱中样品的色谱波形,流量精度低会导致形成的色谱不准确或不能形成色谱,从而无法进行准确的色谱分析[2]。
传统的液相泵控制方法是通过构建泵体的运动方程,使泵体直接按运动方程运行,但该方法的缺陷是在加速度拐点处,尤其是在初始速度较高的加速度拐点处,由于自身惯性,液相泵电机会抖动,致使液相泵瞬时转速失稳,影响输出液体的流量精度[3-5]。
针对液相泵在加速度拐点处出现电机抖动的问题,根据泵体的运动方程,提出一种等面积平滑补偿控制方法,以期使液相泵在初始速度较高的加速度拐点处平稳过渡;同时,由于进行了平滑处理,液相泵在单个运行周期内的总位移会减小,而位移减小会使液相泵流量变小,从而影响最终的输出液体流量精度[6],因此需对减小的位移进行补偿,以确保在液相泵单个运行周期结束前补齐位移,使液相泵的位移总量不变,提高其输出液体的流量精度。
1 S型曲线优化方法
随着自动控制技术的不断发展,为了减少电机在加速度拐点处的抖动,确保电机运行过程中的精度,在实际工程应用中,会对电机运动方程进行优化。目前多采用S型曲线优化方法,该方法因被控对象加减速阶段的速度曲线呈S形而得名,它包含7段三次样条函数[7-9],即将速度曲线按加速度类型分成7个阶段:加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段,如图1所示。
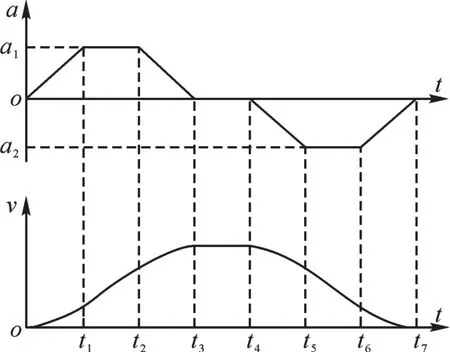
图1 S型曲线Fig.1 S-type curve
由图1可见,理论上可以通过对加速度的控制,使速度平滑过渡,不产生“拐点”,但这就要求液相泵在实际运行过程中需在速度为零时迅速换向,保证吸液与排液过程快速切换,否则,由于液体在微小体积下的“粘连效应”,有可能出现“断流”现象,从而影响液相泵精度。在总位移不变的前提下,若要确保速度为零处的快速换向而使电机保持匀加速运动,势必会影响原运行曲线的形状,导致泵体运动相位改变,从而影响液相泵的精度,由此说明液相泵电机控制不能直接采用传统的S型曲线进行优化。
对此,笔者提出了一种等面积平滑补偿控制方法,在不改变液相泵运动相位的前提下,只对电机在高速运行状态下的加速度拐点进行优化,而不对电机在低速状态下的速度曲线进行优化,这样既保证了液相泵的运动相位不变又减少了电机抖动,更有利于液相泵的实际应用。
2 液相泵控制系统组成
液相泵的核心为传动控制系统,主要由上位机、主控制器、驱动电路、电机、编码器和泵体组成,如图2所示。液相泵共包含2个泵体和4个缸体:1号泵体由1号泵主缸与1号泵副缸组成,用于完成一种液体(有机相)的吸入与排出;2 号泵体由2 号泵主缸与2号泵副缸组成,用于完成另一种液体(水相)的吸入与排出;2个泵体中的4个缸体分别按照主控制器输出的运动方程完成动作,实现2种液体的混合。

图2 液相泵控制系统硬件组成框图Fig.2 Block diagram of hardware composition of liquid pump control system
在液相泵实际运行过程中,上位机将流量、介质种类等参数传输给主控制器,主控制器的曲线生成模块根据上位机输入的参数编译4个缸体的运动方程并传输给平滑补偿模块,平滑补偿模块对每个缸体在高初始速度下的加速度拐点进行平滑补偿,完成平滑补偿后平滑补偿模块将新的运动方程传输给驱动电路,运动方程经驱动电路解码后再传输给电机以驱动液相泵的每个缸体运动,编码器实时采集电机实际运行数据并反馈给主控制器的PID(proportion integration differentiation,比例积分微分)模块进行修正,修正后的运行数据再传输给曲线生成模块以对运动方程进行完善,形成闭环[10-11]。
3 等面积平滑补偿控制原理
等面积平滑补偿控制方法是一种解析计算方法,用于平滑补偿模块对曲线生成模块所输出的4个缸体的运动方程在高初始速度下的加速度拐点进行平滑处理并在单个运行周期结束前补齐因平滑处理而减小的位移,以提高液压泵最终的流量精度。
以液相泵的1号泵主缸为例,对1号泵主缸的运动方程进行解析,提取拐点信息:

式中:S1、S2分别为吸入、排出液体时的位移;v1、v2分别为吸入、排出液体时达到的最高平稳速度;ti(i=1,2,…,7)分别为第i个加速度拐点对应的运行时间。
根据式(1)和式(2)构建1号泵主缸的运行曲线,如图3所示。

图3 1号泵主缸运行曲线Fig.3 Running curve of master cylinder of pump 1
在1号泵主缸吸入液体时,加速度拐点1处的初始速度为0 mm/s,加速度拐点2,3 处的初始速度较高,加速度拐点4处的初始速度较低,由此可知,拐点1 与拐点4 不会对电机运行造成影响,只有拐点2 与拐点3会造成电机抖动,故只需对拐点2与拐点3进行平滑处理。为确保吸入液体总量不变,必须保证吸入液体时1号泵主缸的位移不变,故需在t4前将因对拐点2,3进行平滑处理而减小的位移补齐。
在1号泵主缸排出液体时,加速度拐点5,6处的初始速度较高,加速度拐点7处的初始速度较低,由此可知,拐点7不会对电机运行造成影响,只有拐点5与拐点6 会造成电机抖动,故只需对拐点5 与拐点6进行平滑处理,为确保排出液体总量不变,必须保证排出液体时1号泵主缸的位移不变,故需在t7前将因对拐点5,6进行平滑处理而减小的位移补齐。
首先对拐点2进行平滑处理,为确保不大幅度改变1号泵主缸运行曲线且保证平滑调整后的平滑度,确定拐点2的平滑处理时间为:

式中:系数e可根据流量进行调节,0.01≤a≤0.08。
在确定了tc2后,确定拐点2附近运行曲线的开始时间ta2以及结束时间tb2:

根据平滑处理后运行曲线的形式,构建拐点2附近速度与时间的三元二次方程:

式中:m、n、k为三元二次方程的系数。
将ta2、t2、tb2及各自对应的速度va2、vs2、vb2代入式(6),可得:
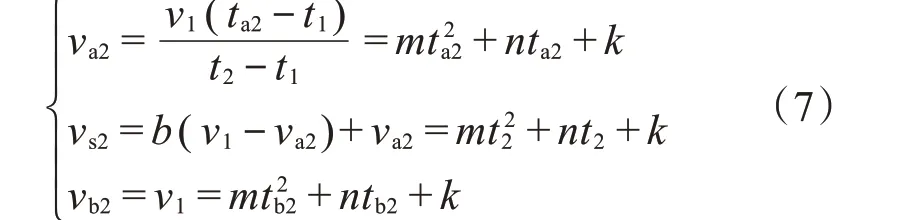
式中:系数b可根据平滑需求进行调节,0.5<b<1。
根据式(7)计算出m、n、k的值,然后对ta2—tb2阶段的速度进行积分,得出经过平滑处理后,该段时间内1号泵主缸的位移为:
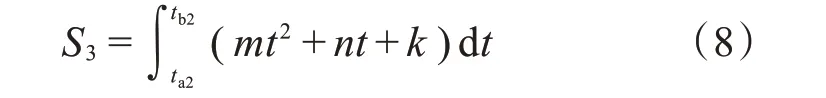
平滑处理前,ta2—tb2阶段1号泵主缸的位移为:

则因平滑处理而减小的位移为:

平滑处理前后拐点2附近的运行曲线如图4所示。

图4 平滑补偿前后拐点2附近运行曲线对比Fig.4 Comparison of running curves near inflexion point 2 before and after smoothing compensation
在完成对拐点2的平滑处理后,对拐点3进行平滑处理,拐点3的平滑处理时间为:

根据式(11)确定拐点3 附近运行曲线的开始时间ta3与结束时间tb3:

根据平滑处理后运行曲线的形式,构建拐点3附近速度与时间的三元二次方程:

式中:r、s、u为三元二次方程的系数。
将ta3、t3、tb3及各自对应的速度va3、vs3、vb3代入式(14),可得:

式中:系数c、d可根据需求进行调节,其中0<c<0.5,0.5<d<1。
根据式(15)计算出r、s、u的值,并计算平滑处理前后2条运行曲线的交点对应的时间tp:

根据确定的参数,对ta3—tp阶段的速度进行积分,得出经过平滑处理后,该段时间内1号泵主缸的位移为:

平滑处理前,ta3—tp阶段1号泵主缸的位移为:

则因平滑处理而减小的位移为:

由于平滑处理,使得1号泵主缸吸液时的总位移减小,导致吸入液体总量减少,严重影响精度,因此必须在吸入液体结束前(即t4前)将位移补齐。
在t=tp时,对1号泵主缸进行位移补偿,补偿曲线初始阶段为曲线段,到tx后变为直线段。对tp—tx内的速度进行积分,得出该段时间内1号泵主缸的位移为:

而tx—t4阶段1号泵主缸的位移为:
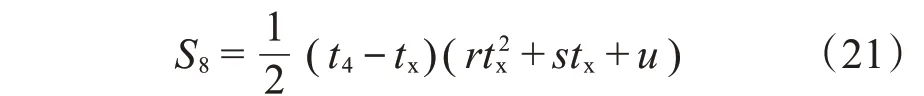
平滑补偿前,tp—t4阶段1号泵主缸的位移为:

则最终可补偿的位移为:

以平滑补偿前后1号泵主缸吸液时的总位移不变为约束条件,得:

联立上述公式计算出tx,至此便完成了对1号泵主缸原运行曲线拐点2,3的平滑补偿处理,并计算出了t1—t4阶段1号泵主缸的速度。图5为平滑补偿处理前后拐点3附近运行曲线的对比。对1号泵主缸运行曲线进行平滑补偿后,在保证泵体位移总量不变的情况下,既防止了电机抖动,又提高了流量精度。

图5 平滑补偿前后拐点3附近运行曲线对比Fig.5 Comparison of running curves near inflexion point 3 before and after smoothing compensation
同理,计算出拐点5 与拐点6 的平滑补偿参数,完成对1号泵主缸在1个运行周期内所有高初始速度的加速度拐点的平滑补偿,平滑补偿前后1号泵主缸运行曲线的对比如图6所示。由图可得,等面积平滑补偿控制方法将原运行曲线中高初始速度的加速度拐点均进行了平滑处理,消除了原运行曲线的高速“尖点”,并进行了位移补偿,确保平滑补偿前后1号泵主缸位移相等。

图6 平滑补偿前后1号泵主缸运行曲线对比Fig.6 Comparison of running curves of pump 1 master cylinder before and after smoothing compensation
4 试验验证
为验证等面积平滑补偿控制方法的可行性,以高精度超高压液相泵为例进行电机运行试验、流量精度检测试验、响应速度检测试验和超高效分离试验。高精度超高压液相泵实物图如图7所示。

图7 高精度超高压液相泵实物图Fig.7 Physical map of high-precision ultra-high pressure liquid pump
4.1 电机运行试验
以液相泵1 号泵主缸运行曲线(工作流量为0.5 mL/min)为输入条件,开展电机运行试验,验证电机运行效果。根据原运行曲线设定初始参数:v1=3.2 mm ⋅s-1、v2=2.5 mm ⋅s-1、t1=15.7 s、t2=16.2 s、t3=20.1 s、t4=20.8 s、t5=21.7 s、t6=27.4 s、t7=27.9 s,在进行平滑补偿前,电机编码器反馈的电机实际运行曲线如图8所示。

图8 平滑补偿前电机实际运行曲线Fig.8 Actual running curve of motor before smoothing compensation
利用等面积平滑补偿控制方法对1号泵主缸运动曲线进行平滑补偿后,电机编码器反馈的电机实际运行曲线如图9所示.

图9 平滑补偿后电机实际运行曲线Fig.9 Actual running curve of motor after smoothing compensation
对比图8和图9可得,采用等面积平滑补偿控制方法对1号泵主缸运行曲线进行平滑补偿后,在高初始速度的加速度拐点处,电机可以平稳地实现变速。通过实际测试可知,在平滑补偿前,电机会有轻微抖动,在平滑补偿后,电机没有出现抖动现象,且平滑补偿前后1号泵主缸的总位移一致。
4.2 流量精度检测试验
在完成单电机运行试验后,进行液相泵整机的输出液体流量精度检测试验。分别对采用平滑补偿控制方法前后液相泵输出液体的流量进行检测,液相泵工作流量为0.5 mL/min,每180 s采集一次数据,各采集5次,按公式(25)至(27)计算相对标准偏差(relative standard deviation,RSD),以此表征液相泵输出液体的流量精度,RSD越小,说明液压泵输出液体的流量精度越高。

式中:Li为单次流量采集值,z为总采集次数,-L为流量平均值,σ-L为标准偏差。
采用平滑补偿控制方法前后液压泵输出液体的流量精度对比如表1所示。

表1 平滑补偿前后液相泵输出液体流量精度对比Table 1 Comparison of flow precisions of output liquid of liquid pump before and after smoothing compensation
由表1可得:液相泵在未采用平滑补偿控制方法前,输出液体的流量精度为0.081%;在采用平滑补偿控制方法后,输出液体的流量精度为0.055%。由此说明等面积平滑补偿控制方法有效提高了液相泵输出液体的流量精度。
4.3 响应速度检测试验
在实际应用中,需要根据实际需求改变液相泵流量,因此还需要验证流量变化过程中液压泵的响应速度,若响应速度较慢,则会影响最终的液体分离效果。本试验中,将丙酮注入液相泵1号泵中,纯水注入2号泵中,采用高分辨率纯化色谱仪对液相泵输出的混合液体进行吸光度分析[12],结果如图10所示。

图10 平滑补偿前后液相泵响应速度对比Fig.10 Comparison of response speeds of liquid pump before and after smoothing compensation
由图10可见:平滑补偿前液相泵对流量变化的响应并不灵敏,在控制信号变化后,电机因变速而产生抖动,则最终的响应速度曲线无法呈现明显的台阶状;而在平滑补偿后,液相泵流量变化的响应非常灵敏,其响应速度曲线呈现清晰的台阶状,说明平滑补偿能够实现液相泵对流量变化的快速响应。
4.4 超高效分离试验
液相泵是色谱分析系统的核心部件,将液相泵接入色谱分析系统,通过超高效分离试验[13]来检验液相泵的实际性能,即检验液相泵在短时间内对样品的分离性能。
将液相泵接入色谱分析系统,1号泵注入乙腈,2号泵注入纯水,对羟基苯甲酸酯样品进行分离。图11为液相泵运行曲线平滑补偿前测试样品的分离峰形,图12为液相泵运行曲线平滑补偿后测试样品的分离峰形,图13 为液相泵运行曲线采用传统S 型曲线优化后测试样品的分离峰形。

图11 平滑补偿前测试样品分离峰形Fig.11 Separated peak shape of testing sample before smoothing compensation

图12 平滑补偿后测试样品的分离峰形Fig.12 Separated peak shape of testing sample after smoothing compensation

图13 采用S型曲线优化时测试样品的分离峰形Fig.13 Separated peak shape of testing sample when using Stype curve optimization
由图11 与图12 可见,样品分离后都呈现4 个清晰的峰形,分别对应羟基苯甲酸甲酯、羟基苯甲酸乙酯、羟基苯甲酸丙酯和羟基苯甲酸丁酯。液相泵运行曲线平滑补偿后,测试样品的峰形更为清晰、线条更直、间隔更大,且没有形成多余的峰,这就使得每个峰的峰面积能计算得更为准确,计算得到的各组分浓度更接近实际浓度,其中:平滑补偿后浓度误差小于0.13%,平滑补偿前浓度误差小于0.57%,由此可见对液相泵运行曲线进行平滑补偿后,液相泵对样品的分离效果更佳,有利于组分检测分析。
由图13 可见,采用传统S 型曲线对液相泵运行曲线进行优化后,由于相对较大地改变了泵体的运动相位,使得液相泵在分离样品过程中无法使样品组分完全分离,导致样品各个峰形出现“粘连”现象,从而无法准确计算出每个峰的峰面积,即无法准确计算出各组分浓度,由此说明传统S型曲线并不适用于液相泵运行曲线优化。
5 结 论
提出的等面积平滑补偿控制方法有效解决了液相泵电机在高初始速度的加速度拐点处抖动的问题,确保电机在高速运动过程中平稳变速,并通过试验验证,得到以下2个结论:
1)流量精度检测试验结果表明,等面积平滑补偿控制方法可以使液相泵输出液体的流量精度从0.081%提高到0.055%。
2)响应速度检测试验与超高效分离试验结果表明,等面积平滑补偿控制方法使液相泵对流量变化的响应更为灵敏,分离样品的效果更佳,可将浓度误差从0.57%提高到0.13%。

