白鹤滩水电工程左岸玄武岩层间错动带渗透破坏预测与防治模拟*
周志芳 沈 琪 石安池 庄 超 陈 朦 李鸣威
(①河海大学地球科学与工程学院, 南京 211100, 中国) (②华东勘测设计研究院, 杭州 311122, 中国)
0 引 言
白鹤滩水电工程位于金沙江下游河段(攀枝花至宜宾),坝区地势北高南低,地质条件复杂。坝区玄武岩各岩层之间发育凝灰岩夹层,在构造应力的作用下形成了缓倾角、贯穿性层间错动带(Chen et al.,2018)。这些错动带的渗透特性是白鹤滩水电站尤为关注的重点问题之一,是构成工程整体和局部稳定安全的重要控制因素。
错动带是一类具有很强非均质性的构造(Faulkner et al.,2003),内部充填物可划分为夹泥、岩屑夹泥、碎粒和岩块4种类型(Zhou et al.,2018),在构造作用下由断层岩石中相对狭窄区域内的剪切作用而形成(Wibberley et al.,2008; 高平等, 2019)。孟祥瑞等(2018)对层间错动带岩体的剪切特性进行了研究,指出含水率对错动带内泥化夹层材料抗剪强度有着显著影响。朱凌等(2018)在此基础上进行动三轴试验研究,试验表明地震可能导致错动带发生液化。国内学者对白鹤滩水电站错动带进行了较多的研究,徐鼎平等(2012)对层间材料和土/岩接触面的剪切力学特性进行了研究,指出了错动带强烈的不均匀性,并通过剪切试验和数值模拟的方法分析了错动带对地下厂房稳定性的影响(Xu et al.,2012, 2013, 2015); 孟国涛等(2016)针对白鹤滩地下洞室群不同部位的典型围岩变形破坏机制进行分析,指出需要设计混凝土置换洞与系统支护相结合的锚固区,从而控制层间带的错动变形; Zhou et al.(2018)建立了层间错动带二维概化模型,进行数值模拟分析错动带分段渗透系数分布规律,并给出了大尺度条件下C2、C3层间错动带渗透系数建议取值; 李韬等(2018)利用离散元软件建立左岸边坡开挖分析模型,分析指出边坡坡内发育的软弱结构面是控制左岸岩质边坡变形的主导因素; 程普等(2018)评价了左岸厂区截渗洞与帷幕灌浆截断渗漏通道的效果,指出虽然渗流控制措施能够较好地截断渗漏通道,但是排水孔揭穿C2位置处渗透比降仍然较大。
以上研究表明,白鹤滩坝区内发育的错动带各向异性十分明显,且透水性好,是主要的渗漏通道,对工程渗流稳定影响较大。白鹤滩水电站水库正常蓄水位为825im,金沙江水位590im,建成蓄水后上下游水头差可达235im。由于大坝上下游存在较大的水头差,断层、错动带等透水性较好的结构面贯穿整个坝区,在防渗帷幕和排水孔等阻水排水结构的共同作用下,整个厂坝区的渗流场更加复杂。因此,很有必要在一个较大的尺度上计算研究错动带对工程区渗流场造成的影响。
本文通过建立左岸三维有限元精细模型,以三维渗流理论为基础编写有限元计算程序,采用Zheng et al.(2005)建立的Signorini型变分不等式方法和改进的自适应罚Heaviside函数(陈益峰等, 2007)计算得到渗流自由面分布。针对山体内部定水头边界条件较难取值的问题,选择了5个典型勘察剖面来确定三维模型边界处的地下水位,再通过数值拟合的方法得到整个模型山体边界处的定水头值分布。研究了运行期白鹤滩电站左岸渗流场的变化规律和水力梯度场的分布,并对左岸地下厂区影响最大的C2错动带进行渗流场分析,评价错动带内渗透破坏的可能性。在施工设计图基础上对防治措施进行模拟计算,分析了置换洞和加强帷幕的防渗阻水效果。
1 三维有限元计算模型
1.1 三维稳定流数学模型
三维稳定流控制方程和边界条件如下:
有限元离散后,求解渗流场的线性方程组为:
[G][H]=[F]
(2)
式中,[H]为水头矩阵;[F]为已知的右端项;[G]为总导水矩阵(传导矩阵)。
渗流自由面求解的方法有:初流量法(张有天等, 1988)、剩余流量法(Desai et al., 1983)、截止负压法(张乾飞等, 2005)、压力扩展法(吉恩跃等, 2018)等,本次研究采用Signorini变分不等式方法求解(陈益峰等, 2007),与上述方法相比较,它可以更准确地求出溢出点,使得数值计算更加稳定。
1.2 模型精细剖分
白鹤滩水电工程主要由混凝土双曲拱坝、二道坝及水垫塘、泄洪洞、引水发电系统等建筑物组成。白鹤滩双曲拱坝坝顶设计高程834im,顶宽13im,最大底宽72im,上游正常蓄水位825im,坝高289im,建基面最低高程545im。选取大坝上游左岸一点(27°12′51.00″N, 102°54′09.00″E)作为坐标原点,取x轴指向正东,y轴指向正北,z轴垂直指向上的坐标系作为计算坐标系。
根据坝区工程地质和水文地质条件、水工建筑物布置方案,C2、C3层间错动带仅在左岸位置对地下厂房产生直接影响,因此选择左岸作为研究区。对三维有限元模型计算区域概化如下:上游边界取至导流洞洞口,距大坝900im; 下游边界取至3号交通洞洞口,距大坝1700im; 上下游边界顺河流向长度为2600im; 左岸边界取至距河流轴线1600im处山体内; 地表面作为上侧边界; 下侧边界取至大坝坝体主防渗帷幕底线高程440im以下140im处的相对隔水层位置(高程300im)。
左岸有限元模型采用空间八节点六面体进行离散,根据岩体和结构面渗透性分区,将研究区地层划分了12层,剖分成330i925个节点和1i887i036个单元,三维有限元模型及剖分见图 1。左岸模型考虑的主要结构面包括LS331、LS337层内错动带,C2、C3、C3-1层间错动带,F13、F17断层等(图 2)。模型还考虑了左岸地下厂区的水工建筑以及相应的防渗排水系统,其中地下厂区引水发电系统包括8条引水管、主厂房、主变洞、尾水调压室和4条尾水隧洞; 防渗排水系统包括抗力体排水洞和厂坝区的防渗帷幕、排水廊道,各结构布置如图 3所示。
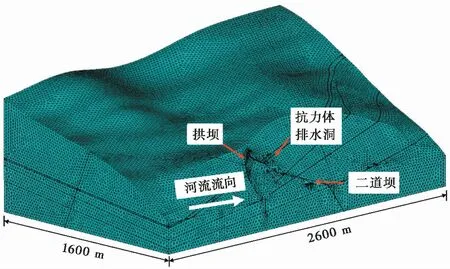
图 1 左岸三维有限元模型剖分图Fig. 1 3D finite element model of the left bank
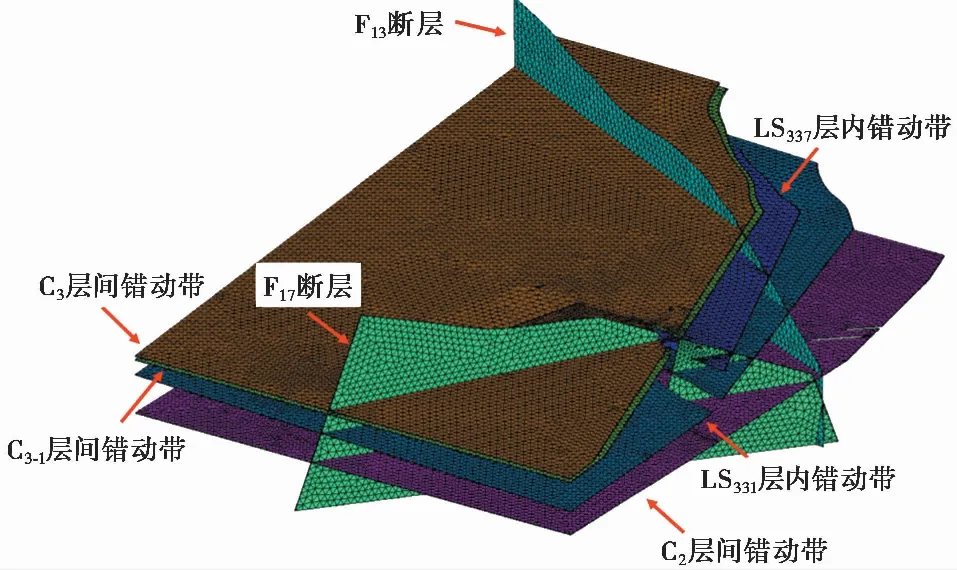
图 2 左岸模型主要结构面空间示意图Fig. 2 Main structural planes in the left bank model
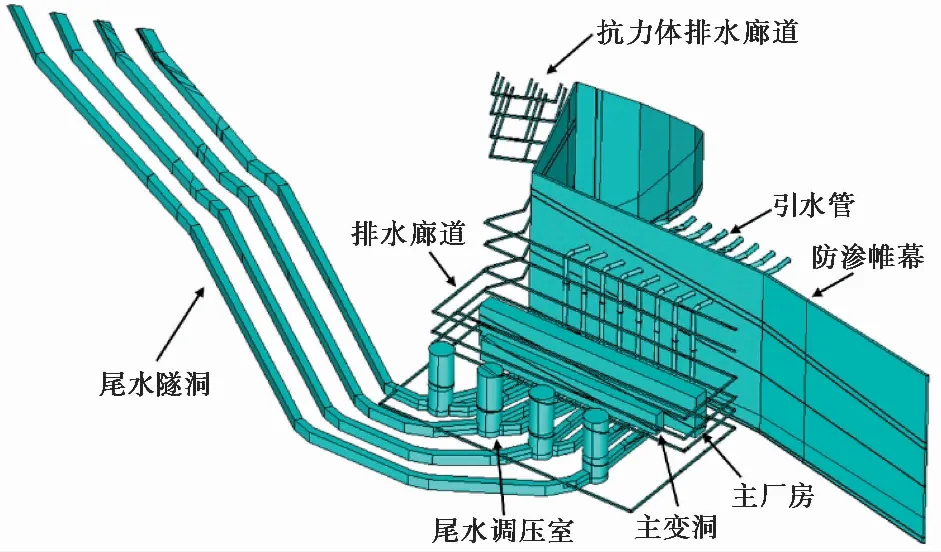
图 3 左岸模型地下厂区水工建筑与防渗排水系统布置图Fig. 3 Constructions and seepage control system of the underground powerhouse
1.3 渗透参数的确定
岩体内的结构面通常成组发育,渗透性表现为明显的各向异性,需要用渗透张量K表征。若取直角坐标系的3个轴Ox、Oy、Oz分别为正北、正东和铅直方向,则岩体渗透张量可以根据裂隙面法向单位矢与坐标轴的夹角余弦和裂隙面产状(倾向β、倾角γ)来确定(周志芳, 2007)。
(3)
式中,K为岩体的渗透张量;Kei为裂隙组的当量渗透系数;i为第i组裂隙的编号;n为岩体中裂隙发育的总组数;βi为第i组裂隙的倾向;γi为第i组裂隙的倾角。
根据地勘资料和现场试验成果确定模型内各地层与防渗排水结构的渗透参数。其中,各岩层、大坝混凝土和防渗帷幕为各向同性,渗透张量只取主轴方向。一般情况下,水泥灌浆形成的防渗帷幕渗透系数可以达到1.00×10-5cm·s-1,超细水泥或化学灌浆可以达到1.00×10-7cm·s-1。考虑到岩体本身渗透性较小(表 1),另外大型水利工程对防渗帷幕灌浆质量要求高,故选择防渗帷幕渗透系数为1.00×10-7cm·s-1。错动带与断层为各向异性,根据结构面的产状计算得到渗透张量的值。模型材料分区与渗透张量取值如表 1所示。
1.4 边界条件确定
三维模型的稳定渗流计算需要确定以下3种边界条件:
(1)隔水边界:上游边界和下游边界定为零流量隔水边界; 底部边界为隔水层底板,也作为隔水边界; 引水隧洞垂直段、下平段和尾水隧洞作为隔水边界。
(2)潜在溢出面(Signorini型)边界:厂区内主厂房、主变洞和尾水调压室,以及除最底层排水廊道外的其他排水廊道作为潜在溢出面边界。
(3)定水头边界:拱坝上游库水淹没区、上游蓄水位以下的表面节点作为定水头边界,水头为正常蓄水位825im; 拱坝下游河道、水垫塘、二道坝等在正常水位以下的表面节点作为定水头边界,水头为正常未蓄水水位(下游水垫塘水位)590im; 厂区、坝基和抗力体最底层排水廊道取定水头边界,水头值为该层排水廊道底部高程。
左岸山体边界拟作为定水头边界,然而此边界位于山体内部,没有长观孔的监测资料来确定该边界处的地下水位,可以通过5个勘察断面已有的水位资料分别计算得到该断面山体边界处的水头。此外,受蓄水后上游库水补给地下水和地下厂区防渗排水系统的排水影响,在给左岸山体定水头边界赋值时,不宜简单地赋一个定水头平均值。先利用长观孔的水位资料代入回水公式确定分水岭处的地下水位,再将选取的勘察线剖面作为典型剖面,利用COMSOL软件进行二维数值模拟,得到各勘察线所对应的三维模型边界处的地下水位,再利用MATLAB软件将各点拟合,得到左岸山体边界处地下水位分布情况。
根据现有资料,左岸地表分水岭为位于金沙江以西约5ikm的依果梁子。不考虑降雨入渗的影响,以库岸处金沙江水位590im的点为基点,选择5个勘察断面与该断面上长观孔的地下水位作为各已知点,求出分水岭处的地下水位值。勘察线位置示意图与计算结果如图 4所示。
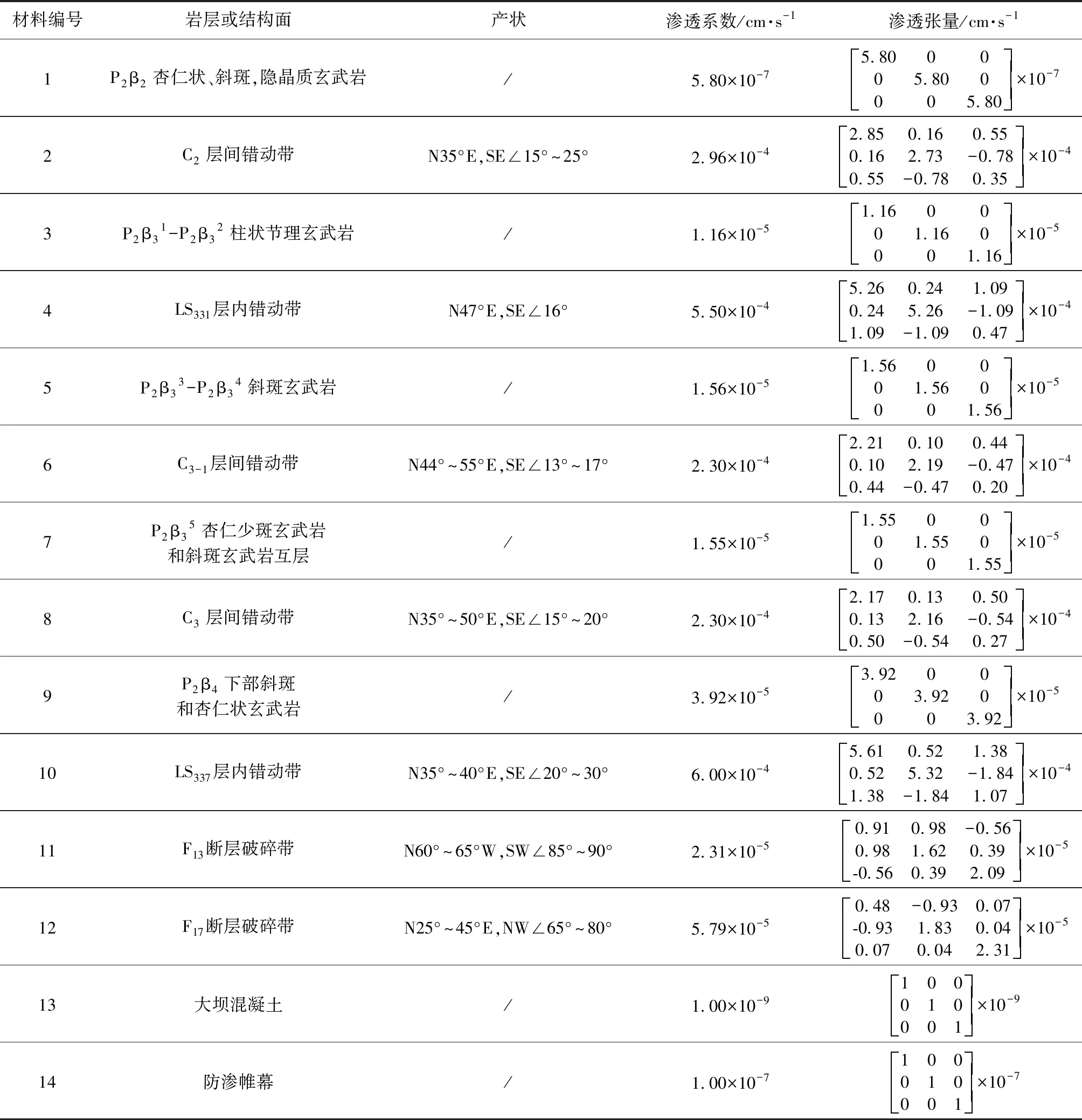
表 1 左岸渗透系数分区取值表Table 1 Values of seepage coefficient of the left bank
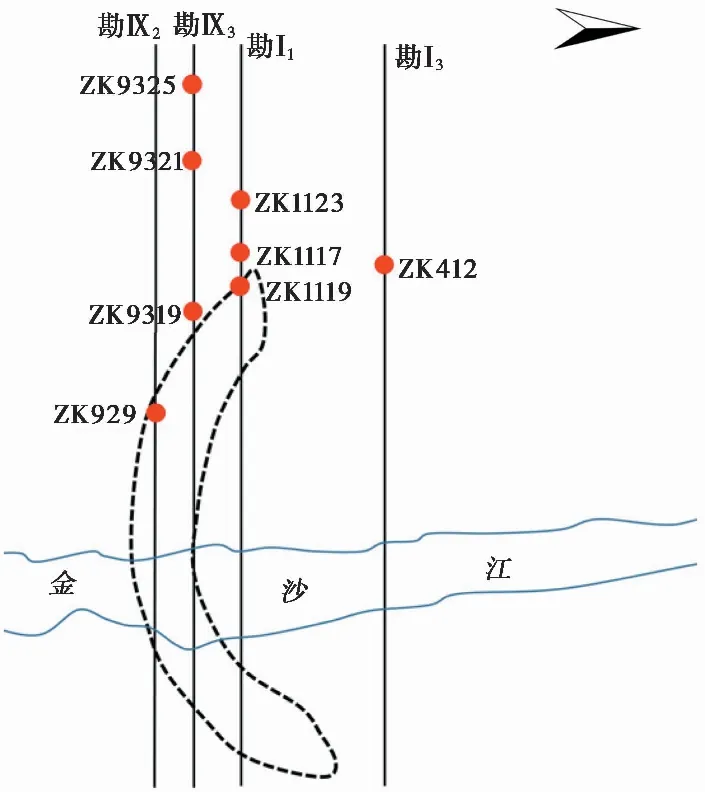
图 4 左岸勘察线分布示意图Fig. 4 Survey lines in the left bank

表 2 左岸代表断面山体边界处地下水位汇总表Table 2 Calculated values of the groundwater level in mountain boundary
根据各钻孔地下水位计算出来的左岸分水岭处地下水位值大致在1500im与1600im之间,取平均值1575im作为分水岭处定水头边界值。选取模型上、下游边界断面、勘IX3断面、勘I1断面和勘I3断面作为典型断面,利用COMSOL软件建立二维有限元模型,计算蓄水前后该断面的渗流场。最终得到各断面在山体边界处的地下水位,汇总如表 2所示。
将表2中与上游断面的距离作为Y轴,各断面山体边界处的地下水位作为Z轴,在MATLAB中采用分段3次Hermite插值多项式(PCHIP)方法进行拟合,得到左岸山体边界处地下水位,如图 5所示。

图 5 左岸山体边界地下水位Fig. 5 Groundwater level of the left mountain boundary
从图 5中可以看出,左岸山体边界水位在700im至900im之间。水库蓄水后上游受库岸一侧水位抬升,边界处水位增加,较未蓄水前水位增加约20im。厂区位置处受施工期降水的影响,边界处水位较低,与蓄水后边界水位相比最大可降约140im。将此地下水位分布作为定水头条件边界带入三维模型中计算。
2 渗透破坏预测
水库蓄水后,排水系统发挥降水作用,上游库水补给地下厂区,可能导致穿过厂区的错动带内部分区域水力梯度较大。较大的水力梯度是造成渗流破坏的原因之一(Chu-Agor et al.,2008),可以结合现场高压压水试验数据,确定错动带的容许水力梯度作为判断是否发生渗透破坏变形的标准,并对现有渗控措施进行评价。
2.1 容许水力梯度确定
渗流场中水力梯度变化大的区域可能会出现非线性流状态,这一状态会直接影响岩体的渗透破坏参数取值,错动带广义非线性流Forchheimer方程为:
J=av+bvm
(4)
其中,J为错动带水力梯度;v为渗透速度;m为非线性参数;a、b为非线性流渗透参数;a=1/K,K为错动带线性流(Darcy流)情况下的渗透系数。
在C2错动带进行现场试验的钻孔为CZK51,该孔完成了微水试验和低水头注水试验,得到C2错动带线性流情况下的平均渗透系数值为6.53×10-2cm·s-1,则非线性渗透参数a的取值为15.31is·cm-1。
在完整井流条件下,由方程(4)得:
(5)
式中,M为错动带透水介质厚度;Q为压(注)水试验时压水稳定流量;r为以试验孔轴心为原点的径向距离;H为以试验孔轴心为原点、半径为r处的水头。
由式(5)方程积分后可以求得b:
(6)
根据现场试验数据带入式(6)计算得到非线性系数b,结果如表 3所示(周志芳等, 2020)。
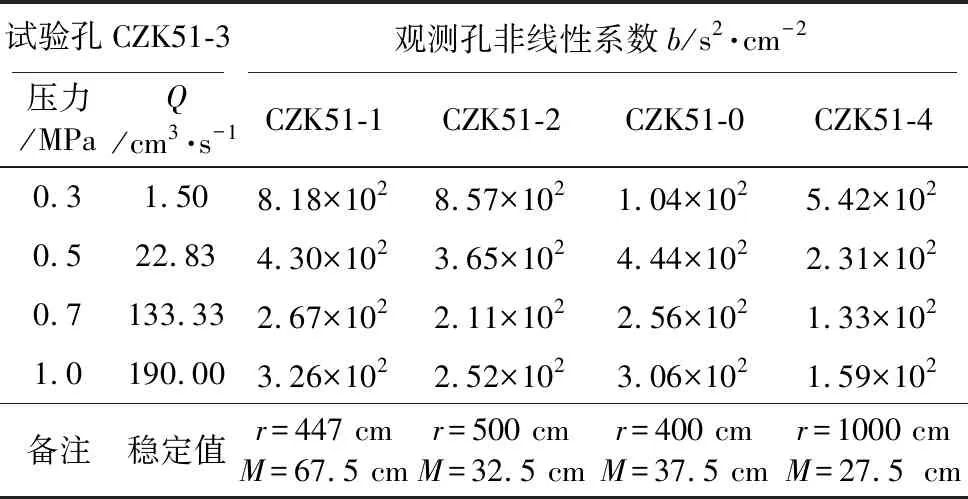
表 3 C2错动带非线性系数b计算表(m=0.5)Table 3 Calculation results of non-linear coefficient b of the interlayer staggered zone C2 (m=0.5)
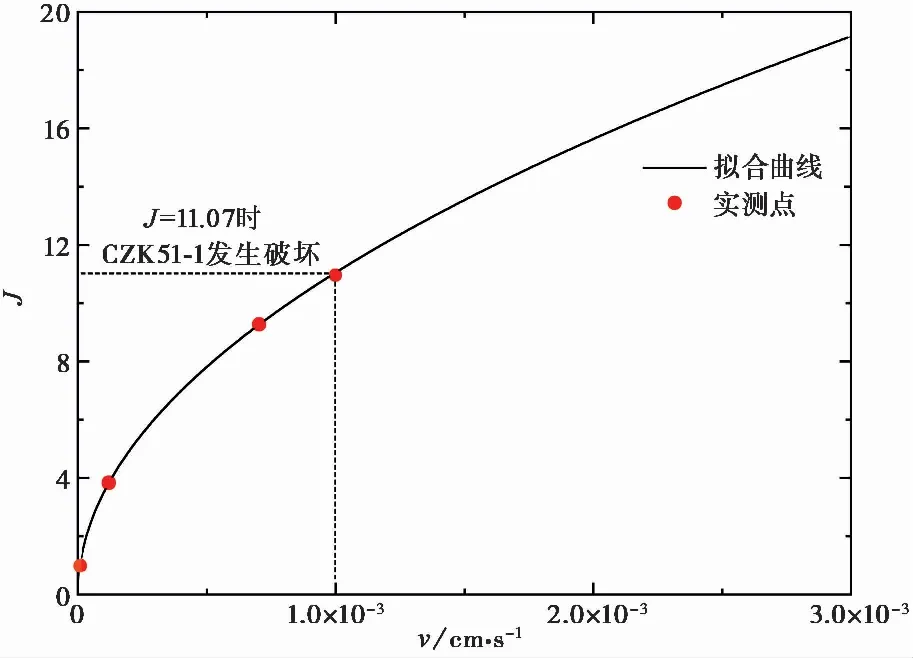
图 6 C2错动带水力梯度随流速变化曲线Fig. 6 Variation curve of hydraulic gradient with flow velocity in the interlayer staggered zone C2
根据上表求得C2错动带非线性系数b统计平均值为3.49×102is2·cm-2。将非线性参数a和b代入式(5)中,可以得到C2错动带水力梯度随地下水流速的变化关系曲线(图 6)。可以看出,在试验阶段错动带的水力梯度随地下水流速的变化呈明显的非线性关系,当流速为1×10-3cm·s-1时观测孔CZK51-1发生破坏,此时的J为11.07,即为C2错动带的破坏水力梯度。临界水力梯度或破坏水力梯度除以安全系数(2~3倍)可以确定容许水力梯度(彭土标, 2011),已知破坏水力梯度情况下安全系数取大值,因此C2错动带的容许水力梯度为3.69,临界水力梯度为7.38。
2.2 现有渗控措施评价
运行期地下厂区剖面等水头线分布如图 7所示。靠近库岸一侧渗流自由面经过防渗帷幕后受排水廊道的排水作用后急剧下降,在主厂房边墙底部溢出; 山体一侧自由面穿过尾水调压室后降至主厂房边墙底部溢出; 主变洞在自由面之上,不会发生渗流溢出。由于层间错动带渗透系数大于周围岩体,且垂向隔水、水平向导水,可以明显看出渗流自由面在结构面相交处发生起伏和弯折。在防渗灌浆帷幕和围绕厂区的7层排水廊道前阻水后排水作用下,坝区流向厂区的地下水渗流自由面逐渐降低,特别是在防渗帷幕后自由面有显著的降低。这是因为防渗帷幕渗透系数远小于C2错动带与C3-1错动带之间玄武岩体的渗透系数,防渗帷幕对降低地下水位起主导作用。渗流自由面在帷幕后进一步降低,说明排水系统发挥了作用,但由于该处岩体渗透系数较大,排水系统降水能力低于防渗帷幕阻水能力。防渗帷幕底部等水头线密集,与其相交的一段C2错动带内水力梯度较大。测得图中帷幕左侧错动带内最大水力梯度为6.72,超过了容许水力梯度,可能会发生渗透变形,而右侧水力梯度较小,为0.42。

图 7 地下厂区剖面等水头线图Fig. 7 Result of the water head isolines of the section of the underground powerhouse
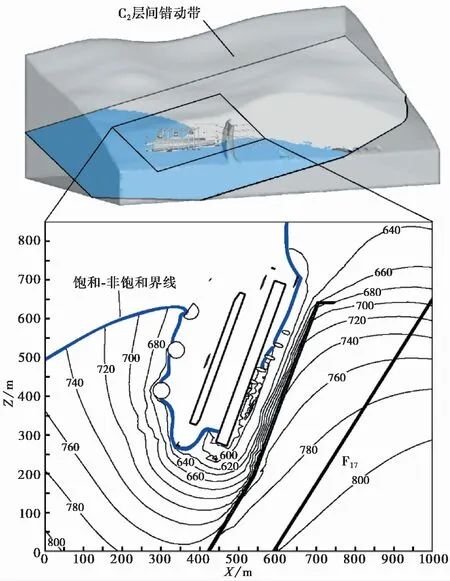
图 8 左岸C2错动带剖面等水头线图Fig. 8 Result of the water head isolines of the section of the interlayer staggered zone C2
由图 7可以看出C2错动带部分区域等水头线密集,水力梯度较大,有渗透破坏发生的可能性,故选取C2错动带作为特定结构面进行分析,水库正常运行工况下左岸C2层间错动带剖面渗流场分布如图 8所示。可以看出,渗流自由面位于主变洞之下,在主厂房底部和尾水调压室周围溢出。在防渗帷幕和厂区排水廊道共同作用下,防渗帷幕的厂房一侧等水头线密集,地下水位明显下降,说明防渗排水系统效果良好,帷幕靠厂房一侧水力梯度经测得最大可达6.91,需要采取一定措施防止因水力梯度过大而发生渗透变形。
3 防治措施模拟
截渗洞和截渗井等工程处理措施可以有效提高防渗效果,保证厂房安全稳定运行(熊平华等, 2017)。在施工设计图基础上对这一防治措施进行模拟计算,评价该措施防治效果。
截渗洞与加强帷幕根据施工通道布置在防渗帷幕靠近库岸一侧,截渗洞高4.5im,宽4im,垂直穿透C2错动带,加强帷幕施工结束后截渗洞内部回填膨胀素混凝土; 加强帷幕设计深度为10im。首先考虑增加截渗洞后防渗帷幕底部区域的渗流场情况。
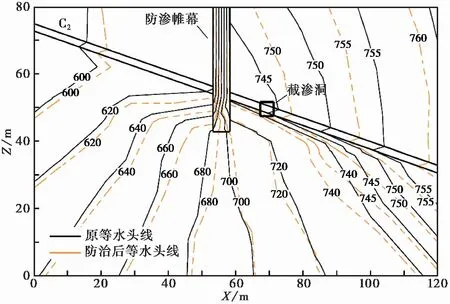
图 9 增加截渗洞后防渗帷幕底部等水头线对比图Fig. 9 Comparisons of equal head line at bottom of anti-seepage curtain after adding cutoff hole

图 10 设置10im加强帷幕后防渗帷幕底部等水头线对比图Fig. 10 Comparisons of equal head line at bottom of anti-seepage curtain after setting 10im reinforced curtain
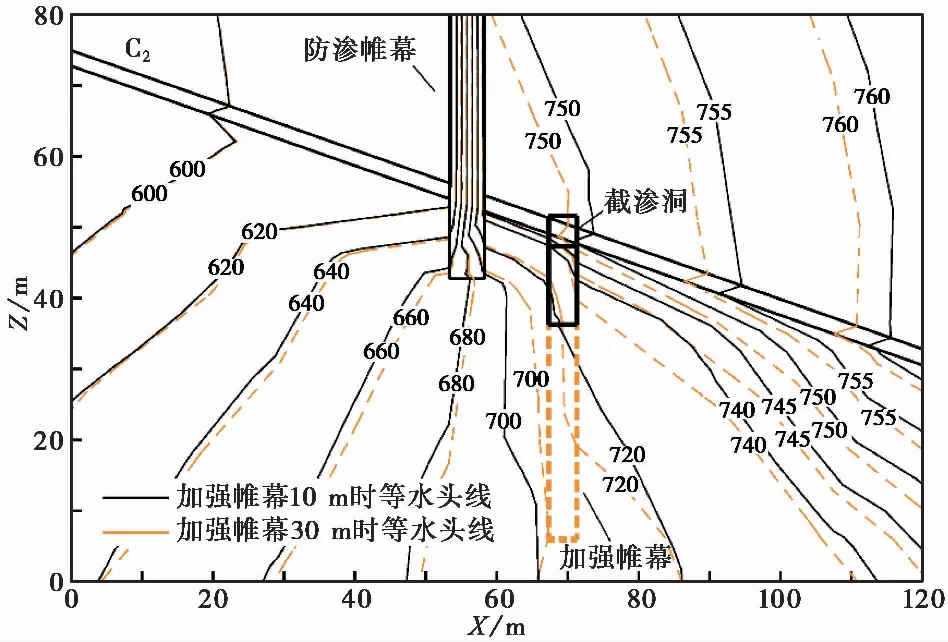
图 11 设置10im与30im加强帷幕等水头线对比图Fig. 11 Comparisons of equal head lines after construction of 10im and 30im reinforced curtains
若只在靠近库岸一侧设置截渗洞并完工后对其灌浆封堵防治前后防渗帷幕底部等水头线分布如图9所示。可以明显地看出截渗洞可以进一步阻挡水库一侧来水,截渗洞下方等水头线密集。靠近库岸一侧错动带内水力梯度明显降低,降至0.31。而位于厂房一侧地下水等水头线较未设置截渗洞前稀疏,错动带内水力梯度明显降低,降至0.59。设置截渗洞后可以有效降低错动带内水力梯度,不易在错动带内形成渗漏通道,但是截渗洞底部等水头线较为密集,水力梯度较大,需要进一步采取措施防止洞底部发生渗透变形。
若在截渗洞下方设置10im加强帷幕,防治前后防渗帷幕底部等水头线分布如图10所示。可以看出截渗洞可以进一步地阻挡水库一侧来水,截渗洞与加强帷幕附近等水头线较上一种情况稀疏。靠近库岸一侧错动带内水力梯度为0.38。而位于厂房一侧地下水等水头线变化不大,水力梯度为0.60。在设置截渗洞后基础上增加10im的加强帷幕主要降低截渗洞周围的水力梯度,而错动带内水力梯度分布与上一种情况大致相同,不易在错动带内形成渗漏通道。
将加强帷幕长度加长至30im,讨论加长前后等水头线分布, 如图11所示。与10im深的加强帷幕相比,增加至30im深后,靠库岸一侧等水头线更加稀疏,且阻水效果更加明显,错动带内水力梯度为0.47。帷幕靠厂房一侧等水头线分布差别不大,错动带水力梯度为0.57。该情况下错动带内水力梯度略有增加,但远小于容许水力梯度,不易因水力梯度太大而在错动带内形成渗流通道,保障厂区渗流稳定。
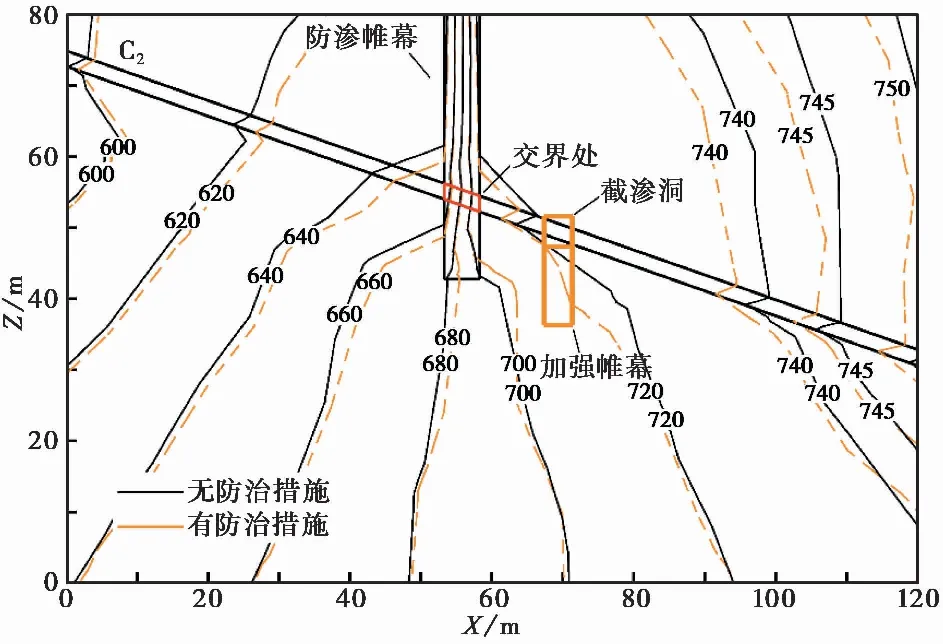
图 12 防渗帷幕失效时底部等水头线对比图Fig. 12 Comparisons of head line at bottom when impervious curtain fails
讨论防渗帷幕灌浆质量较差或防渗帷幕局部失效时设置加强帷幕情况下的渗流场,有无采取防治措施时等水头线分布如图12所示。该情况将交界处渗透系数定为1×10-5cm·s-1进行模拟。未采取防治措施时帷幕附近等水头线较为稀疏,说明可能在错动带内形成了渗漏通道,而加入截渗洞与加强帷幕后等水头线变得密集,体现出截渗洞和加强帷幕阻水的作用。两种情况下厂区一侧错动带水力梯度分别为1.80和2.44; 库岸一侧错动带水力梯度分别为0.74和1.10。模拟得到的水力梯度皆小于容许水力梯度,保障厂区渗流稳定。
4 结 论
(1)实现了对复杂地质、水文地质条件和复杂建筑物、帷幕、排水系统精细化模拟,展现了地下厂房、错动带、帷幕、排水系统渗流、水力梯度的空间变化规律。结果表明现有的防渗措施可以很好地发挥防渗帷幕的阻水作用和厂区排水廊道的排水作用,防渗排水效果良好。防渗帷幕与C2错动带交界处灌浆质量越好,其阻水效果越好,但阻水可能导致交界处周围水力梯度较大,可能在部分区域发生渗透变形。
(2)提出了通过山体边界水头值插值的方法确定无观测资料的山体边界水头值,可以更真实地反应出受水库蓄水和地下厂区防渗排水系统影响下山体边界处的水位,使得模型后期三维计算得到的结果更加符合实际情况。
(3)模拟预测结果证实,防渗帷幕前置截渗洞和加强帷幕可以有效截断渗漏通道,增加加强帷幕深度可更好发挥帷幕的阻水作用; 若帷幕局部失效,设置截渗洞和加强帷幕可以一定程度发挥阻水作用,保证地下厂房周围的渗流稳定。

