高陡岩质斜坡的结构面非接触式采集技术与三维裂隙网络模拟研究*
张 文 韩 博 孙昊林 陈浚淇 王硕男 孙 琦 尹 韩
(吉林大学建设工程学院, 长春 130012, 中国)
0 引 言
高陡斜坡常以岩体为主要载体,故充分认识岩体的物理、力学与变形性质是开展高陡斜坡分析的关键。由于结构面的强度较岩石小得多、变形大的多,岩体的变形破坏主要取决于其内部的结构面系统(谷德振, 1979)。因此,了解、认识并掌握结构面系统的展布情况是提高岩体工程分析精度、决定工程成败的关键。但实际上,岩体结构面常是难以全面获知的,甚至是难以窥探的(贾洪彪等, 2008)。目前来说,主要存在两个方面的难题:(1)高陡岩质斜坡露头面尺寸较大,往往近百米甚至几千米。而人工可调查区域相比甚小,仅若干米(往往1~2 m),远不能达到反映特大窗口结构面特征的需求(谢韬, 2011); (2)以现今的技术手段,结构面系统(长大结构面除外)的三维展布框架是不可视、不可知的,致使岩体工程的三维精细模拟与计算路途坎坷、任重而道远(黄润秋等, 2004; Stephanie et al.,2018; Li et al.,2019)。针对这些问题,我们认为岩体结构面获取技术与三维结构面推导理论的发展与创新是跨越岩体工程定性-定量分析鸿沟的关键一步。故本文从上述两个问题展开具体阐述与研究。
岩体结构面的尺度跨越若干数量级,由几毫米至几百公里不等。故结构面的采集、认知及其作用是随尺度而变化的。Ⅰ~Ⅲ级结构面是区域与工程尺度的反映,其展布特性具有一定程度的可视性与可推测性。除传统采集方法外,遥感分析等技术近年来不断用到这些大型结构面的识别上(董秀军等, 2019); Ⅳ级结构面是工程尺度的反映,会影响到斜坡的整体稳定性与局部(块体)稳定性(杜时贵等, 2017)。传统的采集与模拟技术主要集中在小窗口结构面数据上(Han et al.,2016)。近年来,三维摄影测量、数字近景摄影测量与无人机技术等非接触式结构面采集方法已初步运用到Ⅳ级结构面的识别中(Roberts et al., 2003; Abelln et al., 2006; 董秀军等, 2006; 王凤艳等, 2012; Gregory D et al.,2016; 葛云峰等, 2017; 李水清等, 2017; 张骞棋, 2018; 刘子侠等, 2019)。但总体而言,这些非接触式采集式技术仍不成熟,工程应用较少,待于推广。
为进行岩体工程的三维精确分析,推演结构面的三维展布情况是岩体计算、模拟与分析所必需的。如上述,大型结构面可根据其产状等特性推测其空间展布形态; 而对于构造随机结构面系统(Ⅳ级结构面)则必须采用三维裂隙网络模拟来实现统计意义上的表征与刻画。传统意义上,岩体三维裂隙网络模拟针对小窗口结构面数据,采用统计均质区划分、优势分组、产状校正、迹长校正、直径推算、密度推算、网络模型生成与结果验证等若干步骤(Palleske et al.,2013; Han et al.,2016; Bauer et al.,2017)。近几十年来,众多学者针对这些步骤进行了数学意义上的推算,已相对纯熟、全面。但针对高陡斜坡大窗口采集的结构面数据的模拟工作仍缺乏一定的研究与运用,亟待理论的突破。
针对以上问题,本文聚焦高陡斜坡超大窗口上的结构面系统,采用非接触式采集方法获取岩体结构面系统,并建立针对大窗口随机构造结构面数据的三维裂隙网络模拟方法。
1 工程实例
本文以阿坝藏族自治州汶川县绵虒镇境内的大溪沟斜坡为研究对象。大溪沟地处汶川县东北部,距汶川县城13.8 km。沟内地形较陡峭,斜坡坡度多为50°以上。
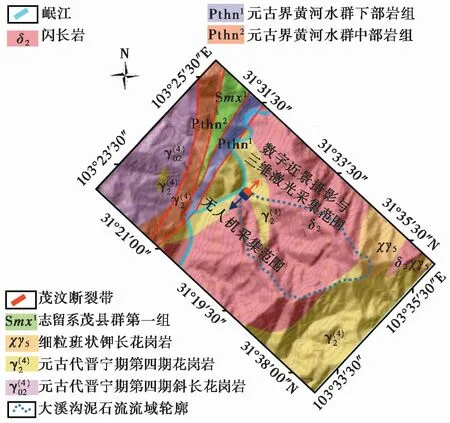
图 1 大溪沟及其沟口斜坡位置与基本地质信息图Fig. 1 Location and geological information of Daxigou gully and its slopes
研究对象(大溪沟斜坡)位于大溪泥石流沟的左岸(图 2),斜坡的总体地势为东北低西南高,坡高100~160 m。斜坡陡峭,坡面有植被发育,常顺长大结构面延展。斜坡露头面分为两段,上游段长约90 m,坡面产状为27°∠66°; 下游段长约120 m,坡面产状为95°∠67°。坡面被庞大且复杂的节理裂隙所切割,存在很多潜在的不稳定块体。
如图 2,在坡形转折点上游坡面上可见部分岩体表面风化严重,风化物厚2~3 cm,呈灰褐色。推测早期有较宽的结构面(如后缘拉张裂隙)在此出露,水通过结构面运移,不断侵蚀结构面两侧的岩体,使其发生了较为强烈的风化。在坡形转折点下游坡面上可见擦痕,擦痕方向指向沟谷下游(NNE)。在坡底可见一长大缓倾结构面(倾向NNE,倾角约25°),内部充填岩石碎屑,为岩体中的软弱结构面。根据以上调查结果,可推测上游坡面为一老滑坡后缘破裂面,下游坡面为老滑坡左边界破裂面,缓倾结构面为老滑坡滑动面。出露的斜坡即为老滑坡滑动后所残留的后方与边界处的坡面。

图 2 大溪沟斜坡现场照片与滑坡边界调查信息图Fig. 2 Site photos of Daxigou slopes and their boundary information
2 结构面采集与裂隙网络模拟
传统人工测量的方法仅能采集坡脚处的个别结构面,无法获取实例中一百多米高窗口上的结构面整体特征。为实现结构面系统全面的识别与采集,我们引入非接触采集设备,即三维激光扫描仪、近景摄影测量与无人机来采集坡面地形及其表部发育的复杂结构面系统。采用上述方法可较为方便地获取高陡斜坡坡面超大窗口的结构面数据; 另外,本节针对这种结构面数据类型,介绍一种简单方便的三维裂隙网络模拟方法。具体简述如下:
2.1 非接触式数据采集
现场采用加拿大Optech的Ilris-lr型号三维激光扫描仪进行非接触式数据采集。这种技术通过大面积发射激光束获取被测物体表面的点云(三维坐标),可快速、大量地采集物体的三维影像模型,建立其DEM模型(白志华等, 2018); 采用佳能70D数码单反相机(定焦)配备焦距为EF 135 mm f/2L USM镜头进行数字近景摄影测量。这种技术通过叠加数字摄影的方式获取被测物体上各点的三维坐标,故可方便地建立物体的三维影像与精细DEM模型; 采用大疆精灵Phantom 4 RTK航测无人机。这种技术结合航拍摄影与机载遥感,建立被测物体的三维影像与DEM模型,适宜于大区域地质体的建模与解译。
三维激光扫描法适宜建立被测物体的三维坐标系统,其精度较高,通常能达到厘米级甚至毫米级,但受限于物体三维图像的分辨率,不宜进行精细图像(如结构面系统)的人工识别与解译。数字近景摄影测量方法现场操作步骤繁琐、效率较低,但镜头的分辨率较高,可获取清晰图像,利于人工识别与解译结构面系统。无人机建模速度快、区域大,有助于建立地质体的全局概念,进而解译其长大结构面系统。但受其图像分辨率的影响,不宜进行较小节理裂隙的识别与解译。
综合上述方法的优缺点。在岩体结构面信息获取时,可采用无人机识别与解译长大结构面信息; 采用近景摄影测量“人工识别”或三维激光扫描结合智能算法“自动识别”较小的节理裂隙。本文主要采用人工识别的方法获取结构面系统,故三维激光扫描技术仅用来获取坡面地形,不用来识别结构面。
针对以上非接触式方法的优缺点,我们采用无人机建立现场坡体的DEM模型,并建立宏观结构面的全局概念; 采用三维激光扫描法建立坡面的精细三维DEM模型; 采用数字近景摄影测量解译坡面的随机构造结构面系统。
2.2 大窗口三维裂隙网络模拟方法
三维裂隙网络模拟技术适用于内动力作用(构造应力)导致的构造结构面系统。除此以外,斜坡常出现由于外动力作用导致的卸荷裂隙与风化裂隙等,但这种结构面仅在坡表区域出露,一般不采用三维裂隙网络模拟方法进行分析。
通过以上方法,可确定长大构造结构面与随机构造结构面系统。长大构造结构面产状相对稳定,可通过延展推测的方式来确定坡体内部的长大结构面,故本节不将宏观结构面作为模拟的对象。但对于随机构造结构面,由于其数量庞大、产状随机,必须采用三维裂隙网络模拟的方法确定(贾洪彪等, 2002)。本文介绍一种适宜于大窗口三维裂隙网络模拟的方法,具体如下:
三维裂隙网络的模拟是基于圆盘假设的基础上进行的,即近似认为不连续面在空间上是一个薄圆盘(图 3)(宋晓晨等, 2004)。基于圆盘假设,三维裂隙网络模拟可从以下几个方面进行:(1)优势分组; (2)不连续面的大小模拟; (3)不连续面的产状及密度模拟。
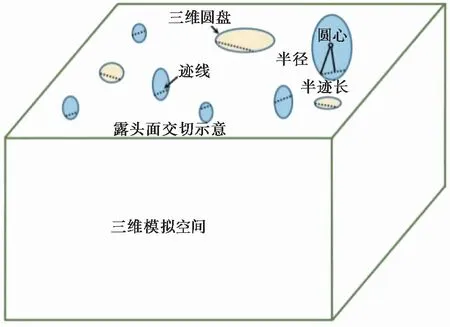
图 3 裂隙网络-迹线-露头面关系示意图Fig. 3 Relationship among fracture network, traces and outcrop surface
2.2.1 优势分组
为缩小岩体结构面的离散性,也为方便不同期次(特征)结构面几何特征统计规律的总结,需对岩体结构面进行优势分组。但是当结构面数目庞大、产状十分离散时,优势分组的结果常不合理,比如常会将对斜坡破坏作用不同的缓倾与陡倾结构面划分为一组。这里我们提出一种新的优势分组思想,即从宏观尺度(如采用无人机测量)确定结构面的组数与平均产状,继而判断各离散结构面与宏观结构面的产状距离d(宋腾蛟等, 2015)。以最短距离原则,将离散结构面划分至宏观结构面组,产状距离计算公式如下:
(1)
式中,α为结构面倾向;β为结构面倾角;θ为离散与宏观结构面的产状夹角;i为离散结构面序号;j为宏观结构面序号;d(Xi·Xj)为第i离散与第j宏观结构面的产状距离。
2.2.2 直径模拟
如上述,不连续面可采用薄圆盘来近似表述,故确定不连续面大小的过程就是确定直径服从的分布函数的过程。由图 3所示,半径r、半迹长ch及圆盘圆心至迹线的距离u之间满足勾股定理,如式(2)所示。
露头面与圆盘的交切位置是随机的,即圆心至露头面的距离u是服从0~r的均匀分布。可见,u/r服从(0, 1)的均匀分布。则由概率学可知,均值E(u/r)=1/2,方差D(u/r)=1/12。式(2)两边取均值,可推导得到式(5)的结果,即半径平方的均值为半迹长平方均值的1.5倍。
ch2+u2=r2
(2)
E(ch2/r2)+E(u2/r2)=1
(3)
E(ch2/r2)+E(u/r)2+D(u/r)=1
(4)
E(r2)=1.5E(ch2)
(5)
根据现场采集的裂隙迹长数据,可获取E(ch2); 随后即可按式(5)计算得到E(r2)。将r2视为未知函数,假设r2的概率密度分布函数与方差D(r2),可生成r2的随机数S1。由式(2)知ch2/r2=1-(u/r)2,通过生成u/r的均匀分布随机数,可生成ch2/r2的随机数S2。通过S1×S2操作即可得到ch2的随机数S3。通过试算法即可确定某一概率密度分布形式下,不同方差D(r2)下生成的S3是否可表征现场真实半迹长ch的分布情况,具体可采用卡方或KS检验来判别(Bryant et al., 2012)。另外,最终的概率密度分布函数也可采用上述非参数检验来判别,具体不再赘述。
通过上述操作,即可确定半径r的随机数(概率密度分布)。但值得一提的是,上述r仅为与露头面相交的三维结构面的半径。半径越大,圆盘与露头面相交的概率越大,实际三维空间内的圆盘平均尺寸要偏小。我们提出式(6)推导整个三维空间内不同裂隙半径范围(以下限a,上限b表示)的裂隙数分布情况。
(6)
式中,n′ab为与露头面相交的半径位于a与b之间的裂隙数;nab为三维空间内半径位于a与b之间的裂隙数;θ为裂隙平均产状的法线与露头面法线的夹角;L为露头面法线方向上三维空间的长度。
经过式(6)可以得到一组新的三维圆盘半径r的随机数,从而可确定不连续面直径实际满足的分布函数。
2.2.3 产状及密度模拟
岩体结构面产状常认为服从经验分布、Fisher分布与双正态分布等。本文充分考虑岩体露头面上测得的结构面产状,即采用经验分布来生成三维空间内的结构面产状(宋腾姣等, 2015)。由于现场实测产状频率往往扩大了与露头面呈大角度相交的结构面的频率,我们采用式(7)对该偏差进行校正。
(7)
式中,αi为第i产状区段与露头面的夹角;Nai为该产状区段对应的裂隙条数;Pi为该区段校正后的频率。
不连续面密度的模拟是通过试算法完成的,具体步骤如下: (1)假设裂隙总条数(可反映裂隙密度)为K,综合上述裂隙直径与产状,生成待用三维裂隙网络; (2)采用与露头面产状一致的平面截取此待用三维裂隙网络,确定与平面相交的裂隙数k; (3)如模拟露头面上的裂隙条数与实际露头面裂隙条数存在差距,则调整K值,直至k与现场测得的裂隙数一致。通过以上方法即可方便地获取裂隙网络的三维密度。
3 非接触式采集数据分析
3.1 无人机数据采集
本次航测的主要目的是对大溪沟斜坡宏观结构面产状进行解译,到达场地后首先进行大疆精灵Phantom 4 RTK航测无人机的组装、预热、校准指南针等工作,通过无人机地面控制站安装的GSRTK-APP现场定位,设定飞行区域及飞行参数,控制站依此自动规划了3条航线,采用自动拍摄的方式对斜坡进行图像采集(Gregory et al.,2016; 李水清等, 2017; 张骞棋, 2018)。本次拍摄共获得24张带有GPS坐标属性的航测照片,航向重叠率80%,旁向重叠率70%。将无人机拍摄的连续照片导入ContextCapture三维建模软件,建立实体三维数字模型。
在无人机建立的三维数字模型中可轻易识别出岩体中发育的宏观结构面系统,便于我们建立“岩体结构控制论”的整体概念(兰恒星等, 2019)。我们采用人工识别解译的方式,即人为选取结构面上不在同一直线上的n(n≥3)个点,选点时以结构面一端点作为起始点,沿结构面方向依次选择,至另一端点为止。则两端点间距离即为结构面迹长; 由选取的n点可确定一平面,利用平面空间方程可得其法向量,继而可进一步确定其产状(赵明宇等, 2018)。当摄影测量(包括无人机与数字近景)分辨率足够高或结构面属性较为明显时,可解译结构面的张开程度(或闭合)以及填充情况等关键信息。
由图 4所示,宏观结构面共呈现4组。第1、3、4组结构面均为陡倾结构面,产状分别为31.6°∠81.5°、102.2°∠75.5°与152.8°∠83.3°。其中,第1与第3组结构面分别与滑坡后缘与左边界破裂面产状相仿; 第2组结构面产状为0°∠29°,缓倾向下游,与现场调查的滑动面产状相似。这一方面证明了滑坡破裂面沿结构面扩展的“岩体结构控制论”,另一方面也验证了无人机解译结构面信息的准确性。
3.2 三维激光扫描数据采集
三维激光扫描主要用于解译斜坡坡面的空间位置信息(Abelln et al.,2006; 董秀军等, 2006; 葛云峰等, 2017)。对该岩质斜坡共扫描了3幅影像,两两影像之间有30%~40%的重叠度。叠加即可建立斜坡坡面上任一点相对于三维激光扫描仪器的坐标。其中,X与Y轴方向分别为三维激光扫描仪瞄准与垂直的方向,Z轴为高度方向。而这种坐标体系是不便于岩体进一步分析研究的,故我们将其转化为以X与Y轴为正东和正北方向下的方位坐标系,如图 5的4个坐标转换点所示(第1行为方位坐标系,第2行为三维激光扫描坐标系)。
通过带有空间位置信息的三维激光点云数据,可以生成该岩质斜坡的DEM数据。将其导入到ArcGIS软件中,即可采用3D Analyst中的功能获得斜坡坡面的倾向和倾角分布。在模型中,可清晰看到滑坡后缘破裂面与左边界破裂面的产状分布。

图 4 无人机获取的大溪沟整体影像与识别的宏观结构面Fig. 4 Overall image and recognized macro structures of Daxigou slopes using UAV
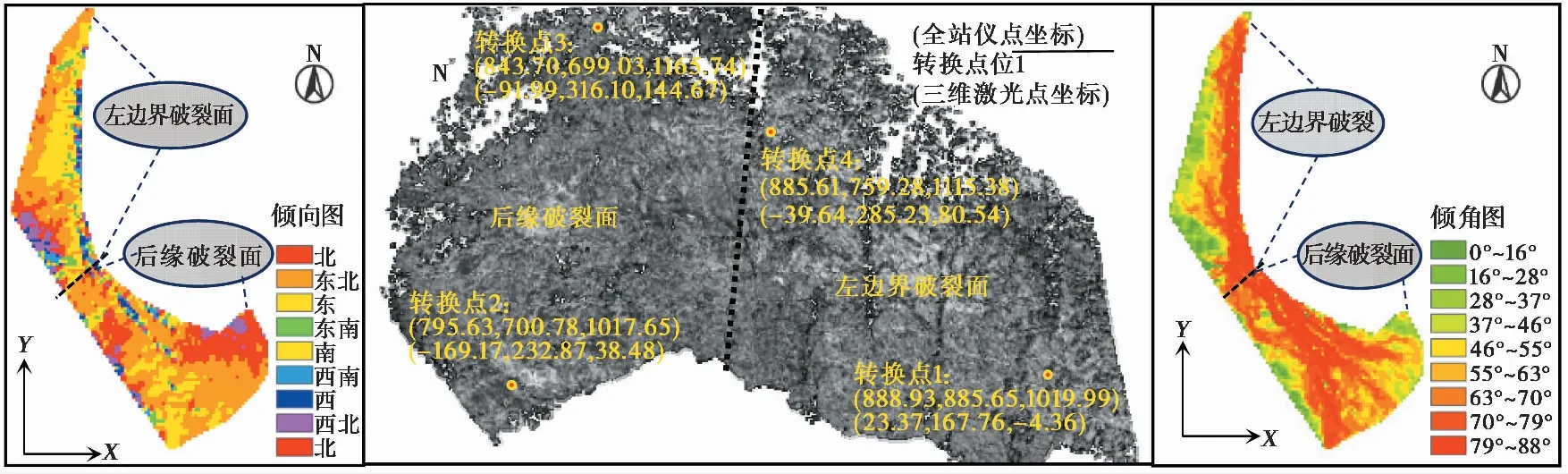
图 5 三维激光扫描仪获取的点云及坡面产状分布图Fig. 5 Point clouds and outcrop orientation distribution obtained with 3D laser scanner
两破裂面的倾向与倾角离散性较高,这是由斜坡表部块体破坏掉落而导致的。总体而言,后缘破裂面倾向N-NNE,平均坡度为66°; 左边界破裂面倾向E,平均坡度为67°。坡面精细DEM数据对三维裂隙网络的建立、验证与方法改进具有重要意义,具体如第5节所述。
3.3 数字近景摄影测量
沿近似平行于斜坡走向的方向上布设摄影基线,在基线上选取左右两个拍摄点,分别对同一岩体区域拍摄重叠面积在80%以上的左右影像。同时,测得左镜头的经纬度、高程以及镜头方位角和两个拍摄点的间距。采用VirtuoZo软件对左、右影像进行对应像素点匹配、影像合成并标定镜头坐标等即可构建所拍摄岩体表面的三维模型(Roberts et al.,2003; 王凤艳等, 2012; 刘子侠等, 2019),具体不再赘述。在三维模型上可清晰看到坡面上发育的结构面系统,结合其内置的空间三维坐标,即可确定结构面的产状与迹长等几何参数(图 6),具体可参照无人机解译原理,在此不再赘述。
现场可摄影场地受到极大限制。为保证结构面信息采集的准确性,拆分多个窗口进行分批次拍摄建模。如图 6所示,在滑坡后缘破裂面上共建立了4个模型解译窗口,即窗口1~4,共解译出2687条结构面,其节理玫瑰花与迹长概率密度如图 7a所示; 滑坡左边界破裂面上共建立了7个模型解译窗口,即窗口5~11,共解译出3976条结构面,其节理玫瑰花与迹长概率密度如图 7b所示。
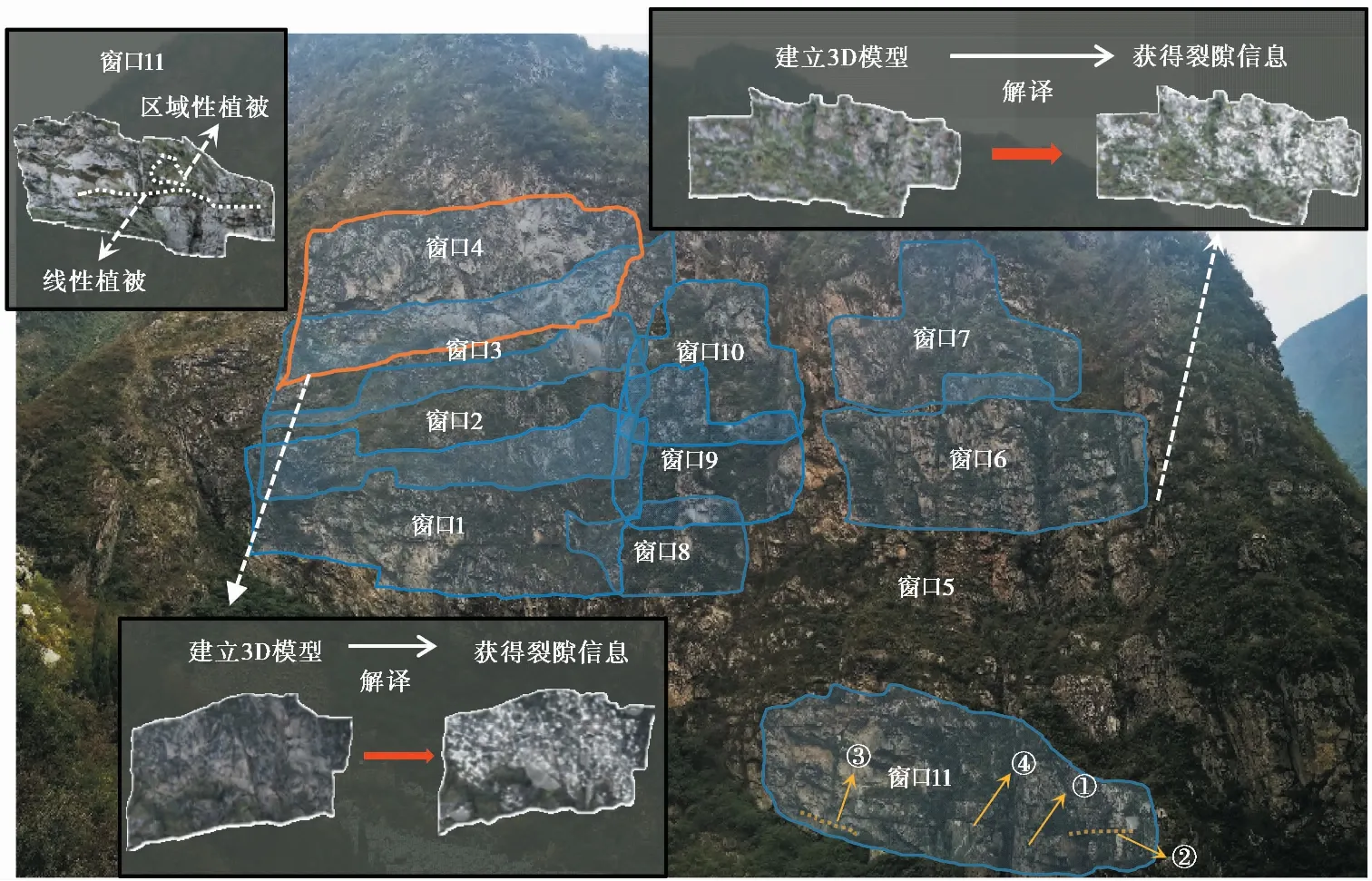
图 6 数字近影摄影测量窗口布置与模型解译示例图Fig. 6 Sampling windows and interpretation of models for digital close-range photogrammetry
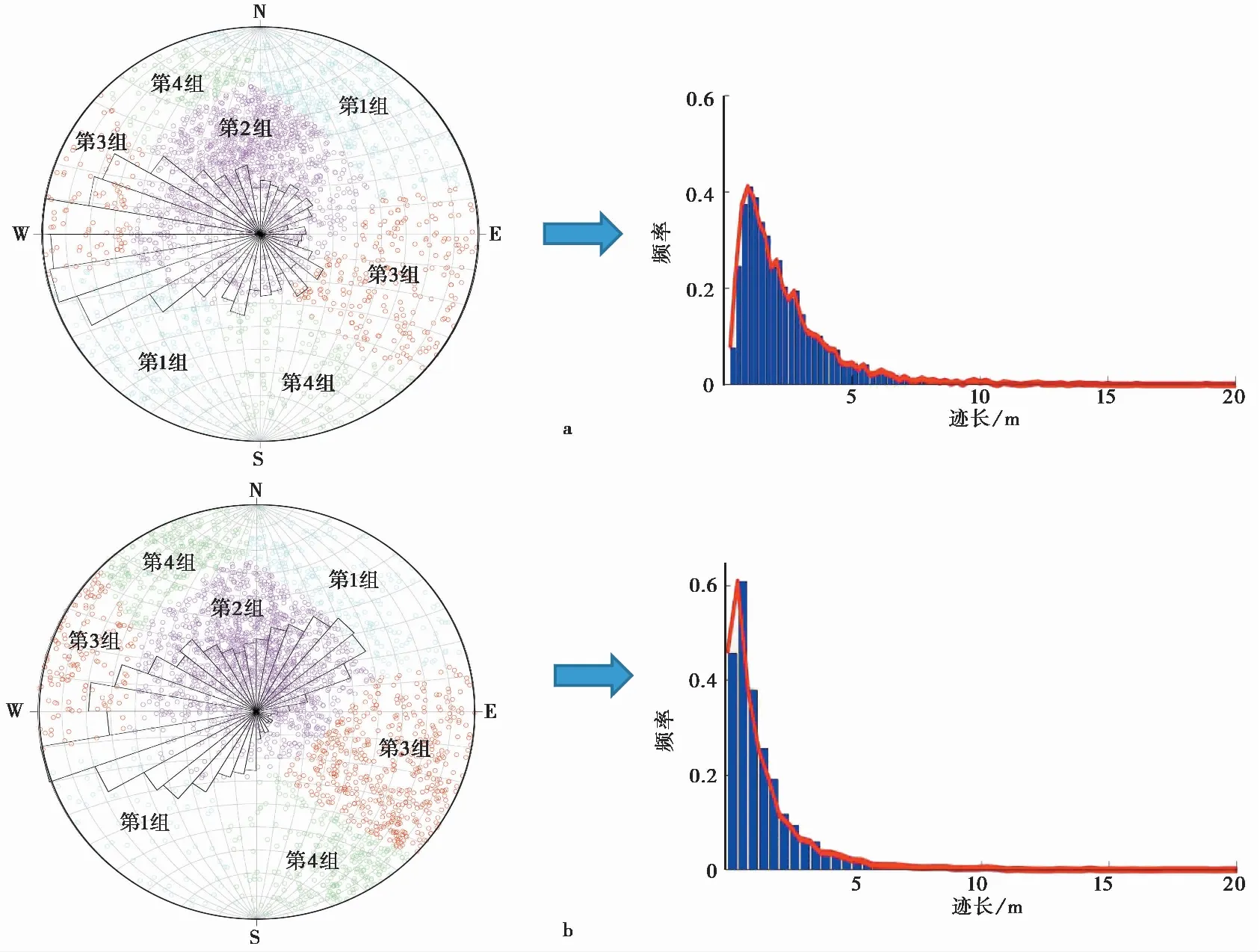
图 7 大溪沟斜坡坡面裂隙的节理玫瑰花图与迹长概率密度分布图Fig. 7 Rose diagrams and trace length probability density distribution of fractures in Dasigou slope outcropsa. 滑坡后缘破裂面上结构面描述; b. 滑坡左边界破裂面上结构面描述
对穿越不同窗口的节理裂隙进行合并处理。可见,由于摄影区域较大,最终可形成高陡斜坡结构面采集的超大窗口。在此窗口内绝大多数为两端可见的裂隙,不同于传统人工采集的裂隙数据。故大窗口数据对应的三维裂隙网络模拟理论应有所区别,应可较大程度上简化。
为验证数字近景摄影测量的可靠性,对窗口11坡脚处的4条裂隙进行人工测量,将实测与解译数据进行对比(图 6)。实测数据分别为128°∠75.8°、235.8∠25.7°、17.2°∠24.3°、275.4°∠78°,对应解译数据为124°∠87°、240°∠21°、7°∠30°、292°∠90°,可见两者基本一致。另外,植被覆盖是结构面分析的重要影响因素。线性展布的植被对结构面具有指示性,因为植被常沿张开度较大的结构面展布; 较破碎岩体或松散堆积处发育的区域性植被会覆盖结构面,导致这一区域的结构面无法解译,进而使现场采集结构面的数量和密度偏小。在无人机解译得到的宏观结构面的基础上,近景测量解译了大量无人机不能分辨的规模较小的随机结构面,为岩体随机结构面系统的分析提供了丰富的数据支持。
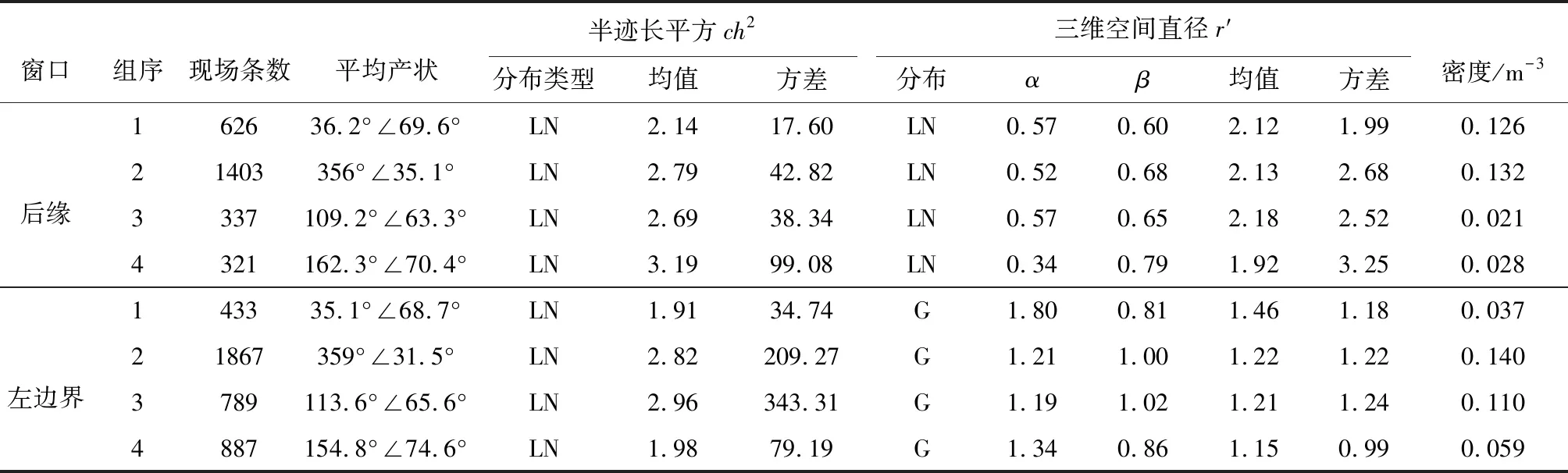
表 1 三维裂隙网络参数汇总表Table 1 List of 3D fracture network parameters
表中G表示Gamma分布,LN表示对数正态分布。对Gamma分布而言,α为形状参数k,β为尺度参数γ; 对对数正态分布而言,α为变量对数的均值,β为变量对数的方差
4 三维裂隙网络模拟及其结果
在生成三维裂隙网络之前,我们需确定容纳裂隙的三维空间大小。由三维激光扫描或无人机测量得知,滑坡后缘段和左边界段沿露头面走向的长度分别为90 m和120 m,露头面高分别为115 m和125 m。由于三维裂隙网络模拟具有一定的边缘效应,故需扩大尺寸进行分析。最终,滑坡后缘段的三维裂隙网络尺寸为170 m(X轴/南北向)×200 m(Y轴/东西向)×120 m(Z轴/铅垂向); 左边界段为230 m×150 m×130 m(图 8)。

图 8 后缘与左边界破裂段的三维裂隙网络显示 (不含宏观结构面)Fig. 8 Display of 3D fracture network for trailing and left edge areas(macro discontinuities are excluded)a. 后缘破裂段三维裂隙网络; b. 左边界破裂段三维裂隙网络
如第3节的三维裂隙网络模拟步骤所述,需首先确定与结构面交切的平面(露头面)产状。而如图 5的三维激光扫描精细DEM模型所示,坡面产状离散性较大,极大程度上增加了裂隙三维参数的推导与研究的难度,故我们通过取坡面平均产状的方法建立交切平面,简化三维裂隙网络的模拟步骤。滑坡后缘段和左边界段坡面产状差别较大,我们无法建立整体的三维裂隙网络,故需对其分别建立。
如第4节所述,通过近景摄影测量的手段,在现场测得了大量的裂隙数据。同时,利用无人机观察到坡体存在4组较为明显的宏观结构面。因此,我们采用第3节中介绍的优势分组方法,分别计算离散裂隙与宏观结构面的产状距离,进而确定了分组方案。各组的平均产状与裂隙数如表 1所示。
按照第3节中所述的方法,可方便建立两处坡面上裂隙的半迹长平方均值E(ch2)。表 1显示,各组裂隙的E(ch2)介于1.9~3.2之间; 通过式(5)可知,与露头面相交的裂隙半径平方均值E(r2)介于2.9~4.8之间。通过现场出露的迹长数据,采用试算法与非参数检验即可确定与露头面相交裂隙r的随机数。继而,可通过式(6)确定整个三维空间的裂隙直径。如表 1所示,后缘破裂段发育的各组裂隙直径服从对数正态分布,均值为2 m左右; 左边界破裂面裂隙直径服从伽马分布,均值介于1.1~1.5 m之间。
根据露头面上发育的裂隙产状,采用式(7)校正后,即可生成服从经验分布的三维空间裂隙产状分布。另外,采用产状与露头面平均产状一致的平面交切三维裂隙网络,即可采用试算法得到裂隙网络的三维密度。如表 1所示,不同坡段、不同优势组的三维密度均相差较大。
值得注意的是,对于不同坡度但相同优势组的裂隙来说,其裂隙直径与密度仍有较大差异。这说明了岩体结构面发育的非均匀性; 但也有可能是左边界破裂面上极不平整,掉落块体较多,导致较大结构面从中间断开,人为解译很难充分考虑这一物理地质现象。故左边界破裂面上推导的裂隙直径较小; 另外,由于块体掉落,与露头面近平行的裂隙极容易暴露在坡表,被解译到的可能性也急剧增大,这也就扩大了这组结构面的实测频率,如后缘破裂面上的第1组结构面和左边界破裂面上的第3组结构面。前述的两种情况给三维裂隙网络模拟理论提出了新的挑战,是未来的重要研究方向。
根据上述获得的三维裂隙参数,基于Monte-Carlo模拟随机组合以上参数即可生成三维裂隙网络(不同颜色代表不同优势组),最终如图 8所示。
为检验三维裂隙网络模拟效果,我们采用如图 8所示的坡面交切整个三维裂隙网络。记录三维裂隙面与坡面的交切迹长,与现场实测迹长进行对比,结果如图 9所示。我们可以看到,两者拟合程度较好,相关系数均在0.9以上,说明以上模拟过程得到的模拟迹长与现场迹长相符合,即证明了所建立的三维裂隙网络的合理性。
由图 8可见,三维裂隙网络模型能够直观地反映岩体内部结构面的展布情况,有助于岩体三维结构参数如体积节理数的计算,进而为岩体工程分级提供依据。根据岩体分级结果可半定量地确定内摩擦角、黏聚力、变形模量及泊松比等岩体参数。
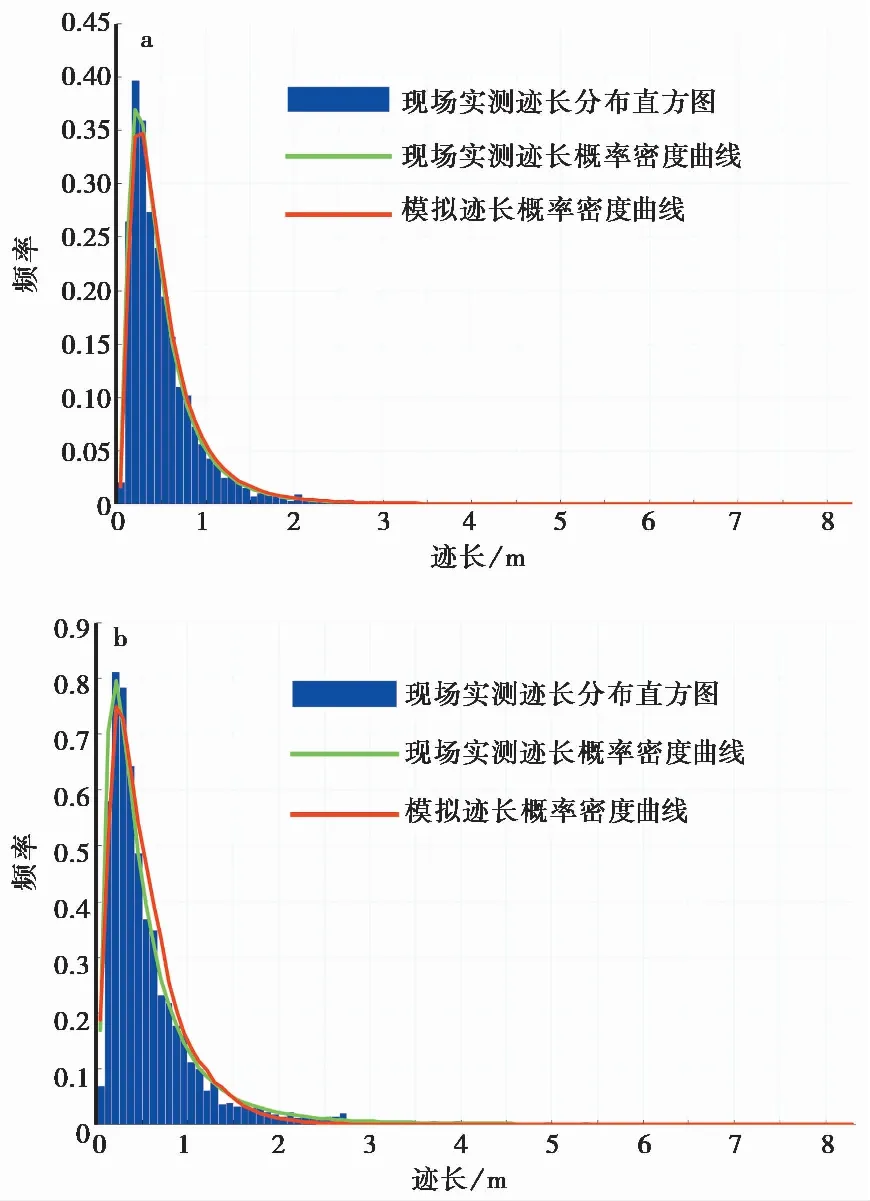
图 9 模拟与实测迹长分布直方图及概率密度曲线Fig. 9 Histograms and probability density curves of the distribution of modeled and collected trace lengthsa. 后缘破裂段; b. 左边界破裂段
5 结 论
本文以汶川县绵虒镇大溪沟沟口的两处斜坡为研究对象,利用三维激光扫描仪、无人机与数字近景摄影测量建立了斜坡坡面及其发育的结构面的非接触式采集方案。基于以上采集数据,建立了高陡斜坡大窗口坡面的三维裂隙网络模拟方法。通过以上研究,得到了如下结论与认识:
较传统结构面人工测量方法,非接触采集技术具有明显的优点。一方面可从宏观尺度上建立结构面的出露规律,方便建立结构面发育特征的定性认识。不管在裂隙网络模拟还是在斜坡力学分析计算上均具有指示意义。另一方面,非接触式采集可得到大范围(窗口)出露的随机构造结构面系统,可充分反映结构面的几何特征,缩小由于结构面特征认识不清与结构面发育不确定性造成的误差。
三维裂隙网络技术是建立随机构造结构面三维展示状态的唯一技术方案。大窗口三维裂隙网络模拟方法是针对于高陡斜坡坡面采集数据的专属技术。这种技术步骤简单,避免了繁琐几何参数推导过程中造成的累积误差,具有更高的可靠性,是未来高陡斜坡“岩体结构控制论”实施中的可推荐方法。
高陡斜坡坡面结构非接触式采集与大窗口三维裂隙网络模拟方法尚有不足之处。例如,坡面上常有植被覆盖。区域性产出的植被对结构面有一定的遮盖作用,一定程度上减小了二维结构面的解析力度与裂隙网络的三维密度。另外,传统与本文裂隙网络模拟技术均视采集窗口为平面; 但实际上高陡斜坡坡面是曲折的,这也就使问题更加复杂化。而且,由于坡表块体的大量掉落,结构面常被一分为若干个独立的子结构面,与坡表近平行的裂隙也极容易暴露,影响了三维裂隙网络模拟的直径与密度。以上这些问题均是未来在高陡斜坡坡面结构非接触采集与三维裂隙网络模拟中需大力研究的。

