带信息干预随机SIRS 模型流行病的持久性及平稳分布

张园园， 亢 婷

（宁夏大学 新华学院，宁夏 银川750021）

当流行病在一个地区开始蔓延时，相关部门通常会通过宣传报道来使人们意识到流行病的存在，人们获知流行病爆发的消息之后会改变自己的行为来降低感染疾病的可能性. 2013 年，Manfredi等［1］研究了人们的行为改变对流行病传播过程的影响.2017 年，Kumar 等［2］将“易感人群行为反应项”引入到舱室模型中，于是得到了如下的具有信息干预的SIRS流行病模型：

其中，S、I、R 和Z 分别表示易感人群、感染人群、康复人群和人群中信息的密度.模型中的参数均为非负常数，Λ表示易感者的常数补充率，β 表示接触率，μ表示自然死亡率，μ1表示人们对信息的反应强度，m 表示由于信息干预使得人们行为的改变率，γ表示感染人群的康复率，ε 表示病死率，δ 表示恢复者免疫丧失率，a表示信息的增长率，b 表示饱和常数，a0表示信息的自然消失率［2］.由于资源、经济水平和不可避免的自然因素的存在，人们对信息干预的反应不会达到100%，所以信息干预项取为μ1mZ（t）S（t）.

在许多传染病模型中，传染病发生率都取为双线性的，即βSI，表示每一次接触中被感染的概率相同.然而有研究表明，非线性的发生率比双线性的更加合理［3-4］.在实际情况中，当感染者人数较多时，发生率会由于对易感者采取保护措施或对感染者进行隔离而降低，而双线性的感染率不能刻画出这种变化，所以应当在模型中引入非线性的发生率.受文献［3］启发，在本文中使用饱和发生率βSI／（1+αI）.

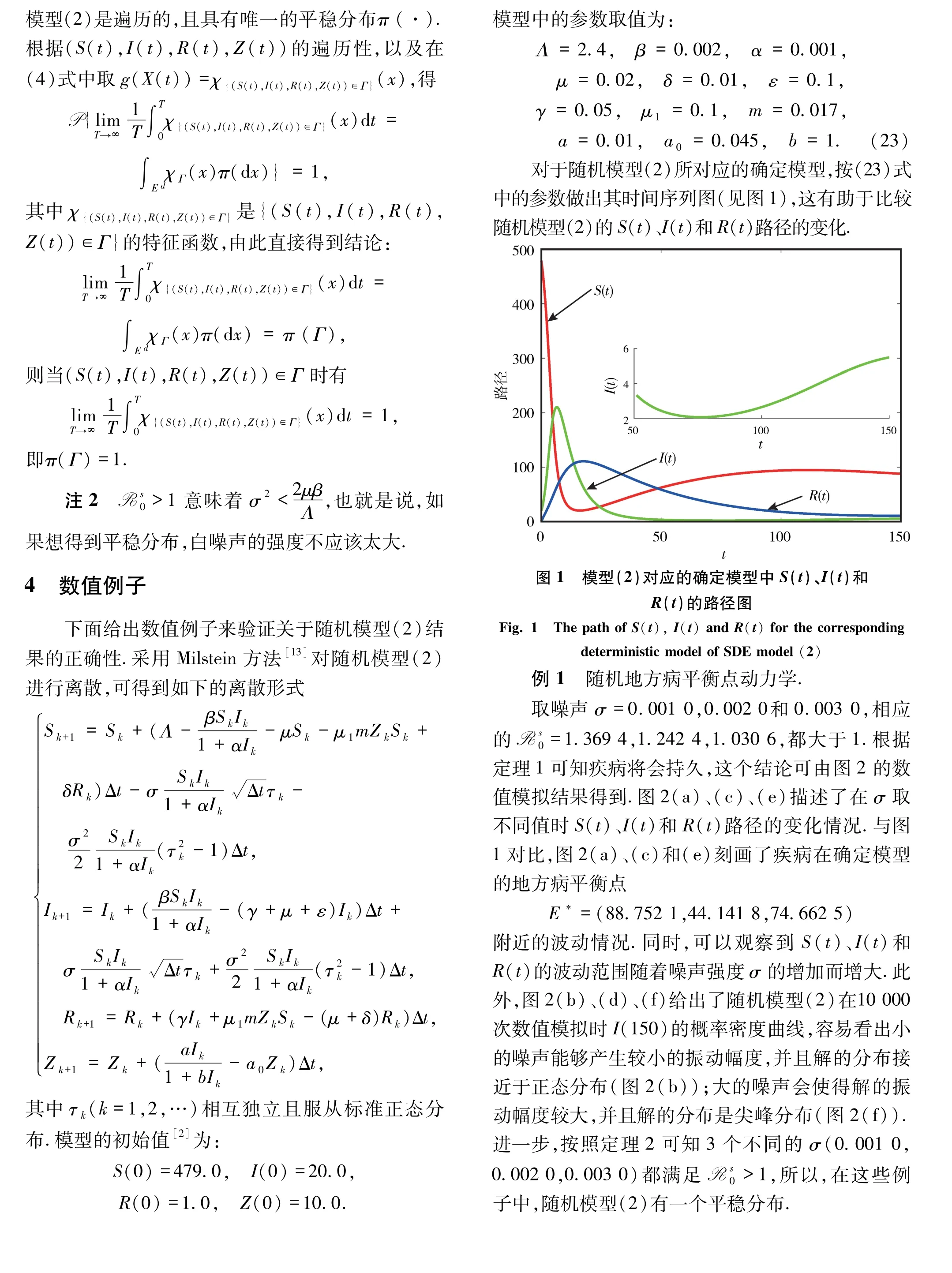
图2 左列表示随机模型（2）中S（t）、I（t）和R（t）在不同噪声强度下的路径，右列表示当σ取不同值时I（150）的概率密度函数的直方图Fig. 2 The left column shows the path of S（t），I（t）and R（t）for SDE model（2）under different noise intensities，the right column displays the histogram of the probability density function of I（150）with different values of σ

5 结论

流行病的爆发给人类的健康和国家的经济产生了严重的影响.本文提出了一个具有信息干预和饱和发生率的随机SIRS 模型，研究了疾病的持久性和随机模型解平稳分布的存在性.最后通过数值例子验证了理论结果.

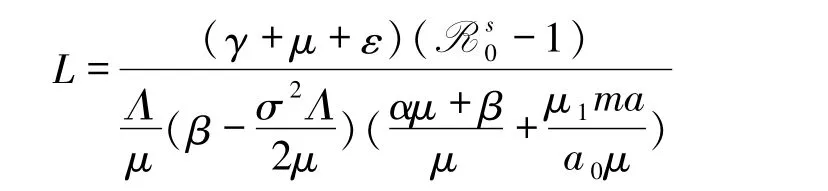
（定理1 中定义的一个常数）的表达式中可以看出I（t）的下界会随着μ1的增大而减小，所以信息干预可能会抑制流行病的爆发.

致谢 宁夏大学自然科学基金（ZR16013）给予了本文资助，谨致谢意.