对“简捷求解一类匀强电场典型问题的解析式”再探讨

郭 威

(南平第九中学，福建 南平 353001)

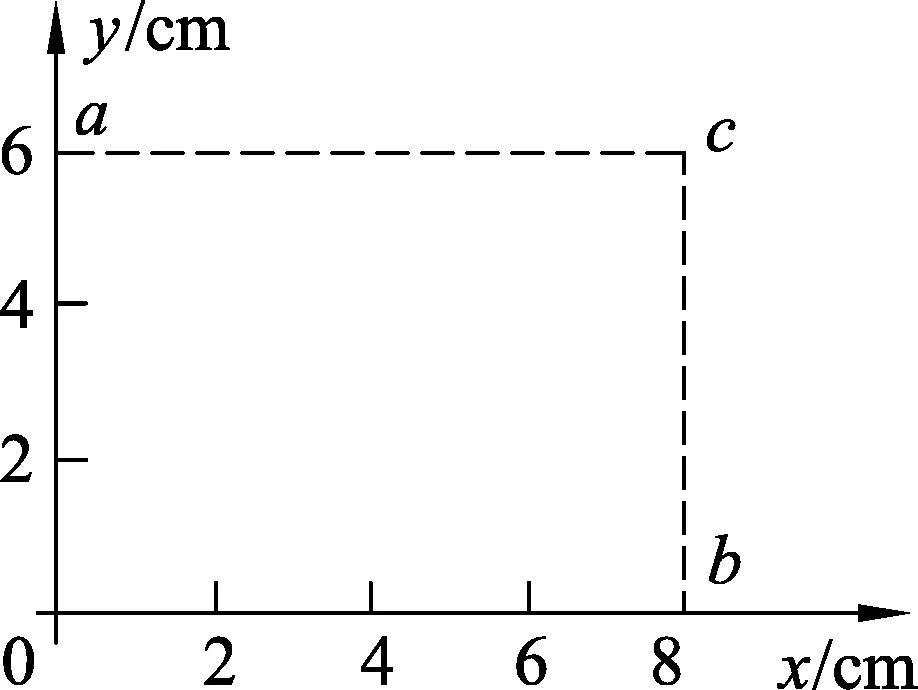
图1

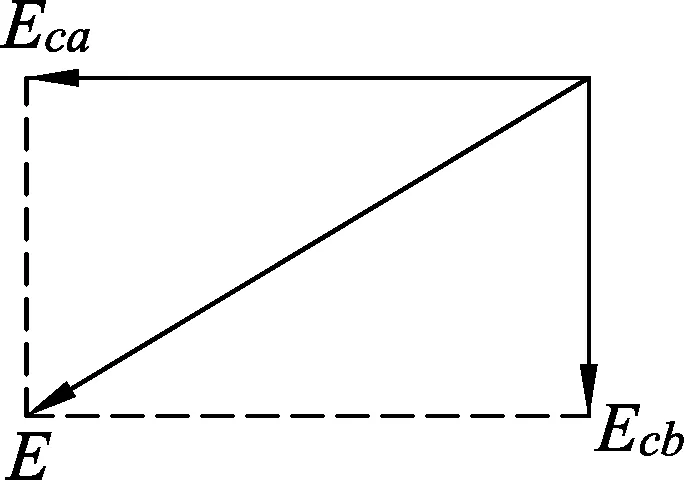
图2

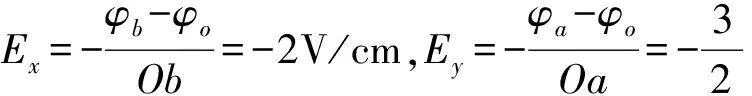
1 提出问题

该文中开头阐述的“高中物理教学中常见这样一类匀强电场的典型问题：假设匀强电场的电场线与某平面共面，已知该平面上某几点的电势数值，要求解场强的大小和方向”是一个普通性的问题，而所举的实例“2017年全国高考课标Ⅲ卷的第21题”的两个分场强是相互垂直的，如果这两个分场强不垂直，这种简捷求解一类匀强电场典型问题的解析式还成立吗？

2 研讨论证

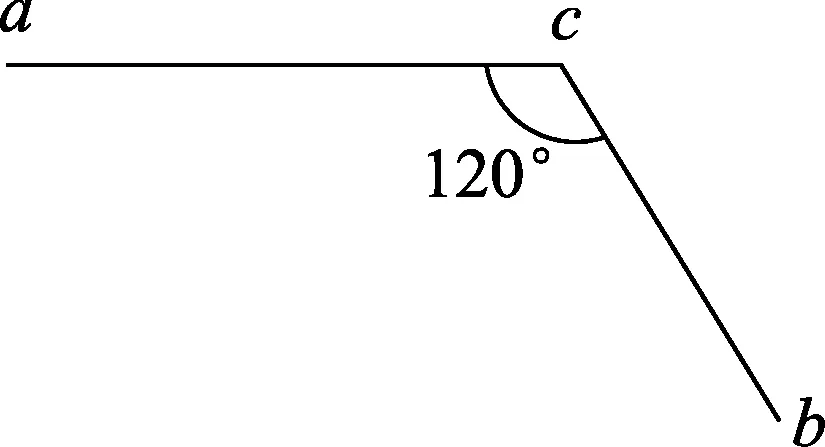
图3

针对这类匀强电场的电场强度，我们把2017年全国高考课标Ⅲ卷的第21题进行情景改编：一匀强电场的方向平行于xOy平面，平面内a、b、c3点的电势分别为10 V、17 V、26 V，ac=8 cm，bc=6 cm，ac与bc的夹角为120°，如图3所示，求电场强度的大小.

先分别求出ca和cb方向的电场分量

2.1 正交分解法

如图4建立直角坐标系，

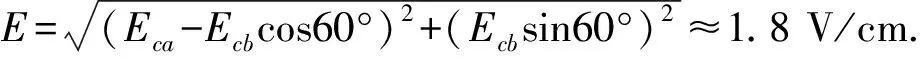
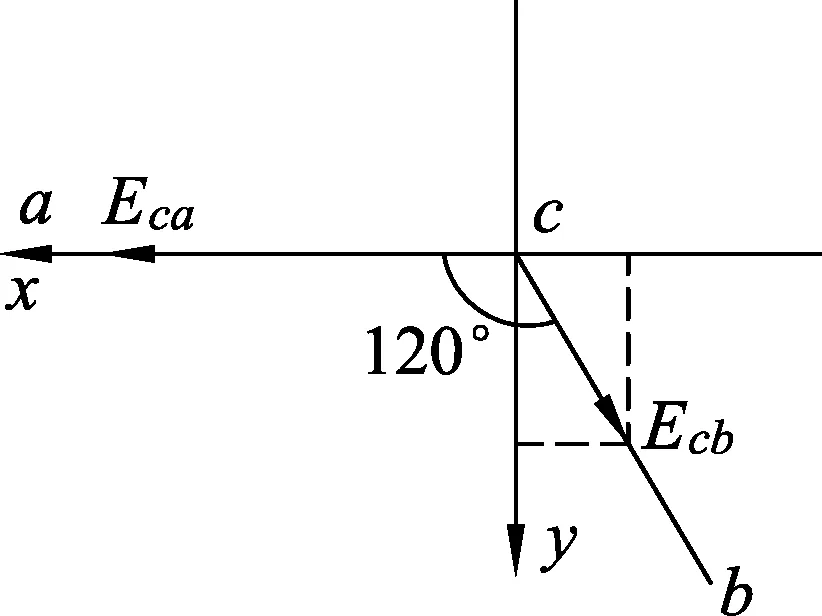
图4

2.2 矢量合成法

如图5用平行四边形法则进行矢量运算，

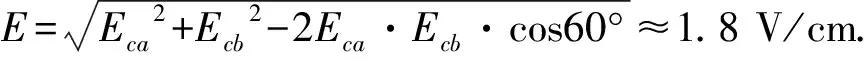
2.3 等电势法(电势等分法)

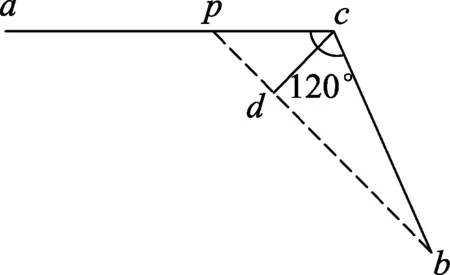
图6

把最高电势点c和最低电势点a连线等分，如图6，由比例关系可知在ac线上与17 V电势相等的p点位于距离c点4.5 cm处，连结pb，pb即为17 V的等势线，过c作pb的垂线，垂足为d，即cd方向为匀强电场方向.根据三角形面积可知

(1)

(2)

(3)

由(1)～(3)得E≈3.51 V/cm.

由上述3种方法求解该电场强度大小可以看出，第一和第二方法结果相同，那是由于第一种与第二种方法其实就是一个原理，所以结果是相同，而第三方法就是《简捷求解一类匀强电场典型问题的解析式》一文中提到的“等电势法”，从数学上看是一种几何法，本题改编后没有特意修改相应数据，步骤的确比较繁琐，等电势点的寻找和几何计算的确很费事，求解过程中的难度也的确相当大，但第三种方法的运算过程虽繁但结果却是本题的最终答案.综上分析可知，《简捷求解一类匀强电场典型问题的解析式》一文遇到两分场强不相互垂直时是不适用的，其解法只是一种特例，即两场强分矢量相互垂直时恰好可行.

3 扩展延伸

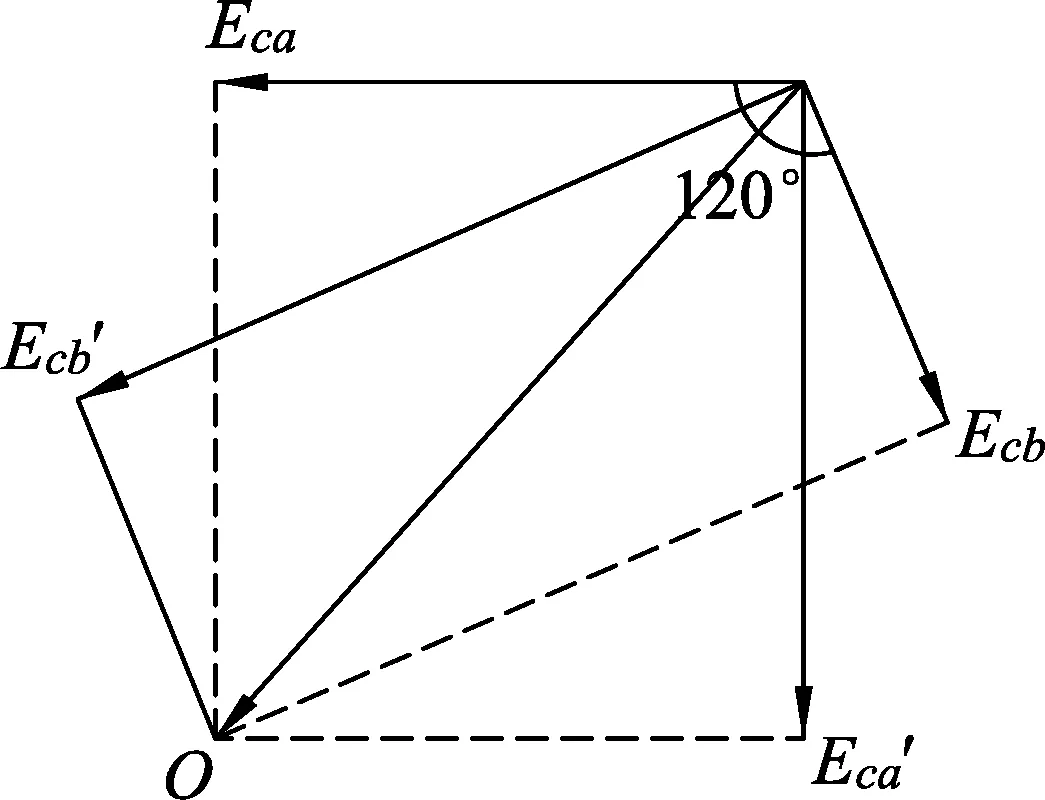
图7

从上面第三种解法求解这一类匀强电场典型问题，即假设匀强电场的电场线与某平面共面，已知该平面上某几点的电势数值，要求解场强的大小和方向，在两场强分矢量相互不垂直的情况下，这两分矢量场强是合场强的分量吗？毋庸置疑，只不过这两个分矢量是合场强两组正交分解中两分矢量中其中的一个分量，直接用这两个分矢量进行合成与分解，明显张冠李戴.根据电磁学中静电场电场强度与电势梯度之间的关系，[2]即电势φ的负梯度等于电场强度E，将E沿匀强电场所在平面的两个直角坐标轴正交分解出两组分矢量，[3]如图7中Eca和Ecb分别为两组分矢量中其中的一个分矢量.为此，我们就可以用下面的方法来找出合场强的大小与方向.

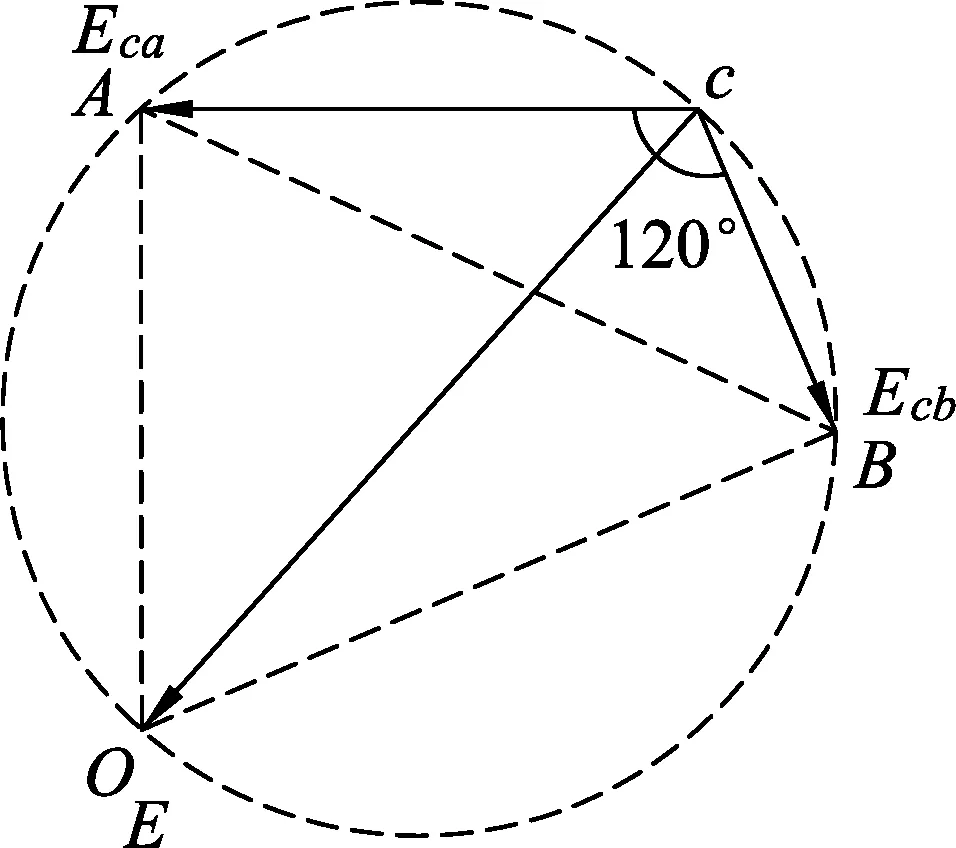
图8

如图8，过Eca的矢量末端A作Eca的垂线，过Ecb的矢量末端B作Ecb的垂线，两垂线的交点为O，cO方向为合场强的方向，根据几何知识可知AOBc4点共圆，

(1)

(2)

根据余弦定理

(3)

根据正弦定理

(4)

(5)

根据圆的几何性质可知

∠cOB=∠cAB,

(6)

由(1)～(6)式得

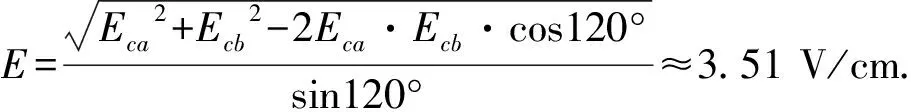
这个结果与“等电势法”结果完全一致.

4 小结