井下震源发生器设计及动力性能仿真

迟少林,冯进,张慢来,刘宇,何臻,李裴晨 (长江大学机械工程学院，湖北 荆州 434023)

丛式井广泛应用于海上平台，其井数多、井距小，在对新油田进行井组布置或者对老油田井组进行加密调整时，要尽量减小井眼发生碰撞的可能性。丛式井井眼一旦发生碰撞，将导致套管破损、钻井液泄露，若被碰撞的井为生产油井，则会直接影响油井产量，甚至停工停产[1,2]。因此，对施工井进行防碰检测，找出可能发生碰撞的井，并采取相应的措施变得尤为重要。通常情况下，震源信号由井下产生，通过井上信号接收装置采集，对信号进行分析，获取井下工具的相对空间位置后，再判断两井位置关系，从而有效避免井眼相碰带来巨额的经济损失。工程上主要通过井眼轨道设计、随钻测量和防碰扫描等技术来减少事故发生，但井眼轨道设计中轨迹拟合方法存在过于理想而偏离实际，随钻测量时因钻头信号不稳定或不足导致信号破译失败，防碰扫描作业中对井距监测难以保证数据准确[3～5]。

从Bailey开发的连续钻头定位系统到美国Western Atlas International公司开发的TOMEXTM系统[6,7]，都是采用钻头破岩产生的震动作为震源，在硬岩钻进方面发挥着不错的作用，但在软岩层产生的震源强度不足;刘刚等[8,9]设计的机械式井下震源能产生合适的震源强度，但由于操作费时繁琐，限制了它的适用范围;邵冬冬等[10]研制的水力脉冲钻井工具，在斜井、大位移井等条件下能产生足够的能量，但增加了井下施工的复杂性;李博[11]利用Matlab数值仿真软件对YZX液动冲击器性能仿真优化，得出流量或冲锤质量增加使得冲击功、冲击功率增加，但冲锤自由行程增加使得冲击频率、能量利用率降低;叶晓平等[12]通过Matlab获取双作用液动冲击器的冲击频率等性能输出结果和实际工况相仿;Tao Wu等[13]利用Ansys对潜孔锤冲击应力分析，认为用滑动轴承来优化锤的结构，新结构的疲劳寿命问题可得到改善。鉴于此，笔者设计一种能产生强冲击的机械式井下震源发生器，并基于流体力学理论，以冲锤为研究对象，建立了井下震源发生器的动力学模型，通过Matlab Gui进行数值模拟程序编制，得出井下震源发生器输出性能变化规律，旨在为设计参数选择提供理论依据。

1 井下震源发生器设计

1.1 结构与工作原理

井下震源发生器结构示意图如图1所示，主要由活塞、弹簧、固定套筒、冲击锤、止推套筒、铁砧和延时装置等组成。止推套筒、铁砧和下接头是螺纹连接，而铁砧与下接头通过花键配合来实现轴向运动。

其基本工作原理是通过液压装置蓄能，弹簧力驱使冲锤冲击铁砧来产生较大震击力。正常钻进状态时，井下震源发生器不会产生震击作用，在钻压作用下，外筒和下接头处于贴合状态，只是作为钻具的一部分传递扭矩和钻压，钻井液推动活塞并带动冲锤向上运动压缩弹簧;当弹簧压缩蓄能，而冲击锤和活塞组合处于钢球卡点处(见图2)时，钢球部分伸出卡住冲击锤的弧形下端。为防止即拉即震或误震，设计出液压延时装置，当微提钻杆，延时装置工作。待延时装置结束延时后，止推套筒也相应下行一小段距离，钢球在弹簧力的作用下退缩到外筒体和固定套筒之间的腔体中，即卡点消失。弹簧能量释放迫使冲击锤和活塞组合迅速下行冲击铁砧(见图3)，实现一次有效震击。

1.2 设计特点

结构简单、易损件少且可更换。活塞系统运动形成液压腔，在正常钻进时，便可以实现弹簧蓄能，避免繁琐操作;停止钻进时，钢球受到止推套筒的约束，在固定套筒的中凸出部分球体，形成卡点，避免冲击锤冲击铁砧。液压延时装置是通过单向阀使钻井液进入液压腔，再通过细长缝压出，时长根据需要可以调节，避免即拉即震或误震。

2 井下震源发生器流体动力分析

2.1 井下震源发生器流体动力学理论基础

在研究井下震源发生器冲锤动力时，需要以流体连续性方程和能量守恒为基础来进行理论分析，同时要考虑压力损失、摩擦阻力等影响因素。

1)连续性方程。连续性方程是流体力学中的一个基本方程，它是质量守恒定律在流体力中的具体表现。对于不可压缩流体，其密度ρ为定值时，其表达式为：

Q=v1A1=v2A2

(1)

式中：Q为流量，m3/s;A1、A2为不同过流面横截面积,m2;v1、v2为不同过流面的平均流速,m/s。

2)伯努利方程。伯努利方程是流体运动时能量守恒和转化规律的具体表达，是流体力学中最重要的方程之一。其表达式为：

(2)

式中：H1、H2为不同过流面的高度,m;p1、p2为不同过流面的压强,Pa;h1为水头损失,m;γ为流体重度,N/m3;g为重力加速度，m/s2。

3)水垫阻力。当冲锤高速下行时，冲锤流道腔内流体并不能及时从排流面积较小的节流孔流出，腔内流体会对高速运动的冲锤产生较大的水垫阻力。水垫的巨大缓冲阻力对冲锤的运动速度会产生比较大的影响。水垫阻力的计算公式[12]为：

(3)

式中：pd为节流环产生的水垫阻力，Pa;Aj为节流环面积,m2;Ac2为冲锤下端面面积,m2;vc为冲锤运动速度,m/s;ζj为节流环处的局部损失数，1。

4)压力损失。流体在腔体内流动时会随着过水断面变化而产生不同的能量损耗。压力损失一般包括沿程水头损失和局部水头损失。

沿程水头损失是均匀流体在过水断面的面积和形状不变的流道内克服沿程摩擦阻力造成的，一般可用达西公式计算：

(4)

式中：hf为沿程水头损失，m;λ为沿程水头损失系数，1;d为管道内径，m;l为腔体流道长度，m;v为平均流速，m/s。

局部水头损失是指由于管道过水断面变化、或流体方向改变、或阀门等附属装置的作用，流体受到扰动后在管路局部范围内产生的能量损失，其计算公式为：

(5)

震源发生器冲锤流道是突然收缩的类型，参考流体力学及输配管网[14]可取：

(6)

式中：hj为局部水头损失，m;ζ为局部水头损失系数,1;v为产生局部损失后的缓变流断面的平均流速，m/s。

5)机械摩擦力Ff。冲锤和冲锤流道之间的摩擦力主要为滑动摩擦力，与密封件的工作压力、压缩量、材料硬度、接触面积、表面粗糙度、运动速度和温度等因素关系较大。其经验估算公式[15]为：

Ff=μπdhp

(7)

式中：μ为接触面摩擦系数,1;h为冲锤有效宽度,m;p为冲锤的工作压力,Pa。

6)冲锤浮力Fb。计算公式为：

Fb=ρgV

(8)

式中：ρ为钻井液密度,kg/m3;V为冲锤体积,m3。

2.2 冲锤动力学模型

根据井下震源发生器工作原理，基于流体动力学理论基础，以震源发生器垂直状态建立动力学模型，利用Matlab Gui进行数值模拟程序编制，冲锤作为震源发生器核心动力部件，主要研究其下行冲击阶段动力性能。

1)受力情况分析。如图4,冲锤受力因素主要有重力G、冲锤下端面压力p1、冲锤上端面弹簧力F、水力阻力Fs：

G=mcg

(9)

p1=p2+pd

(10)

(11)

(12)

式中：mc为冲锤组合质量,kg;p2为背压,MPa;k为弹簧刚度系数,N/mm;x0为冲锤总行程,m;x为冲锤任意时刻的位移量,m;Cs为流体阻力系数,1。

2)冲锤运动微分方程。加速度、速度、位移微分方程分别如下:

(13)

(14)

(15)

式中：v0为初始速度,m/s。

3 冲锤动力性能仿真程序开发

利用有限差分原理，将冲锤的运动周期分割为大量的时间微段，对冲锤在下行阶段的动力学方程迭代计算，求得冲锤在微段内的加速度、速度和位移，再根据这些参数反求水垫阻力、水力阻力等，并将这些参数作为下一时间微段的起始状态参数，如此循环计算，直至计算出最终结果。以冲锤速度方向判断冲锤运动能否冲击铁砧，以冲锤流道长度来限制冲锤的位移，仿真软件的程序流程如图5所示。

利用Matlab强大的计算能力和绘图能力，以Matlab Gui为平台进行数值模拟程序的编制[16,17]。程序中参数输入界面如图6所示，设置了基本的结构参数和水力参数的输入项，如流量、背压、冲锤结构等，通过对这些参数的不同设计组合，并根据设计目标进行参数优化，研究井下震源发生器动力性能输出规律(见图7、图8、图9)。

从图8 和图9可以看出，冲锤速度曲线呈先增后减的趋势变化，即存在最优值。因此，以冲锤速度为优化目标，通过对冲锤结构参数和水力参数的调整组合，就可以得到井下震源发生器的最佳输出性能。

4 弹簧刚度对井下震源发生器输出性能的影响

弹簧是井下震源发生器的主动力蓄能装置，冲锤冲击功等输出性能主要由弹簧势能决定，有必要对不同弹簧刚度对冲锤的动力性能影响进行研究。以冲锤最佳输出性能，即最大冲击功、最大冲击效率等为优化目标，进行井下震源发生器的动力性能优化并改进。冲锤的单次最大冲击功W和对应的冲击效率η计算公式如下：

(16)

(17)

式中：vmax为最大速度,m/s;F为弹簧力,N;x为任意时刻位移,m。

冲锤欲获得最大输出性能，则应该在弹簧形变范围内运动，故以弹簧实际行程为运动行程。弹簧实际行程如表1所示。

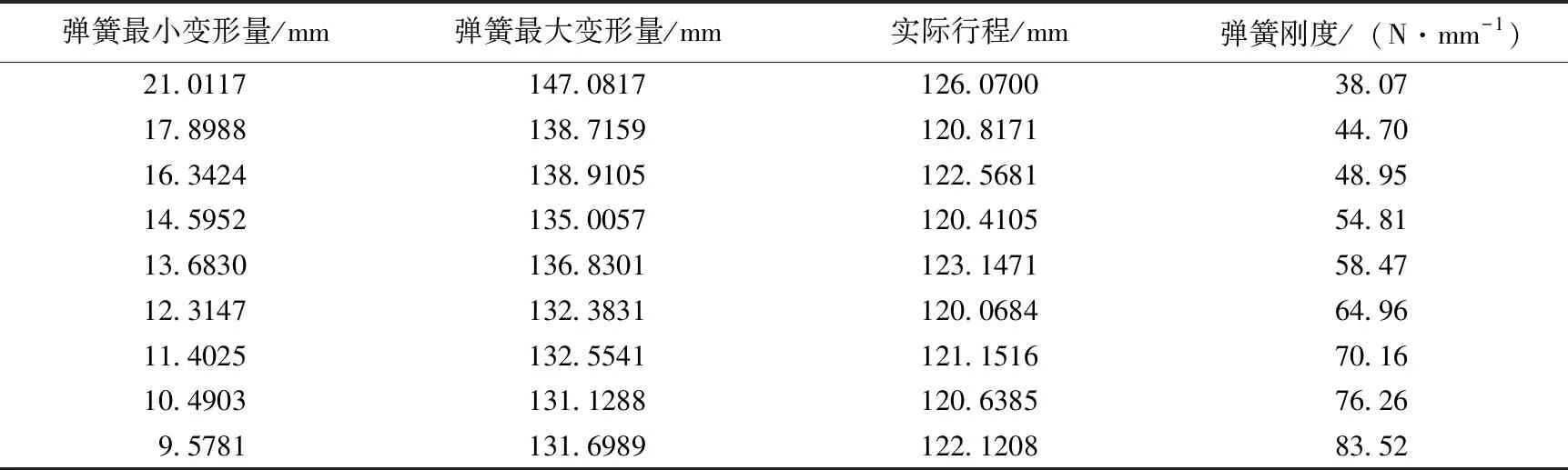
表1 弹簧相关参数表

当钻井液密度分别为1200、1100kg/m3时，可以求出不同弹簧刚度时冲锤的输出性能值。这里以弹簧刚度为48.95N/mm时为例，计算冲锤的各项输出性能值，即冲锤的速度、位移、冲击功、冲击效率，通过Origin绘图软件对冲锤的输出性能数据处理，得出规律曲线如图10所示。从图10可以看出，在冲锤运动行程内，随着时间的变化，冲锤的速度变化趋势是先增后减，这是由于弹簧力逐渐减小，而流体阻力相对增加，导致冲锤加速度逐渐变小的缘故;冲锤位移符合匀加速运动规律，冲锤冲击功变化趋势与冲锤速度变化趋势相似，这是由于冲锤冲击功与速度的平方呈正相关的缘故;冲锤冲击效率呈递减趋势，这是由于弹簧的弹性势能和冲锤的重力势能不只是转化为冲锤的动能还转化为其他形式的能量，导致冲锤的动能增加量相对势能减少量降低的缘故，而斜率绝对值变化先增加后减小，是由于阻力在冲锤运动的前期阻碍能力逐渐增加之后趋于稳定的缘故，而冲锤冲击效率后期递减缓慢验证了这一点。

冲锤在密度分别为1100kg/m3和1200kg/m3的钻井液中工作时各输出性能值的变化规律相似;钻井液密度较低时，冲锤的输出性能比密度高时的更好，即最大速度增加2.88%，最大冲击功提高5.85%，最大速度对应的冲击效率提高4.58%，但达到最大速度所对应的位移相应增加1.73%，而冲锤总行程123mm，达到最大速度时实际行程不足70mm，故增加的位移可忽略影响。取不同弹簧刚度，改变水力参数，求得冲锤各项输出性能，如图11所示。

从图11可以看出，随着冲锤弹簧刚度的增加，冲锤的最大速度呈现递增趋势，而冲锤位移则随着冲锤弹簧刚度的增加呈下降趋势，弹簧刚度越大，达到最大速度的位移越短;冲锤的最大冲击功和冲击效率均呈递增趋势。当弹簧刚度为58.47N/mm时，冲锤最大速度、最大冲击功的增量较为明显，而冲击效率降低，这是由于冲锤运动行程加长，阻力做负功，冲锤的动能增加量相对势能减少量降低的缘故;冲锤的位移较大是和弹簧的选型有关;弹簧刚度受到弹簧设计参数约束，弹簧刚度不能一直增大，一方面井下震源发生器的内径是受限制的，则只能尽量选择较大弹簧刚度的弹簧;另一方面，当弹簧刚度大于76.3kN/mm时，冲锤冲击效率下降且冲锤位移增加，故弹簧刚度为76.3kN/mm时，冲锤的输出性能可达到最佳;能产生的最大冲击功为264.14J;所对应的冲击效率为50.41%;最大冲击速度为2.97m/s;所对应的位移为64.5mm。

当冲锤撞击到铁砧时，将产生非常强劲的冲击力，撞击简化为弹性碰撞，则冲锤以速度v撞击铁砧后反弹，求铁砧所受到的最大冲击力问题。由冲量定理可知：

FdΔt=2mv

(18)

式中：Fd为冲击力，kN; Δt为冲击时间，s。

根据已有的试验数据[8,9]，机械式震源发生器产生的震击力达到51.1kN,能满足防碰监控的需求。井下震源发生器的最大震击力为71.28kN，满足丛式井防碰监控的需求。

5 结论

对井下震源发生器进行结构设计、流体动力分析，并通过Matlab Gui进行冲锤输出性能数值模拟程序编制，最后分析在不同密度钻井液情况下弹簧刚度对冲锤输出性能的影响，得到如下结论：

1)设计的井下震源发生器操作简单，可靠性高。利用钻井液对弹簧的间接作用力实现可提前蓄能，通过接卡延时后，能对铁砧进行有效地冲击。

2) 建立冲锤的动力学模型，通过数值模拟程序编制，能直观地看出井下震源发生器输出性能图;改变设计参数的组合方式，能得出震源发生器输出性能变化规律。

3) 弹簧刚度越大，冲锤最大速度、最大冲击功和冲击效率越大，而冲锤位移越小，但弹簧刚度受设计参数约束，只能尽可能取较大值，这为井下震源发生器的设计参数选择提供了理论依据;钻井液密度较低时，井下震源发生器的输出性能较好,且满足丛式井防碰监控的需求。