粮油食品中微生物和真菌毒素污染预测模型研究进展

裴鹏钢 熊 科 叶 宏 王小艺 赵峙尧 柳佳芸 邓 蕾

(北京工商大学北京市食品添加剂工程技术研究中心1,北京 100048)(北京工商大学北京市风味化学重点实验室2,北京 100048)(北京工商大学北京市质量与安全重点实验室3,北京 100048)(北京工商大学北京食品营养与人类健康高精尖创新中心4，北京 100048)

1 粮油食品预测微生物学

稻谷、小麦、大豆等大宗粮油食品是我国粮油食品加工的主要种类。而在这些粮油食品生产加工过程中，供应链环节链条长，各环节污染物种类多、来源复杂，致使粮油食品从原料种植到储藏运输等不同阶段均易遭受微生物尤以霉菌及其产生毒素污染。迄今为止在粮油食品中已发现300多种真菌毒素，主要为黄曲霉毒素、脱氧雪腐镰刀菌烯醇、赭曲霉毒素、展青霉素、单端孢霉烯族毒素、玉米赤霉烯酮、伏马毒素等[1]。不同类型粮油食品中的产毒霉菌并非完全相同，即使同一种粮油食品中加工或储藏不同阶段或不同的环境条件下的有害菌也不尽相同[2]。

以小麦供应链主要环节为例，在其种植期间容易遭受赤霉病、叶锈病、纹枯病等真菌病害的侵染，造成小麦减产，并且产生的真菌毒素在小麦中形成积累；其次，在小麦原粮仓储阶段由于粮堆各部分贮藏温度不同，再加上外界条件变化导致湿度变化使得小麦也极易遭受镰刀菌、青霉菌、交联孢菌及其次级代谢产物如脱氧雪腐镰刀菌烯醇(DON)、玉米赤霉烯酮(ZEN)、黄曲霉毒素(AFB1)的污染[3]。同时小麦制粉阶段润麦环节两次润麦处理，导致粮堆水分含量增加，润麦仓仓储环节为微生物的生长繁殖创造良好的条件。同时小麦粉在贮藏阶段卫生状况也会影响小麦粉中的微生物数量；在产品运输环节，环境的差异同样也会导致小麦粉霉菌等腐败菌的数量增加。因此小麦供应链中存在真菌毒素污染物影响产品安全的较大风险，而对于供应链的污染物难以逐一进行分析研究，只能聚焦于关键阶段对其进行控制分析。

预测食品微生物学(Predictive Food Microbiology)是结合微生物学、数学、统计学和计算机等学科，采用数学的方法描述微生物数量变化和外部环境因素之间的关系，并对微生物的生长动态情况做出预测。因此为了确保食品安全性，科学家们通过引入预测食品微生物学理论对食品中的微生物进行量化和行为预测。通过计算机软件进行病原菌和腐败菌生长及其产生的污染物在特定条件下的概率模型等的拟合[4]，快速判断食品内主要病原菌和腐败菌生长或残存的动态变化以及有害物含量的高低，从而依据标准对特定阶段食品的安全性作出快速评价。表1为近年来国内外对食品如玉米、水稻、麦芽等食品中的霉菌生长动力学模拟研究情况。

因此，针对粮油食品供应链污染物特点，采用预测微生物学模型的方式对其供应链中关键环节的毒素污染产生菌构建动力学模型以及通过不同条件下产毒概率模型，探究关键环节毒素变化及降解迁移规律，从而实现对粮油产品关键环节品质的安全评估与预测。通过模型的反馈来优化粮油产品贮藏及加工的方法和手段，实现“绿色储粮”和“生态储粮”，为确保粮油食品安全提供重要的理论依据。这也为未来开展粮油食品供应链真菌毒素污染的安全风险评估以及对其供应链中真菌毒素危害物预警追溯等奠定模型基础，满足粮油食品供应链安全与社会可持续性发展的需求。

表1 近年国内外关于食品霉菌生长动力学模拟情况

2 粮油食品中真菌毒素污染情况

国内目前大宗粮油食品真菌毒素污染超标问题严重，对消费者的身体健康带来极大的安全隐患。稻谷、小麦、大豆、花生等大宗粮油食品中均发现真菌毒素不同程度污染的情况。

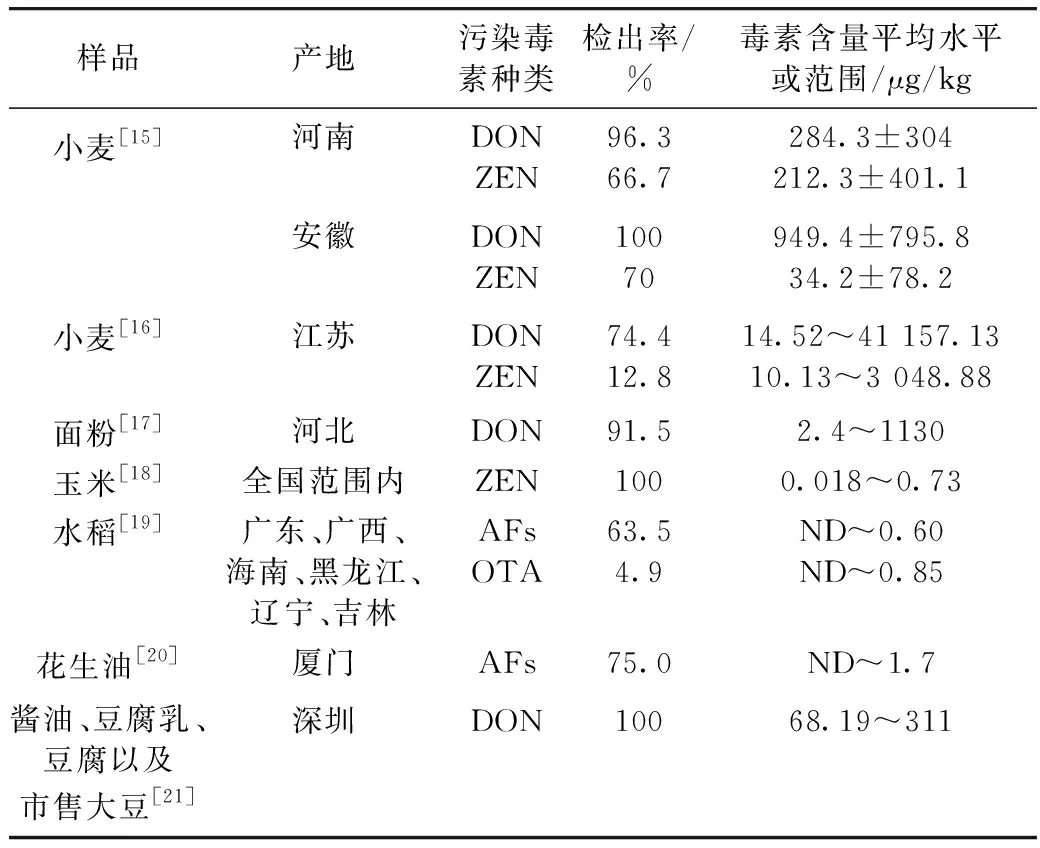
表2 近年国内粮油食品真菌毒素污染调查

注：ND指的是未检出相应毒素。

3 微生物预测模型

微生物预测模型最早应用于食品贮藏阶段细菌生长模型，同时期微生物学预测模型对霉菌并未有同等程度的关注研究，这与霉菌生长的量化复杂性有关。细菌裂变繁殖通常发生在食物表面或者液体基质而霉菌菌丝则可穿透食品的物理三维空间，所以对其定量分析更加复杂。并且产生有用且可靠的模型的先决条件必须是包含大量相关数据的数据库，这对于研究真菌毒素来说无疑是巨大的挑战。一般来说，微生物模型分为三类。初级模型是用来描述微生物在一定生长条件下其数量随时间的变化关系，如孢子的萌发、菌株生长、菌体的失活等[22]。Zwietering等[23]比较了几种S形函数(logistic，Gompertz，Richards，Schnute和Stannard)来描述细菌生长曲线，通过t检验、F检验发现Gompertz曲线10 ℃条件下植物乳杆菌数量随时间变化的拟合度最高(见图1)；而二级模型在一级模型的基础上增加了环境因素，如：温度、水分含量、pH等因素，表征环境条件的改变如何影响菌株的萌发和生长。图2为评估水分活度为变量菌株径向生长速率二级模型拟合图；三级模型是一种软件化模型，软件包括了1个或者多个一级模型和二级模型，作为完整的预测工具为用户提供服务[24]。

图1 10 ℃生长的植物乳杆菌相对种群大小随时间变化Gompertz曲线

图2 22 ℃条件下模拟UG AF06菌株在全黑胡椒粒不同水分活度下菌株径向最大生长率实测模型拟合图

概率模型用于描述某一特定时间段某些事件发生的可能性，例如，特定条件下菌体是否生长、是否产生毒素。通过概率模型可以对某种食品基质在特定时间点的安全性做出快速评价[25]。

3.1 微生物生长初级模型

常用的一级模型主要有Logistic方程[25]、Gompertz模型[25]、Baranyi & Roberts模型[26]、Boltzmann模型[27]、致死模型[28]。

3.1.1 Logistic方程：

3.1.2 Gompertz模型：

y=a·exp[-exp(b-cx)]

式中两个模型中的参数只是数学意义上的参数(a,b,c，…)，并不具有生物学意义，不能直接用于微生物生长曲线的拟合。需要对其中的参数进行修改，使用具有生物学意义的参数如(λ，μm，A)来代替纯数学参数(a,b,c，…)。

修正后的Logistic模型：

修正后的Gompertz模型：

式中：μm为最大比生长速率，定义为生长曲线拐点处的斜率；λ为迟滞期时间，滞后期被定义为定义最大特定生长速率的线与时间轴的交点；t为培养时间；A指微生物数量达最大值；N0为初始孢子数；N为t时间后存活的孢子数量。Dantigny等[29]通过实验比较Logistic模型和Gompertz模型，通过比较RMSE值(均方根误差)发现两者拟合优度类似，无法确定哪种模型在特定实验条件下为首选，继而通过评估其他标准如参数估计值的准确性来进一步判断如：评估孢子萌发时间(50%孢子萌发所需时间)时，Logistic模型的精确度更高；而Gompertz模型可以更准确地估计迟滞期时间。

3.1.3 Boltzmann模型

3.1.4 Baranyi & Roberts模型

式中：μm为最大比生长速率(定义为拐点处生长曲线的斜率)(mm/d，μm/h)；λ为迟滞期时间；t为培养时间；A为微生物数量最大值。

Lo′pez等[30]评估微生物生长模型(光密度方法定量)确定包括真菌和细菌在内物种，采用包括Gompertz和Baranyi & Roberts模型在内的各种模型进行拟合，发现Baranyi & Roberts模型拟合度最高；Marin等[31]研究lineal模型、Gompertz模型及Baranyi & Roberts模型对14种常见食物腐败真菌生长一级模型的适用性，采用菌落直径进行生长速率表征发现：当所获数据没有发现渐进趋势时，使用liner模型和Baranyi & Roberts模型可以更好地估计最大生长速率和迟滞期；当观察到生长速率随时间降低时，Baranyi & Roberts模型的拟合度更高。

3.1.5 致死模型

模拟温度高低或致死剂浓度对微生物群体致死处理模型时，使用经典的一级方程对孢子灭活建立模型：

式中：N为孢子数；N0为初始孢子数；N(t)为经过处理后孢子数；ki为致死率/min-1。

现今大多数孢子灭活模型研究采用线性灭活方法，但是目前对于孢子灭活的研究还较少且只有少部分应用于真菌[32]。

3.2 微生物生长二级模型

二级模型主要有Ratkowsky平方根模型[32]、Arrhenius-Davey模型[33]、Rosso cardinal模型[34]、Polynomial模型[35]、Gamma Concept模型[36]。

3.2.1 Ratkowsky平方根模型

该模型最初是为细菌开发的。

式中：μm为最大比生长速率；b2、C2均为假定系数；Tmin2为最低生长温度；Tmax2为最高生长温度。通常该模型仅有温度变量，Tassou等[37]在建立温度和水分活度对合成葡萄汁培养基上希腊酿酒葡萄中2种产生赭曲霉A的炭曲霉菌株模型时，将Ratkowsky平方根模型变量拓展到其他变量因素上如水分活度。

3.2.2 修正的线性Arrhenius-Davey方程

最初用于描述温度对细菌生长的影响，Panagou等[38]模拟温度、pH和水分活度对从绿茶橄榄提取的红曲霉生长速度影响时，将该模型变量因素延伸到pH和水分活度。

lnμmax=C0+C1/T+C2/T2

式中：μ为菌落生长速率；T为开氏温度；C0、C1、C2为3个参数。

3.2.3 Rosso cardinal模型

Rosso等[34]在1993年提出了这个温度模型，使用3个基本温度(Tmin、Tmax、Topt)，和最佳温度下的生长速率μopt。该模型是在经验基础上建立的作为描述数据的工具，模型的优点是所有参数都具有生理学意义，有利于对初始参数的估计。

μR(T,aw)=μopt·τ(T)·ρ(aw)

式中：μR为菌落径向生长速率；μopt菌落直径最大值；Tmin、Tmax、awmin为菌株可以生长的最低和最高温度以及最小水分活度；Topt、awopt为菌落直径达到最大值时对应的温度和水分活度；awmax为1，方便计算无特殊意义。

3.2.4 Gibson模型

Gibson模型是第一个专门为霉菌开发的模型，Gibson等[35]发现真菌生长速率的对数与(1-aw)的平方根呈抛物线关系，所以将多项式模型应用于黄曲霉的生长。

式中：μ为菌落生长速率；a0、a1、a2为3个需要估计的参数。

Tassou等[39]研究环境温度(25 ℃)和选定温度(45、55 ℃)下的高静水压力对火腿中金黄色葡萄球菌的灭活动力学建模，在Gibson模型中增加温度变量。

式中：a0、a1、a2、a3、a4、a5为3个需要估计的参数。

3.2.5 Gamma Concept模型

Gamma Concept模型由Zwietering等[36]提出，认为影响微生物生长速率的各种因素可以通过单独效应的乘积来组合。使用这种方法的优点是，对于确定影响生长速率每个变量，可以通过分离各种变量的影响来计算相对效应。这个模型有一般形式：

其中给定变量的相对影响可以通过该变量的gamma因子来描述：

3.3 概率模型

当实验目标是观察在特定条件下微生物是否生长时，即可采用概率模型来进行拟合。概率模型在很多情况下可确保食物不受微生物污染至关重要，尤其适用于涉及病原微生物或者产毒微生物污染的情况。概率模型允许在各种条件下预测特定事件(例如微生物的生长和毒素的产生)是否可能发生，其中增长概率模型是根据特定时间点在整个实验设计中“增长/无增长”响应的比例构建的[40]。

Logistic回归模型是判断菌株增长/无增长边界的有用工具，将事件发生概率Y与条件变量进行关联。

式中：xi为因子变量(T,aw,pH,…)；bi为要估计的常数。

4 粮油食品中的微生物预测模型的应用

现阶段对于模型的应用大多集中在产品的储藏阶段：真菌的动力学模型、外界条件影响的二级模型、毒素积累模型以及产毒概率模型。目前人工模拟的储藏实验一般通过控制粮油食品储藏环境中的温度和湿度来控制微生物的生长以及毒素的产生。通过人工模拟储藏实验能对实际微生物的生长和产毒的情况进行准确预测，以达到预警的目的。对于产品的加工阶段由于没有合适的可控外界条件，因此目前加工阶段关于模型的研究还较少。

4.1 储藏阶段动力学模型

小麦在储藏中更易滋长霉菌，最容易感染呕吐毒素(DON)和玉米赤霉烯酮(ZEN)等真菌毒素[41]。彭坚等[42]以小麦为基质建立了黄曲霉在小麦贮藏阶段的初级和二级模型，分别利用Gompertz模型、Logistic模型对黄曲霉在小麦中生长曲线进行拟合，通过t检验和F检验发现Gompertz模型拟合效果更好，符合黄曲霉生长规律。利用Ratkowsky方程拟合不同温度下黄曲霉生长二级模型发现先R2相关性比较好, 达到0.99以上。

玉米是我国三大粮油食品品种之一，其在储藏期间极易遭受灰绿曲霉和黄曲霉的污染[43]，短期内可能发生霉腐变质现象。岳晓禹等[44]进行温度对储藏玉米中霉菌生长动力学模型构建，以储藏玉米霉菌为研究对象，在不同储藏温度、不同时间条件下用修正的Gompertz方程拟合腐败霉菌的生长动力学模型，采用修正的线性Arrhenius-Davey方程和二阶多项式方程拟合温度对玉米中霉菌生长的比生长速率和迟滞期的影响，通过模型验证表明修正的线性Arrhenius-Davey方程可以较好地描述、预测不同温度对玉米中霉菌的比生长速率和迟滞期的影响。

房保海等[45]在不同温度和相对湿度条件下对花生中的黄曲霉菌株生长特性进行测定，并采用Boltzmann 和Logistic模型对其生长曲线进行拟合，结果表明在适宜温湿度条件花生黄曲霉生长曲线更适合用Boltzmann 模型拟合。

Yue等[46]在大米干燥过程对大米黄曲霉增长率和迟滞期影响的建模研究中，利用Baranyi & Roberts模型较好地拟合了黄曲霉在大米中的生长曲线，利用线性Arrhenius-Davey模型描述不同水分活度下黄曲霉生长速率和迟滞期，通过模型验证具有较高的R2和较低的MSE值，模型具有良好的拟合度。利用二阶多项式模型来拟合温度和水分活度对生长率和迟滞期的共同作用，通过模型成功预测出该类大米中黄曲霉生长的最适温度，对水稻的贮藏保鲜至关重要。

Mousa等[47]以抛光大米和糙米为基质，通过控制温度和水分活度来对2种不同基质条件黄曲霉径向生长速率和黄曲霉毒素的产生分别进行建模分析。通过Baranyi模型较好地拟合菌落半径随时间变化模型，利用线性Arrhenius-Davey模型和多项式模型拟合温度和aw对黄曲霉生长速率的影响，并通过独立的实验数据对模型加以验证，结果表明线性Arrhenius-Davey模型是抛光大米和糙米上黄曲霉生长速率的最佳预测模型，预测黄曲霉的最适生长温度为30 ℃。

Marin等[48]研究温度、湿度等外界条件对开心果贮藏的影响，人工模拟不同温度、水分活度对开心果中的黄曲霉生长影响进行建模分析。利用Davey模型、Gibson模型、一般多项式模型、多因子cardinal模型和改进的cardinal模型五种方法评价黄曲霉径向生长速率μR对环境的响应值。通过均方根误差(RMSE值)判断发现cardinal模型对黄曲霉的径向生长速率拟合度较高。同时利用改进的cardinal模型(减少观测实验值数量)拟合的同时发现预测值更接近于观测值，但因为存在偏差估计，r2只有0.67而多因素cardinal模型r2为0.78。改进的cardinal模型是基于减少的实验观测点开发的，从而使验证步骤的预测烦琐程度得到改善[49]。

4.2 菌株生长边界模型及毒素积累预测模型

Battey等[50]利用Logistic回归模型预测腐败霉菌生长概率，以0、1进行赋值。0代表无霉菌生长，1代表有霉菌生长。发现pH、可滴定酸度、糖含量、苯甲酸钠和山梨酸钾水平都是影响霉菌随时间存在生长可能性的重要因素。该Logistic回归模型针对14种新条件进行了验证，并预测了8周后霉菌的生长状况，准确度超过96%。产品开发人员可以使用该模型来预测即饮饮料中的霉菌生长状况。

Marín等[51]将概率模型首次应用于霉菌毒素的积累，在不同水分含量和贮存温度条件下预测从开心果中分离出的A.carbonarius菌株的生长和OTA生产边界。在评估水分含量对辣椒中黄曲霉生长的影响利用logistic回归模型对黄曲霉生长边界进行预测，结果表明，将辣椒或者辣椒粉的水分含量保持在30%以下，黄曲霉生长概率低于50%，辣椒含水量低于1%时，黄曲霉不生长。

Lindblad等[52]在温度10～25 ℃，水分活度0.77～0.95 条件下对谷物接种疣孢青霉孢子展开谷物贮藏实验。通过检测青霉菌代谢产物OTA的水平是否超过法定限制5 mg/kg同时根据检测值将疣孢青霉生长观察值定值0或1。即0代表不生长，1代表生长。在不同的温度和水分活度条件下，谷物疣孢青霉菌落达到一定数量时，利用Logistic 回归模型计算超过法定限度的概率，通过模型有效地将谷物霉菌生长与产毒结合起来。

5 问题及应用展望

5.1 存在的问题

粮油食品供应链链条长环节多，危害物种类多，产生机理复杂。霉菌毒素可以在田间以及仓库贮藏期间产生，并且不同的气象条件、种植环境以及农艺技术等都会影响霉菌的生长及其次级代谢产物的产生。由于其危害物产生机理的复杂性，源头控制危害物难度较大，因此宜采用预测模型的方式对关键环节如贮藏阶段、加工环节等进行优化。

而目前对于预测模型研究存在的主要问题是模型数据源不完整，覆盖不全面。以小麦真菌毒素模型构建为例，模型的构建不可能针对于所有的小麦品种，只能针对于特定区域小麦品种进行分析。同时预测模型的可信度和精准度也存在风险。现今大多数微生物模型的拟合都集中在实验室基础上进行仿真模拟，针对相应食品基质或者对应基质培养基来进行，但是经研究发现两者拟合出的数据存在较大差别，后者拟合模型普遍存在可信度低的问题。且实验室基础的模型拟合只能是在有限的条件下，基于所获得的有限数据基础上的拟合，数据的不足是制约模型拟合精准度的最大难题。目前只能通过尽可能多的获取数据来进行模型构建，但大量数据的获取和数据库的构建本身就是难度很大的挑战。

5.2 展望

目前粮油食品中危害物的预测模型还主要是集中在对危害霉菌的生长预测模型研究，霉菌产毒素积累预测模型、产毒概率模型研究还比较少。今后应重点关注毒素预测模型，通过毒素含量及特定条件下的产毒概率直观地反映食品的安全状况。现阶段对粮油食品加工过程中真菌毒素消减规律及加工阶段毒素模型研究还较少。未来需要对加工阶段的某些关键点进行大量模型参数拟合研究，以通过模型对加工阶段的关键参数进行控制改进，尝试进行加工环节的预警溯源分析。同时模型本身的构建基于大量实验数据的获取，这在实验室研究基础上是比较棘手的问题。因此只有通过在粮食食品供应链各环节中大量获取真实有效的数据才能建立起较完整的粮油产业供应链微生物预测模型，这对建立适合我国国情的微生物预报体系具有极其重要的意义。