一类无限维李代数的Centroid

吴祺伟 施晨苗 高寿兰

(1.上海大学 数学系, 上海 200444; 2.上海师范大学 数理学院, 上海 200234;3.湖州师范学院 理学院, 浙江 湖州 313000)

0 引言

本文将研究一类无限维李代数G[5], 它作为复数域上的向量空间, 有一组基}, 并满足如下关系式

张悦等[5]研究了李代数G的结构, 计算了G的二上同调群和Leibniz二上同调群. 本文将研究李代数G的Centroid, 通过计算得到李代数G的Centroid为:Γ(G)=id.这一结果与文献[3]中得到的扩张Schrödinger-Virasoro李代数及其泛中心扩张的Centroid是相同的, 但与文献[4]的结果有所不同. 在文献[4]中, 当,λ=1时, 李代数Lλ,μ的Centroid与李代数G的Centroid不同, 在其余情况下结果相同. 这一结果为今后进一步确定李代数G的Poisson结构奠定基础.

1 李代数G的Centroid

定义1.1[6]设L是一个李代数, 定义L的Centroid为Γ(L):

Γ(L)={χ∈End(L)|χ([x,y])=[x,χ(y)], ∀x,y∈L}.

定理1.1 李代数G的Centroid为: Γ(G)=id.

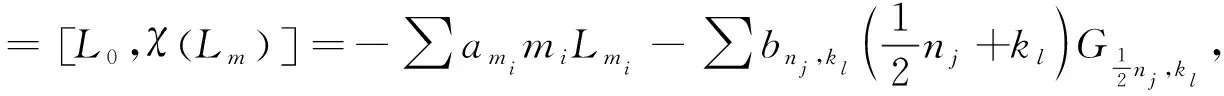
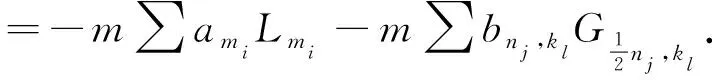
χ(Lm)=amLm+∑b2(m-kl),klGm-kl,kl.

(b)对于等式χ([G0,0,Lm])=[G0, 0,χ(Lm)],

左边=0,

右边=[G0,0,amLm+∑b2(m-kl),klGm-kl,kl]=-∑b2(m-kl),klklGm-kl,kl,

于是, 我们有

klb2(m-kl),kl=0.

以下分两种情形进行讨论.

情形一:b2(m-kl), kl=0. 此时

χ(Lm)=amLm.

对于等式χ([Lm,Ln])=[Lm,χ(Ln)],

左边=(m-n)am+nLm+n,

右边=(m-n)anLm+n,

于是, 我们有

(m-n)an=(m-n)am+n.

(1)

在(1)式中, 取n=1,m≠1,得

a1=am+1,m≠1.

即

a1=am,m≠2.

(2)

在(2)式中, 取m=3,得

a3=a1.

(3)

在(1)式中, 取m=1,n=2,得a3=a2.结合(3)式, 可得

a2=a1.

(4)

结合(2)与(4)式, 我们有

am=a1,∀m∈.

所以

χ(Lm)=a1Lm.

情形二:kl=0. 此时

χ(Lm)=amLm+b2m,0Gm,0.

对于等式χ([Lm,Ln])=[Lm,χ(Ln)],

左边=(m-n)am+nLm+n+(m-n)b2(m+n),0Gm+n,0,

右边=(m-n)anLm+n-nb2n, 0Gm+n, 0,

于是, 我们有

(m-n)an=(m-n)am+n.

(5)

-nb2n, 0=(m-n)b2(m+n),0.

(6)

对于(5)式, 由情形一中的讨论可知

am=a1,∀m∈.

在(6)式中, 取m=n≠0,得

b2n,0=0,n≠0.

(7)

在(7)式中, 取n=-1,得

b-2, 0=0.

(8)

在(6)式中, 取m=1,n=-1得2b0,0=b-2,0.结合(8)式, 可得

b0, 0=0.

(9)

结合(7)与(9)式, 我们有

b2n,0=0,∀n∈.

因此

χ(Lm)=a1Lm.

结合情形一与情形二, 并令a1=k1,可得

χ(Lm)=k1Lm,

这里k1为任意常数.

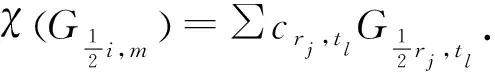
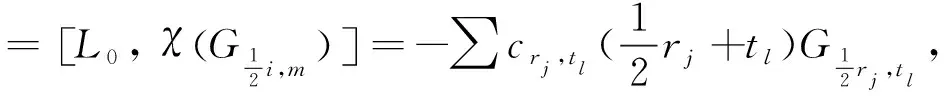
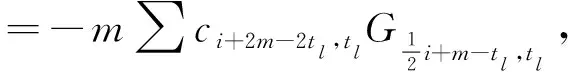
右边

所以tlci+2m-2tl,tl=mci+2m-2tl,tl.于是, 当ci+2m-2tl,tl≠0时,tl=m.因此

于是, 我们有

(m-n)cj, n=(m-n)ci+j, m+n.

(10)

在(10)式中, 取n=1,m≠1,j=1,得ci+1,m+1=c1,1,即

ci, m=c1,1,∀i∈,m≠2.

(11)

在(11)式中, 取m=3,得

ci,3=c1,1,∀i∈.

(12)

在(10)式中, 取m=1,n=2,得ci+j, 3=cj, 2, 即

ci, 3=cl,2,∀i,l∈.

(13)

结合(12)与(13)式, 可得

ci, 2=c1, 1,∀i∈.

(14)

结合(11)与(14)式, 可得

ci,m=c1,1,∀i,m∈.

令c1,1=k2,我们有

这里k2为任意常数.

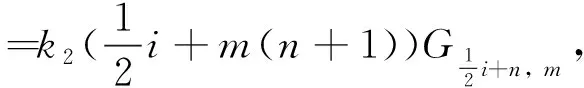
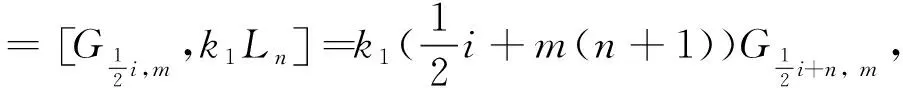
于是, 我们有

(15)

k1=k2.

令k1=k2=k,我们有

χ(Lm)=kLm,

即

χ=kid,k为任意常数.

因此, 李代数G的Centroid为: Γ(G)=id.