埋深对可液化场地地铁车站地震响应的影响

许民泽，崔春义，姚怡亦，王广兵，梁志孟，厉超吉，王启福

1)大连海事大学土木工程系，辽宁大连 116026; 2)大连海事大学安全工程系，辽宁大连 116026

地铁车站由于隐蔽性强、复杂性大、造价高，一旦发生震害破坏，易造成巨大经济损失[1-2]. 地铁车站结构性能极易受到周围土体地震动响应特性的影响，特别是对于可液化场地，场地液化引起的大变形会加大震害程度[3-5]. 可液化场地中地铁车站结构的地震动响应极其复杂，震动过程受到多种因素的影响，其中埋深是比较重要的影响因素. 针对埋深对地铁车站结构地震响应的影响，国内外学者已经取得了诸多研究成果. 刘华北等[6]采用非线性液固两相体动力有限元软件DIANA SWANDYNE-Ⅱ，建立了地铁地下结构在不同埋深条件下的数值计算模型，分析水平地震动作用下地下结构在不同埋深时的上浮效应、加速度响应、水平位移和结构内力. 李长青等[7]建立了不同埋深条件下的日本大开地铁车站数值计算模型，从应力和位移角度分析埋深对车站结构动力响应的影响. 林利民等[8]分析了埋深对地下结构中柱和楼板动力响应的影响规律. 庄海洋[9]分析了深厚软弱地基上的区间隧道在不同埋深情况下的动力响应. 董正方等[10]以地下结构在不同埋深情况下的抗震性能分析为基础，比较了反应加速度法、反应位移法、修正反应位移法和时程分析法的分析精度问题. 刘晶波等[11]分析了在Rayleigh波作用下埋深对地下结构动力反应特性的影响. 王苏等[12]采用生死单元法分析了埋深对地下结构抗震性能的影响. LI等[13]基于ABAQUS有限元平台分析了饱和土中地下结构在不同埋深情况下的地震响应特征. HU等[14-15]利用有限元和有限差分耦合方法研究了饱和砂土中的矩形地下结构在不同埋深情况下的沉降破坏和上浮破坏效应. CHIAN等[16]分析了埋深对可液化土层中地下结构整体位移的影响规律. LIU等[17]建立了描述砂土液化的广义塑性模型，并基于此分析了竖向地震作用和埋深对地下结构上浮量的影响规律. AZADI等[18]研究认为土体摩擦角、阻尼比及地下结构尺寸和埋深的增加会增大土体的液化效应，进而影响地下结构的受力性能和结构的上浮量. PITILAKIS等[19]讨论了隧道埋深、尺寸及土体参数等对隧道及邻近地上结构的影响规律. 由于计算硬件和理论的限制，已有研究大多进行部分简化处理，少见以完全耦合有效应力动力方法进行的相关研究. 本研究基于OpenSees开源程序平台和Biot动力固结理论，采用修正的多屈服面塑性砂土动力本构模型和考虑结构动力非线性的纤维截面单元，建立饱和砂土场地-地铁车站结构相互作用数值计算模型，进一步分析埋深对地铁车站结构地震动力响应的影响规律.

1 数值模型建立

砂土本构模型参考由YANG等[20]修正的多屈服面塑性本构模型，即OpenSees软件中的pressure depend multi yield(PDMY)模型. PDMY模型屈服面方程为

(1)

其中，s为偏应力张量，s=σ′-p′δ(σ′为有效应力张量；δ为克朗内克符号)；α为偏应力空间中屈服面在π偏应力平面上的中心点坐标；M表示屈服面大小，M=6sinφ/(3-sinφ)；p′为有效应力；p′0=-c/tanφ，c为黏聚力，φ为土体摩擦角.

具体地，在OpenSees中建立17 m×30 m平面应变模型，网格尺寸为1.7 m×1.0 m，土体采用四节点quadUP耦合单元，车站结构截面尺寸如图1. 模型左右边界采用“捆绑边界”，固定底边边界，地表边界为排水条件，不考虑土体与结构的切向滑移和法向脱空，数值模型如图2. 选取结构底板中部以下5.0 m处为特征点T1， 距离左墙中部3.4 m处为特征点T2.

图1 地铁车站结构横截面(单位：m)Fig.1 The cross section of subway station structure (unit:m)

土体基本物理力学参数如表1. 车站结构选用C40混凝土，配筋选用HRB400级钢筋. 车站结构采用可考虑动力非线性的纤维截面单元，钢筋混凝土纤维截面如图3. 钢筋混凝土本构模型如图4.

图2 数值模型Fig.2 (Color online) The numerical model

表1 土体主要物理参数
Table 1 Main soil parameters

密度/(kg·m-3)剪切波速 /(m·s-1)泊松比参考应力/kPa剪胀角/(°)内摩擦角/(°)压力相关参数剪缩系数1 9002000.358027330.50.07

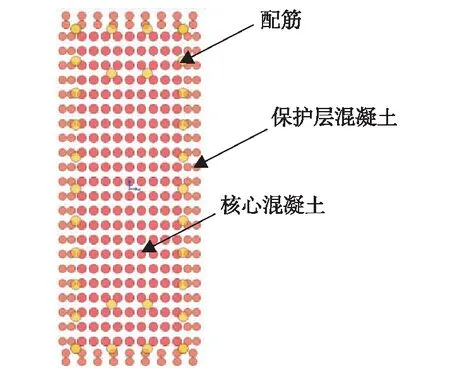
图3 纤维截面示意Fig.3 (Color online) Schematics of fiber cross section

图4 钢筋混凝土本构模型Fig.4 The constitutive model of reinforced concrete

本研究动力数值分析模型选用EL-Centro地震波，持续时间30 s，峰值强度为0.2g， 水平地震作用从底部基岩边界输入. 计算过程为：① 施加重力，进行初始地应力场分析；② 输入地震动作用进行动力时程分析. 图5为EL-Centro地震波时程曲线与傅里叶谱幅值曲线.

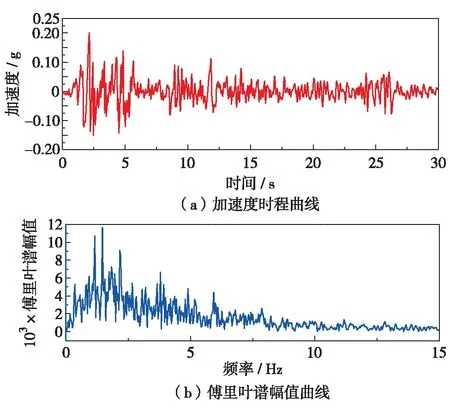
图5 EL-Centro波时程曲线与傅里叶变换谱Fig.5 (Color online) Acceleration time-history and corresponding Fourier spectra of EL-Centro earthquake wave

2 数值计算结果与分析

2.1 埋深对场地加速度反应谱的影响

图6为地铁车站不同埋深场地特征点处加速度β反应谱曲线对比情况. 由图6可见，不同地铁车站埋深条件下的场地特征点加速度β反应谱曲线均呈现双峰甚至多峰特征，且随着车站结构埋深的减小，场地特征点处加速度β反应谱曲线峰值变大，呈明显的场地放大效应，谱峰最大增幅为154%.

图6 特征点处加速度β谱曲线Fig.6 (Color online) β-spectrum curves of typical points

2.2 埋深对结构动力变形响应的影响

图7(a)和(b)分别为不同埋深条件下车站顶、底板中点水平位移差和底板中点竖向位移时程曲线，由图7可见，随着车站结构埋深的增加，结构顶、底板水平位移差极值减小，对应层间位移角极值(埋深3 m)从1/342减小到1/621(埋深12 m). 此外，结构上浮量随着车站埋深变大而显著变小，车站结构在埋深12 m时的最大上浮量仅为埋深3 m时上浮量的25%.

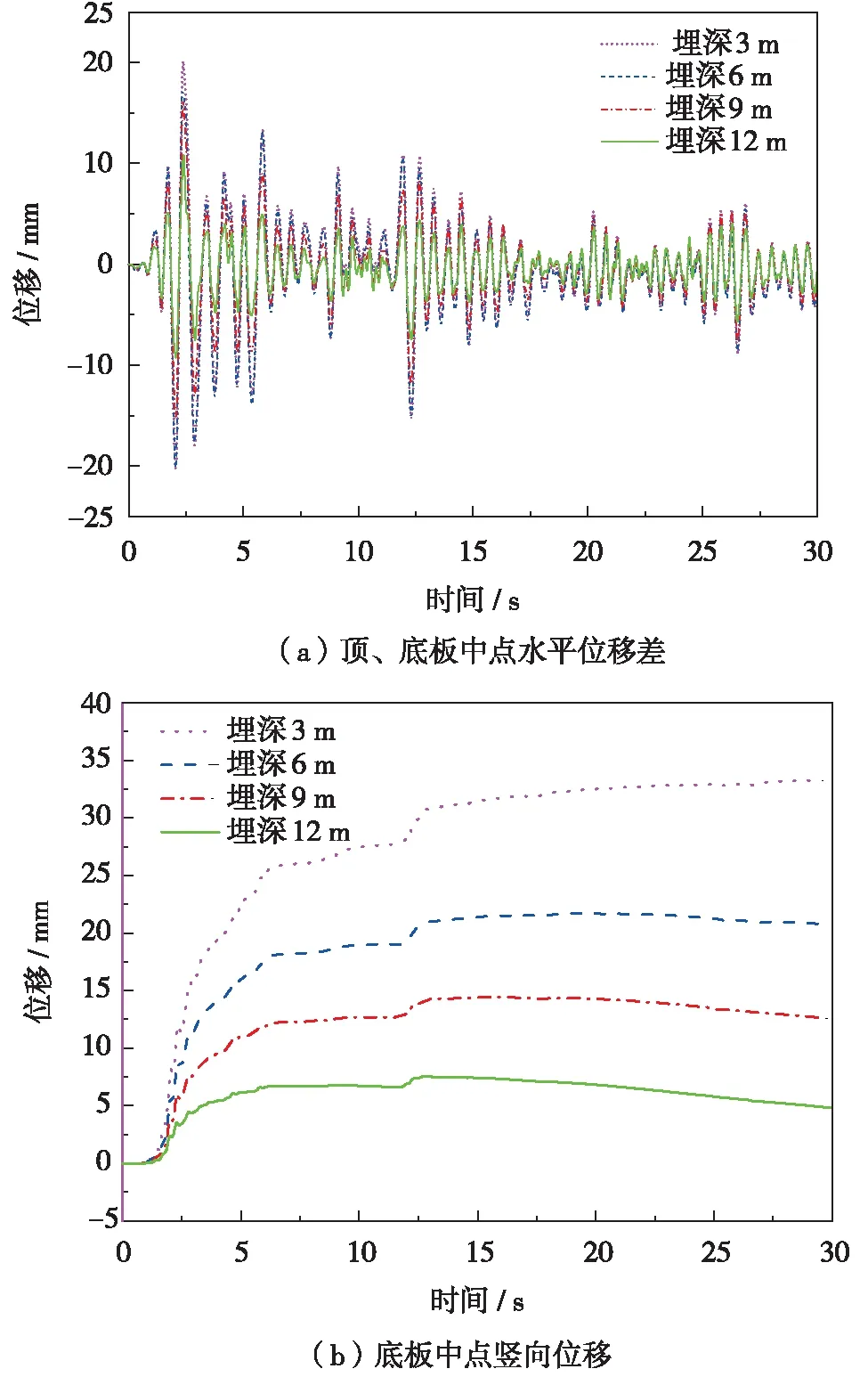
图7 不同埋深条件下车站结构位移时程曲线Fig.7 (Color online) Time-history of displacement of station structures with different burial depths

2.3 埋深对车站结构动内力响应的影响

为分析埋深对车站结构动内力变化的影响规律，选取车站结构特征截面如图8. 图9(a)为各截面动内力峰值随埋深变异系数的分布情况. 由图9(a)可见，对动轴力而言，左右墙与顶板交接处最大，其次是顶板各截面；对动剪力而言，中柱与顶底板交接截面处(P6和P10)的变异系数最大，其次是顶板截面；对动弯矩而言，中柱上下端截面(P7和P8)变异系数最大，且各截面变异系数的分布情况与动剪力相似. 由此可知，两侧墙与顶板交接处(P6和P10)和中柱上下端截面(P7和P8)为车站结构埋深变化影响的关键截面位置. 为更加清晰说明关键截面位置处动内力峰值随车站结构埋深的变化规律，现选取上述关键截面位置处进行后续无量纲化分析. 选取埋深3 m时的动内力峰值为基准值计算无量纲化指标F*，

F*=F/F3

(2)

其中，F为既定埋深条件下关键截面动内力峰值；F3为埋深3 m时关键截面动内力峰值.

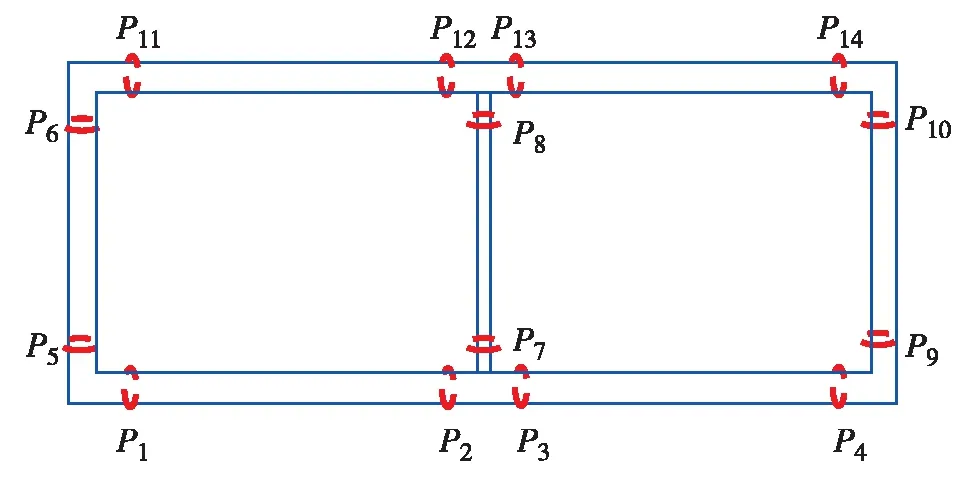
图8 地铁车站结构关键截面示意图Fig.8 (Color online) Schematic diagram of key sections of subway station structure

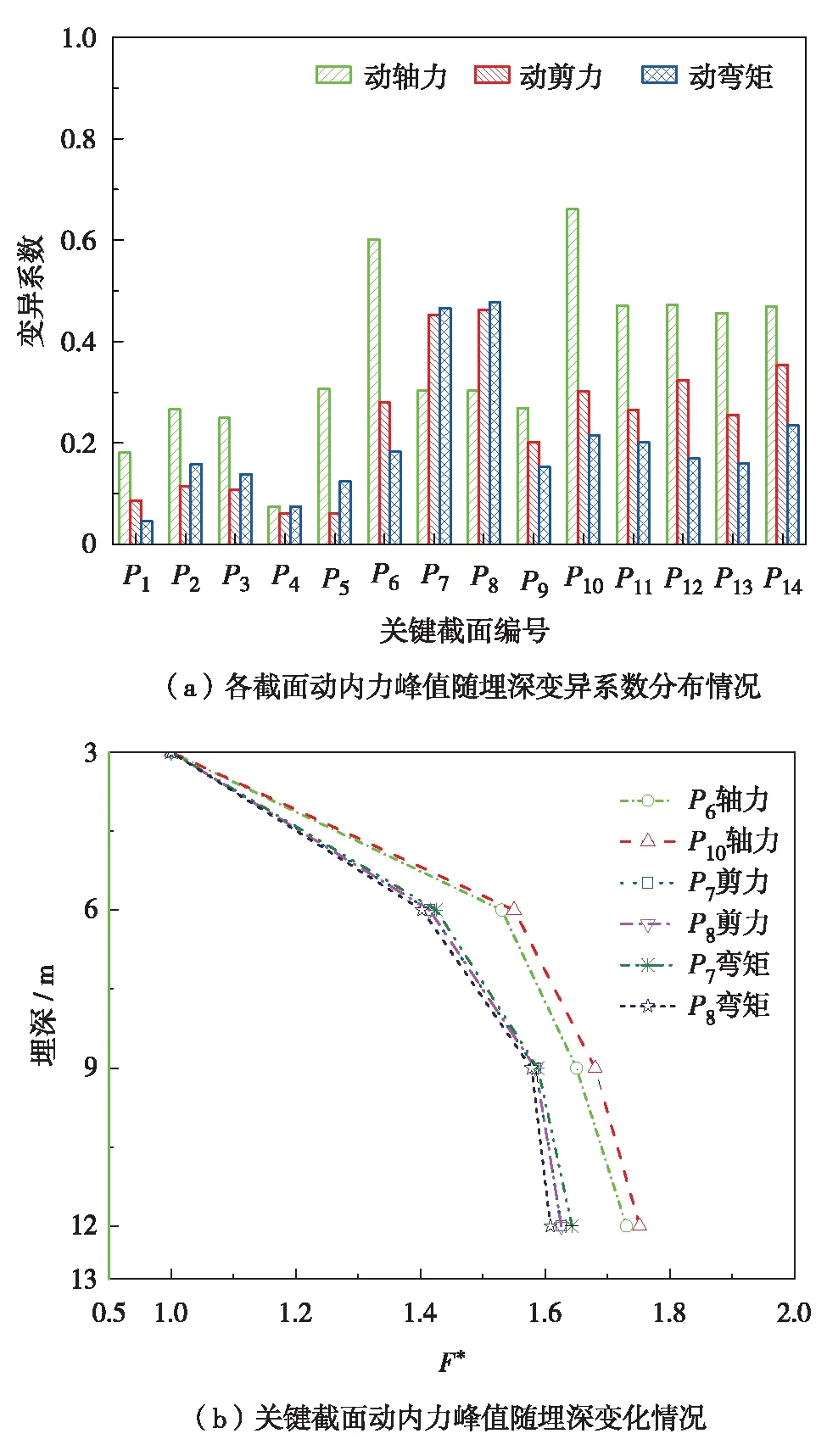
图9 不同埋深条件下车站结构动内力峰值变化情况Fig.9 (Color online) Peak values of dynamic internal forces of station structures with different burial depths

由图9(b)可见，各关键截面动内力峰值均随着埋深增加而变大，但增幅率均随车站结构埋深增大而减小. 特别地，中柱上端部截面随车站结构埋深的增幅率最大，即受车站结构埋深影响程度最为显著.

3 结 论

借助于开源程序平台OpenSees，建立了基于动力完全耦合有效应力方法的地铁车站结构-饱和砂土场地相互作用数值分析模型，分析了车站结构埋深对可液化场地中地铁车站地震动响应的影响规律，计算结果与分析表明：

1)随着车站结构埋深的减小，场地特征点处加速度β反应谱峰值变大，且各埋深工况均呈现明显的场地放大效应；

2)随着车站结构埋深的增加，结构顶、底板水平位移差极值减小，对应层间位移角极值和结构上浮量亦均呈现减小趋势；

3)各关键截面动内力峰值均随着埋深增加而变大，其中中柱上端部截面动内力受车站结构埋深影响程度最为显著.