基于EMD-LSTM的时间序列预测方法
戴邵武,陈强强,2,刘志豪,戴洪德
1)海军航空大学岸防兵学院,山东烟台 264000;2) 海军92728部队,上海 200040;3)海军92214部队,浙江宁波 315000;4)海军航空大学航空基础学院,山东烟台 264000
时间序列预测在工程实践中具有重要意义,通过对时间序列的准确预测,可对其趋势进行管理,有针对性地制定相应计划措施,把握时间序列特征,从而应对未来情形的不确定性[1].
传统的时间序列预测方法主要基于数学和统计学基础,通过对序列进行线性回归或最小二乘回归分析,建立预测数据和历史数据之间的联系.自回归移动平均(auto regression moving average, ARMA)模型作为经典的时间序列预测模型,具有严谨的理论支撑,发展较为成熟.ARMA模型从数学意义上可看做自回归(auto regression, AR)模型与移动平均(moving average, MA)模型的组合[2],其扩展形式还有自回归积分移动平均 (autoregressive integrated moving average, ARIMA) 模型等[3].传统的预测分析方法模型简单,理论精确,但针对复杂非线性非平稳时间序列的预测存在一定精度限制.
神经网络理论的成熟完善,使其在工程中取得重大应用.一些浅层的神经网络,如支持向量回归(support vector regression, SVR)在时间序列预测中具有广泛应用[4];LI等[5]采用极限学习机(extreme learning machine)对经济学中的时间序列进行预测;丁亮等[6]利用BP(back propagation)神经网络,实现自然方面的时间序列预测.浅层神经网络的局限之处在于模型过于简单,在实际训练中,模型精度制约了预测精度的提升.递归神经网络(recurrent neural network, RNN)作为一种循环反馈的神经网络框架,能够充分考虑时间序列中的相关性,通过分析历史信息,建立完整的时间序列模型[7].但在使用过程中,RNN容易出现梯度消失及梯度爆炸等问题,而长短期记忆(long-short term memory, LSTM)网络作为一种特殊的RNN模型,能够有效规避这些问题,实现对历史信息真实有效的利用[8].
复杂非线性非平稳时间序列在预测模型的构建中具有难度较大及模型不准确的问题,本研究通过经验模态分解(empirical mode decomposition, EMD)方法对原信号进行处理,以降低时间序列的复杂程度;针对EMD分解后的本征模态函数(intrinsic mode function, IMF)分量及趋势项,采用精度更高的LSTM模型分别进行预测;通过对预测结果进行汇总后,得到原始时间序列的预测结果.
1 长短期记忆网络
1.1 递归神经网络原理
递归神经网络由输入层、隐藏层及输出层构成,通过将上一时刻的状态信息传递到当前状态,从而将时间序列展开为一系列具有相互性的神经元,其结构如图1[9].其中,节点表示每一时间点上的神经元;U为输入层与隐藏层之间的权重连接;W为隐藏层与神经元之间的权重连接;V为隐藏层与输出层之间的权重连接.随着时间累加,信息在传递过程中不断损失,初始信息能力逐渐弱化,将会出现梯度消失等问题,也就丧失对时间序列的长时间处理能力.

图1 递归神经网络神经元[9]Fig.1 Structure of recurrent neurons[9]
1.2 LSTM原理
针对RNN训练过程中的梯度消失问题,LSTM网络被提出并不断完善.LSTM的主要理论是设计记忆模块,该模块可受控于多个控制门,从而实现长时间记忆功能[10].LSTM的结构如图2.

图2 长短期记忆网络Fig.2 Long-short term memory network
LSTM网络更新[11-12]为:设h为LSTM单元输出,c为LSTM记忆模块值,x为单元输入,Wxc及Whc分别为输入数据及上一时刻的输出权值,时刻t的记忆单元值为
(1)
输入门可控制当前数据输入对记忆模块状态的影响,表示为
it=σ(Wxixt+Whiht-1+Wcict-1+bi)
(2)
遗忘门可控制历史学习对当前记忆模块状态值的影响,表示为
ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf)
(3)
当前时刻记忆单元状态值为
(4)
其中,符号⊙表示逐点乘积.输出门可控制记忆模块状态值的输出,表示为
ot=σ(Wxoxt+Whoht-1+Wcoct+bo)
(5)
LSTM网络单元输出为
ht=ottanhct
(6)
2 EMD-LSTM算法
时间序列的预测需要对训练数据建立准确的预测模型,从而建立时间序列内部关系,为后续预测过程提供准确依据.工程应用中的绝大多数时间序列模型具有典型的非线性、非平稳性特征,针对这些复杂性较高的时间序列,若直接建立预测模型,很难达到预测精度要求.本研究采用EMD-LSTM算法,通过对复杂非平稳时间序列进行EMD分解,降低时间序列的复杂程度,从而完成对复杂程度较低IMF分量的LSTM建模.
EMD是一种新型的信号分解方法,在非线性、非平稳信号的处理中具有良好效果[13].EMD算法将复杂信号分解为多个IMF和1个趋势项(trend),其表达式为
(7)
其中,st为原始信号; imfi(t)为第i个IMF分量;rn(t)为趋势项.
在分解过程中,IMF分量的取值标准为:① 信号中零点数和极值点数相等或至多相差1;② 极大值和极小值包络线的均值相等且为0.
采用EMD方法进行时间序列分解后,其误差量级为1×10-14,可以完整表达出时间序列包含的全部信息,分解后的各IMF分量及趋势项组合,可以完全拟合原时间序列.对IMF分量进行特性分析可知,随着分解次数的增加,IMF的阶数不断增加,相应IMF分量的波动频率不断降低,即低阶IMF分量对应高频信号.利用EMD算法处理原时间序列,可以准确得到时间序列在不同时间段的波动特征,简化时间序列预测模型,在一定程度上提高时间序列预测精度.
文献[14]通过经验模态分解与支持向量机相结合的方法,对氢原子钟差序列进行预测分析;然而,对于工程实践中大部分复杂时间序列,其低阶(高频)IMF分量在平稳性及复杂性上虽然比原时间序列具有一定优化,但仍具有很强的波动性,此时利用普通的支持向量回归难以取得满意的预测效果.低阶IMF分量仍保留时间序列的部分信息,不能通过简单的舍弃处理进行降噪.本研究在经验模态分解基础上,针对相对平稳但仍具有较强波动性的IMF分量,构建LSTM网络预测模型,提高了预测模型的准确性及预测精度.根据EMD分解的完备性可知,分别预测后的结果符合时间序列完备性的需求.EMD-LSTM预测的整体流程图如图3.

图3 EMD-LSTM预测流程图Fig.3 Flow chart of EMD-LSTM
图3左半部分为直接使用LSTM进行预测的结果.本研究预测过程具体步骤为:① 将待分析的时间序列进行经验模态分解,得到分解后各分量(imf1、imf2, …, imfn)及趋势项rn; ② 对所有IMF分量及趋势项分别建立LSTM预测模型,并与SVR预测模型进行对比验证;③ 对各个分量进行预测;④ 将预测值累加得到最终预测值;⑤ 分析预测结果,与文献[14]中提出的EMD-SVR方法对比,验证模型可行性.
3 仿真分析
以2014-05-13至2015-09-25中国北京市PM2.5浓度数据(来自网站公开数据[15])为例进行仿真分析.受供暖等环境因素影响,原始数据序列的波动较大,复杂程度较高.气象局记录数据间隔为1 h,且有部分缺失.数据处理时将以天(d)为单位对每天的PM2.5浓度做平均值处理,同时补充缺失值,共得到501个数据点[16],如图4.

图4 PM2.5浓度数据序列Fig.4 The data series for the concentration of PM2.5
由图4可见,PM2.5浓度的原始时间序列呈现很强的非线性与非稳定性,序列的复杂程度较高.采用EMD分解方法处理原始PM2.5数据序列,以降低序列复杂程度,结果如图5.

图5 原始序列的EMD分解结果Fig.5 The decomposition result of original series by EMD
针对每个IMF分量及趋势项,构建预测模型.选取前450个数据作为训练集,余下51个数据作为测试集,以均方根误差(root mean squared error, RMSE)及平均绝对误差(mean absolute error, MAE)为指标,衡量EMD-LSTM算法对时间序列的预测能力[17].
(8)
(9)
其中,Xreal,i为数据序列中第i个数据的真实值;Xpre,i为第i个数据的预测值;n为数据点个数.
排列熵作为一种检测时间序列随机性和动力学突变行为的方法,具有计算简单、抗噪声能力强等优点.因此,可以通过排列熵来衡量信号复杂度[18],排列熵值越大,其对应时间序列复杂程度越高.根据EMD分解得到各IMF分量的排列熵如图6.

图6 序列的排列熵Fig.6 Permutation entropy of series
根据图5中EMD分解后的IMF序列及趋势项,分别构建LSTM预测模型.为对比验证,构建各自对应的SVR预测模型,选择RBF核函数及线性核函数进行时间序列预测,利用交叉验证方法确定核函数参数及惩罚参数.两种方法下各IMF分量及趋势项的RMSE及MAE计算结果如表1.
由表1及图6可见,随着IMF阶数的增加,各分量对应的排列熵逐渐降低,预测误差随之减小,证明了EMD算法对于降低IMF序列复杂程度的合理性.在表1中,由于趋势项的时间序列过于简单,因此,未进行区分对比预测.对IMF分量采用LSTM与SVR方法对比,结果表明,对于高阶IMF分量,随着时间序列复杂程度的降低,两种预测方法的差别逐渐降低,相比SVR预测模型,LSTM预测模型的优越性不断降低;对于低阶IMF,LSTM表现出良好的预测效果,预测精度较SVR有明显提高.结合对EMD算法完备性的分析,分解得到的所有子序列重构之后,与原时间序列的误差量级为1×10-14.所以,将表1中各序列的预测结果相加,即可得到原始PM2.5数据序列的EMD-LSTM和EMD-SVR预测结果,如图7.可见,EMD-LSTM预测结果更贴近真实值.
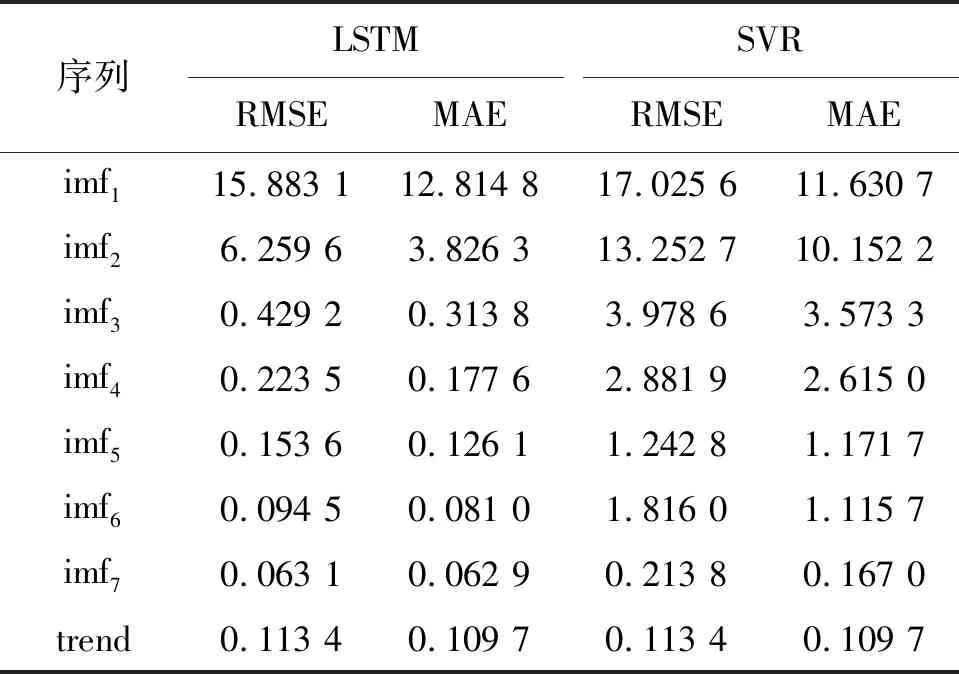
表1 各序列的预测误差Table 1 Prediction errors of series

图7 真实值及对比预测结果Fig.7 The original data and the contrast of prediction results
为验证EMD-LSTM算法的准确性,采用单个SVR模型及LSTM模型对原始PM2.5时间序列建立预测模型,并进行预测分析.将图7中得到的预测结果用数值形式进行分析,其RMSE及MAE指标如表2.
由表2可见,由于原始PM2.5数据序列的非线性及非平稳性,单一预测方法构建的预测模型不能对其进行准确预测,且由于序列的复杂程度较高,单一LSTM方法劣于SVR方法的预测效果;在利用EMD算法对时间序列进行分解之后,一定程度上降低了原序列的复杂程度,此时,对分解得到的IMF分量及趋势项采用LSTM模型和SVR模型进行预测分析,其结果比单一LSTM及SVR模型均有显著提高,证明利用EMD方法对原始时间序列进行分解的可行性.相比EMD-SVR方法而言,采用EMD-LSTM方法预测结果的RMSE降低30.95%,MAE降低26.05%,预测精度得到明显提高.

表2 四种方法的预测指标Table 2 Prediction errors of four algorithms
结 语
工程实践中的时间序列具有典型的非线性及非平稳特性,此时传统时间序列预测方法存在预测模型不精确及预测精度低等缺点,直接采用机器学习方法进行预测时,在预测精度方面也存在一定限制,影响时间序列的预测精度.本研究在对北京市PM2.5数据序列预测过程中,通过EMD方法对原始数据序列进行分解,得到与原始数据序列相关的IMF分量及趋势项,有效降低原始数据序列的非线性及非平稳性;对分解得到的IMF分量及趋势项分别建立对应预测模型,并将所得结果进行汇总分析,结果认为:① 以排列熵作为时间序列复杂程度指标,通过EMD方法对原始数据序列进行分解,可有效降低原始序列的复杂程度,有利于建立更精确的预测模型;② 与单一的预测算法对比,基于EMD的预测算法能够有效提高预测模型的准确性,从而提高预测精度;③ 针对分解后的时间序列,与SVR模型相比,采用深度学习理论中的LSTM模型具有较高的准确性,深度学习理论为时间序列预测提供理论支撑,在工程实践中具有潜在应用价值.

