幂函数变换的GM(1,1)模型在BDS卫星钟差预报中的应用研究
蒋玉祥
(西宁市测绘院,青海 西宁 810001)
0 引 言
精密单点定位(PPP)是全球卫星导航系统(GNSS)发展史上又一重大技术革命[1],由于其对于卫星精密星历轨道误差和钟差有极高的要求,所以精密星历中的轨道误差和钟差就成为了PPP一个主要的误差来源[2].根据国际GNSS服务(IGS)提供的15 min或者5 min间隔的精密卫星轨道和钟差加密得到用户所需要的精度成为一个很现实的问题.与此同时我国北斗卫星导航系统(BDS)也在迅速发展.根据IGS发布的精密星历,利用已有的方法对BDS钟差进行插值以及预报成为一个热点问题.
随着BDS的快速发展,针对精密星历的插值方法也在迅速发展,目前主要的内插方法包括了拉格朗日(Lagrange)插值、牛顿插值、三次样条插值、三角函数拟合、勒让德拟合、广义延拓逼近法等[3-8].而卫星钟差预报模型目前主要的方法有灰色理论模型[9-11]、时间序列模型[12]、卡尔曼滤波模型[13]、BP神经网络模型[14-15]、小波变换模型[15-16]、以及各种组合模型[17-22].这些预报模型针对使用情形的不同进行一定程度的改进和组合对钟差预报具有很好的实际应用价值.
为实现BDS高精度精密定位,根据BDS原子钟的特点:频率高、非常敏感、极易受到外界及其本身因素的影响,从而很难掌握其复杂细致的变换规律,而这些特点符合将系统行为特征的信息累加或者累减建立微分方程,并将累计数据还原的灰色模型.而针对普遍使用的传统GM(1,1)模型对原始数列的光滑度要求高且预测结果误差较大的问题,对BDS钟差数据用幂函数进行处理,进而提高了预测精度.本文结合BDS钟差数据利用MATLAB编程对GM(1,1)模型和幂函数变换的GM(1,1)模型进行验证,以改进传统模型的缺点和不足.
1 Lagrange插值法原理
目前,IGS只提供采样间隔为15 min或者5 min的精密卫星钟差,根据其变化的规律一般使用低阶的Lagrange插值方法即可获得满足精度要求的观测历元的卫星钟差.
首先构造n次插值多项式:
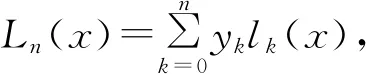
(1)
式中:lk(x)(k=0,1,…,n)都是n次多项式,称为Lagrange插值基函数.将插值基函数简化为
P(x0)=y0,P(x1)=y1,…,P(xn)=yn.
(2)
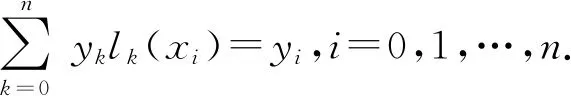
(3)
lk(x)需满足:

(4)
由此,根据n个节点xi(i≠k)都是n次多项式lk(x)的零点,故有:
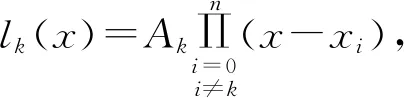
(5)
式中,Ak为待定系数,再由式(4)得到
从而得到最终结果:
(6)
式(6)就是Lagrange多项式插值的基本原理,利用BDS钟差进行插值时,自变量x为观测时刻, 因变量y为精密星历给出的该时刻的钟差.故想要获得任意时刻卫星钟差的n阶拉格朗日插值,必须至少有n+1个时刻的卫星钟差.当插值点位于插值区间的中央时,可以保证最佳的内插效果.
BDS钟差进行高精度预报时,首先用Lagrange插值根据需要进行插值,其次利用预报模型进行预报,即可得出需要的历元时刻对应的卫星钟差.
2 幂函数变换的GM(1,1)模型
针对传统GM(1,1)模型的缺陷,利用幂函数变换法对模型进行改进,以提高原始数据数列的光滑度,进而降低预报结果的预测误差.
幂函数变换的GM(1,1)模型的建模过程如下:
首先,设原始数据列为
y(0)(t)={y(0)(1),y(0)(2),…,y(0)(n)}.
(7)
对原始数据做基于幂函数的变换:
x(0)(t)={x(0)(1),x(0)(2),…,x(0)(n)},
(8)
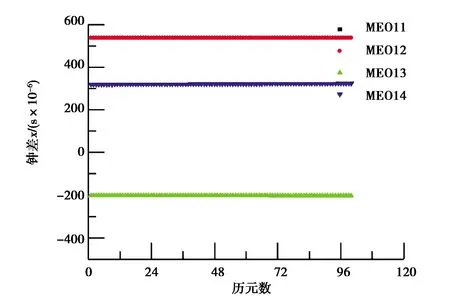
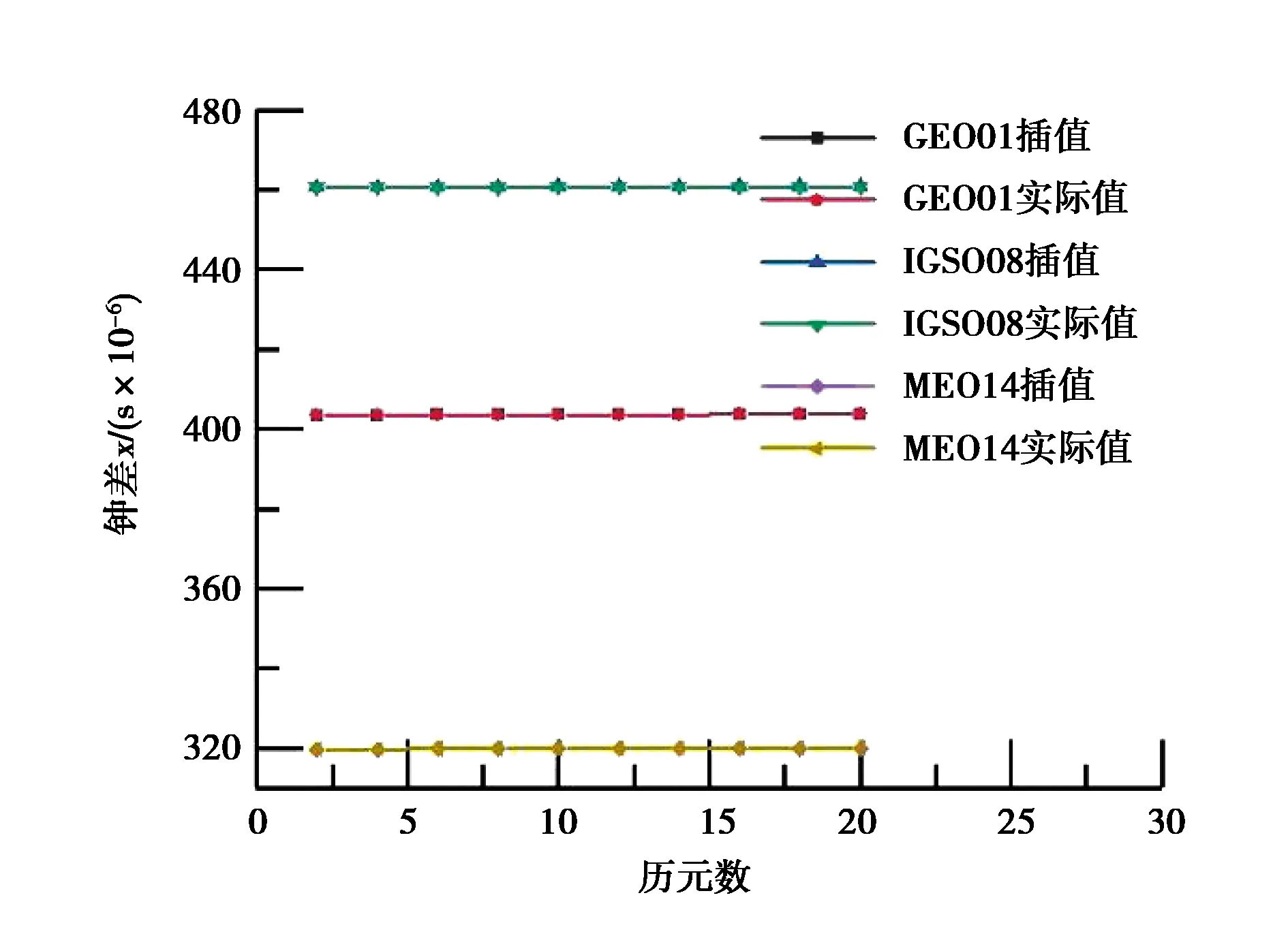
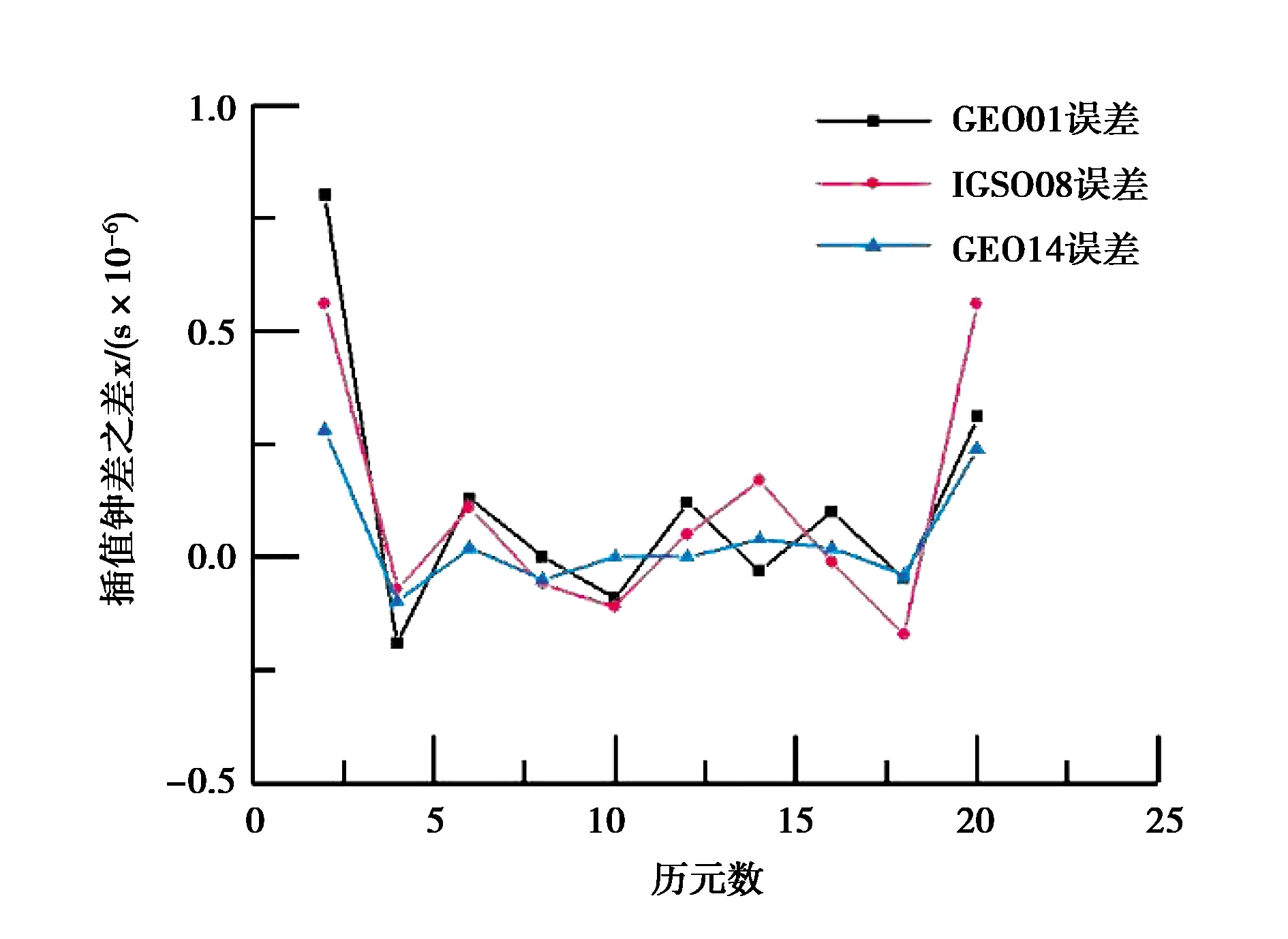
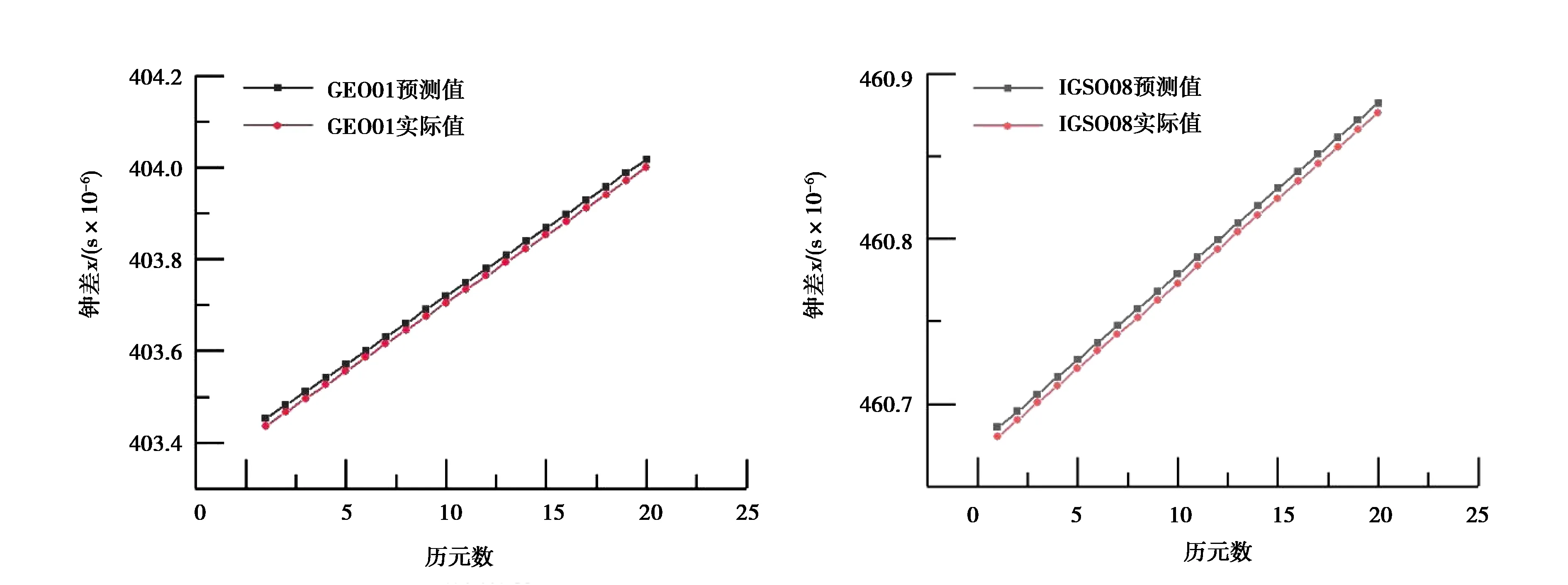
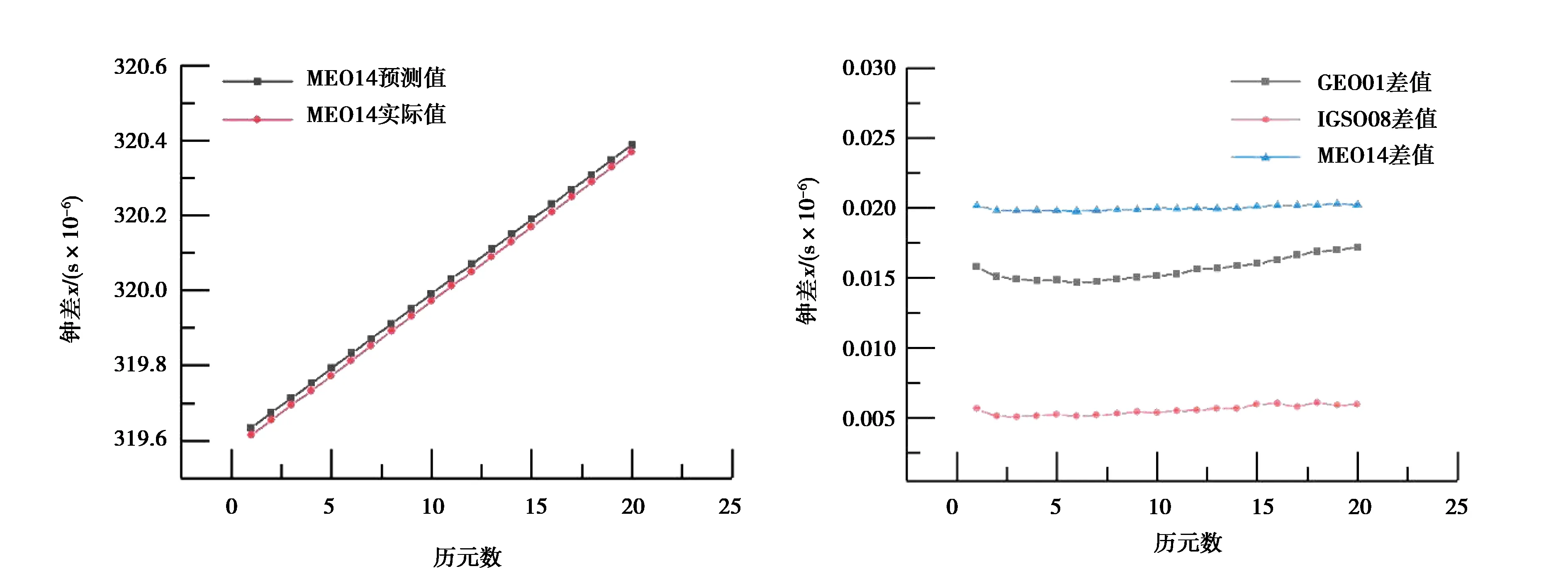
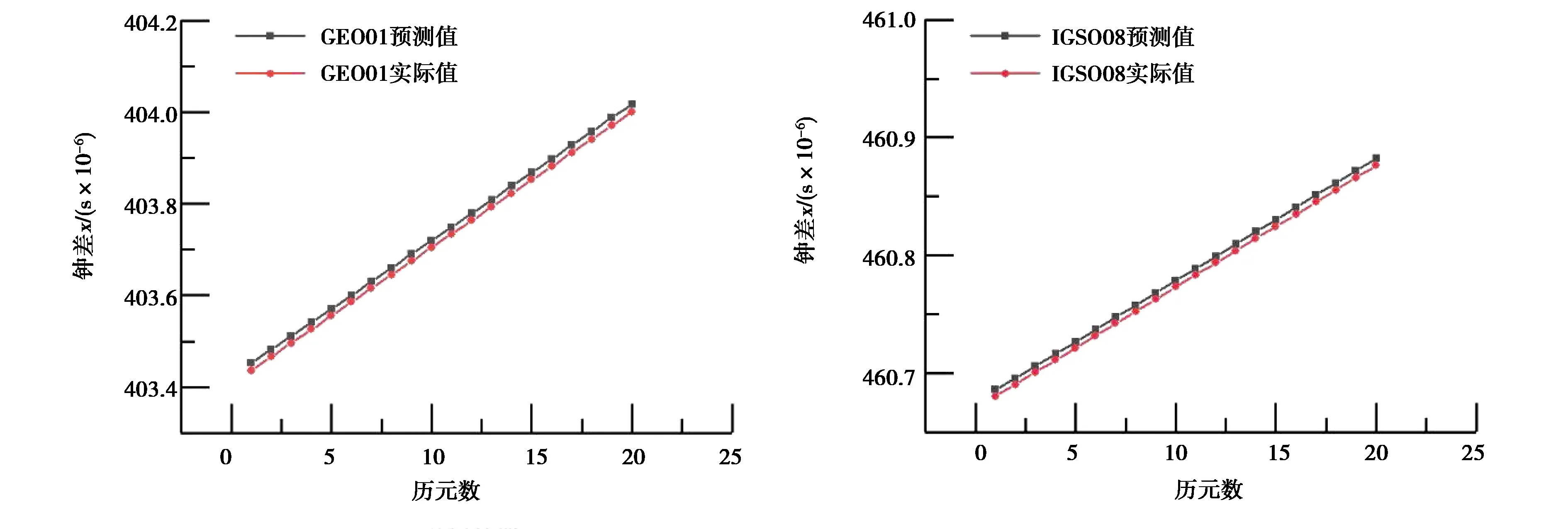
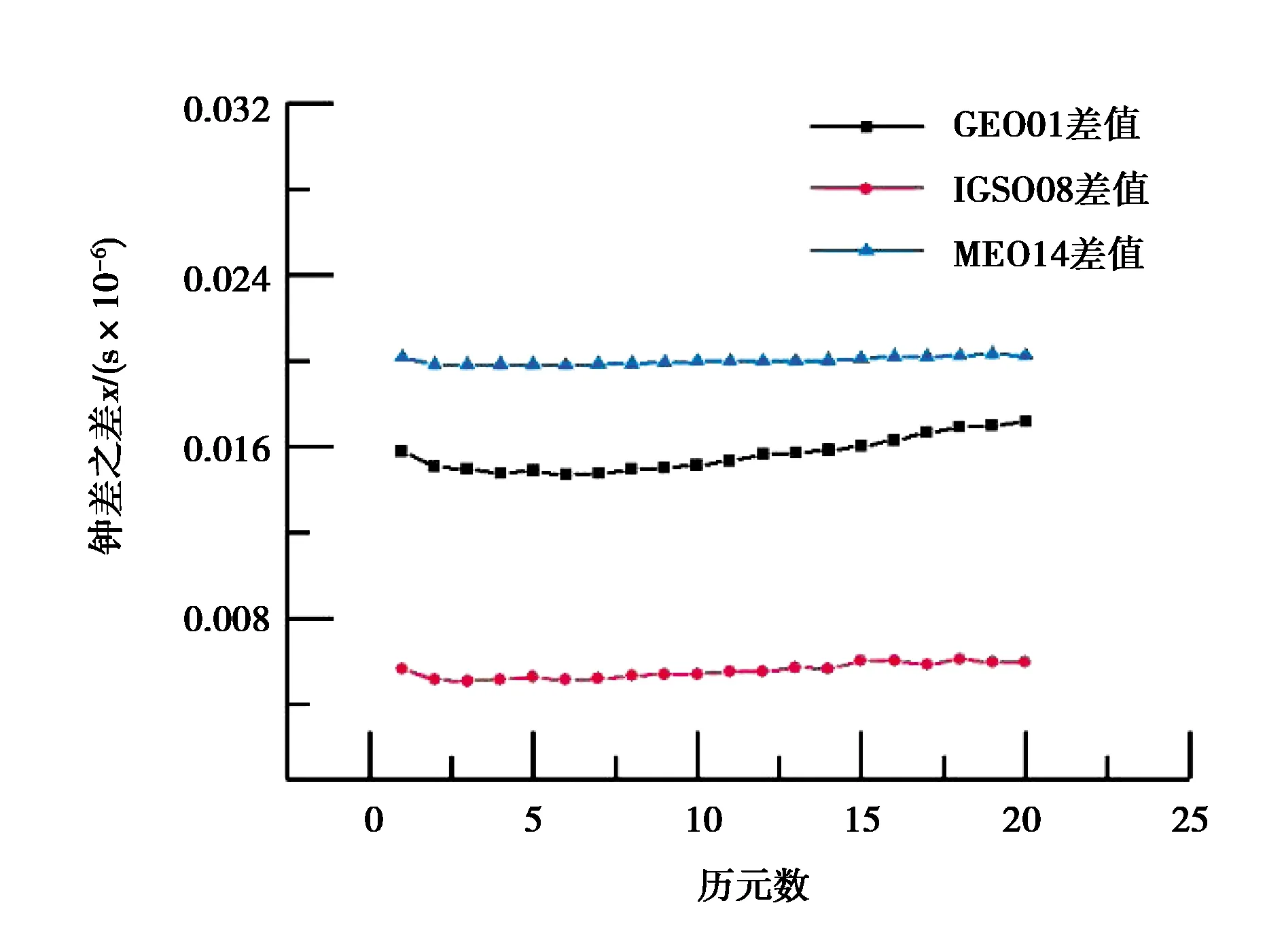
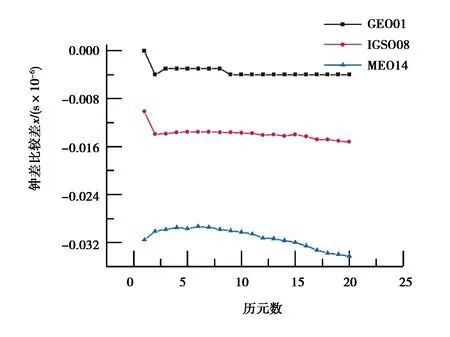
式中,x(0)(t)=[y(0)(t)]-a,t=1,2,…,n,0 其次,对x(0)(t)进行一次累加(1-AGO)生成一次累加序列: x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}, (9) (10) (11) yn=[x(0)(2),x(0)(3),…,x(0)(n)]T. (12) 将求得的参数α、u值代入时间响应函数,即可得. (13) 累减还原后得到的预测模型为 (14) 最后,将函数还原后即可得到预测数据: (15) 式中:k表示BDS卫星的某时刻;x表示对应时刻卫星钟差的幂函数变换;y表示该时刻的卫星钟差. 式(15)为利用幂函数变换改进的灰色理论模型. 数据选自NASA(National Aeronautics and Space Administration)数据分析中心(ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/)发布的多模混合数据中筛选出的2018年7月30日的采样率为5 min的BDS精密星历.数据中包含了14颗BDS卫星,其中地球静止轨道(GEO)卫星5颗(C01-C05)、倾斜地球同步轨道(IGSO)卫星5颗(C06-C10)、中圆地球轨道(MEO)卫星4颗(C11-C14).历元总数为288,采样区间为0:0:0到23:55:0.将10 min历元间隔的偶数历元卫星钟差作为将要插值的实际值,将10 min历元间隔的奇数历元卫星钟差作为插值节点,首先采用Lagrange插值,然后利用传统灰色理论模型和幂函数变换改进的灰色模型进行预报.并且将预报结果与原始观测值进行对比分析,得出最终的预测结果精度. 图1~3分别示出了2018年7月30日的BDS卫星GEO、IGSO、MEO三种卫星的偶数历元钟差统计.得出GEO卫星可利用1、4、5号卫星进行计算对比,而2、3号卫星钟差有问题,无法使用;IGSO卫星都可以作为计算对比数据;MEO卫星中12、13、14可以作为计算对比数据,而11号卫星钟差存在问题,无法使用. 图1 GEO卫星钟差统计 图2 IGSO卫星钟差统计 图3 MEO卫星钟差统计 利用Lagrange插值将BDS星历中的三种钟差分别选择一颗卫星进行插值计算,GEO卫星选择1号、IGSO卫星选择8号、MEO卫星选择14号,并且将0 min,10 min,20 min,…,110 min作为插值节点,选择10阶插值,可以得到5 min,15 min,25 min,…,105 min的插值结果,如图4所示,插值与实际值保持一致;并且将插值结果与实际值做差可以得到如图5所示结果,包含端点龙格现象在内的所有插值均满足小于10-10的结果. 图4 三种卫星的卫星钟差插值 图5 三种卫星的卫星钟差之差 根据上文的插值结果剔除端点值后,利用传统灰色理论模型和幂函数变换改进的灰色理论模型分别进行钟差预报.可以得到GEO01、IGSO08和MEO14卫星的灰色模型钟差预测值如图6~8所示.并且得出预测值与实际值的差值,如图9所示,1号卫星的差值在10-8左右,8号卫星的差值在10-9左右,14号卫星的差值可以达到10-10左右,精度满足钟差预测精度. 图6 GEO卫星灰色理论传统方法预测值 图7 IGSO卫星灰色理论传统方法预测值 图8 MEO卫星灰色理论传统方法预测值 图9 传统灰色模型预测值与实际值之差 利用幂函数改进的灰色理论模型进行预报可以得到GEO01、IGSO08和MEO14卫星的改进预测结果,如图10~12所示,可以看出1号卫星钟差预测值与实际值之差在10-8左右,8号卫星的钟差预测值与实际值之差在10-9左右,14号卫星钟差预测值与实际值之差在10-10左右,均满足预报精度要求;并且得出幂函数变换改进的灰色模型预测值与实际值的差值,如图13所示,1号卫星的差值在10-8左右,8号卫星的差值在10-9左右,14号卫星的差值可以达到10-10左右,精度满足钟差预测精度. 图10 GEO卫星幂函数变换改进灰色模型预测值 图11 IGSO卫星幂函数变换改进灰色模型预测值 图12 MEO卫星幂函数变换改进灰色模型预测值 图13 幂函数变换改进灰色模型预测值与实际值之差 图14 改进模型与传统模型钟差之差的差值 根据传统灰色模型的预测值和实际值的差与幂函数改进的灰色模型预测值与实际值的差值之差,由图14所示可知幂函数改进后的灰色模型相比原模型预测结果更加接近原始数据中的钟差.以GEO01、IGSO08和MEO14为例,得出当预测值越接近原始观测值时,则改进模型预测结果越好. 在BDS卫星钟差插值与预报中,Lagrange插值可以满足高精度计算要求;而传统GM(1,1)模型对三种卫星的钟差值预报结果都可以得到一定的精度,但由于钟差的不确定性、敏感性,导致有时候钟差的波动比较大,从而会降低传统灰色模型的预测精度,限制了其适用范围.根据幂函数做变换改进灰色模型,则有效提高了原始数据的光滑度,由此建立的灰色模型预测精度也有效提高,幂函数变换的灰色模型在钟差预报中具有实际使用意义,并且更加可靠和适用.
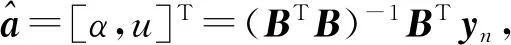
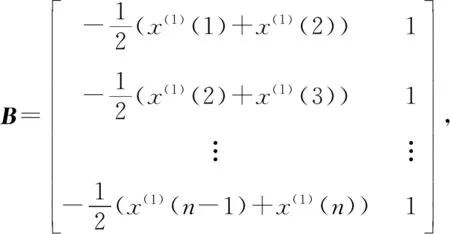


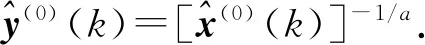
3 BDS精密钟差预报算例分析
3.1 数据来源以及统计


3.2 BDS精密星历钟差插值分析
3.3 BDS精密星历预报值分析

4 结束语

