地基伪卫星单历元三频组合逐级模糊度解算方法

匡宇龙,王玲,乐乐

(1.湖南师范大学 信息科学与工程学院,湖南 长沙410081;2.空军航空维修技术学院,湖南 长沙 410124)

0 引 言

以GPS为代表的全球卫星导航系统(GNSS)发展至今技术已经非常成熟,定位精度逐年攀升．且通过星座联合,或者与其他传感器相结合的定位系统也补足了卫星定位的部分缺陷,提高了定位系统的鲁棒性．在与GNSS相融合的系统种类中,有一类相较于其他传感器系统有着相对特殊的性质,那就是伪卫星系统．伪卫星顾名思义是类似卫星的系统,只不过并非架设在卫星上,而是架设在地面．目前随着各种定位系统的发展,星基定位系统在某些场景的弊端也逐渐暴露,例如在复杂环境下,卫星可见性较差将导致无法定位[1]．而作为星基系统的地面替代,伪卫星可以很好地胜任这一职责,而且其原理与传统GNSS并无过大的差别,无需推翻重来．而以LOCATA为代表的独立组网地基伪卫星定位系统的出现,给定位领域带来了新的思路[2]．

地基伪卫星相对于星基卫星最突出的几个特点是:架设灵活,能够在城市峡谷甚至于室内、地下停车场等场景提供导航定位;在地面的基站不受电离层和对流层的影响,能够减少靠天吃饭的弊端．

相对于广泛应用在开阔地带的传统GNSS,虽然伪卫星的传播途径中对流层时延和电离层时延影响可以忽略不计,也没有相对论时延的误差,但在地面的一个问题就是多径误差相对较重,许多学者对多径误差的检测与消除方面做了工作,可以通过载噪比加权,减轻非视距接收和多径干扰[3]并在密集城市环境下对矢量跟踪进行评估[4]．而且基站固定也会导致精度衰减因子(DOP)值不佳,接收机初始定位若固定不动,则观测量相关性太高对LAMBDA解算不利,对载波相位整周模糊度的求解是一个挑战．

多频组合算法的核心内容就是对载波观测量的整周模糊度的求解．以LAMBDA算法为代表的几何相关算法具有高效、可靠、精确等各项优势;以三频模糊度解算(TCAR)算法为代表的几何无关算法虽然仅在短基线环境下效果优秀,其原理简单,算法运算高效也是一种主流的模糊度解算算法[5]．由于星基卫星的一些固有问题,比如无法在信号被遮挡的场合提供定位服务,导航信号受到电离层以及对流层等因素影响,以实时动态(RTK)为代表的新一代定位方案虽然精度高速度快,但是受到差分站布设位置影响．作为一种地面室内等场合定位方案,地基伪卫星有能够解决上述问题的能力．

本文采取几何无关模型,利用三频观测量组合,结合伪卫星平台特性在单历元内求解整周模糊度,并在伪卫星平台验证算法的有效性．

1 双向时间同步

对地基伪卫星系统而言基于微波信道的双向时间同步技术具有较高的精度和稳定性[6]．为了使系统中的伪卫星上的时钟保持同步,传统方法是通过无线测距来实现,组网中的各个基站分别与一个位置固定且已知的站点进行测距,通过伪距值来解算钟差．但是信号传输模型的精度、接收机的位置信息,及钟漂等都会对其产生影响．通过双向时间同步法来解决问题是一个高效的选择．其原理如图1所示．

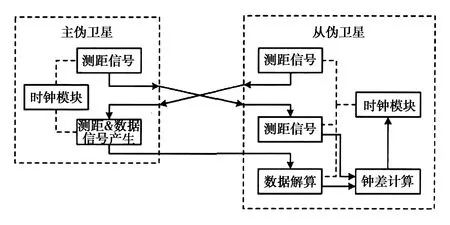
图1 伪卫星双向时间同步原理

伪距观测量和相位观测量如下:

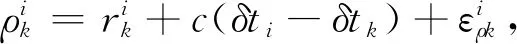
(1)

(2)

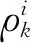
当基站和接收机位置不变，二者测距角色互换，因位置不变，故可以认为几何距离未改变。而二者的时延则发生了互换。可用公式(3)和(4)表示：

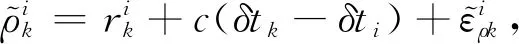
(3)

(4)

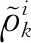
通过对比公式可以发现将式(1)与式(3)相加能够消去时延项,得式(5)．同理载波相位也可以通过式(2)与式(4)相加得到式(6)．

(5)

(6)

这就是在地基伪卫星这样一个平台上实现双向时间同步技术所带来的一个应用,由于在地基基站得以实现双向时间同步,加上电离层和对流层在地表的干扰可以忽略,不计潮汐变动以及相对论效应,故而能够达到这样一种以单差关系得到双差效果的情况．

2 基于双向时间同步的多频逐级确定法

与LAMBDA算法将双差载波相位测量值中的各个整周模糊度直接作为求解对象不同,逐级模糊度确定法(CAR)的思路是利用无几何模型通过伪距和载波组合消去几何距离项[8],基于宽巷测量值的整周模糊度比窄巷测量值的整周模糊度更容易求解这个事实出发,通过对多频测量值进行线性组合而产生的一系列不同拍频波长的组合测量值,然后沿着从最宽巷组合到最窄巷组合的顺序逐级求解出所有各个组合中的整周模糊度．可用于实时动态测量的逐级模糊度确定法在对各级双差载波相位组合测量值的整周模糊度求解运算中使用了四舍五入的取整法,整个算法呈几何无关[9]．

以双差观测量为基础的算法TCAR中消去了卫星钟差与接收机钟差,而这些钟差在地基伪卫星中由双向时间同步法已经消去．故无需将观测量进行双差计算,相当于在观测不到双差观测误差的情况下得到了消去钟差的效果．这样一来便拥有了一项提高精度的理论基础．在几何无关模型中,组合观测量的整周模糊度可以通过对浮点解取整来得到[10],逐级模糊度确定法可分为三步．

第一步:利用伪距观测量P结合双向时间同步超宽巷载波相位测量值ΦEWL,组合成几何无关公式(ΦEWL-Ρ),下标EWL表示超宽巷组合．其中Φ=λφ,表示以m为单位的载波相位观测量．

(ΦEWL-Ρ)=λEWLZEWL+εΦEWL-εΡ,

(7)

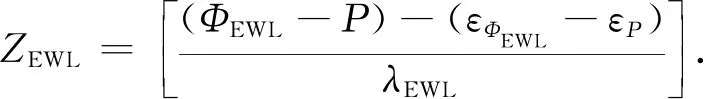
(8)

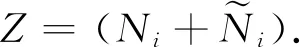
(9)

(10)

同理通过取整得到ZWL,如下:

ZWL=

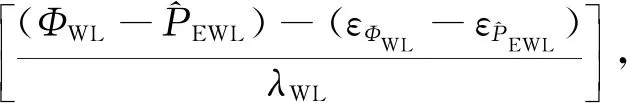
(11)

(12)

宽巷组合波长相对超宽巷更小,所以得到的精度会进一步上升．在使用得到的宽巷模糊度消去宽巷载波观测量的模糊度之后所得到的伪距值精度相较于超宽巷得到提升,为最后求解各载波整周模糊度做铺垫．

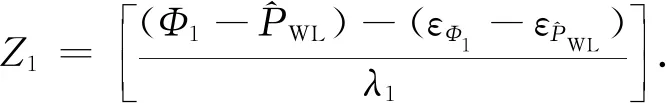
(13)

通过求得的原始模糊度加上超宽巷组合和宽巷组合的组合系数关系便可以求出其他原始频段上的原始模糊度．

3 实验分析

本实验搭建的测试环境为7个固定基站和一个沿固定轨迹移动的接收机．基站安放如图2所示,三角形表示各个基站位置．图中以(100,100,0)为圆心,半径为60 m的圆形为接收机运动轨迹．在该轨迹中采样300个点作为观测点,获得300组观测量,每组观测量包括7个伪距观测量,3×7个载波相位观测量．即在三个频段上各有2 100个整周模糊度．

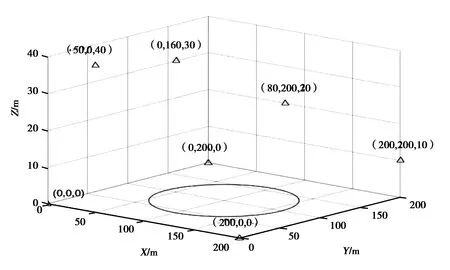
图2 基站坐标及接收机坐标

对数据的处理重心放在了对整周模糊度的固定成功率以及算法运算的时间效率,按照前述方法三步逐步展开．三个频点设置为3 122.196 MHz,2 414.28 MHz,2 537.04 MHz．为保证整周模糊度的快速解算,组合需要满足长波长,弱观测噪声等标准,超宽巷组合设置为(0,-1,1),宽巷组合设置为(1,0,-1),窄巷为(1,0,0)[11-12]．对应组合频率为超宽巷频率fEWL=122.76 MHz,宽巷频率fWL=585.156 MHz．转化为波长为λEWL=2.4438 m,λWL=0.5127 m．

程序的运算时间如图3所示,在理想环境下由于几何无关算法原理简单,计算时间非常短,在亚毫秒级．

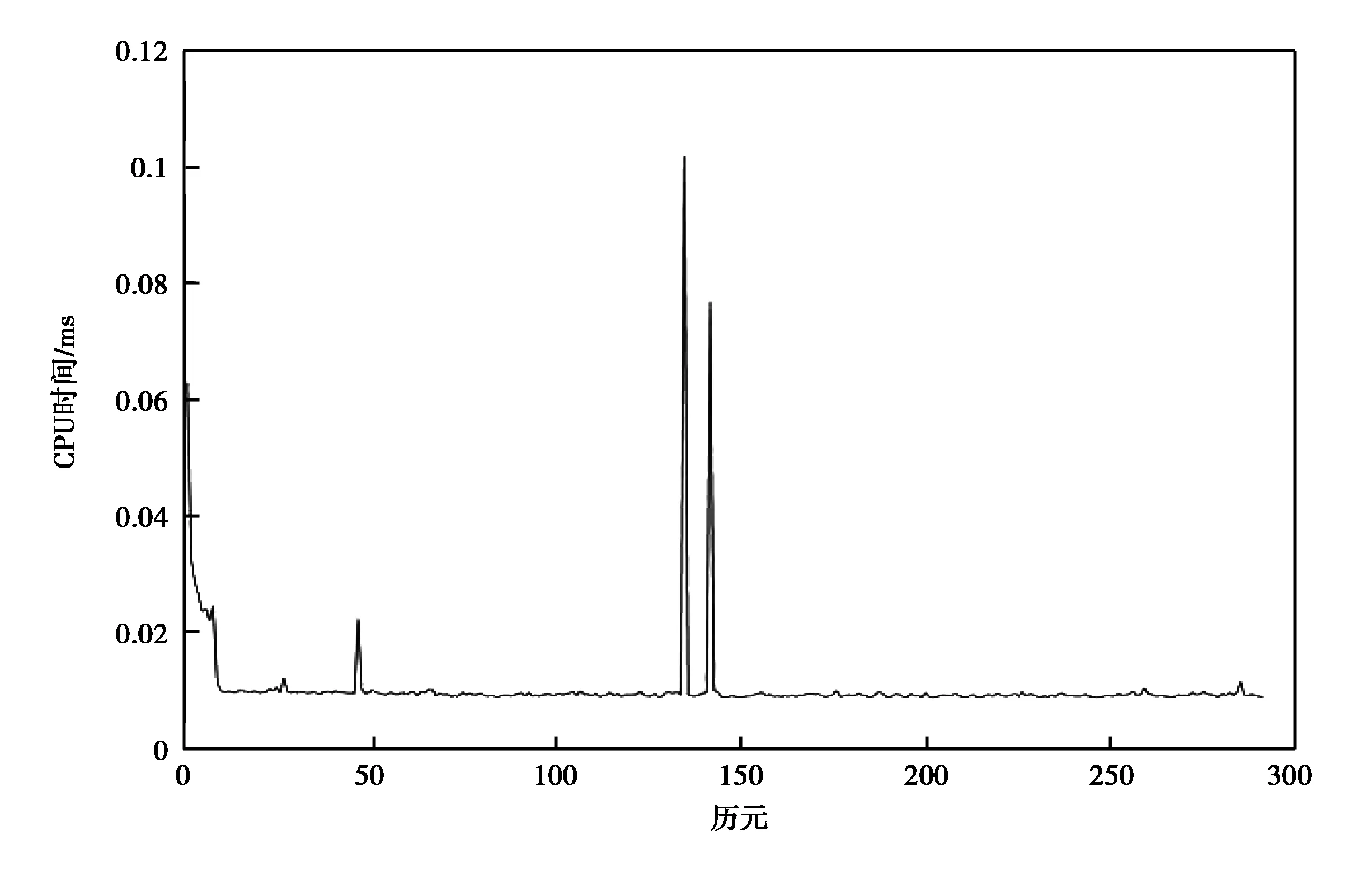
图3 算法运行时间

如表1所示,统计得2 100历元中有1 884个成功固定的历元,固定率在89.71%．可见在近距离情况下,该算法固定率虽不如传统LAMBDA算法,但是也有90%左右的成功率,且计算时间极短．

表1 算法解算结果

4 总 结

本文结合地基伪卫星的双向时间同步消去钟差的办法,加上地面信号的特点,忽略电离层和对流层干扰,能够组成类似于双差方程的公式．在此基础上利用TCAR算法在几何多样性差的情况下对整周模糊度进行求解．结果表明能够解算．

本文所采用的算法是考虑到短基线的场合,水平距离差距不大,可以忽略电离层和对流层以及其他影响星基卫星定位精度的主要误差．当面对长距离场景,可能不再能忽视电离层等误差,且由于未采用差分消去电离层误差项,采用的多频组合也并非电离层无关模型．本实验并未对长基线场合下引入电离层误差的可能性进行验证．但如同星基卫星,几何无关算法不适用于长基线的可能性仍然存在．可以考虑在超宽巷和宽巷解算出模糊度之后,利用求得的组合模糊度结合LAMBDA算法进行搜索求解原始载波的模糊度．