基于高斯粒子滤波的CPHD多目标跟踪平滑算法

谢兴祥，黄鸿柳，韦洪锦，曾箫潇

（1.哈尔滨工业大学（深圳）电子与信息工程学院，广东深圳 518055；2.广西科技师范学院数学与计算机科学学院，广西来宾 546199）

0 引言

近年来，基于随机有限集（Random Finite Set，RFS）的多目标跟踪方法受到了研究人员的广泛关注，该方法将目标状态集合和传感器量测集合分别建模为随机有限集合。RFS理论将多目标跟踪问题描述为贝叶斯滤波问题，解决了传统多目标跟踪方法中出现的数据关联以及目标数目变化的难题。势概率假设密度滤波（CPHD）是Mahler在概率假设密度滤波（Probability Hypothesis Density，PHD）的基础上提出的，CPHD滤波是一种广义的递归PHD滤波，能够改善PHD滤波在对目标数目进行估计时容易出现高阶势分布信息丢失的缺陷。CPHD能够联合传播后验强度函数和后验势分布函数，可根据物理空间描述法推导出CPHD滤波的具体实现公式［1］。

Nandakumaran等［2-3］于2007年提出PHD平滑算法，并将它基于SMC实现和高斯混合（Gaussian Mixture，GM）实现。在一个由虚假的量测、不确定的检测和数据关联所构成的多目标场景中，目标状态的数量以随机的方式随时间变化，这使得滤波和平滑方法在多目标检测中极具挑战性。文献［4］提出了一种概率数据关联（Probabilistic Data Association，PDA）多目标平滑算法，以改善在杂波中的跟踪性能。文献［5］提出一种交互式多模型平滑算法，以提高机动目标的跟踪性能。文献［6］提出一种将固定滞后平滑，交互式多模型（Interacting Multiple Model，IMM）以及概率数据关联相结合的方案，以提高在杂波中对灵敏目标的跟踪性能。文献［7］提出了在IMM-MHT中利用固定区间的平滑算法，用以提高机动目标的跟踪性能，这些技术都是针对线性高斯模型而提出来的，但可以通过诸如SMC，线性化和无迹变换技术扩展到非线性非高斯模型。学者Vo在线性高斯假设下，提出一种PHD平滑器的闭式解，为一个通用的后向递归公式严密地推导出其解析解［8］。

平滑算法可以这样描述，在随机系统估计中，滤波、平滑和预测是三个重要的相关联问题，其本质上等于计算

文献［9］提出高斯粒子滤波器（GPF），将未知状态变量的后验分布近似为高斯函数，迭代存储目标状态的均值与协方差，可以显著降低运算的复杂度，但在目标数估计上改善有限［10］。基于上述分析可知，基于粒子滤波的SMC-CPHD-TBD算法［11］在检测和跟踪未知数目的弱小目标时，一方面，目标状态需要通过计算复杂的聚类方法获得，信号较弱时跟踪精度下降，另一方面，由于粒子滤波存在粒子退化、采样枯竭等问题，虽可扩大粒子支撑集以解决，但却以牺牲时间为代价，导致在实际应用中受限较大。

针对上述问题，本文提出了将CPHD基于GPF实现，并将其与平滑算法相结合，得到GPF-CPHD平滑算法。其内涵是利用高斯函数近似目标状态的后验概率密度，采用粒子滤波的方法迭代更新CPHD中各高斯项的均值与协方差，依据CPHD目标势分布的意义，推导出粒子权重更新表达式。仿真实验验证了算法的有效性和可行性。

1 问题描述

考虑目标在一个二维运动场景中运动，目标的状态方程和量测方程分别描述为：

其中状态模型f（·，·）和量测模型h（·，·）均为已知。vk-为过程噪声，wk为量测噪声。根据量测方程，累积直到时刻k的量测序列Z：k，然后从该序列中估计出目标数目和目标状态。

Vo等在随机有限集理论的基础上将多目标跟踪问题表述为对多目标状态Xk和量测的滤波问题［12］。其中Xk为时刻k多个目标状态的集合，为时刻k多个目标量测的集合，分别记为：

其中：Kk为杂波集，Θk为一个目标产生的量测。

上述多目标跟踪滤波问题可表述为寻找一个最优多目标后验概率密度问题。假设时刻k-的多目标后验概率密度pk-（·）已知，则时刻k的多目标后验概率密度可通过多目标贝叶斯递归公式求得，即

2 GPF-CPHD平滑算法的推导

2.1 GPF-CPHD的预测

CPHD以递推形式同时传递概率假设密度函数、目标数量的概率分布及其概率母函数，可以更准确地估计目标的数量，但计算复杂度更大［13］。CPHD相比PHD能够更完整地保留目标个数的统计信息，现对目标的势分布和目标强度函数分别预测如下：

CPHD 预测步［14］：

预测势分布为

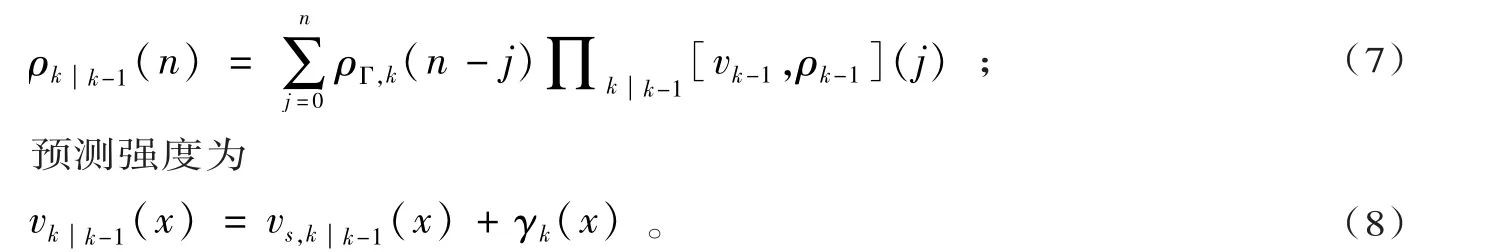
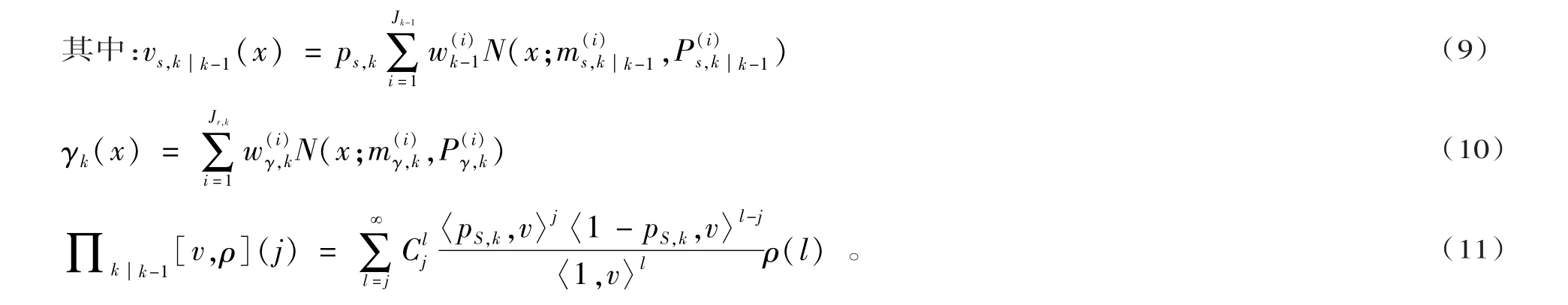
2.2 GPF-CPHD的更新

CPHD更新步：

更新势分布为

Zk为时刻k的量测集，gk（·为时刻k单一目标的量测似然函数，pD，k（x）为时刻k的目标检测概率，κk（·） 为时刻k杂波量测强度，pK，k（·） 为时刻k杂波势分布。

2.3 GPF-CPHD平滑步

由文献［15］得到CPHD基于高斯混合实现的平滑步：

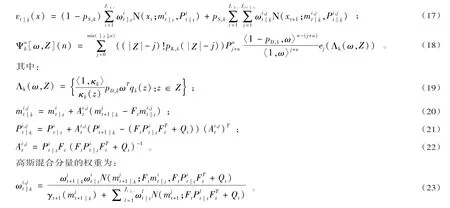
式（17）即为GM-CPHD滤波器的平滑公式。

GPF作为粒子滤波的一种推广方法，在算法实现过程中避免了粒子重采样，减少了采样的粒子数目，在预测和更新步只需迭代目标状态的均值和协方差，在保证跟踪性能的同时，可以减少计算的复杂度。GPF是采用高斯函数来近似目标状态的后验概率密度，而将其应用于CPHD的实现提高了多目标跟踪的运算速度和跟踪效果。GPF基于粒子滤波实现通过计算高斯函数中的均值和协方差估计出目标状态的后验概率密度。

2.3.1 状态预测

新生目标γi（x） ，i=，，…，Jγ，k，===分别为新生目标高斯项的均值与协方差。存活目标vs，kk-（x） ，i=，，…，Jk-，采用拟蒙特卡洛高斯粒子采样可得

pS，k（ζ） 为时刻k目标存在概率，fkk-（·） 为时刻k的单一目标转移密度，γk（·） 为时刻k新生目标强度，ρΓ，k（·） 为时刻k新生目标势分布。为第个粒子的权重分别为存活目标高斯项的均值和协方差。

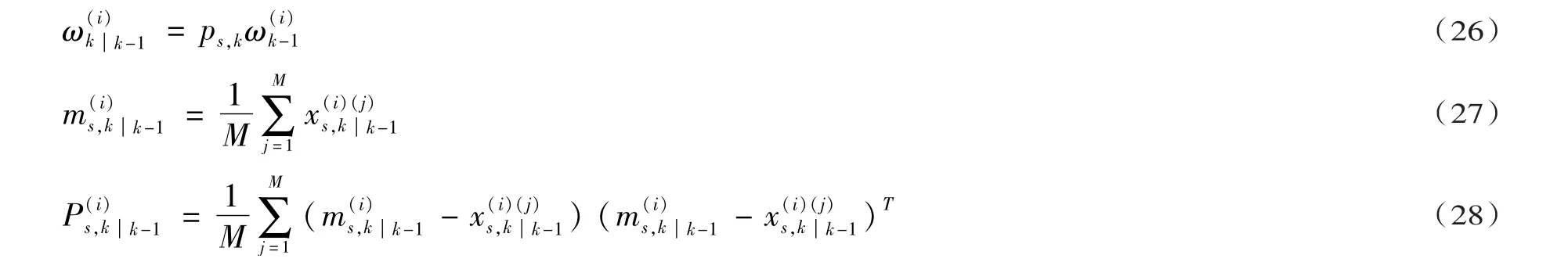
2.3.2 状态更新

在对后验强度vk（x）用高斯混合形式表示时，多目标状态的提取比PHD滤波的粒子滤波实现算法容易，因为构成高斯分量的均值实际上是后验强度vk（x）的局部极大化值，但此时需利用“修剪”技术除去高斯混合形式中含有较低权重和方差的高斯分量，并利用“合并”技术将那些比较密集的高斯分量进行合并，当从个后验强度vk（x）中提取多目标状态时，便可得到较近似的状态估计值。上述求出的高斯混合强度为vt|k（x），其相应的目标期望数可通过对目标权重求和获得，即

3 仿真实验及分析

3.1 仿真实验

为了验证GPF-CPHD平滑器的性能，将在一个杂波环境下含有4个目标的二维目标运动场景中进行仿真实验，实验模型为一个线性高斯运动模型，目标运动状态方程为

vk为过程噪声且为零均值高斯白噪声，传感器采样间隔T=s，测量时间长度为40 s。

传感器量测模型由噪声的距离和方位量测构成，即由下式表示：

其中，量测噪声wk为零均值高斯白噪声，目标存活概率为0.99，目标检测概率为0.9。杂波是一个服从泊松分布的随机有限集，且杂波平均数为3［（m）-］。

目标的运动轨迹如图1所示。

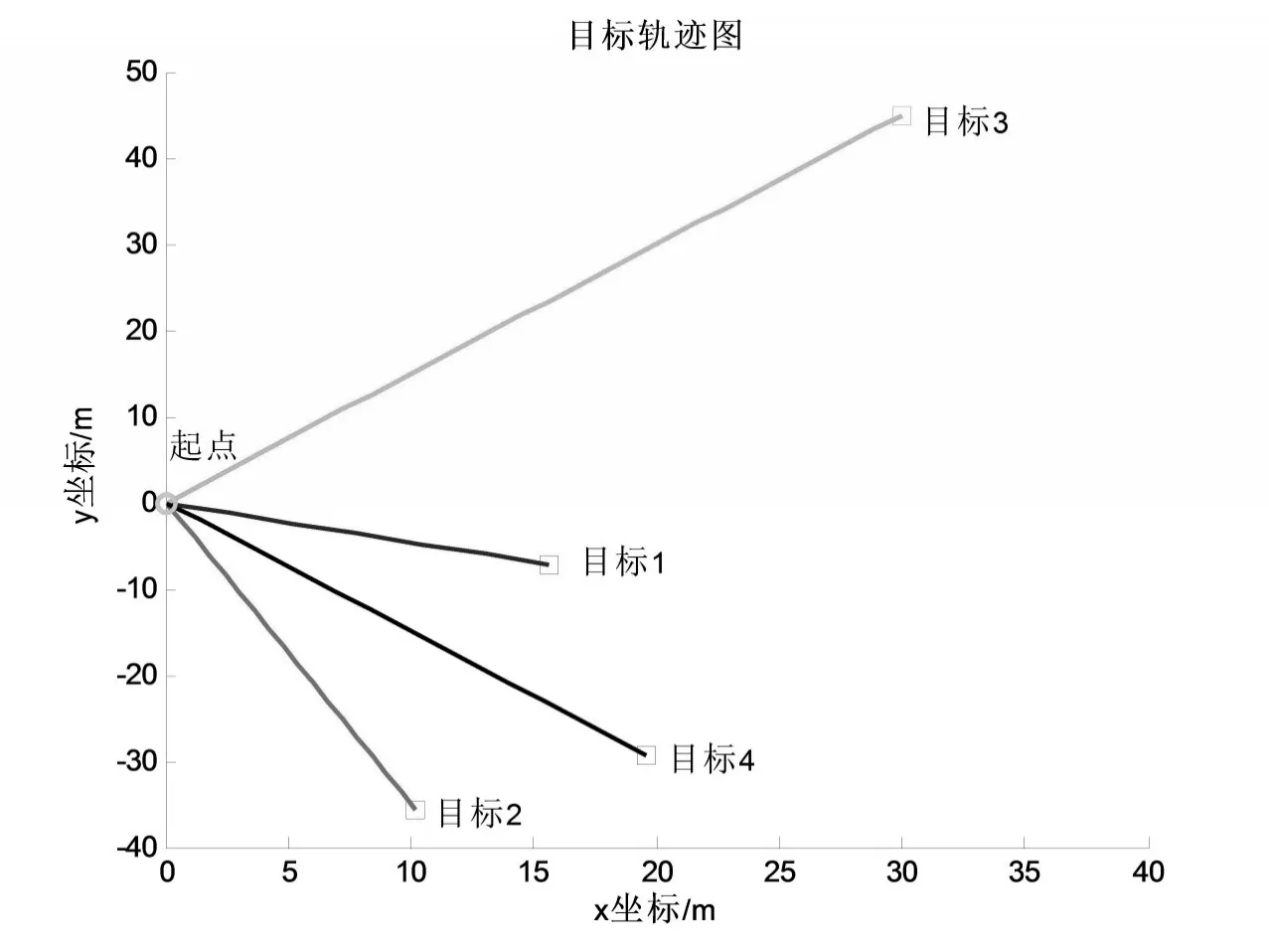
图1 目标真实运动轨迹（“○”表示起点，“□”表示终点。）Fig.1 Real target trajectories

图2为两种滤波器对目标真实数目估计的对比图。从图2可看出，GPF-CPHD平滑器估计目标数目的性能优于GPF-CPHD。这是因为CPHD滤波结合平滑算法综合利用了t时刻前后的PHD滤波估计信息，其次CPHD滤波能够在传播后验强度函数的同时，也能传播后验势分布函数，改善了PHD滤波在对目标数目进行估计时容易出现高阶势分布信息丢失的缺陷。虽然对目标的估计有滞后现象（在开始和结尾都存在），但总体来说，GPF-CPHD平滑器的检测性能还是比未经平滑处理的GPF-CPHD要稳定。

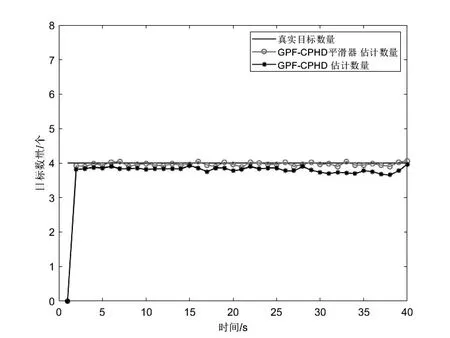
图2 目标真实数目估计图Fig.2 Estimation of real target numbers

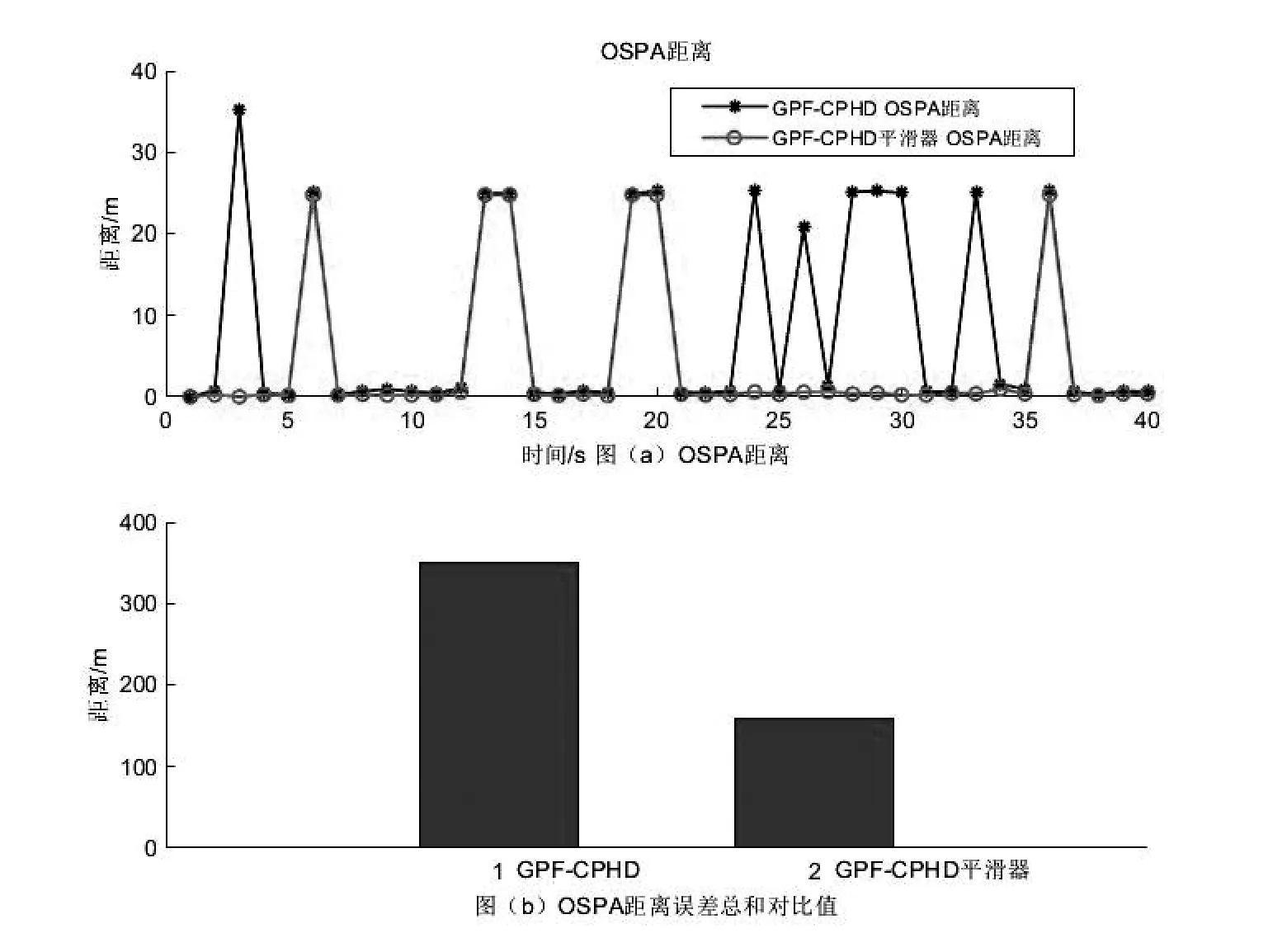
图3 OSPA对比图Fig.3 Comparison of OSPA

选用最优子模式分配（OSPA）距离［16］作为评价准则指标，OSPA包括位置和集合势两部分距离。图3用OSPA度量表征2种滤波器的性能差异。当OSPA度量距离越小，表明滤波算法的精度越高，OSPA中的参数值设为c=100，p=。从图3（a）可看出，GPF-CPHD平滑器优于GPF-CPHD；从图3（b）可进一步看出，GPF-CPHD平滑器的OSPA距离误差总和值要少于GPF-CPHD。这是因为GPF-CPHD平滑器结合GPF的特点，使用拟蒙特卡洛采样，使得采样的粒子数目更加均匀，每一个高斯项只需分配20个粒子就可以完成对目标的跟踪，减少了计算量，提高了跟踪精度。并且经过平滑处理后，能够充分利用原始量测数据，使得跟踪效果更好。

4 结束语

本文提出基于GPF-CPHD的多目标跟踪平滑算法。算法根据CPHD目标势分布的意义，结合GPF的特点，推导出粒子权重更新表达式，同时利用高斯函数近似目标状态的后验概率密度，采用粒子滤波的方法迭代更新CPHD中各高斯项的均值与协方差，避免粒子枯竭，减少计算复杂度。不足之处是与平滑算法相结合，综合利用了t时刻前后的PHD滤波估计信息，弥补了PHD滤波容易丢失高阶势分布信息的缺点，进一步改善了多目标状态估计性能但仍会出现跟踪滞后现象，这是下一步工作所要完善的。