RC和RL一阶电路响应的仿真分析及实验实现
蓝海江
(广西科技师范学院机械与电气工程学院,广西来宾 546199)
0 引言
电路分析(或电路)课程是电气类、电子信息类专业的专业核心课程。该课程理论性强、概念抽象。对于许多普通院校学生而言,该课程是一门难度系数较高、比较枯燥的课程,因此,教学效果不容乐观[1]。为了提高该课程的教学效果,与时俱进地进行教学改革[2-4],势在必行。
存在电容、电感的电路称为动态电路。由于描述动态电路的方程为微分方程,而且动态电路的过渡过程非常短暂,教学实践表明,许多普通院校学生难以理解其中的物理内涵,而基于计算机仿真辅助教学,是帮助学生突破这些瞬态困惑的有效手段[5-7]。
电路方程为一阶常微分方程的动态电路,称为一阶电路。RC和RL一阶电路的零输入响应及零状态响应,是动态电路的基本内容,因而成为仿真分析、研究的热点[8-10]。但是,由于RC和RL一阶电路互为对偶电路[11],并且RL一阶电路响应实验较难实现,因此,纵观RC和RL一阶电路响应的仿真分析及其实验研究的报导,RC一阶电路响应较为常见,而RL一阶电路响应则较为鲜见。
尽管一阶电路是最为简单的电路,但许多普通院校学生在理解上一直有困难[12]。为了帮助学生能够直观观测动态元件的动态特性,深入理解动态方程的物理内涵,本文以RC和RL一阶电路响应为例,首先,基于NI Multisim14.0软件仿真这些电路的响应,并依据仿真结果测量电路的时间常数;然后,基于模拟电路实验箱搭建实验电路,实现实验比较与验证。
1 一阶电路响应及其时间常数
1.1 RC和RL一阶电路的零输入响应
激励为零,由电路动态元件初始状态产生的响应,称为零输入响应。RC和RL一阶电路零输入响应的一般表达式为[13]

式(1)中,f(0+)为初始值。对于RC电路,时间常数τ=ReqC;对于RL电路,时间常数τ=L/Req;Req为t≥0时,移去动态元件后,单端口网络的除源等效电阻。
1.2 RC和RL一阶电路的零状态响应
动态元件初始状态为零,由激励产生的响应称为零状态响应。RC和RL一阶电路零状态响应的一般表达式为[13]

式(2)中,y(∞) 为稳态值。
1.3 一阶电路时间常数的测量方法
由于动态元件参数的限制,一阶电路的时间常数通常很小,较难测量[14]。一阶电路时间常数的测量方法有电压对称法[15]、时标法[16]及连续积分法[17]等。
把t=τ,代入式(1)、式(2)得

式(3)表明,经过时间τ后,动态元件的零输入响应为其初始值的0.368倍;式(4)表明,经过时间τ后,动态元件的零状态响应为其稳态值的0.632倍。据此,可利用时标观测法,测量电路的时间常数。
2 RC和RL一阶电路响应的仿真分析
2.1 RC和RL一阶电路响应的仿真
本文使用NI Multisim14.0作为仿真软件。该软件具有丰富的仿真分析能力。为了便于实现实验验证,仿真元件的参数设置,基于常用、低值的电子元器件。
RC和RL一阶电路响应的仿真电路如图1(a)、图1(b)所示。其中,信号发生器XFG1的参数设置为:方波,20Hz,10Vp,占空比50%;为了便于观测,偏置设置为10V。Uc、IL为网络名称。为隔离电阻,隔离后,通过示波器XSC1能同时观测到输入的激励波形和电路的响应波形。
当然,使用示波器电流探头,能更加便捷探测电流,但会增加实验成本。为了便于实验实现,本文利用取样电阻来间接地观测电感电流。
当激励方波的周期T,满足T/2≫5τ时,方波的上升沿相当于零状态响应的正阶跃激励信号,方波的下降
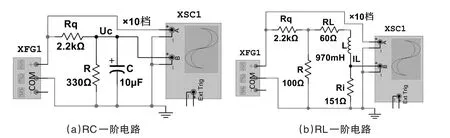
图1 RC和RL一阶电路响应仿真电路
沿相当于零输入响应的负阶跃激励信号[18,19]。据此,本文利用信号发生器输出的方波,模拟激励信号。
由图1(a)可知,RC一阶电路的时间常数为,τC=ReqC=2.870m s;忽略Rq的影响,则τC≈3.300m s。由图1(b)可知,RL一阶电路的时间常数为,τL=L/Req=3.163m s;忽略Rq的影响,则τL≈ 3.119m s。
激励方波的频率为20Hz,周期T=50m s,显然,满足T/2≫5τ的要求。
点击仿真运行按钮,即获得对应的仿真结果,如图2所示。
由图2(a)和图2(b)可知,在方波(A通道)的激励下,在仿真示波器上,可直观地观测到RC和RL一阶电路的响应波形(B通道)。
图2中,零状态响应的正阶跃激励信号与方波上升沿对应,零输入响应的负阶跃激励信号与方波下降沿对应,因此,B通道的AB段为RC或RL一阶电路的零状态响应曲线,B通道的BC段为对应的零输入响应曲线。
由图2可知,RC和RL一阶电路响应的波形相似,但是,图2(a)的响应曲线为电容C两端的电压波形,图2(b)的响应曲线为电感L的电流波形。
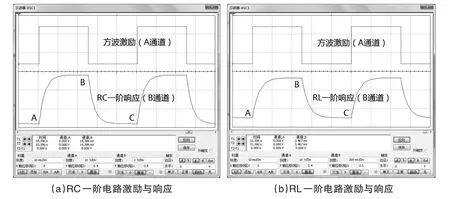
图2 RC和RL一阶电路响应仿真结果
2.2 RC和RL一阶电路时间常数的瞬态分析测量
由于一阶电路的时间常数通常很小,因此,利用实物实验较难精确测量。而利用计算机仿真,则可便捷、精确地测量电路的时间常数。
本文利用NI Multisim14.0软件的瞬态分析功能,测量RC和RL一阶电路的时间常数。
如图1,搭建仿真电路后,选择“仿真”菜单中的“Analyses and simulation”项。在其对话框中,单击“瞬态分析”项;在相应栏目中设置参数后,单击“Run”按钮,即出现瞬态分析结果。
RC和RL一阶电路响应的瞬态分析结果,如图3所示。其分析参数相同:起始时间0.045s,结束时间0.095s,其它取默认值。输出变量:RC电路为V(uc),RL电路为V(IL)。
由图3可知,依据瞬态分析结果,也可观测RC和RL一阶电路响应的动态过程。
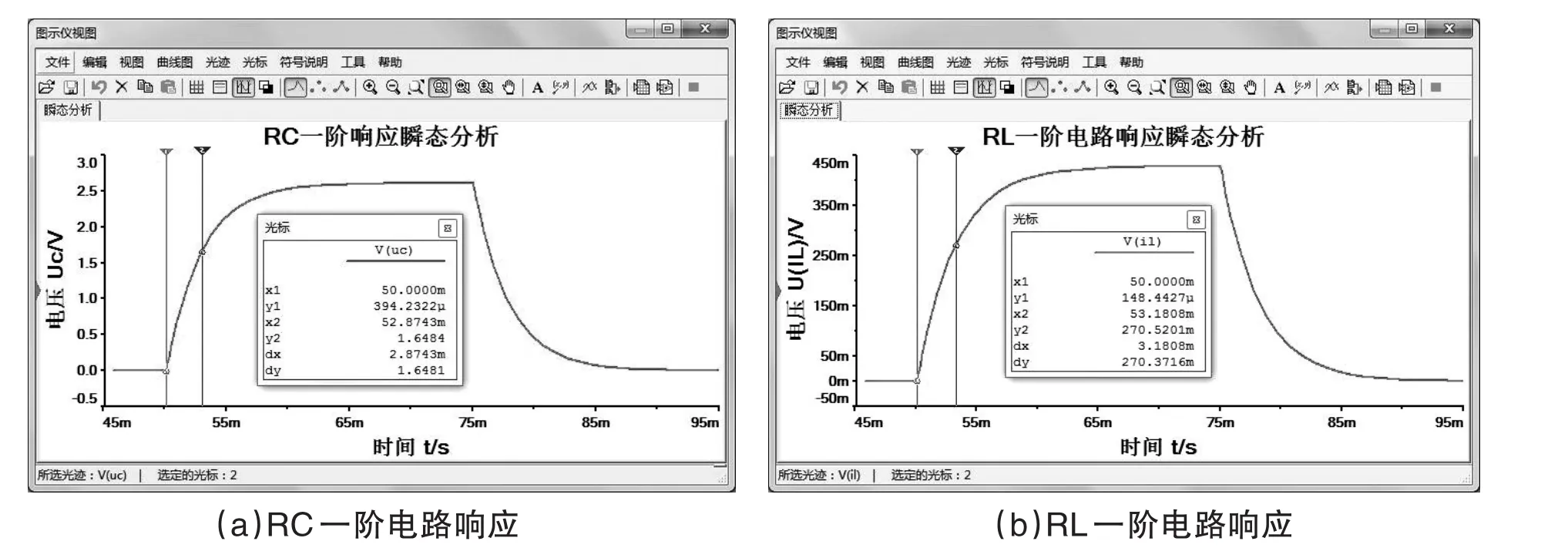
图3 RC和RL一阶电路响应瞬态分析仿真结果
基于图3,利用光标定位法(时标法),可便捷地测量电路的时间常数。
依据图3(a)测量RC一阶电路充电(零状态响应)时间常数的步骤如下。
(1)移动光标2,读出电容C端电压UC的最大值和最小值,结果分别为2.6083V和0V。
(2)把光标1定位于电容C充电的起始处,即使x1=50.0000ms、y1≈0V;把光标2定位于电容C充电至稳态值(UC的最大值)的0.632倍处,即使x2=52.8743ms、y2=1.6484V。
(3)读取此时光标1与光标2之间的时间差dx,即为RC一阶电路充电(零状态响应)时间常数,τc=dx=2.8743m s。
参见图3(a),利用光标定位法,RC一阶电路放电(零输入响应)时间常数的测量结果为,τc=2.8756m s。
同样地,利用光标定位法,测量RL一阶电路充磁(零状态响应)时间常数的数据,如图3(b)所示,即x1=50.0000m s、y1≈0V,x2=53.1808m s、y2=270.5201m V,τL=dx=3.1808m s。
参见图3(b),RL一阶电路放磁(零输入响应)时间常数的测量结果为,τL=3.1838m s。
基于光标定位法,本文还依据图2的响应仿真结果,测量了电路的时间常数。RC一阶电路充、放电时间常数的测量结果分别为,τc=2.938m s和τc=2.931m s;RL一阶电路充、放磁时间常数的测量结果分别为,τL=3.178m s和τL=3.172m s。
由此可知,仿真测量的结果与理论值一致。
2.3 RC和RL一阶电路响应波形上升时间的仿真测量
在控制领域中,上升时间定义为响应曲线从稳态值的10%上升到稳态值的90%所需的时间。
利用光标定位法,依据图2,RC和RL一阶电路响应波形上升时间的测量结果分别为,trc=5.934m s和trl=6.742m s;而依据图3进行测量,则结果分别为,trc=6.2615m s和trl=6.9256m s。
3 RC和RL一阶电路响应的实验实现
3.1 RC和RL一阶电路响应实验
基于模拟电路实验箱(DICE-A9)上的电子元器件,以及荧光灯镇流器,依据图1(a)和图1(b),可便捷地搭建RC和RL一阶电路响应实验。
实验时,示波器(GDS-1102A-U)A通道探头使用×10档;信号发生器(AFG-2225)的参数设置为:方波,20Hz,10Vpp,占空比50%,偏置0Vdc(响应波形、时间常数与偏置设置无关)。利用固纬LCR-915测试仪,测量R、C、L元件参数。
参见图1(a),在RC一阶电路响应实验中,元件的测量值为:q=2.194kΩ,C=9.142μ F,3265Ω。据此计算,时间常数τC=ReqC=2.598m s;忽略Rq,则τC≈2.985m s。
李永林:新时代呼唤新担当,新时代需要新作为。肩负党和人民群众的重托,立足环渤海地区的宏大基业,面对打造世界一流能源化工企业的时代责任,天津石化正以时不我待、只争朝夕的紧迫感,全力融入京津冀协同发展,坚定不移做强做优做大国有资本,大力推进全产业链协同发展,加快建立创新引领、集约高效、智能融合、绿色低碳的先进工业体系。全力建成技术质量领先、配套设施完备、安全绿色环保、服务优质高效、集群效应凸显的世界级石化基地,成为向产业链高端攀升、向世界一流进军的杰出代表,成为拉动天津经济增长、助力人民美好生活的强劲引擎,推动美丽天津天更蓝、地更绿、水更清,环境更宜居、生态更美好、人民生活更加殷实安康。
利用华强牌荧光灯镇流器(参数:40W、220V、50Hz、0.43A、tw105、Δt55、λ0.5)作为电感元件(RL、L)。参见图1(b),在RL一阶电路响应实验中,元件的测量值为:q=2.194kΩ,L=59.32Ω,L=970.6m H,i=149.56Ω,。据此计算,时间常数τL=L/Req=3.204m s;忽略Rq,则τL≈ 3.160m s。
通过示波器观测到的RC和RL一阶电路响应的实验结果,如图4(a)、图4(b)所示。
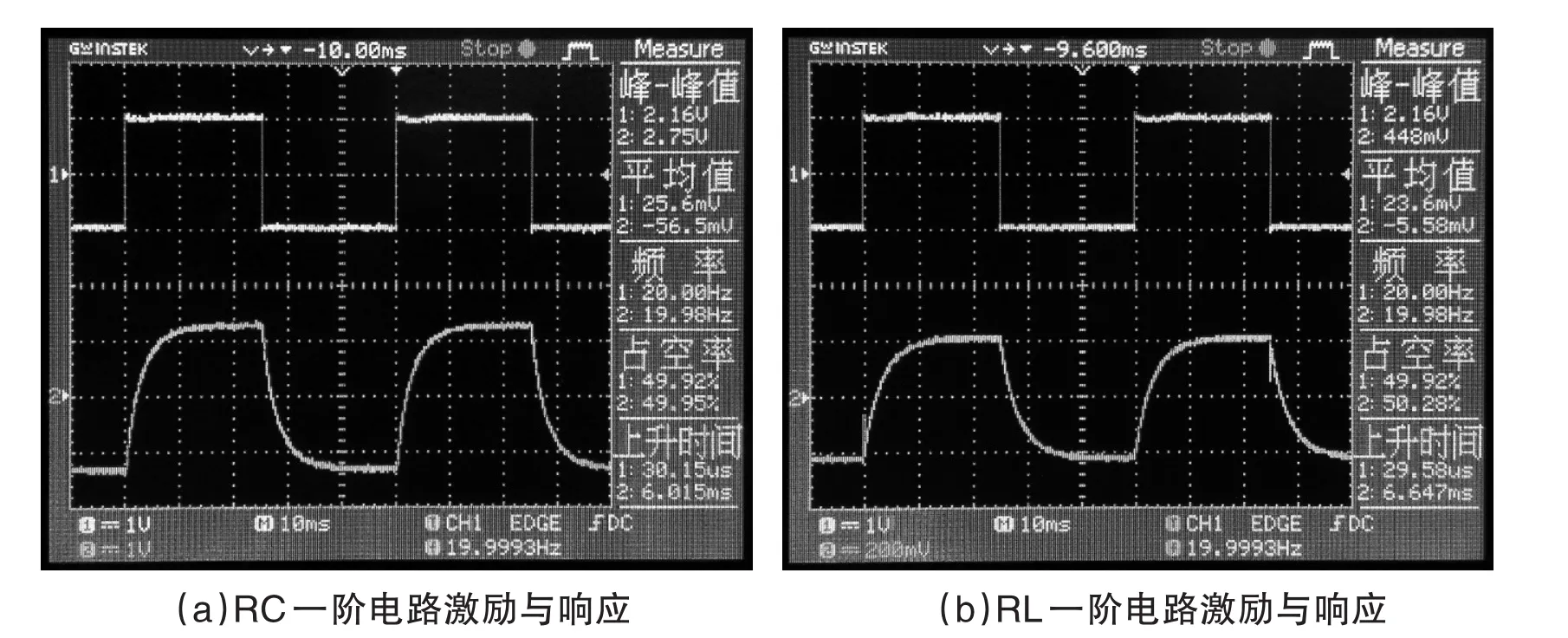
图4 RC和RL一阶电路响应实验结果
图4(a)中,通道1为激励方波,通道2为RC一阶电路响应波形。图4(b)中,通道1为激励方波,通道2为RL一阶电路响应波形。
比较图2与图4可知,实验结果与仿真结果一致。
3.2 RC和RL一阶电路时间常数的实验测量
3.2.1 依据上升时间测算电路的时间常数
对于图1(a)所示的RC一阶电路,依据仿真测量结果(平均值)可知,其上升时间与时间常数的关系为,trc=2.0982 τC。对于图1(b)所示的RL一阶电路,依据仿真测量结果(平均值)可知,其上升时间与时间常数的关系为,trl=2.1494 τL。
由于实验结果与仿真结果一致,并且实验元件的参数与仿真元件的参数相差细微,因此,可以依据实验结果响应波形的上升时间来测算电路的时间常数。
由图4(a)可知,RC一阶电路响应波形的上升时间为,trc=6.015m s,由此可测算出,τC≈2.867m s。由图4(b)可知,RL一阶电路响应波形的上升时间为,trl=6.647m s,由此可测算出,τL≈3.092m s。测算结果与理论值一致。
3.2.2 利用光标定位法测量电路的时间常数
实验示波器具有自动测量和光标测量功能。因此,基于实验示波器,利用光标定位法(时标法),同样可以测量RC和RL一阶电路的时间常数。
测量时,把通道1屏蔽,只显示并放大通道2的RC或RL一阶电路响应曲线。
依据图4的实验结果,RC一阶电路充、放电时间常数的测量结果分别为,τc≈2.740m s和τc≈2.760m s;RL一阶电路充、放磁时间常数的测量结果分别为,τL≈3.175m s和τL≈3.160m s。
实验测量结果,与仿真测量结果及理论值一致。
4 结论
本文利用NI Multisim14.0软件,仿真了RC和RL一阶电路的零输入响应及零状态响应,并利用光标定位法,测量了电路的时间常数。为了让学生深入理解动态电路响应及过渡过程,直观地比较仿真结果与实验结果,本文搭建了对应的实物实验,进行演示和测量。
依据仿真和实验的分析及测量结果可知:当方波的周期满足T/2≫5τ时,可用于模拟RC和RL一阶电路响应的正、负阶跃激励信号;通过仿真,可直观地观测RC和RL一阶电路响应的曲线及其动态过程,基于软件的瞬态分析等功能,利用光标法,可测量电路的时间常数;实物实验的结果,与仿真结果及理论值一致。
在RL一阶电路设计中,本文利用取样电阻来间接地观测电感电流,降低了实验成本。本文基于仿真结果,把时间常数与上升时间进行关联,通过类比,便捷地测算了实物实验电路的时间常数。
利用计算机仿真辅助RC和RL一阶电路响应教学,能让学生直观地观测到动态电路响应及过渡过程,从而深入理解其物理内涵及本质。利用本文的方法,可对二阶电路等动态电路进行仿真分析和实验研究。

