一种外骨骼负重重心波动调节机构设计与研究

(1.西南交通大学 先进驱动节能技术教育部工程研究中心， 四川 成都 610031；2.中北大学 信息与通信工程学院， 山西 太原 030051)

引言

外骨骼机器人是一种人体可穿戴的智能机电液一体化装备，其将参照人体尺寸设计的金属骨架与穿戴者肢体、背部贴合使用，使用过程中在保证人体的舒适性和运动灵活性的同时，增强穿戴者的身体机能。负重型下肢助力外骨骼的功能目标是增强穿戴者的负重能力，减少人体能量消耗、缓解疲劳[1]。当前该型外骨骼在各国军队已得到了广泛的应用，如美国HULC“浩克”外骨骼、XOS外骨骼，俄罗斯“勇士” 系列外骨骼以及法国提出的“大力神”外骨骼[2-5]。这些外骨骼的驱动器类型主要分为液压、气压、电机驱动，而液压驱动外骨骼系统以负重能力强的特点被广泛应用[6]。其中HULC“浩克”外骨骼较为典型，这种外骨骼是伯克利BLEEX外骨骼的加强版，HULC在BLEEX的基础上将单侧下肢驱动单元精简为髋关节，膝关节布置一套液压驱动缸[7]，这种动力配置也成为后来国内外众多外骨骼的常规选择。研究表明这些外骨骼可以有效支撑负重载荷，并将80%的负重传至地面，而人体自身只需承受20%的载荷。下肢助力外骨骼大大增强了穿戴者的身体机能，降低了人体的能量消耗，负重能力达到了40～90 kg[8-11]。

然而，当穿戴者带动外骨骼快速行走或跑步时，由于传感器延时等问题，施加在身体上的瞬时峰值载荷会显著增加，比静态载荷大2～3倍[12]。这是由于在人体行走时双腿交替屈伸使负重随着身体的重心在矢状面的垂直方向频繁的上升和下降造成的，具体表现形式就是日常人体在背着包行走时，背包会在身后上下摇摆。穿着外骨骼行走时负重重心在矢状面内也会有一个波浪形的运动轨迹，由此产生较大的峰值载荷使得在大负荷的情况下很难高速移动，并且也可能导致穿戴者的肌肉和骨骼遭受峰值载荷的冲击损伤。此外，随着运动时间的增加，人体的代谢率也会大幅增加，于是在外骨骼的髋部和背部设计了一种连杆绳轮机构来解决上述问题，以下简称髋背机构。

装备髋背机构后的系统重心运动轨迹是由下肢的行走运动和连杆绳轮机构的运动共同造成的，所以在运动学理论分析时先对未装备髋背机构时的重心轨迹进行求解，再对连杆绳轮机构进行分析。

1 未装备髋背机构的重心轨迹

1.1 步态分析

研究人体行走过程中负载在矢状面内的重心位置变化，需要分析人在正常行走过程中的步态参数。图1为一个完整的人体步态周期，人体在行走过程中，双腿对体重进行交替支撑，所以在一个步态周期内存在一个下肢承受体重的时期称为支撑相，一个下肢自由摆动的时期称为摆动相，支撑相占步态周期的60%，摆动相为40%。人体在行走过程中躯干重心之所以在矢状面内会有一个波浪形的起伏运动，是由于在行走过程中左右腿的髋关节、膝关节，踝关节分别在支撑相和摆动相期间不同的屈伸状态造成的。

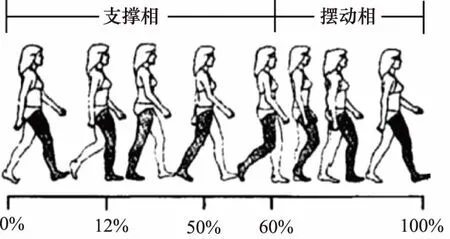
图1 人体步态周期

文献[13-14]提供了人体各体段重量与总体重、人体各体段长度与总身高的关系，如表1所示。人体的行走过程是由双腿各个关节处的肌肉发力带动腿骨完成的，排除非正常因素，可以认为正常人体在平直地面上的行走运动是周期、重复的，下肢的各个关节分别在每一个步态周期内具有同样的角度变化函数，文献[15-17]给出了行走状态下关节运动临床分析测试数据(CGA)，CGA包括不同体型人体在相同试验条件下一个步态周期内左右腿的髋关节、膝关节、踝关节角度变化曲线。根据CGA曲线中取得的关键数据点拟合出下肢各关节的角度驱动函数用于运动学建模。

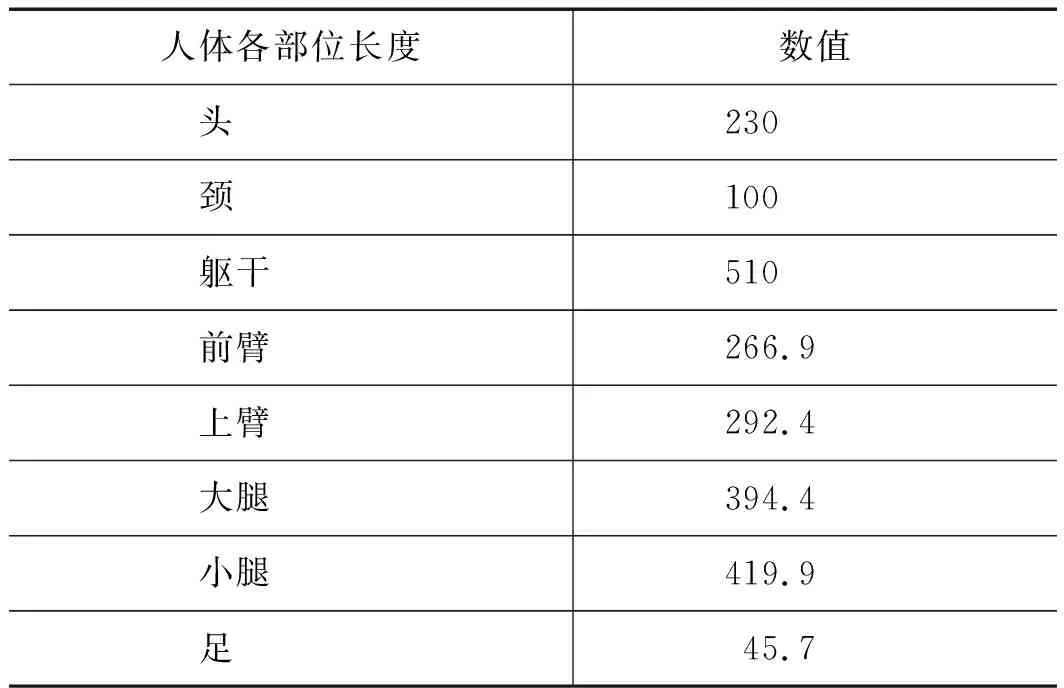
表1 人体各肢体长度 mm

在外骨骼运动分析中，下肢和躯干可以看作为一个七杆机器人系统，而在研究人体重心在矢状面内的运动时可单独把躯干和一侧下肢的大腿、小腿、足4个体段看作4个串联的杆件，运用机器人运动学方法，在已知下肢各体段长度以及各关节轴的角度驱动函数之后便可以得出人体重心在矢状面内的运动轨迹。

1.2 运动学建模

人体行走时重心轨迹的运动学建模就是建立人体躯干通过大腿、小腿到足的空间位置关系，确定下肢各关节的角度变化信息后利用Denavit-Hartenberg方法求解运动学正解，得出足尖的轨迹，再以足尖为定点便可得出人体重心及负重重心的轨迹。按照D-H方法，在每个连杆上建立坐标系，利用刚体位姿转换矩阵求出连杆在基础坐标系中的位姿。2个相连刚体之间的转换矩阵分为4步：

(1)

式中, c为余弦运算(cos)； s为正弦运算(sin)。

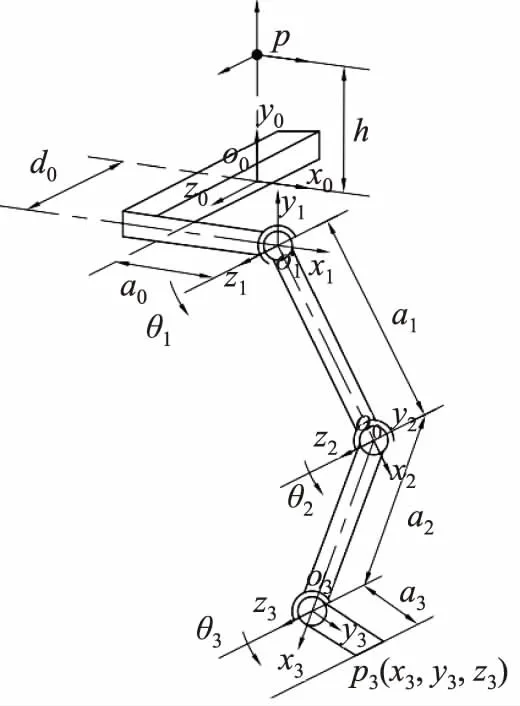
图2 D-H坐标系

如图2所示，建立右下肢各连杆的D-H坐标系，为方便计算原点o0放在负载重心下方的腰部后方中心位置，z轴沿冠状轴，x轴沿水平方向，y轴沿铅垂方向。负重重心p与o0点的距离为h。下肢各肢体连杆的原点o1，o2，o3放在关节轴线与相邻关节公垂线的交点位置，z1，z2，z3轴沿关节轴线方向，x1，x2，x3轴与公垂线共线，y1，y2，y3轴是分别由各自x，z轴右手定则确定。θ1，θ2，θ3分别表示髋关节、膝关节和踝关节在D-H坐标系中的转角，其中膝关节θ2、踝关节θ3角度与CGA相应的关节转角定义一致，θ1与CGA数据中髋关节转角θhip的关系为:

(2)

其中，a0，a1，a2，a3分别表示腰后部中心、髋关节轴线、膝关节轴线、踝关节轴线、足尖的距离，这样便可得出D-H坐标系的参数，如表2所示。

表2 D-H参数表

根据以上提供的参数，相邻两杆的转换矩阵可以给出：

(3)

(4)

(5)

(6)

将t1,t2,t3,t4相乘便可得到足尖相对与o0坐标系的变换矩阵：

(7)

式中, c1+2+3指cos(θ1+θ2+θ3)，其余同理。

则足尖在o0坐标系内y轴上的轨迹为:

yf=a3sin(θ1+θ2+θ3)+a2sin(θ1+θ2)+a1sinθ1

(8)

以足尖为定点求重心p点的y轴方向的轨迹为:

yp=yf+h

(9)

因为关节转角θ是关于步态周期时间t的函数，人体在行走过程中左右腿交替承重，左右腿的支撑时间各占50%。所以一个步态周期内，负重重心的轨迹分为左腿支撑段和右腿支撑段，图3为D-H方法计算的未装备髋背机构的y方向负重重心轨迹。

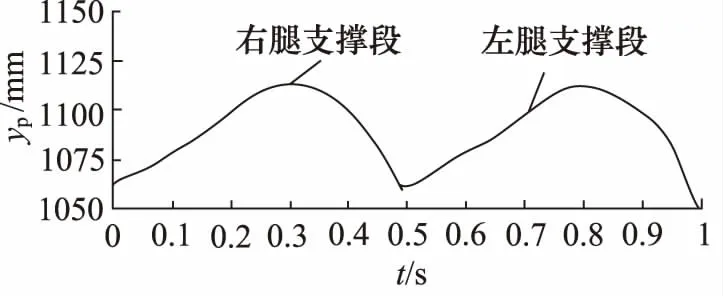
图3 未装备髋背机构的y方向负重重心轨迹

2 髋背机构

髋背机构采用连杆机构直接将外骨骼大腿部分的运动传动至负重托架。相较传感器信号驱动，其具有零延时优点。髋背机构由机架、传动连杆、负重托架组成，其中负重托架与机架之间，传动连杆和机架之间采用滑动导轨联接；负重托架与传动连杆采用柔性绳和定滑轮联接，如图4所示。人体在平直地面传动连杆由外骨骼的大腿部提供动力，通过柔性绳和定滑轮传动至负载托架，驱动负重与人体重心在矢状面y轴方向上内做相反的运动，从而达到减少重心垂直位移的目的。

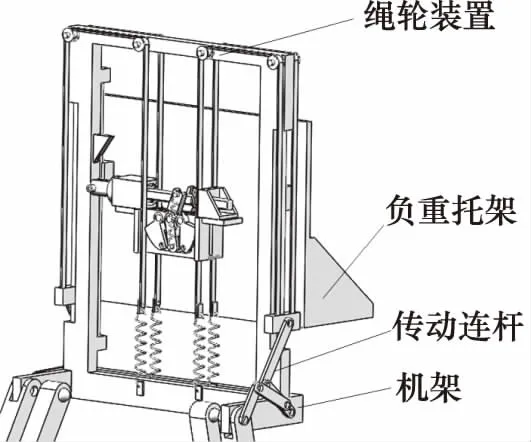
图4 髋背机构

2.1 髋背机构原理

如图5所示连杆传动机构为六连杆及定滑轮机构，AD为髋背机架，铰点D同时也是外骨骼髋关节，连架杆CD与外骨骼的大腿部固连，即CD杆的转动角度、方向与髋关节转动角度、方向相同。

此六杆机构可分解为1个铰链四杆机构ABCD和1个曲柄滑块机构AEF， 其中铰链四杆ABCD的功能是传递髋关节的角度变化信息，从前面的步态分析可以得到，当髋关节转动角度相对躯干为6.57°时，人体重心的垂直高度也达到了最高点，当髋关节前伸和后屈分别达到极限位置时，躯干重心的垂直高度到达最低点。针对这种特点，引入曲柄滑块机构的3个运动状态分别与髋关节前伸后屈的3个状态相对应。即AEF-DC，AEF′-DC′，AE″F″-DC″。

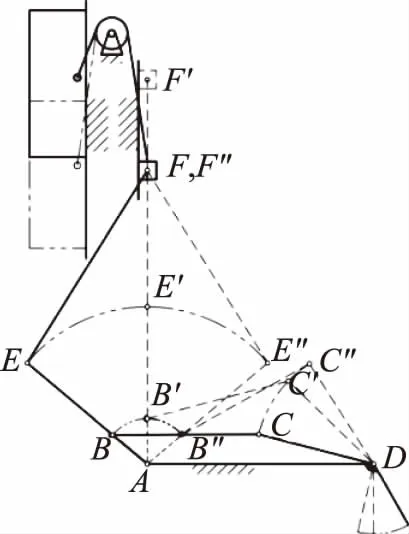
图5 髋背机构原理图

对于铰链四杆ABCD即为已知CD连架杆和AB连架杆的3个位置，考虑到整个髋背机架的尺寸，连杆的设计不能干涉到人的肢体活动如手臂的摆动，AE杆长度受到限制，所以曲柄AE杆的摆动角度取在设计时应取较大值，在设计铰链四杆ABCD时连架杆CD的转角范围约为43°，还应考虑髋关节的转角曲线0°线左右两边不是左右对称的，故铰链四杆不能采用平行连杆，且连架杆AE的设计摆动角度大于43°，故AB长应取短，则取杆长lAB为20 mm。

由图3可知负重重心的位移范围为40.11 mm，取EF杆长lEF为100 mm，根据曲柄滑块机构的滑块位移公式列出方程组:

(10)

求得曲柄杆长r=lAE=69.29 mm。

现已知在铰链四杆ABCD中连架杆AB的3个位置以及对应的连架杆CD的3个角度位置，便可利用反转法求出连架杆上C点的位置，如图6所示。

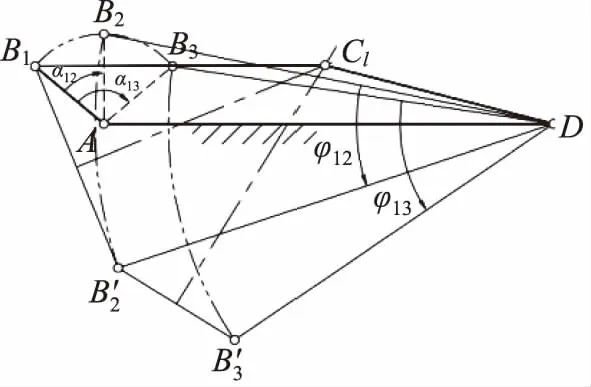
图6 反转法求解连杆

求得铰链四杆的四杆长度分别为：lAB=20 mm，lBC=100.7 mm，lCD=41.3 mm，lAD=100 mm。

2.2 装备髋背机构后的重心轨迹

通过反转法得出连杆机构的杆长之后，便可确定2个连架杆摆角之间的关系，即β1=f(β3)，β3就是D-H方法中的髋关节转角θ1。建立坐标系Oxy如图7所示，把各连杆对坐标轴进行投影可得方程式(11)：

(11)

式(11)可简化为：

cos(β1+α1)=Q0cos(β3+φ3)+Q1cos(β3+

φ3-β1-α1)+Q2

(12)

其中,Q0=c/a，Q1=-c/d，Q2=(a2+d2+c2-b2)/2ad。

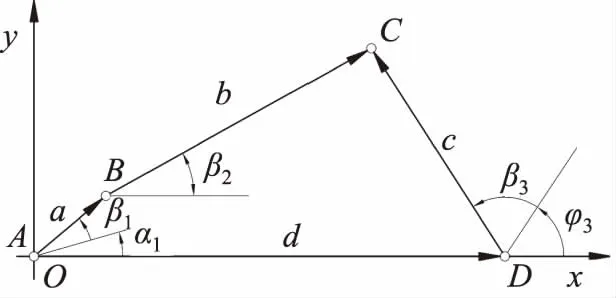
图7 按连架杆对应位置求θ1， θ3关系

式(12)为隐函数，有关β1关于β3的表达式不能直接求出，已知髋关节的角度驱动函数曲线后，即β3已知。使用MATLAB的fsolve命令求解式(12)可以相应地得出连架杆AB的角度变化曲线。即为曲柄AE角度函数已知，由式(9)和式(10)以及定滑轮改变运动方向的特点，可得出D-H方法下负重在矢状面内的垂直位移曲线。

2.3 ADAMS仿真结果

由于装备髋背机构的外骨骼系统机构比较复杂，所以前面的理论分析中分别单独对下肢行走运动和髋背机构的原理进行分析，再将二者通过运动合成得到装备髋背机构之后的重心轨迹。

ADAMS具有很强大的多刚体系统的运动学及动力学仿真能力，可以建立人体和外骨骼联合模型直接求解出装备髋背机构之后负重重心的轨迹。由表1在Solidworks中建立模型导入ADAMS，如图8所示，根据CGA曲线在各个关节处添加驱动函数、驱动模型进行仿真运算，理论计算和仿真结果如图9所示。

图8 ADAMS中的仿真模型

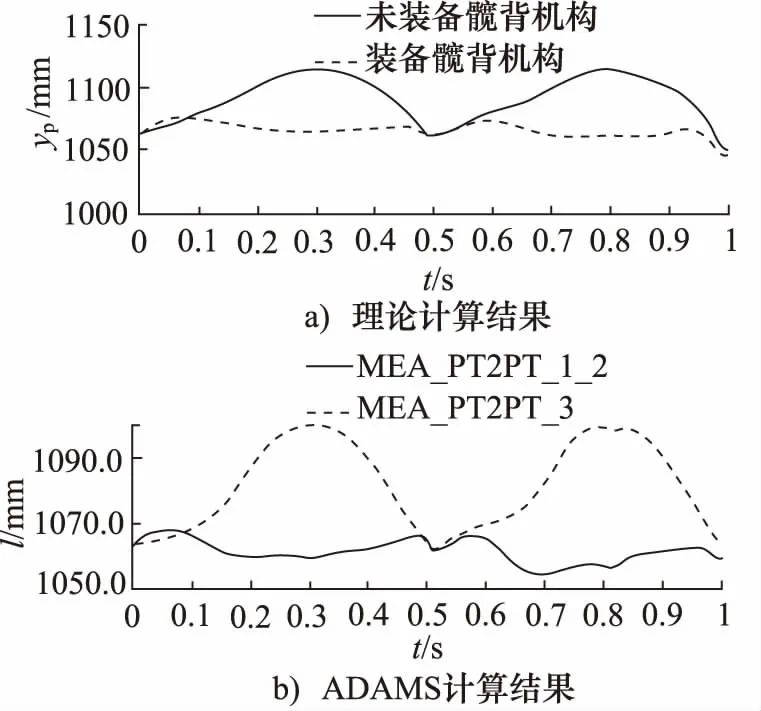
图9 装备髋背机构的y方向负重重心轨迹

3 结论

(1) 基于穿戴外骨骼时人体的步态特性，在理论上第一步用坐标变换和D-H方法建立外骨骼下肢运动学模型，先获得了未装备髋背机构时重心的轨迹；第二步利用连杆设计理论通过六杆机构将髋关节的旋转运动转化为负重相应的上下平移运动，求解运动学方程得到了装备髋背机构后的重心轨迹；

使用ADAMS的运动学仿真功能把理论计算的2个步骤整合为1个装备有髋背机构的外骨骼仿真模型，通过理论计算结果和仿真结果进行对比，验证了D-H方法和连杆设计理论在髋背机构设计中的正确性；

(2) 由D-H方法和连杆设计理论方程求解和ADAMS仿真结果可以看到：不装备髋背机构时负重重心在矢状面y轴方向上下波动约为40 mm，装备髋背机构之后减小至约8 mm，证明了髋背机构减小负重重心轨迹波动的有效性。