基于数据挖掘方法的物流业景气信号灯模型构建

陈东清 黄章树

(1. 福州大学至诚学院， 福建福州 350002 ; 2. 福州大学经济与管理学院， 福建福州 350108)

一、引言

物流产业是支撑经济结构调整、推动经济增长方式转变、提高经济运行质量的重要引擎，在新一轮全球经济发展形势下，现代物流发展水平已经成为评价国家全球经济竞争力的重要指标。准确把握物流产业发展态势，掌握物流市场景气状况，可为政府宏观调控及企业生产经营管理提供决策数据支持。

由于经济发展存在周期性波动规律，许多学者尝试用经济景气指数刻画经济系统运行规律，并在经济景气指数的预测及预警方面开展研究工作。李学文等考虑消费、政策、生产要素等多方面因素，建立了较为全面的指标体系，测算湖南省宏观经济景气预警指数，并通过与GDP的增速对比，发现所构建的景气指数能够较好反映经济走势[1]；周德全综合运用Delphi法、K-L信息量法、经验借鉴法建立中国干散货海运景气指标体系，并构建预警模型，发现我国近期的干散货海运市场环境存在偏冷风险[2]；李佳璐等设计了上海市海洋经济的预警信号系统，采用数理统计方法确定预警区间的临界值，同时认为由于产业经济形态的差异性，预警区间的临界值选择标准也会存在差异[3]；解钰茜等根据正态分布原理采用 3σ法，借助信号灯方法研究经济系统与环境承载压力之间的关系，预警效果显著[4]；隋新玉借助新型经济指数研究分析我国经济景气状况，采用的是经济理论、国际惯例、人工经验相结合的方法确定预警模型临界点[5]；刘春涛等运用赋值方法得到沈阳市旅游产业历年各指标的警情分值，利用加权平均法计算综合预警指数得分，以3σ方法为标准划分预警线，分析旅游业发展趋势。[6]

关于经济景气指数信号灯模型的研究较为丰富，但还存在以下不足：(1)现有研究主要采用3σ原理划分预警区间，但是不同地区的经济发展水平、产业经济形态存在较大差异，选择偏离几倍标准差作为异常区间是个难题，如果选择偏离3σ可能导致异常的样本较少，预警意义不大，如果选择偏离1σ之外作为异常区间，异常的样本可能较多，也失去预警价值；(2)部分学者采用人工经验划分预警区间，存在较强的主观性，影响预警模型的精度。因此，本文引入数据挖掘方法构建物流业景气信号灯模型，采用K均值聚类分析方法对物流业景气指数进行聚类分析，综合考虑轮廓系数均值及各个样本的轮廓系数值选择合适的聚类数量，将物流业景气指数归为不同类别，再运用C5.0算法构建决策树，得到不同类别的判定规则，将该判定规则作为物流业景气信号灯模型的预警区间，最后以福建省物流业景气指数信号灯模型的构建作为实证研究，验证模型的有效性。

二、聚类方法和决策树方法选择

(一)K均值聚类方法

聚类分析是常用的数据挖掘方法，可方便识别不同数据的特征、特定分布及模式，在客户细分、市场细分、模式识别、图像处理、生物医药等不同领域得到广泛应用。K均值算法是聚类分析理论常用的算法，主要计算思路：从所有样本中随机选取K个点作为初始聚类中心，根据距离公式计算每个样本到初始类中心的距离，以样本到聚类中心距离最小为原则进行聚类，直到所有样本归类结束。以误差平方和准则函数的收敛性作为迭代结束的判断依据，主要计算步骤如下[7]：

(1)假设样本集为Xi(n)，令M=1，采用随机方法初始化K个聚类中心，第M个聚类中心可记为Cj(M),j=1,2,3,…,k。

(2)选择距离公式，计算每个样本与聚类中心的距离：

D(xi,Zj(M))

(i=1,2,3,…,n,j=1,2,3,…,k)

(1)

如果D(xi,Zj(M))=min{D(xi,Zj(M))},i=1,2,3,…,n,则Xi∈wk。

(3)计算误差平方和准则函数JC：

(2)

针对聚类结果有效性的判断方法较多，常见的判断指标有凝聚度、分离度、距离评价函数、轮廓系数，而轮廓系数综合考虑凝聚度和分离度，因此本文选择轮廓系数评价聚类结果的有效性。记第i个样本到所属类所有样本的平均距离为ai，计算第i个样本到给定类(不包含该样本的所属类)所有样本的平均距离，最小值记为bi，记第i个样本的轮廓系数计算公式为：

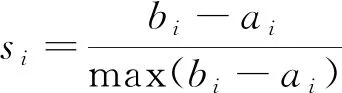
(3)

通过上述公式可知，轮廓系数取值范围为[-1,1]，当轮廓系数=1，代表该样本与其他类的差异性大；当轮廓系数=0，代表该样本划分不明显；当轮廓系数=-1，代表该样本被错误划分到某个类，还有更优的聚类方案。

对于聚类个数为K时，平均轮廓系数为[8]：

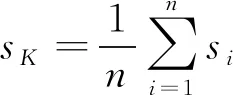
(4)

综上分析，单个样本的轮廓系数衡量该样本聚类结果的合理性，一般认为单个样本的轮廓系数大于0.2，代表该样本划分结果较合理；平均轮廓系数评价总体聚类模型的有效性，选择合适的聚类个数需要综合考虑总体平均轮廓系数及单个样本的轮廓系数。

(二)C5.0决策树方法

决策树是一种从复杂、无规则的事例中推理判别规则，并应用于数据分类预测的非参数方法，该方法不用事先设定函数关系式，模型推理结果直观，特别适用于交通、医学、经济管理等复杂的大数据集分类预测领域。常用的决策树算法有回归分类树、CHAID、QUEST、ID3、C4.5、C5.0等。C5.0是ID3的改进算法，在执行效率方面具有较大优势，C5.0算法以信息熵下降速度作为确定最佳分组变量和最佳分割点依据。[9]

记信息ui(i=1,2,3，…,r)的发生概率Pi(ui)构成信息源模型，∑Pi(ui)=1(i=1,2,3,…,r)。信息量是以2为底的对数形式(单位:bit)，其数学定义为[10]：

(5)

信息熵是信息量的数学期望值，定义为：

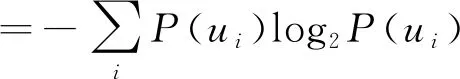
(6)

设数据集合S，目标变量C有K个分类，F(Ci,S)表示S中属于Ci类的样本个数，|S|表示数据集合S的样本个数，根据上述信息熵的定义，集合S的信息熵可表示为：

(7)

对于某属性变量T，有n个分类，则属性T引入后的条件熵可表示为：

(8)

属性变量T引起的信息增益表示为：

Gain(T)=E(S)-E(T)

(9)

通过上述公式计算信息增益，得到最佳的分组变量和分割点，重复上述步骤，构建多分枝的决策树。

三、物流业景气信号灯模型构建

(一)物流业景气指数

为了监测我国物流行业的发展趋势，中国物流与采购联合会协同相关部门科学设计指标体系，广泛采集行业数据，综合测算物流业景气指数。中国物流业景气指数(LPI)于2013年3月5日由中国物流与采购联合会、中国物流信息中心正式对外发布，该指数体系包含业务总量、新订单、从业人员、库存周转次数、设备利用率、平均库存量、资金周转率、主营业务成本、主营业务利润、物流服务价格、固定资产投资完成额、业务活动预期12个分项指数,由业务总量、新订单、从业人员、库存周转次数、设备利用率5个指标加权计算得到。[11]

随着中国物流业景气指数的发布，福建、浙江、江西、山西、甘肃、河南、安徽等省份也陆续发布了区域性的物流业景气指数，丰富了我国物流业景气指数的内涵，为监测区域性物流行业发展态势提供了可靠的数据支撑。

(二)基于数据挖掘方法的信号灯模型构建

本文借鉴跨行业数据挖掘标准流程(CRISP-DM, cross-industry standard process for data mining)思想，提出了物流业景气信号灯模型构建方法，如图1所示，主要包含以下几个步骤：

(1)数据采集及预处理。采集物流业景气指数数据，如果数据中存在空缺值、异常值等，需要对数据进行清洗，确保分析数据的完整性和可靠性。

(2)构建、优选K均值模型。将所有样本作为K均值的建模样本，聚类数量选择为2到n(n最大值一般取10)，构建不同的K均值模型，计算每个样本的轮廓技术及不同聚类模型的平均轮廓系数，综合考虑样本的轮廓系数及平均轮廓系数，确定最优的聚类数量，以最优聚类数量所对应模型计算样本的所属类。

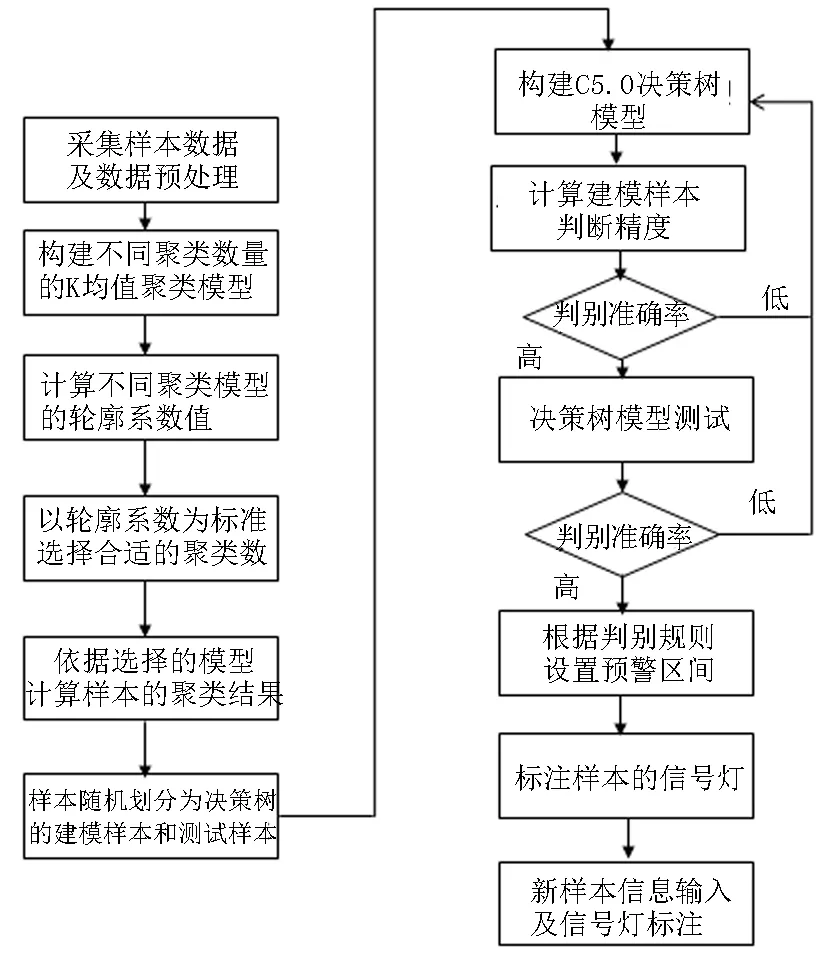
图1 基于K均值聚类和C5.0决策树的物流业景气信号灯模型构建步骤

(3)构建C5.0决策树模型。随机将所有样本划分为建模样本和测试样本，利用建模样本构建C5.0决策树模型，并计算建模样本的判别准确率，如果较高则利用测试样本再次检验模型的测试精度，测试精度满意的条件下，进入第(4)步骤；如果决策树的建模精度或者测试精度较低，则重新调整C5.0相关参数，直到获得满意的模型结果。

(4)划分预警区间。根据所构建C5.0决策树的判别规则作为物流业景气指数的预警区间。

(5)标注信号灯。根据预警区间，给予不同预警区间的经济含义，标注样本的信号灯，实现数据可视化。

(6)新样本的信号灯标注。对于未来时间的物流业景气指数，根据上述设置的预警区间，判定景气信号，标注信号灯。

四、福建省物流业景气信号实证分析

(一)数据来源

福建省物流业景气指数由福建省工业和信息化厅、福建省物流协会联合发布，并在福建省经济信息中心网站公开发布。本文从该网站整理所需的月度数据，统计区间为2014年4月至2019年7月，具体数据见表1。

表1 2014年4月-2019年7月福建省物流业景气指数

数据来源：福建省经济信息中心网站

(二)物流业景气指数聚类结果分析

借助MATLAB 7.9.0工具编程实现上文介绍的K均值聚类模型，并对福建省物流业景气指数进行聚类分析。聚类模型的最大迭代次数设置为10000，距离函数设置为平方欧氏距离，聚类数量最小值为2，最大值为10，整理不同聚类数量K均值模型的轮廓系数值，并统计整理如表2所示。

表2 不同聚类模型的轮廓系数统计结果

从表2可以看出聚类数量为2时，轮廓系数平均值最大，但是有1个样本的轮廓系数小于0；聚类数量为10时，轮廓系数平均值排序第二，但是有1个样本的轮廓系数小于0.2；聚类数量为6时，轮廓系数小于0.2的样本个数均为0，轮廓系数平均值排序为第三。从图2的轮廓系数图也可以看出，大部分样本的轮廓系数值都较大，综合考虑，选择聚类数量为6。

聚类结果的标签是一个无序分类变量，为了方便识别，对聚类标签进行变换处理，聚类标签数值越大，物流景气度越高。整理得到各个类平均值及样本个数分布情况如表3所示。

图2 聚类数量为6的轮廓系数值

表3 不同类的均值及样本个数

(三)C5.0决策树结果分析

以福建省物流业景气指数作为输入，K均值聚类结果作为输出，采用Clementine 12.0的C5.0决策树算法构建决策树模型。将样本随机划分为两部分，其中59个作为建模样本，5个作为测试样本，具体的建模及测试流程如图3所示。对样本随机划分5次，发现建模阶段、测试阶段模型的判别准确率都达到100%，说明所构建的决策树模型稳健性良好。

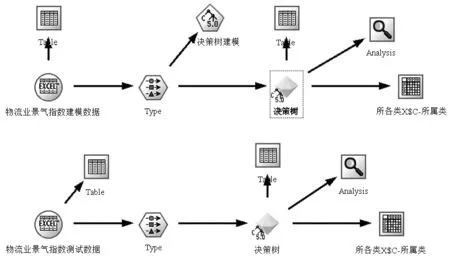
图3 决策树建模及测试流程

根据决策树的判定规则建立物流业景气指数的信号灯系统，如表4所示。该信号灯系统将福建省物流业景气度划分为“过冷”“趋冷”“正常区域下轨运行”“正常区域上轨运行”“趋热”“过热”六种状态，并依次用“蓝灯”“浅蓝灯”“绿蓝灯”“绿黄灯”“黄灯”“红灯”六种信号灯标识。

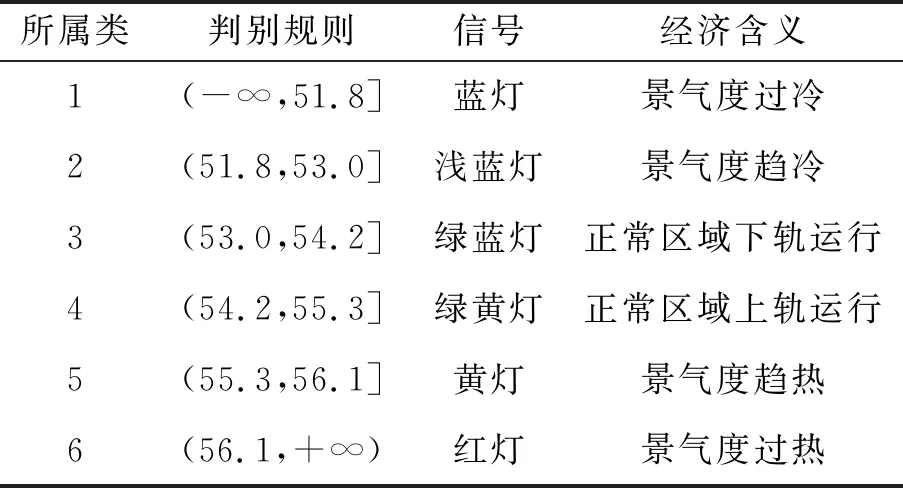
表4 福建省物流业景气指数信号灯系统

(四)信号灯模型结果分析

根据信号灯系统标识福建省物流业景气信号灯如图4所示。从图4可以看出，福建省物流业景气度变化可归纳为三个阶段：从2014年4月到2016年2月，福建省物流业景气度从趋热状态逐渐转变为过冷状态；从2016年3月到2018年12月，福建省物流业景气度从过冷状态逐渐转变为过热状态；2019年1月到2019年7月，福建省物流业景气度基本稳定处于趋热状态。

总体而言，大部分月份福建省物流业发展较为正常(非过冷或者过热)，45.31%的月份处于正常区域上轨或者下轨平稳运行，84.38%的月份处于趋冷到趋热区间运行，只有4.69%的月份处于趋冷状态运行，10.04%的月份处于趋热状态运行。由于受到春节因素影响，2015年2月、2016年2月物流业景气度处于过冷状态，受到台风、高温天气影响，2015年8月物流业景气度也处于过冷状态。从2018年3月到2019年7月，福建省物流业景气度都处于趋热以上状态，并且有3个月份存在过热的风险。从现阶段的宏观经济环境看，我国经济从高速发展转向高质量增长，物流业难以持续大幅度高速粗放增长。确保物流业与经济协调发展是一个关注的焦点，上述现象应引起足够的重视。

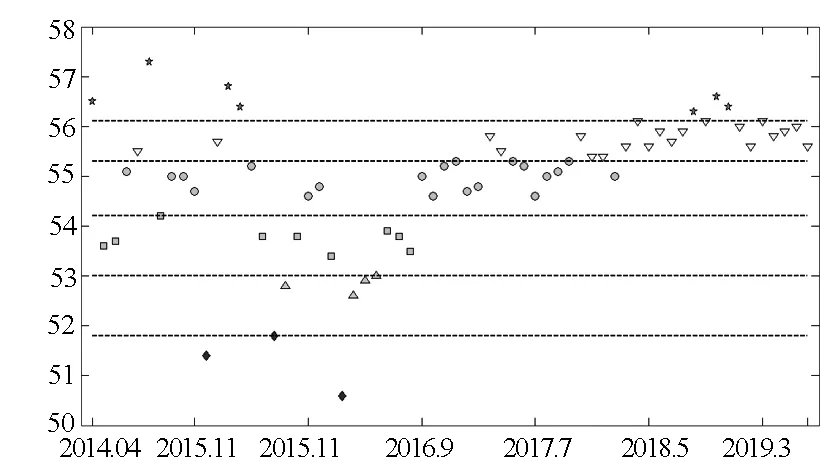
注: ◆过冷▲趋冷■正常负偏离●正常正偏离▼趋热★过热图4 基于数据挖掘算法的福建省物流业景气信号灯

五、结论

本文提出了基于K均值聚类和C5.0决策树相结合的物流业景气指数信号灯模型，通过实证研究表明，大部分月份福建省物流业发展较为正常(非过冷或者过热)，但是从2018年3月到2019年7月，福建省物流业景气度全部处于趋热以上状态，并且有3个月份存在过热的风险。

该模型解决了传统以3σ原理划分预警区间时，选择几倍标准差作为预警区间的难题，从实证结果来看，模型具有良好的监测示警作用。根据福建省经济信息中心网站发布的数据，2019年8月福建省物流业景气指数为55.9，由表5中的预警区间可以判断，2019年8月福建省物流业景气度处在趋热状态。由于受限于统计数据的原因，在一定程度上影响了模型的精度，在后续研究中可扩大物流业景气指数的样本量，进一步验证模型的有效性和稳健性。

注释：

[1] 李学文、李明贤：《湖南省宏观经济景气预警指数的构》，《系统工程》2015年第12期。

[2] 周德全、真 虹：《中国干散货海运景气监测及预警指标与模型研究》，《交通运输系统工程与信息》2017年第5期。

[3] 李佳璐、胡 昊、贾大山：《上海市海洋经济景气预警实证研究》，《上海管理科学》2015年第4期。

[4] 解钰茜、吴 昊、崔 丹,等：《基于景气指数法的中国环境承载力预警》，《中国环境科学》2019年第1期。

[5] 隋新玉：《基于新型经济指数对我国宏观经济景气状况的研究》，《价格理论与实践》2018年第3期。

[6] 刘春涛、刘馨阳：《沈阳市旅游产业景气指数测度及预警研究》，《国土与自然资源研究》2019年第4期。

[7] 吴文静、景 鹏、贾洪飞,等：《基于K均值聚类与随机森林算法的居民低碳出行意向数据挖掘》，《华南理工大学学报》(自然科学版)2019年第3期。

[8] 舒 浩、陈盛双、李石君：《基于最优k均值聚类的时空动态背景模型》，《小型微型计算机系统》2019年第2期。

[9] 王茂光、葛蕾蕾、赵江平：《基于C5.0算法的小额网贷平台的风险监控研究》，《中国管理科学》2016年第S1期。

[10] 张 宇、张之明：《一种基于 C5.0决策树的客户流失预测模型研究》，《统计与信息论坛》2015年第1期。

[11] 刘晓梅：《中国物流业景气指数的趋势周期分解及其经济含义》，《商业经济研究》2016年第11期。