基于基因表达式编程的计算机组卷算法研究

韩 啸，毕 波，唐锦萍

(1.东北石油大学 数学与统计学院，黑龙江 大庆 163000;2.黑龙江大学 数据科学与技术学院，黑龙江 哈尔滨 150080)

0 引 言

随着当代教育技术及科学技术的迅速发展，传统的教学与考试方式已渐渐无法适应现代化的教学要求，因此网络化的教学考试已渐渐步入人们的视野。网络化的教学考试的关键在于能够快速智能地组成试卷，即在计算机上设置试题库，并通过适当的算法挑选出试题并构成试卷，这类算法相较于传统的人工组卷来说更为高效[1]。

通过网络化的考试模式，不仅可以减轻教师及学校的工作量，而且更能激发学生的学习热情、提高学生的学习效率。

目前的在线考试系统已经可以实现智能组卷、在线答题、在线阅卷等一系列功能。但由于一些现实条件的约束，各类在线考试系统在智能组卷方面还不够成熟；大批量产生试卷时速度慢、质量差是现阶段组卷算法的主要缺点。

针对现阶段在线考试系统组卷速度慢、质量差、题型不均衡等不合理的问题[2]，文中首先给出了组卷问题的数学模型，将组卷问题归结为一个约束非线性优化问题，并提出了基于基因表达式编程的自动组卷算法，将该算法用于求解组卷优化问题，实验证明该算法有着较高的计算效率和良好的实用性。

1 常见智能组卷算法

常见的智能组卷算法包括以下4种：

(1)基于随机算法的组卷算法。

随机组卷算法是依据已经确定的试卷标准进行随机抽取试题[3]，在组卷时，利用二项分布函数建立数学模型，按照试题的类型、试题的难度、知识点等约束条件进行选择。

该算法结构简单、易于理解，常常应用于容量较小的试题库组卷系统中[4]。当系统中试题过多时，组卷的时间会变长且成功率低。

(2)基于回溯算法的组卷算法。

回溯算法实际上是一个类似于枚举的搜索尝试过程[5]，是一种选优搜索的方法，按选优条件向前搜索以达到目标,在搜索尝试的过程中寻找问题的解，当不满足求解条件时就进行“回溯”[6]，尝试别的路径，重新抽取试题。

在试题种类少、数量少的情况下，回溯算法优于随机算法[7]。但当试题种类增多、试题量增加后，使用回溯算法生成试卷的速度明显变慢[8]，且选取的试题不能保证是最优的，所以在智能组卷中回溯算法很少被使用。

(3)基于遗传算法的组卷算法。

遗传算法(genetic algorithm，GA)是一类借鉴生物界的“适者生存，优胜劣汰”的遗传机制演化而来的随机化搜索方法[9]。该算法采用简单的编码技术对试题库中的试题进行编码，生成初始的种群。然后通过复制、交换、突变三种操作产生下一代新的种群。并且一代一代朝向适应度函数的方向发展，直至产生满足出卷要求的试卷。

遗传算法在智能组卷中是比较灵活的方法，适用于具有多约束条件的组卷问题[10]。但在组卷过程中由于试题量的增加，“早熟”的问题逐渐显现出来，所以如何提高算法执行效率，解决“早熟”问题成为了重要的研究问题。

(4)基于粒子群优化算法的组卷算法。

粒子群优化算法是模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法[11]。粒子群算法首先从试题库中随机抽取若干套试卷，构成最初的粒子群(每个粒子代表一套试卷)。然后，运用适应度函数计算每个粒子的值，判断其是否符合要求。如果不符合继续迭代，直至选取到符合要求的试卷。

粒子优化种群算法在计算大规模试题库系统时编码简单，搜索速度更快，效率更高，但是不适宜处理离散的优化问题，且在选择遗传算子时比较麻烦。

2 组卷问题的数学模型

组卷是指从一个试题库中在满足给定规则的情况下，根据确定的参数及算法，从试题库中筛选组合出一套满足要求的、科学的、合理的试卷。

进行组卷时需要给定以下的约束条件：试题数量、总分、题型个数、题型分数等。首先用xn来表示题型，用yn来表示章节，ki=1表示选择某题，ki=0表示不选择某题，如表1所示。

表1 试卷的约束条件

根据表1，可列出约束条件：

①试题数量约束。

(1)

②总分约束。

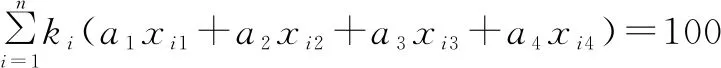
(2)

式(2)表示试卷总分为100分。

③题型个数约束。

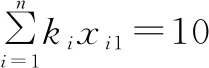
(3)

(4)

(5)

(6)

式(3)表示被选中的试题中选择题的个数为10个，式(4)表示被选中的试题中填空题的个数为10个，式(5)表示被选中的试题中判断题的个数为10个，式(6)表示被选中的试题中大题的个数为4个。

④每章所有题型的总分约束。

(7)

(8)

(9)

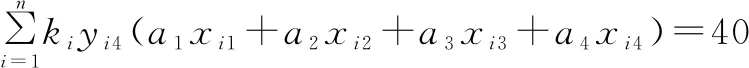
(10)

其中，yim表示第i题在第m章，

式(7)表示第一章被选中的所有试题的总分，第一章试题占20分。式(8)表示第二章被选中的所有试题的总分，第二章试题占20分。式(9)表示第三章被选中的所有试题的总分，第三章试题占20分。式(10)表示第四章被选中的所有试题的总分，第四章试题占40分。

⑤某章必有某种数量题型约束。

(11)

(12)

(13)

式(11)表示第一章被选中的题必须包含1个大题，式(12)表示第二章选中的题必须包含2个选择题，式(13)表示第三章选中的题必须包含1个判断题。

3 基因表达式编程算法在组卷算法中的应用

3.1 基因表达式编程算法的介绍

基因表达式编程算法(gene expression programming，GEP)是融合和遗传算法(GA)和遗传规划(genetic programming，GP)的特点演化而成的算法[12]。

首先，在基因型上(句法上)，基因表达式编程算法继承了GA的定长线性编码的特点，以K-表达式的形式表示[13]。GEP的染色体可以由单个或多个GEP基因组成。GEP的基因是由基因的头部h和尾部t组成，基因的头部既可以包含函数符又可以包含终结符，而基因的尾部只能包含终结符。其中头部的长度是根据具体的问题来决定的，基因尾部的数量由头部数量决定，公式为：

t=h×(n-1)+1

(14)

其中，n表示所需变量数量最多的函数的参数个数(例如在常见的数学运算中，绝对值和三角函数运算n=1，而大多数的算数运算如加减乘除n=2)。GEP采用这种将头部和尾部分开的基因形式，一方面整个基因的结构在设定了函数集合和头部长度之后就能够确定；另一方面，整个基因在该公式的前提下一定能够保证结构上的正确性，而不用担心会产生任何非法的个体。

其次，在表现型上(语义上)，GEP继承了GP的树形结构，称为表达式树。表达式树上的叶节点表示运算数，也就是终结符。分支节点表示运算符，也就是函数符。尽管GEP采用固定长度的基因，但其对应的表达式树形式却千差万别。但无论染色体怎样变异，这些表达式树都是有效的。GEP的基本流程框架如图1所示[14],具体步骤如下:

①设置控制参数,选择函数集合并设置终结符；

②创建初始种群,包含若干个代表不同解答方案的个体；

③解析GEP的基因解码,计算每个个体的适应度值用以评价种群；

④若达到设定最大进化代数或计算精度,则进化结束,否则执行步骤⑤；

⑤根据“适者生存”原则，实施最优化保存策略；

⑥遗传操作产生下一代：分别利用选择、变异、倒串、插串(包括IS插串、RIS插串、基因插串)、重组(包括单点重组、两点重组、基因重组)、随机变量变异对群体实施遗传操作；

⑦生成新种群，并计算各个个体的适应度函数值，然后返回步骤④。

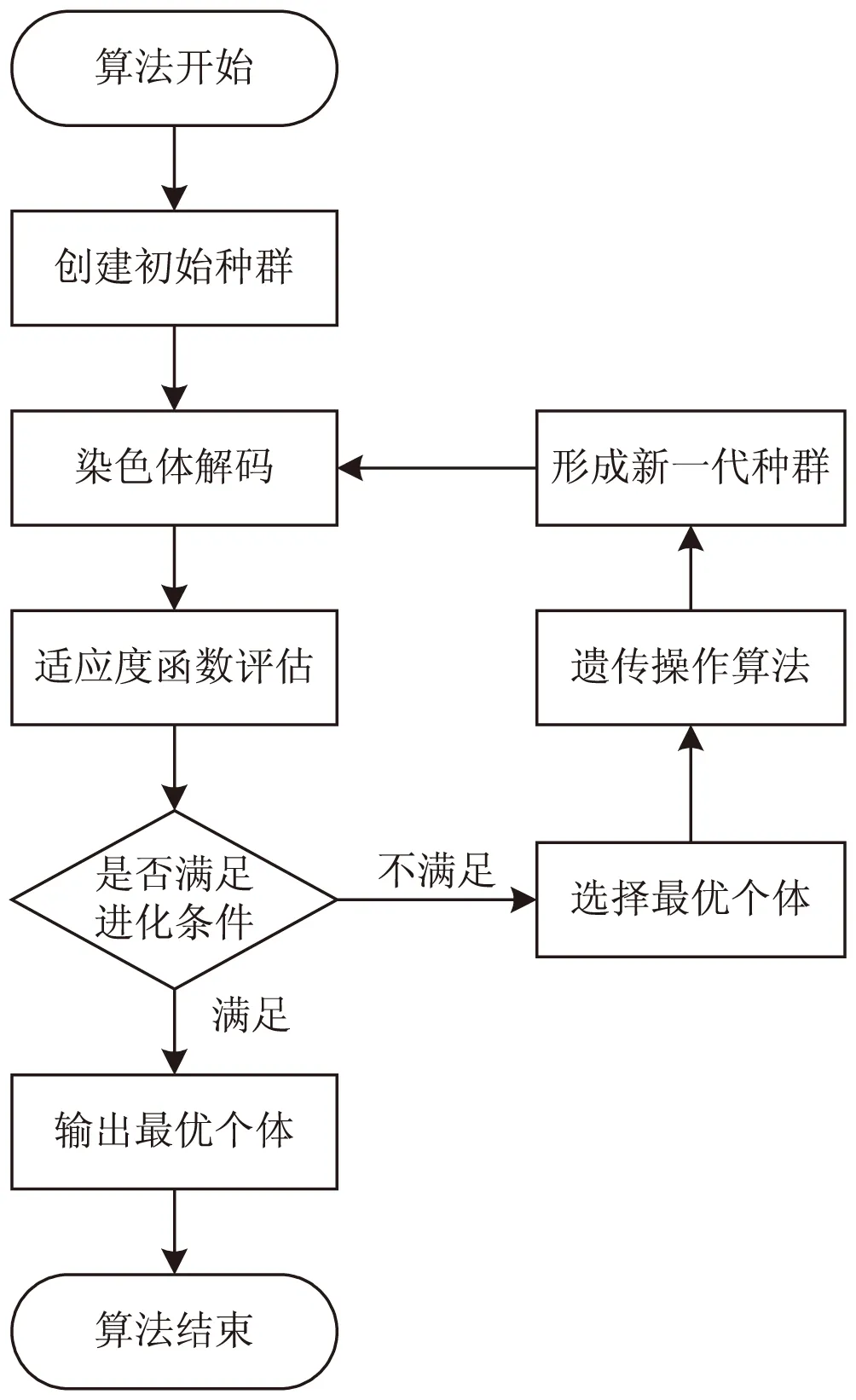
图1 GEP算法流程

3.2 基因表达式编程的适应度函数

基因表达式编程的适应度函数是进化算法与现实问题的接口，同时也是算法演化过程的主要驱动源泉。适当的适应度函数可以评价算法所求得的问题解的优劣。适应度函数的计算一般按照以下步骤进行：

①对个体的编码串解码，得到个体的表现型；

②由个体的表现型计算出相应个体的目标函数值；

③依据最优化问题的类型，由目标函数值按照一定的转换规则求出个体的适应度函数。

通过上述组卷问题的数学模型可以得到组卷问题关于基因表达式编程算法的适应度函数为：

W=1 000-(N+Q+M+P)

(15)

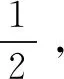
(16)

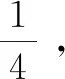
(17)

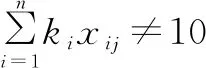
(18)

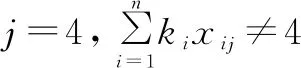
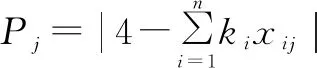
(19)

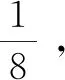
(20)

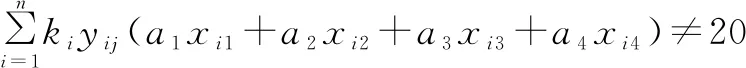
(21)

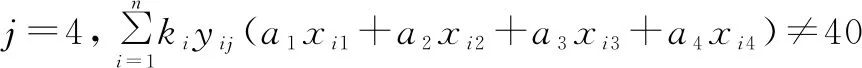
(22)

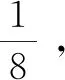
(23)

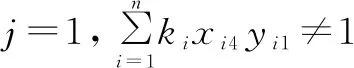
(24)

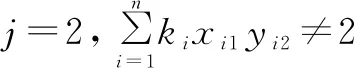
(25)

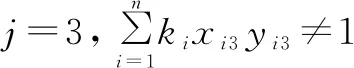
(26)

3.3 基因表达式编程的遗传算子

GEP采用的是线性等长的编码方式，所以基因表达式编程的遗传操作类似于遗传算法[15]。GEP在进行各种遗传操作时满足“保持基因的长度不变，尾部只能出现终结符”的原则，因此，经过遗传操作后的子代染色体仍然是合法的。GEP区别于遗传编程的一个特点是：GEP的一个染色体可以多次进行不同的遗传操作，也可以不进行任何的遗传操作。

GEP的遗传算子包括：选择、变异、倒串、插串(包括IS插串、RIS插串、基因插串)、重组(包括单点重组、两点重组、基因重组)等算子[16]。对于组卷算法，只可用到变异和重组(单点重组、两点重组)。

①变异。

在GEP中，变异是维持种群多样性的主要方法，变异可以发生在染色体上的任何位置，染色体的变异过程如图2所示，3-8位为尾部，变异位置用下划线表示：

图2 GEP染色体变异过程

②重组。

重组包括了单点重组、两点重组和基因重组[17]。单点重组，顾名思义是在组卷染色体中寻找到两个父代染色体，然后在两个父代染色体中随机选取一个交换位置，然后互相交换交换位置后面的染色体部分，从而形成两个新的子代染色体。染色体的单点重组过程如图3所示，3-8位为尾部，重组部分用下划线表示。

图3 GEP染色体单点重组过程

图3中选择父代1与父代2的4号基因位置为交换点，子代1是父代1交换父代2中的部分得到的，子代2是父代2交换父代1中的部分得到的。

两点重组就是首先寻找到两个组卷父代染色体，然后在两个染色体上随机选择两个交换位置，然后互相交换两个位置间的部分，以达到产生两个新的子代染色体的目的。染色体的两点重组过程如图4所示，3-8位为尾部，重组部分用下划线表示。

图4中子代1、子代2是父代1、父代2以2号位置和4号位置为重组点交换中间部分得到的。

4 仿真结果与分析

文中构造了一个题目总数为1 000道题的题库进行实验，其中1～300题为选择题，301～600题为填空题，601～800题为判断题，801～1 000题为大题。

图4 GEP染色体两点重组过程

实验环境为：Windows7操作系统，CPU为i5-4210 M，内存为4 G，使用python3.7编程实现。

程序中变异、单点重组、两点重组的概率为P=(0.28,0.41,0.31)，则实验使用参数如表2所示。适应度函数越接近1 000则得到的结果越好，当适应度函数为1 000时，达到最佳组卷效果。

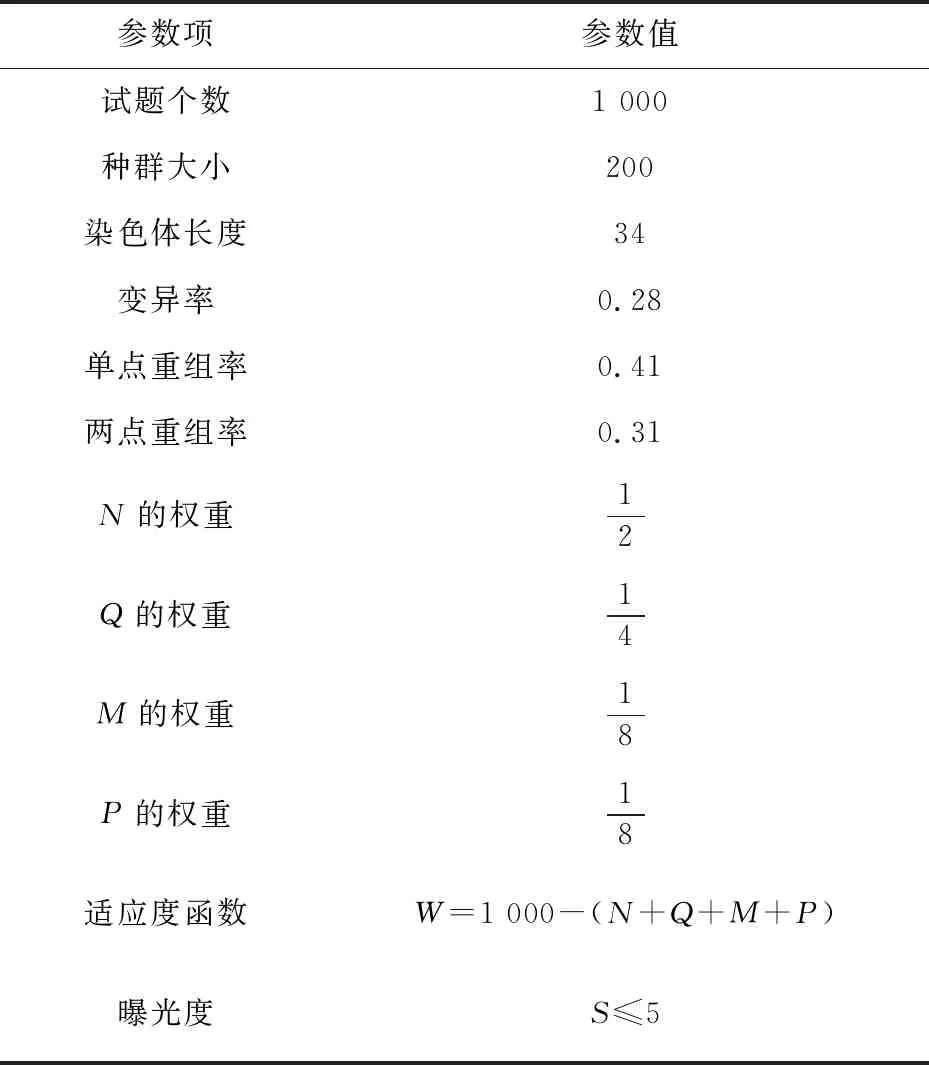
表2 进化中使用的参数

迭代次数与适应度函数的变化如图5所示。通过图5可以看出，由于初始化种群时得到的种群比较理想，故开始时最佳适应度函数就已经在980～1 000的范围内波动，试卷的平均适应度则在870～950的范围内波动，经过496次迭代后，最佳适应度函数达到1 000，即组卷达到最好效果。

通过试验输出的试卷中的试题在题库中的编号为[538，61，748，683，275，330，50，979，510，774，705，168，945，759，471，589，27，77，835，798，679，454，53，682，663，177，321，158，273，68，691，219，215，806]，也就是说这套试题符合给定的约束条件，该组卷算法成功地完成了组卷任务。

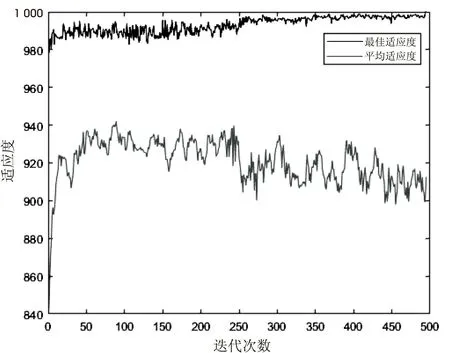
图5 最佳适应度与平均适应度

5 结束语

通过试验验证，基于基因表达式编程算法的智能组卷算法在给定试卷约束条件的前提下，构建出组卷问题的数学模型及相应的适应度函数，便可以很快地计算得到理想的结果，即满足条件的试卷，能有效地防止“早熟”，且简单快捷，具有较高的实用价值。