平衡悬架精准建模与推杆特性研究

王孝鹏

（1.三明学院机电工程学院，福建 三明 365004；2.机械现代设计制造技术福建省高校工程研究中心，福建 三明 365004）

1 引言

国内商用牵引车与国外同类型车辆设计及执行标准不同，主要体现在国外商用牵引车底盘全部采用拖拽式非独立单驱动桥或者双轴系及多轴系车桥，弹性元件多采用空气弹簧；国内商用货运牵引车，水泥搅拌车，消防车，及特殊工程车辆后悬架多采用推杆式平衡悬架。平衡式悬架物理动力学模型难点主要体现在：（1）板簧精确模型建立，（2）双轴系及多轴系集成参数的建立。文献中平衡悬架模型建模主要采用3种方法：（1）采用弹簧质量系统建立双轴系及多轴系，此模型只考虑悬架的系统的垂向振动特性；（2）在VIEW模块建立平衡悬架模型，此模型为物理动力学悬架模型，与真实的平衡悬架模型贴近，缺点是平衡悬架模型缺少集成参数，只能作为单一的系统部件进行研究，基于VIEW模块商用整车模型建立及匹配复杂程度高；（3）平衡悬架装配体有限元模型，此模型主要对悬架的总刚度、零部件进行分析，并不能较好的考虑悬架的动力学特性；文献[1-2]主要对平衡悬架板簧间的摩擦粗糙问题进行了二次开发并提出了一种动刚度公式定义方法，提升板簧模型的准确性；文献[3-5]采用弹簧质量模型建立牵引车及挂车的数模并采用MATLAB计算模型的垂向特性，文献并没有系统考虑平衡悬架的侧向特性及物理结构因素；文献[6-10]采用有限元法对装配体平衡悬架对称模型进行模态分析，从疲劳和耐久特性角度找出平衡悬架系统及零部件损伤与破换的原因；针对此问题，提出CAR模块中通过编写白驱动轴状态参数程序，采用与钢板弹簧模型合并特性可以把驱动轴悬架模型任意拓展的N轴系，用此种方法建立的平衡悬架可以快速与组装整车并与其他子系统进行匹配，在整车架构下研究平衡悬架推杆结构特性变化对整车稳定性的影响。

2 平衡悬架模型

平衡悬架建模的核心是钢板弹簧模型与悬架集成参数，双轴及多轴模型参数需要采用通用模块合并功能实现，Car模块并不支持多轴集成参数；钢板弹簧采用非线性梁建模，完成平衡悬架模型建立，如图1所示。平衡悬架共包含476个自由度。

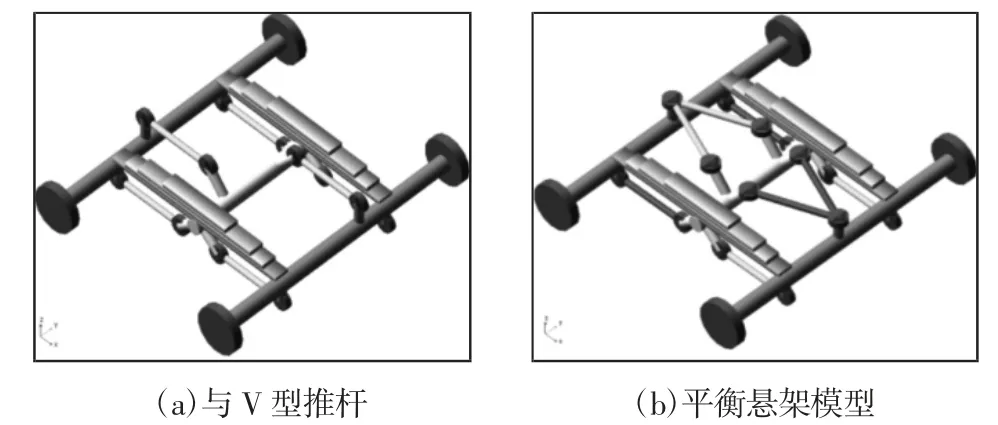
图1 平行式推杆Fig.1 Parallel Push Rod

2.1 白双驱动轴程序

白双驱动轴指驱动轴模型仅包含描述动力传递的方程及车辆定位主销参数等，并不考虑其物理结构。平衡悬架的双驱动轴参数需要通过单驱动轴合并功能实现，单驱动轴状态参数程序如下：

图2 白双驱动轴模型Fig.2 White Double Drive Shaft Model

左半轴转速程序：halfshaft_omega_left：1004.0，（._my_bus_drive_axle.gel_hub.jxl_joint_i_7.adams_id），（._my_bus_drive_axle.gel_drive_axle.jxl_joint_j_7.adams_id），（._my_bus_drive_axle.gel_drive_axle.jxl_joint_j_7.adams_id），（._my_bus_drive_axle.cil_tire_force_adams_id）；

右半轴转速程序：halfshaft_omega_right：1004.0，（._my_bus_drive_axle.ger_hub.jxr_joint_i_7.adams_id），（._my_bus_drive_axle.ger_drive_axle.jxr_joint_j_7.adams_id），（._my_bus_drive_axle.ger_drive_axle.jxr_joint_j_7.adams_id），（._my_bus_drive_axle.cir_tire_force_adams_id）；

左右半轴转速差程序：delta_halfshaft_omega：（varval（._my_bus_drive_axle.halfshaft_omega_left）-varval（._my_bus_drive_axle.halfshaft_omega_right））*9.5493；

差速器力矩程序：differential_torque：sign（AKISPL（ABS（varval（._my_bus_drive_axle.delta_halfshaft_omega）），0，._my_bus_drive_axle.gss_differential），varval（._my_bus_drive_axle.delta_halfshaft_omega））。

白双驱动轴通过两个单轴系驱动轴合并建立，合并过程包含单驱动轴程序，合并完成后白双驱动轴模型，如图2所示。

2.2 钢板弹簧模型

采用Beam梁建立4片装配体钢板弹簧对称模型，如图3所示。板簧对应Beam块之间采用接触属性模拟簧片之间的摩擦特性，点面副约束限制Beam块的之间的运动方向，起到弹簧夹的作用。板簧在X方向对称中心的上下Beam块之间采用3个固定副约束，此固定副起到板簧无效长度作用，即板簧通过骑马螺栓与车轴固定后，骑马螺栓固定长度范围对板簧的刚度并没有影响。Beam块的参数为30×100，单位：mm。

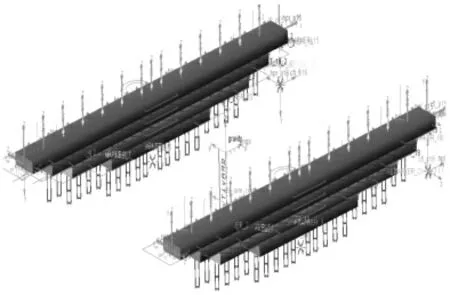
图3 对称板簧模型Fig.3 Symmetrical Leaf Spring Model

2.3 刚度仿真

2.3.1 振动台架模型

构建平衡悬架刚度仿真测试台架，如图4所示。在轮毂处建立四个刚性轮胎，轮胎与轮毂采用固定副约束；修改轮毂与白驱动轴之间的旋转约束副为固定约束副；四个垂向振动试验台与大地采用移动副约束；刚性轮胎与振动台采用点面虚约束，此约束副的主要作用是保证刚性轮胎在振动台架的平面上进行移动。

图4 平衡悬架刚度实验台架Fig.4 Balance Suspension Stiffness Test Bench

2.3.2 垂向刚度测试

图5 平衡悬架垂向刚度Fig.5 Balanced Suspension Vertical Stiffness

A振动台与B振动台在移动副上分别施加驱动位移函数：50.0*SIN（180d*time），运行仿真时间1s，A、B试验台垂向运动50mm后返回初始位置，经计算平衡悬架垂向总刚度，如图5所示。平衡悬架垂向刚度曲线为闭合非重合曲线，由于板簧前端与白车轴之间的移动副存在间隙，接触瞬间产生撞击导致力较大，接触间隙抵消后板簧力回复到整车状态。

2.3.3 扭转刚度测试

平衡悬架在经过坑洼路面时整车车桥会产生扭转刚度，测试时，A振动台施加驱动位移函数：50.0*SIN（180d*time），其余三个实验振动台放空保持静止，运行仿真时间1s，经计算平衡悬架扭转刚度，如图6所示。扭转刚度曲线同为闭合非重合曲线。

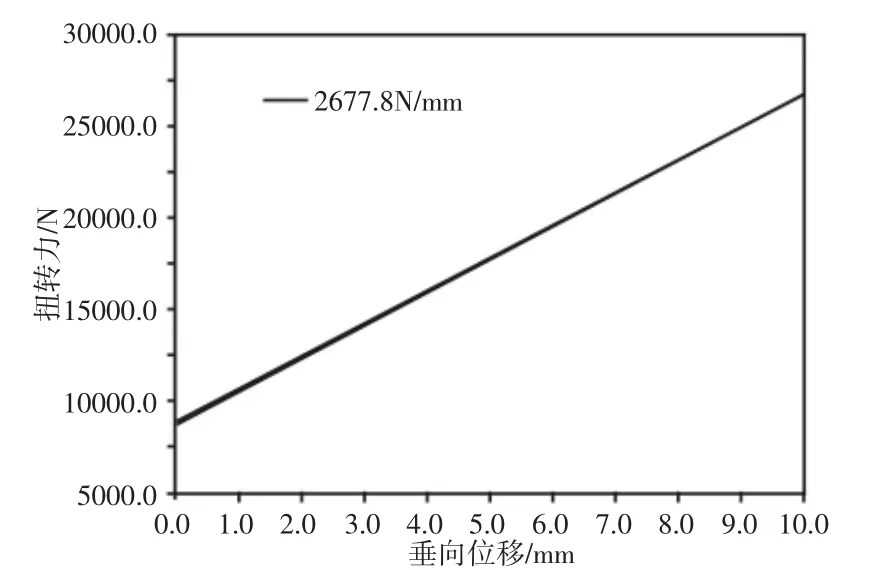
图6 平衡悬架扭转刚度Fig.6 Balance Suspension Torsional Stiffness

3 推杆传力模型

图7 动力传动路线Fig.7 Power Transmission Route

推杆开口角度大小会影响到平衡悬架的侧向力，侧向力大小是影响整车稳定性最关键的参数；整车动力传动路径，如图7所示。由传动轴同时驱动前后驱动桥，前后驱动桥通过推杆与车架连接处B、C、B′、C′点传递纵向驱动力带动整车行驶。推杆受力模型，如图8所示。

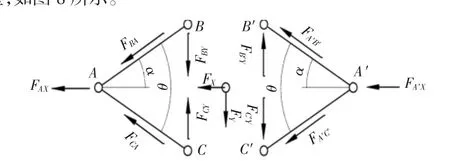
图8 推杆受力模型Fig.8 Pusher Force Model

推杆受力公式如下：

式（2）～式（7）带入到式（1）中整理得：

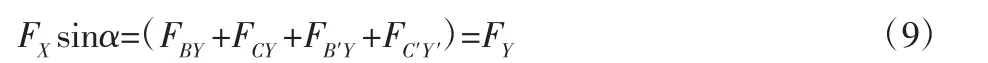
式中：FX—X方向驱动力；FY—平衡悬架平衡力；FAX—连接A点X方向驱动力；FA′X—连接A′点X方向驱动力；FBA—前推力杆BA方向传递力；FCA—前推力杆CA方向传递力；FA′B′—后推力杆A′B′方向传递力；FA′C′—后推力杆A′C′方向传递力；FBY—连接B点Y方向驱动力；FCY—连接C点Y方向驱动力；FB′Y—连接B′点Y方向驱动力；FC′Y—连接C′点Y方向驱动力；θ—推杆夹角；

式（4）与式（5）为前推杆在Y方向上的平衡力，大小相等，方向相反；式（6）与式（7）为后推杆在Y方向上的平衡力，大小相等，方向相反；式（9）中可以看出，随着推杆夹角θ增加，推杆侧向平衡力FY增加，即驱动力FX通过平衡悬架推杆平衡抵消掉的力增加，因而传递车架上的力减少，整车稳定性提升。

4 稳定性仿真

考虑三种V型推杆安装方式：（1）V型推杆角度为17.4°，此时V型推杆开口与中轴中心部位连接；（2）V型推杆角度为35.2°，此时V型推杆开口与中轴左右侧中心部位连接；（3）V型推杆角度为49.6°，此时V型推杆开口与车架连接；车架宽度限制V型推杆开口的最大角度。为检验推杆对平衡悬架的稳定特性的影响，需要整车在特殊路面下进行极限工况测试。构造连续减速带路面模型，如图9所示。路面包含3个等间距分别为10m的减速带，路面宽度为12m，路面摩擦系数为0.9，减速带断面宽度为0.35m，高度为0.05m。整车模型的难点是平衡悬架模型模型建立及系统之间的匹配，构建6×4整车模型，如图10所示。整车模型包含后平衡悬架，前转向桥，右舵转向系统，发动机，简化刚性车型，盘式制动系统，前后轮胎模型，整车模型包含841个自由度。整车在制动过程中通过减速度，更能检验平衡悬架的稳定特性，同时更能体现不同推杆位置与角度对稳定性的影响。整车制动参数设置如下：初始制动速度为50km/h，制动开始时间为第4s，制动减速度设置为0.6g，制动过程中方向盘角度锁定，制动过程为闭环控制。制动过程中整车过减速，如图10所示。

图9 连续减速带路面模型Fig.9 Continuous Deceleration Belt Pavement Model

图10 6×4整车模型Fig.10 6×4 Vehicle Model

计算结果，如图11～图14所示。图中：B1—基于平行式推杆式平衡悬架整车参数变化曲线，B2—基于V型推杆（35.2°）式平衡悬架整车参数模式下变化曲线。侧向加速度B1的RMS值为33.61，幅值最大绝对值为307.72；B2的RMS值为8.69，幅值最大绝对值为60.74，有效值RMS提升74.14%，最大震荡幅值改善80.26%；侧倾角速度B1的RMS值为0.33，幅值最大绝对值为2.92；B2的RMS值为0.16，幅值最大绝对值为0.87，有效值RMS提升51.52%，最大震荡幅值改善70.21%；俯仰角速度B1的RMS值为5.37，幅值最大绝对值为20.50；B2的RMS值为4.91，幅值最大绝对值为17.92，有效值RMS提升8.57%，最大震荡幅值改善12.59%；横摆角速度B1的RMS值为0.081，幅值最大绝对值为0.57；B2的RMS值为0.037，幅值最大绝对值为0.14，有效值RMS提升54.32%，最大震荡幅值改善75.44%。当V型推杆角度为17.4°与49.6°时，整车稳定性参数，如表1所示。从表中数据可以看出，随着推杆角度的增加整车稳定参数指标都明显的提升。

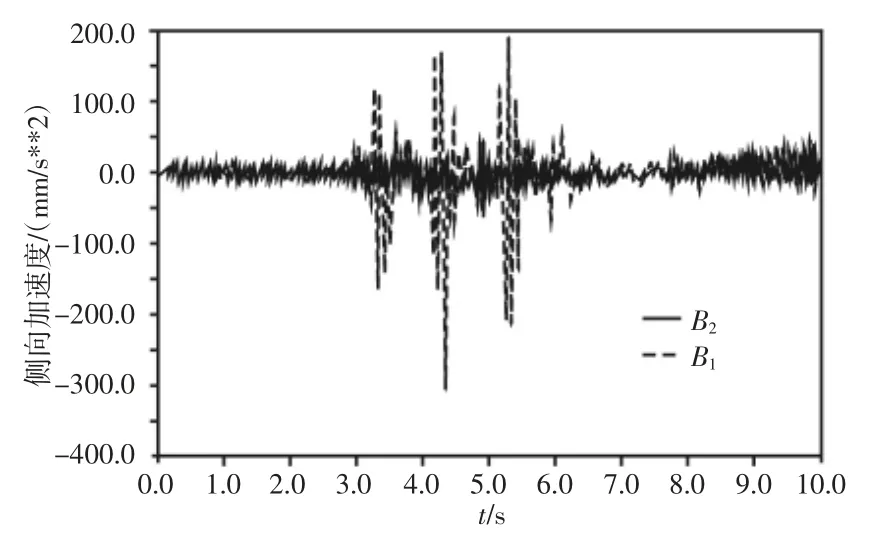
图11 侧向加速度/（平行式、V型）Fig.11 Lateral Acceleration/（Parallel，V-shaped）

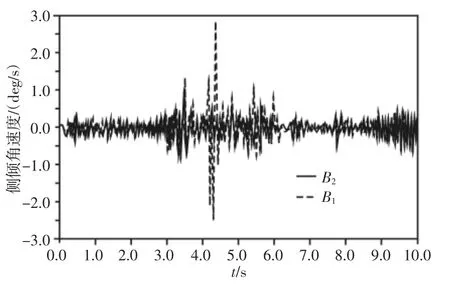
图12 侧倾角速度/（平行式、V型）Fig.12 Roll Angular Velocity/（Parallel，V-shaped）

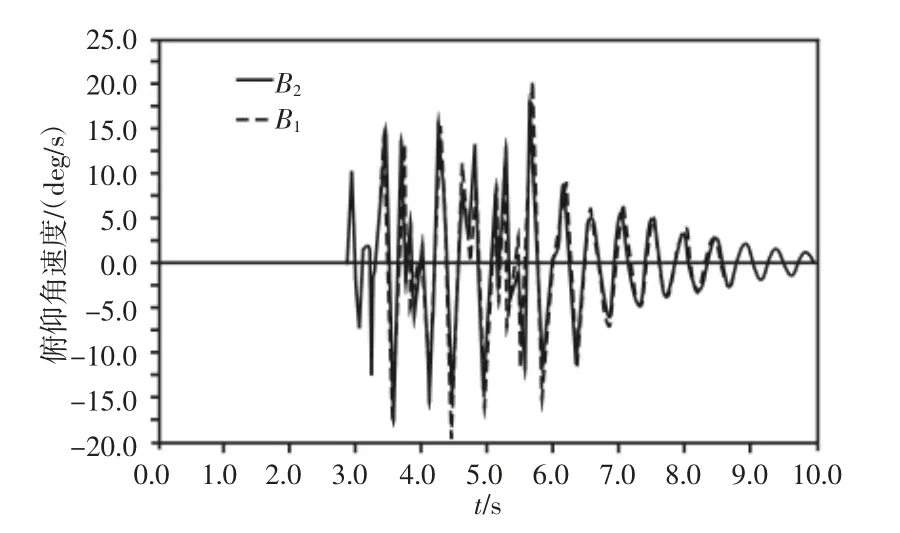
图13 俯仰角速度/（平行式、V型）Fig.13 Pitch Angular Velocity/（Parallel，V-shaped）

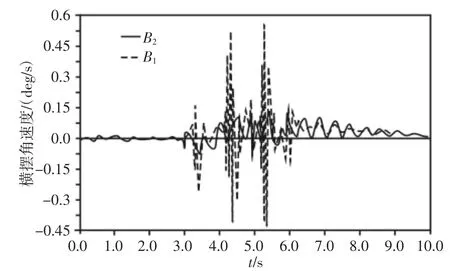
图14 横摆角速度/（平行式、V型）Fig.14 Yaw Angular Velocity/（Parallel，V-shaped）

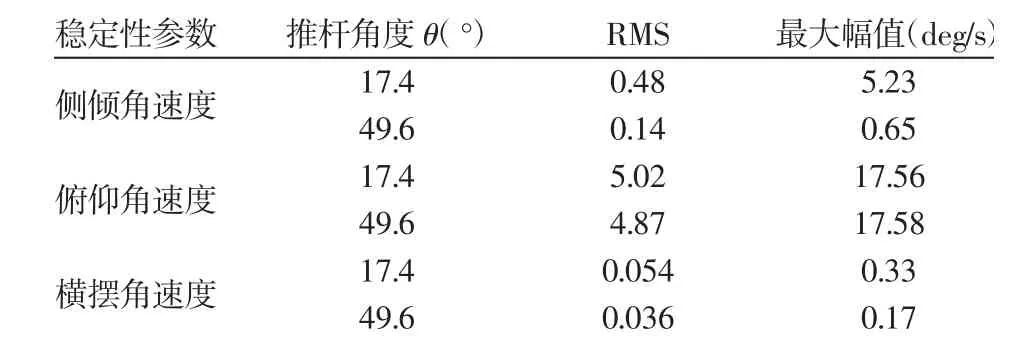
表1 稳定性指标参数Tab.1 Stability Indicator Parameters

5 总结

（1）通过编写白驱动轴状态参数程序及BEAM梁法建立平行杆式与V型推杆式平衡悬架精准模型，振动台架仿真计算出平衡悬架总垂向刚度与弯曲刚度分别为5515.2N/mm、2677.8N/mm；（2）推杆传力模型表明随着V型推杆开口角度的增加，推杆Y方向抵消平衡力增加，通过推杆传递到车身上的侧向力减少，稳定性提升；（3）整车连续减速带制动仿真表明：相对于平行推杆式平衡悬架，V型推杆式平衡悬架在提升整车稳定性方面优势明显，且随着V型推杆开口角度增加，稳定性能持续提升，同时验证了推力杆模型的正确性；（4）平衡悬架模型对于商用整车模型建立及系统分析具有理论与工程上的指导意义。